基于扩展基本时段法的随机回收率ELSPR

舒曼莉，徐克林，郑永前

同济大学 机械与能源工程学院，上海 201804

基于扩展基本时段法的随机回收率ELSPR

舒曼莉，徐克林，郑永前

同济大学 机械与能源工程学院，上海 201804

1 引言

再制造中的丰厚利润，让许多制造企业纷纷进入再制造市场。再制造市场上的产品，一些再造品价值低于制造新品，比如汽车发动机、复印机等；另一些再造品，例如一次性相机、托盘、集装箱等的再造品与制造新品有相同价值。合理调度产品生产顺序和批量成为有效减少总生产成本的关键，即经济批量调度问题，Hsu证明经济批量调度问题是NP-Hard问题[1]。在考虑再造的经济批量调度中，需同时调度制造和再造批量以满足需求，并考虑两种库存成本，问题更复杂，求解可行域更小。针对再造品和制造新品有同等价值的情况，如何调度产品生产批量，包括制造批量和再造批量，从而减少总成本这一问题成为研究热点。

经济批量调度问题最初由Rogers提出，其研究调度产品生产顺序和批量以使成本最低[2]。Davis提出混合整数规划方法求解，可得最优解，但随问题规模的扩大，求解时间激增[3]。Raza和Akgunduz基于批量变动法利用模拟退火方法求解，大幅度缩短求解时间，但随问题规模扩大，所得解与最优解误差增加[4]。Zanoni等采用基本时段法求解，其优化结果较之前研究更优，计算时间比文献[3]大幅降低，但该算法不能保证所得解可行[5]。结合实际生产情况，Tang和Teunter首次研究考虑旧产品回收的经济批量调度问题（Economic Lot Scheduling Problem with Returns，ELSPR），并提出复杂算法求解，结果表明其方法能有效减少成本[6]。文献[7]在两条生产线上分别进行制造和再造的情况，虽多启用一条生产线，但总成本减少量足以抵消新开生产线的成本增加量。由于ESLPR的混合整数规划求解方法过于复杂，基于公共周期法，Teunter提出启发式算法求解，能有效降低部分总成本，但该方法仅对产品生产率小于50%的情况适用[8]。Feng基于公共周期法建模，假设产品的制造次数和再造次数之比为M/R，M和R不同为1，提出启发式算法求解，其假设更接近实际，但所提算法过于复杂，难以推广[9]。以上研究虽考虑问题时更结合实际，但求解方法仍不理想，或无法求得最优解，或所得解不可行。因此，目前的研究仍延续贴合实际的趋势，找寻较优求解方法以快速求得最优并可行的解。

ELSPR求解方法有：公共周期法、基本时段法和批量变动法。公共周期法限定产品生产周期均相同，只要存在可行调度，该方法一定能得到可行解，简单易行，但所得解通常较最优解误差大。批量变动法假设产品可在一个周期内生产多次，但不易求解同时考虑制造和再造批次的ELSPR。除文献[5]外，研究者均采用公共周期法，虽简单易行，但优化效果差，故本文采用扩展基本时段法（Extended Basic Period Approach，EBP）。该方法放宽了对周期的限制，所得解优于公共周期法，但其难以保证收敛到可行解。不可行解出现的原因：一是超出能力限制，即基本时段内需生产产品超出设备生产能力；二是排序不当造成产品生产时间冲突，即同一时刻需设备生产两个或以上产品。本文提出启发式遗传算法，避免由生产时间冲突造成的不可行解，对超出能力限制所得不可行解赋予惩罚函数，让其受遗传压力被淘汰，在得到可行解的前提下将问题收敛到最优解。

针对现实企业的生产特点（由于生产能力的限制和降低库存成本等原因，会售出部分旧产品以立刻获取利润），本文假设回收旧产品都可能存在一定的处置率，即立刻卖出旧产品获取相应利润。同时，为更符合实际，将旧产品回收率设为随机，建立基于扩展基本时段法和随机回收率的经济批量调度模型，为避免扩展基本时段法造成的不可行解，提出启发式遗传算法，使得求解过程更为快速，并保证所得解可行。

2 基于EBP和随机回收率的ELSPR

2.1 随机回收率的ELSPR问题描述

考虑旧产品回收的经济批量调度问题描述为：单一设备或者生产线可制造/再造N种产品，每种产品的制造/再造速度和需求速度Di已知；设备在任一时刻只能生产一个产品，转换为制造/再造另一种产品时花费一定换模成本和时间；产品的制造/再造单位成本和生产型产品/旧产品库存费率均已知；旧产品回收率βi随机；旧产品的处置费用Vd已知，旧产品处置是卖出获利，Vd小于零；假定计划期连续、无限，如何调度旧产品再造率αi和产品制造/再造时刻，使得使得生产周期Ti内单位总成本最小。

图1表示存在旧产品回收的混合生产系统结构。其中，旧产品库存存放回收旧产品，生产型产品库存存放制造新品和再造产品。其余假设如下：

（1）旧产品回收速度βi服从参数为λi的指数分布；

（3）产品在各自生产周期内只制造和再造各一次；

（4）再造产品和制造新品均能用于满足需求；

（5）生产过程中不允许缺货；

（6）旧产品有一定再造率αi，未再造旧产品被售出。

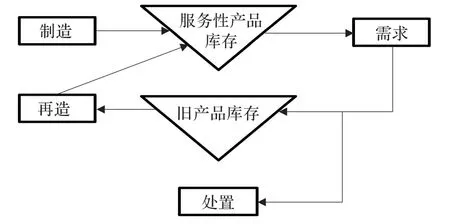
图1 制造/再造混合系统结构图

2.2 基于EBP和随机回收率ELSPR的模型

扩展基本时段法假设每种产品有各自生产周期，产品i生产周期Ti是某基本时段B的2的幂次方倍（PoT策略，Power of Two），即Ti=kiB，ki为乘子。总生产周期Ttoatal即所有Ti的最小公倍数，Ttoatal=kmaxB。PoT策略使得求解过程更容易得到可行解，Maxwell和Singh证明使用PoT策略，求解结果误差不超过6%[10]。

理想情况下，即生产型库存为0时，系统开始制造/再造。此时，理想单位总成本IC包括换模成本Cs、生产（制造/再造）成本Cp、旧产品处置成本Cd、旧产品库存成本Chr，以及生产型产品库存成本Chs：

上述模型中，式（2）表示Ti内单位换膜成本，包括制造和再造换膜成本；式（3）表示Ti内单位生产成本，其中Diαiβi和Di(1-αiβi)分别表示产品i在Ti内单位再造和制造量；式（4）表示Ti内单位处置成本，βi(1-αi)Di表示Ti内单位处置旧产品量；式（5）表示Ti内旧产品单位库存成本，αiβiDi和-αiβiDi分别表示(0～t1)，(t1～Ti)中产品库存增长率，表示旧产品库存量，如图2中阴影部分所示，其中f(βi)为旧产品回收率βi服从分布函数；式（6）表示Ti内生

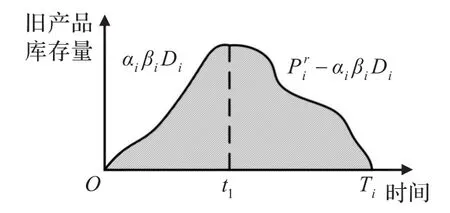
图2 旧产品库存量

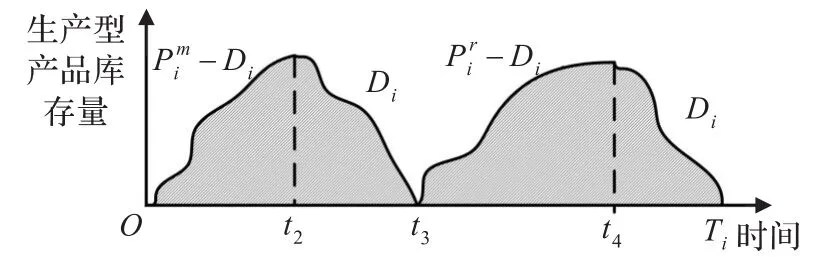
图3 生产型产品库存量

实际生产中，存在非理想情况，即生产型库存不为0时系统开始制造/再造，产生额外成本：

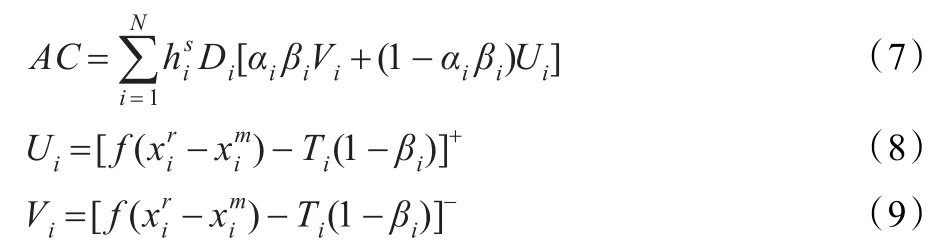
式（7）表示两种非理性情况下的额外成本，如图4、5所示，图中阴影部分表示额外成本。式（8）、（9）中表 f(x)有：有：[z]+=max{z，0}， [z]-=max{-z，0}。示产品i的实际制造时间，Ti(1-βi)表示理想制造时间。对

图4 f(-)＞T(1-βi)条件下额外成本

图5 f(-)＜T(1-βi)条件下额外成本

故目标函数为：

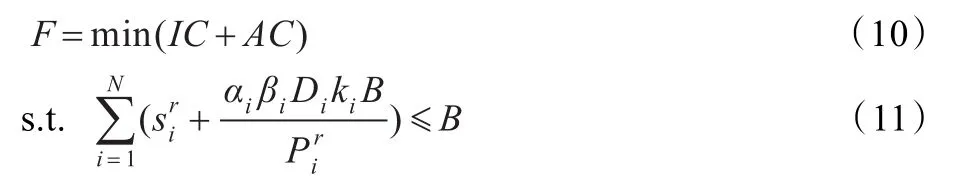
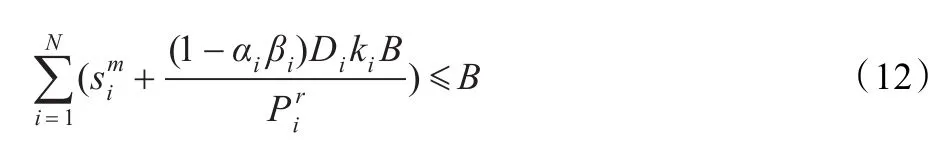
式（11）、（12）为约束条件，保证调度满足设备产能限制，即换模和生产时间之和不超过基本时段。

3 启发式遗传算法

遗传算法（Genetic Algorithm）是模拟达尔文生物进化论自然选择和遗传学机理生物进化过程的计算方法，是一种通过模拟自然进化过程搜索最优解的方法。Fujita首次运用遗传算法求解ELSP，发现该问题适合用遗传算法求解[11]。

实数编码，基因串中分别包含基本时段B，旧产品再造率α，以及乘子k。规模为n的问题，染色体长为2n+1。BUB为该问题用公共周期法所得周期TC，BUB=TC，BLB为该问题用IS（Independent Solution）法求解时所得最小Ti，即BLB=Timin。α由定义可知α∈[0，1]。对乘子k，ki=2ai，ai=0，1， 2，…；=1；根据Hainan Sun[12]可知：

适应度函数，遗传过程中不符合约束（11）、（12）的解赋予惩罚函数而不丢弃，增加种群多样性，避免早熟。fitnessj=Fj+，Fj表示目标函数值，表示相应惩罚函数，t为遗传代数。其中：

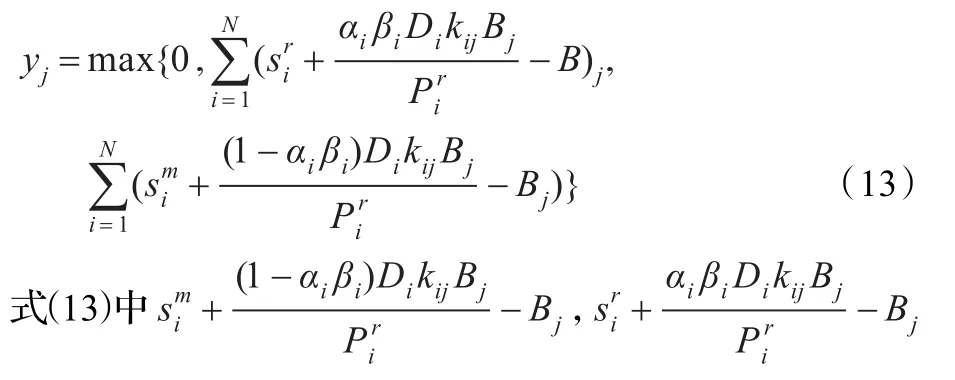
表示制造/再造过程中实际生产时间超过基本时段B的量，将解的不可行程度量化，不可行程度越高，惩罚函数就越大。初始种群，使用启发式规则生成初始种群，避免因生产时间冲突造成的不可行解：

步骤1根据初始种群中的B以及ki，有Ti=kiB；

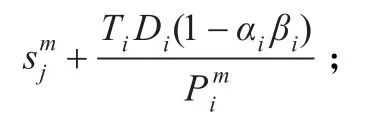
步骤3按-+Ti(1-αiβi)下降顺序，排序所有再造批次，时间间隔

步骤4依次比较再造批次中相邻批次，交换顺序并比较目标函数F是否降低，若降低，则交换两个批次；

步骤5计算末尾再造批次结束时间Tter以及总周期Ttoatal=kmaxB，总松弛时间为Tslack=Ttotal-Tter；

步骤6对满足的产品的再造批次前加入松弛，直至满足-=Ti(1-αiβi)或所有的松弛时间Tslack已分配完。

遗传操作，在“选择复制”中采用轮盘赌结合精英策略，选取父代中适应度函数最小的10%复制得到子代，余下90%子代采用轮盘赌方法在父代中选取。在“交叉”中采用均匀交叉，掩码是随机产生的二进制串。若掩码为1，则子1基因点获取父1的基因信息，子2获取父2的；若掩码为0，则子1获取父2的基因信息，子2则获取父1的，如图6所示。“变异”为多点变异，染色体中每段均给予一定变异几率，变异点随机产生，该基因位上的数值由另一个随机数代替，随机数的产生服从初始种群产生规则。遗传过程中，随遗传代数增加，逐渐降低交叉率，增大变异率，使子代稳定遗传，同时由于变异率增加也保持了种群的多样性。

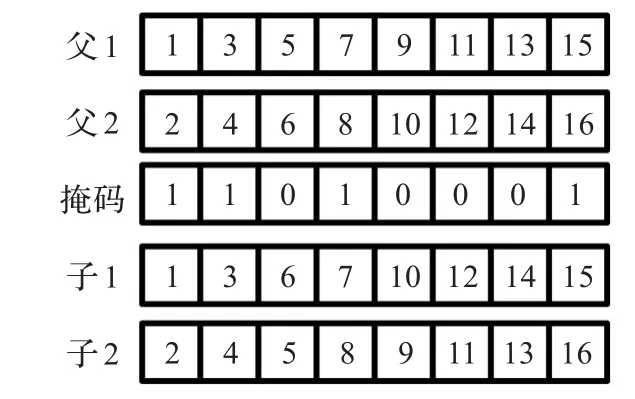
图6 均匀交叉操作范例

终止条件，达到一定代数，或相邻若干代种群平均适应值无变化或变化小于阈值，则退出算法。

4 数值实验

实验数据源于文献[6]，研究对象为一机械部件厂，实例包含5种产品，各产品相关参数如表1所示。通过HGA求解，所得结果如表2、3所示，其中“当前策略”为该机械部件厂当前采用的调度方法。

表2结果表明本文提出的模型对机械厂目前调度有所优化，成本比文献[6]下降3.6%。成本降低集中在额外成本和库存成本。由于目标函数包含产品制造/再造成本，该成本远高于换模及库存成本，且对旧产品再造率αi敏感性小，制造/再造成本变化幅度小，使总成本优化幅度减小。若总成本不包括制造/再造成本，单位总成本较文献[6]所得结果下降18.7%。本文提出的ELSPR求解方法比文献[6]有更好的优化效果。

若不考虑产品处置，即旧产品均可再造，此时制造/再造成本作为定值不包括在目标函数中。优化结果如表3所示，单位总成本比文献[6]所得结果下降17%。虽然优化幅度不大，但建模时考虑旧产品再造率可进一步降低额外成本和库存成本。在建模时考虑旧产品再造率，不仅符合生产实际，而且可以有效地降低成本。

从表1可看出，算例中研究对象生产率均较高，在80%左右。下面对生产率处于中低部分的对象进行研究，实验数据从文献[8]中获得，如表4所示。分别用IS和文献[6]方法及HGA进行求解。IS法求得的解若可行，则其为该问题最优解，但这几乎不可能，尤其对生产率ρ＞0.25的问题[13]。故IS通常作为同类问题的下界。由于IS所得解通常不可行，故不考虑IS法额外成本AC。如表5为三种方法求解结果，由表5可知，在考虑旧产品回收率情况下，HGA所得解比文献[6]下降9.8%。如表6为HGA求解产品调度情况，其中表示产品制造/再造的结束时间，可以看出HGA所得调度可行。在不同的产品生产率下，提出的HGA算法均能取得优于文献[6]的解，并且能保证所得调度的可行性。

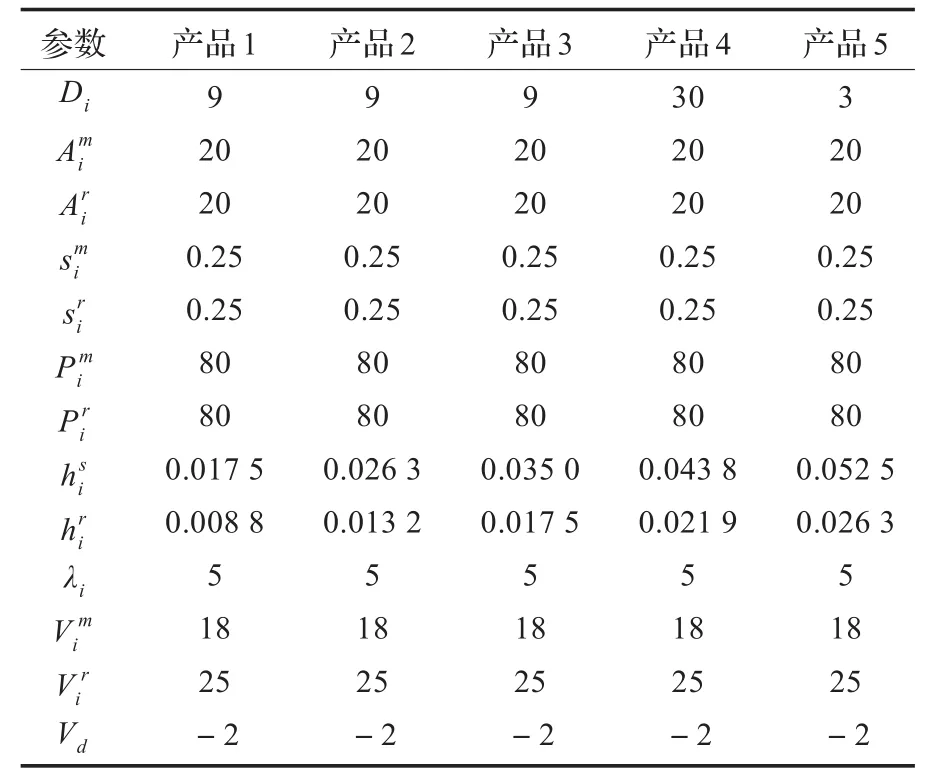
表1 求解模型所用参数

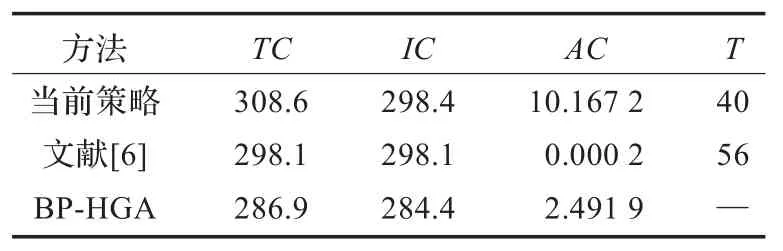
表2 文献[6]和HGA求解结果比较

表3 旧产品均可再造情况下求解结果比较

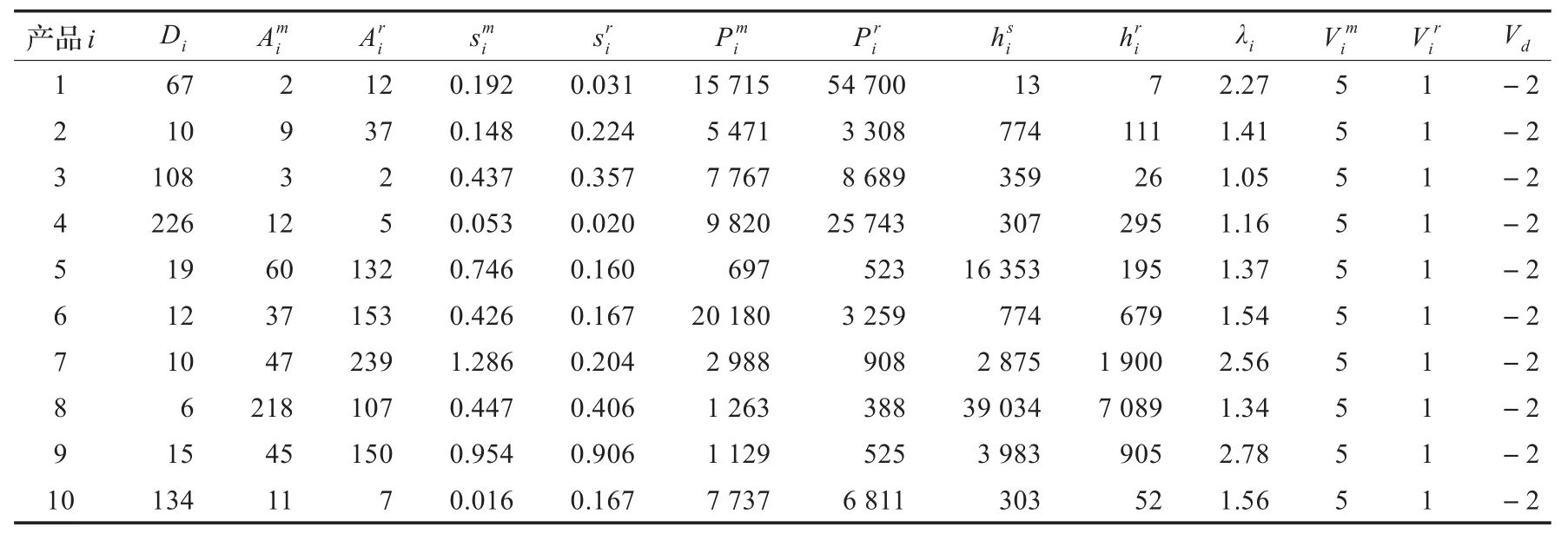
表4 产品相关参数

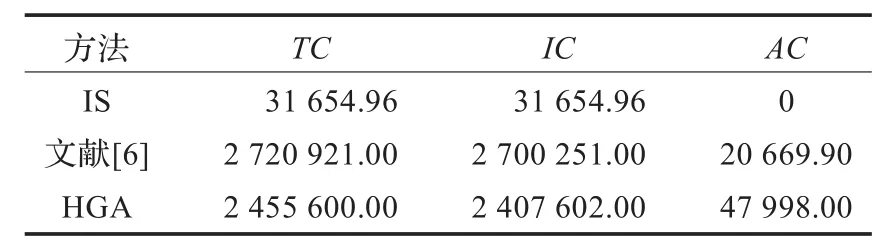
表5 中低生产率下求解结果对比

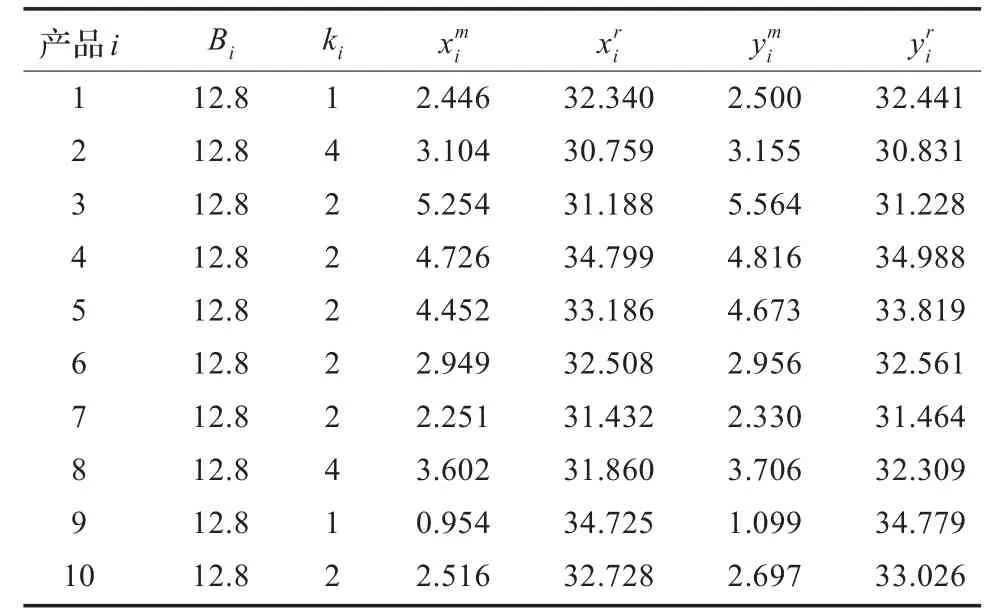
表6 求解模型所得决策变量参数值

5 敏感性分析

对回收率参数λ进行敏感性分析，其余参数如表4所示，结果如图7所示。分析发现，逐渐增大λ值，回收率β均值减小，成本大幅震荡。λ在[0，10]时，成本震荡幅度较大，随着λ逐渐增大，处于[50，100]时，成本逐渐增大。由于生产型库存费率更高，越迟开始再造，库存费用的增加速度减缓。在λ值较大时，系统再造量下降，随着制造批次的增大，总成本增加。λ增大，再造批量减小，制造批量增大，制造单位生产成本高于再造单位生产成本，总生产成本的增加。对λ分析发现，回收率在一定范围内增加可使得成本下降，但是超过该范围后成本反而增加，构建模型是考虑旧产品再造率，使得旧产品不能都用于再造，对于优化ELSPR十分必要。

图7 回收率参数敏感性分析图

6 结束语

针对存在于混合生产系统中的批量调度问题，本文建立了旧产品回收率随机并考虑旧产品处置的ELSPR模型。采用启发式遗传算法结合扩展基本时段法对模型进行求解。实验表明：建模时考虑旧产品回收率，较同等条件下不考虑该参数，能进一步降低总成本达到18.7%；提出的HGA算法在生产率的不同阶段均能求得优于文献[6]的解，并且能保证所得调度的可行性。在将来求解ELSPR时，对初始解的生成采用更优的启发式排序规则，使初始解包含所有可行排序，或对初始解中的不可行解提出修复规则，使初始解尽量多样化，以使得最优解进一步优化。

[1]Hsu W L.On the general feasibility test of scheduling lot sizes for several products on one machine[J].Management Science，1983，29（1）：93-105.

[2]Rogers J.A computational approach to the lot scheduling problem[J]. Management Science，1958，4（3）：264-291.

[3]Davis S G.Scheduling economic lot size production runs[J]. Management Science，1990，36（8），985-998.

[4]Raza A S，Akgunduz A.A comparative study of heuristic algorithms on economic lot scheduling problem[J].Computers and Industrial Engineering，2008，55（1）：94-109.

[5]Zanoni S，Segerstedt A，Tang O，et al.Multi-product economic lot scheduling problem with manufacturing and remanufacturing using a basic period policy[J].Computers and Industrial Engineering，2012，62：1025-1033.

[6]Tang O，Teunter R.Economic lot scheduling problem with returns[J].Production and Operations Management，2006，15（4）：488-497.

[7]Teunter R，Kaparis K，Tang O.Multi-product economic lot scheduling problem with separate production lines for manufacturing and remanufacturing[J].European Journal of Operational Research，2008，191：1241-1253.

[8]Teunter R，Tang O，Kaparis K.Heuristics for the economic lot schedulingproblemwithreturns[J].ProductionEconomics，2009，118：322-330.

[9]Feng Y，Viswanathan S.A new lot-sizing heuristic for manufacturing systems with product recovery[J].Production Economics，2011，133：432-438.

[10]Maxwell W L，Singh H.The effect of restricting cycle times in the economic lot scheduling problem[J].IIE Transactions，1983，15（3）：235-241.

[11]Fujita S.The application of marginal analysis to the economic lot size scheduling problem[J].AIIE Transactions，1978，10：354-361.

[12]Sun H，Huang H C，Jaruphongsa W.A genetic algorithm for the economic lot scheduling problem under the extended basic period and power-of-two policy[J].CIRP Journal of Manufacturing Science and Technology，2009，2：29-34.

[13]Chatfield D C.The economic lot scheduling problem：a pure genetic search approach[J].Computers and Operations Research，2007，34：2865-2881.

SHU Manli,XU Kelin,ZHENG Yongqian

School of Mechanical Engineering,Tongji University,Shanghai 201804,China

For the economic lot scheduling problem of a hybrid production line,the ELSPR considering recycling of old product with stochastic return rate is studied.A model under the extended basic period approach is formulated to get minimum total unit cost,in which manufactured and remanufactured products are simultaneously sequenced.A Heuristic Genetic Algorithm（HGA）is proposed,which can effectively get rid of infeasible solutions caused by schedule intersection and capacity restriction.The solution results of Teunter and HGA are compared whether or not considering disposal.The contrast shows the proposed HGA can further reduce costs and ensure the optimal solution feasible.

economic lot scheduling problem;remanufacturing;returns;disposal

针对存在于制造、再造混合生产系统的批量调度问题，研究旧产品回收率随机的情况下，考虑旧产品回收的多产品经济批量调度问题。基于扩展基本时段法综合考虑制造新品和再造产品的批量调度，构建以单位总成本最小为目标的优化模型。提出的改进型遗传算法对模型求解，能避免不可行解的产生。分别比较考虑和不考虑旧产品废弃处置两种情况下，该算法和Teunter方法的优化效果，结果表明提出的算法能进一步降低成本并保证最优解可行。

经济批量调度问题；再制造；产品回收；废弃处置

A

TP278

10.3778/j.issn.1002-8331.1301-0139

SHU Manli,XU Kelin,ZHENG Yongqian.ELSPR with stochastic return rate under the extended basic period approach. Computer Engineering and Applications,2013,49（13）：216-220.

国家自然科学基金（No.61273035，No.71071115）；国家高技术研究发展计划（863）（No.2009AA043000）。

舒曼莉（1988—），女，硕士研究生，主要研究领域为再制造系统库存与调度管理；徐克林（1945—），女，教授，博导，主要研究领域为供应链管理；郑永前（1965—），男，副教授，硕导，主要研究领域为生产系统工程与管理。E-mail：shumanli@163.com

2013-01-14

2013-03-02

1002-8331（2013）13-0216-05