蚁群聚类的欠定盲源分离方法

王放，何选森

湖南大学 信息科学与工程学院，长沙 410082

蚁群聚类的欠定盲源分离方法

王放，何选森

湖南大学 信息科学与工程学院，长沙 410082

1 引言

盲源分离（Blind Source Separation，BSS）是数据分析及信号处理的强有力工具，在许多领域都得到广泛的应用，如生物医学信号处理、数据挖掘、语音信号处理、模式识别以及无线通信等[1-3]。

所谓盲分离，是指在源信号数目、位置、混合过程等先验信息未知的情况下，仅根据传感器信号来估计源信号。其数学模型为：

其中X(t)=[x1(t)，x2(t)，…，xm(t)]T为观测信号向量，A为未知的m×n维混叠矩阵，S(t)=[s1(t)，s2(t)，…，sn(t)]T为源信号向量，N(t)=[n1(t)，n2(t)，…，nm(t)]T为噪声向量。盲分离就是在A和S(t)均未知的情况下，仅由X(t)恢复出S(t)。当观测信号个数m小于源信号个数n时，就称之为欠定盲源分离。

对于欠定盲源分离问题，一般将求解过程分解为估计混叠矩阵A和恢复源信号S(t)两步。第一步主要采取聚类算法估计混叠矩阵，常用的方法有：势函数法[4]、K-均值聚类法[5]、模糊K-均值聚类[6-7]等；第二步主要是利用估计出的混叠矩阵采取线性规划法或最短路径法等来恢复源信号。而在两步法中，估计混叠矩阵最为重要。Bofill等人率先提出应用势函数的方法进行分离，但由于分离过程中参数设置缺乏理论指导，且易受实验者主观影响，其应用范围有限；另一种应用较广泛的是利用K-均值聚类算法估计混叠矩阵，但该方法需事先确定聚类数目，且估计精度有限。

本文针对上述算法的缺陷提出一种估计混叠矩阵的新方法。首先利用稀疏源信号的直线聚类特性，通过标准化将直线聚类转变成致密聚类[8]，再采用蚁群聚类算法进行聚类搜索，根据搜索得到的聚类中心的个数得到源信号的个数，同时估计出混叠矩阵。本文的方法不需要事先确定聚类数目，就能估计出混叠矩阵；同时基于势函数的方法在三路或三路以上观测信号情况下是无法进行估计的，而本文的方法能有效地实现这类情况下的盲源分离。

2 蚁群聚类算法原理

蚂蚁在觅食过程中会在其经过的路径上释放信息素，同时信息素也会随着时间的流逝而挥发。蚂蚁在运动过程中能够感知路径上的信息素及其强度，并倾向于朝着信息素浓度高的方向移动。因此某一路径上经过的蚂蚁越多，在该路径上累积的信息素就越多，后来的蚂蚁也更倾向于选择该路径，整个蚁群的行为表现出信息正反馈现象。如果将数据视为具有不同属性的蚂蚁，聚类中心是蚂蚁所寻找的“食物源”，那么数据聚类过程就可以看做蚂蚁寻找食物源的过程[9-10]。

假设数据对象为X={X|Xi=(xi1,xi2,…,xim),i=1,2,…,N}，设Xi与Xj之间的加权欧氏距离为dij，当蚂蚁从位置i移动到位置j时，计算路径i→j上的信息素τij[11]：

若Xi与Xj之间的加权欧氏距离dij小于或等于某一阀值r，则设定该路径上的信息素为1，代表蚂蚁会经过该路径，否则其信息素为0。同时由于信息素的挥发，在一次搜索周期结束后，路径上的信息素需要进行更新。设τij(t)代表第t次搜索过程中路径i→j上的信息量，则该次搜索结束后信息素更新为[11]：

τij(t+1)=(1-ρ)τij(t)+Δτij（3）

ρ为挥发系数，Δτij为信息素的增量，其值为在该次搜索周期内所有蚂蚁在该路径上释放的信息素的总和。在搜索周期中，蚂蚁根据转移概率进行合并，转移概率[12]为：

其中ηij称为能见度，大小为1/dij，α和β为调节因子，用来控制信息素和能见度的影响，S={Xs|dsj≤r，s=1，2，…，N}为可行路径的集合。从式（4）可见转移概率与能见度成正比，即与欧式距离成反比，也即两数据点间距离越大，合并的概率越小。如果pij(t)大于阀值p0，则Xi与Xj合并成一类，求出各类数据的算术平均值即为各聚类中心。

3 混叠矩阵估计与信源恢复

3.1 观测信号初始化

当源信号为稀疏信号时，混合信号具有线性聚类特性，如果忽略噪声的影响，将式（1）展开为：

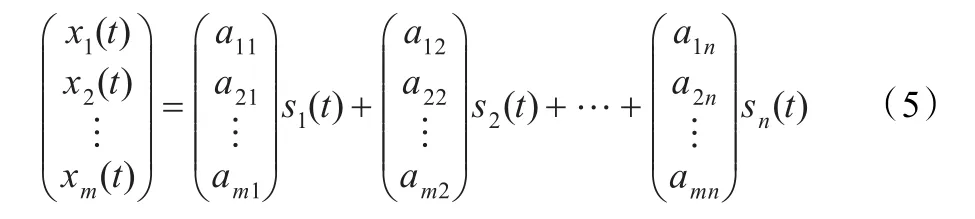
当某一时刻只有一个源信号（如只有si(t)）起作用时，上式可转化为：

它在m维空间中是一条经过原点的直线，直线方向取决于混叠矩阵的第i个列矢量(a1i，a2i，…，ami)T。基于此，n个源信号si(t)，i∈(1，2，…，n)将确定n条直线，因此，A的估计就转化为观测空间中直线方向的估计。采用和文献[4]中相同的语音数据，三路长笛声音源信号经采样后，左乘以随机产生的2×3维混叠矩阵得到两路观测信号，混叠信号散点图如图1所示。

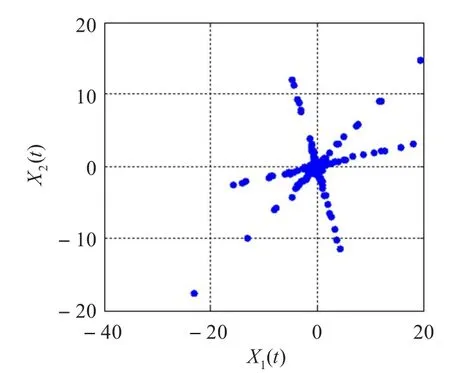
图1 三路源信号混叠散点图

由图1可见，三路源信号确定了三条直线。由于三路源信号比较稀疏，所得散点图上三条直线比较清晰，相互之间重叠干扰部分较少，当源信号不太稀疏时，可以先对源信号进行傅氏变换等使其稀疏化，然后在变换域中进行盲源分离。

3.2 估计混叠矩阵

由于n路源信号经混叠后的散点图表现为经过原点的n条直线，同时各直线的方向对应于混叠矩阵的各列向量。通过聚类算法将观测信号按散点图中各直线所在方向进行分类，每一类对应一条直线，每个聚类中心表示的方向近似散点图中一条直线的方向，即对应混叠矩阵的某个列向量，这样通过聚类就可以获得对混叠矩阵的估计。

本文考虑将直线聚类转变成致密聚类，因此首先对观测信号进行标准化处理包括尺度归一化和方向镜像[13]。对观测信号X(t)的尺度归一化为：

其中‖X(t)‖表示X(t)的Euclid范数。方向镜像就是将下半平面向量映射到上半平面。进行标准化时，由于位于原点附近的数据点存在重叠现象或为噪声点，可去掉这部分数据点，通过去除这部分数据可以有效降低计算量和提高估计精度。经过标准化后的观测信号均位于上半圆周上，如图2所示。

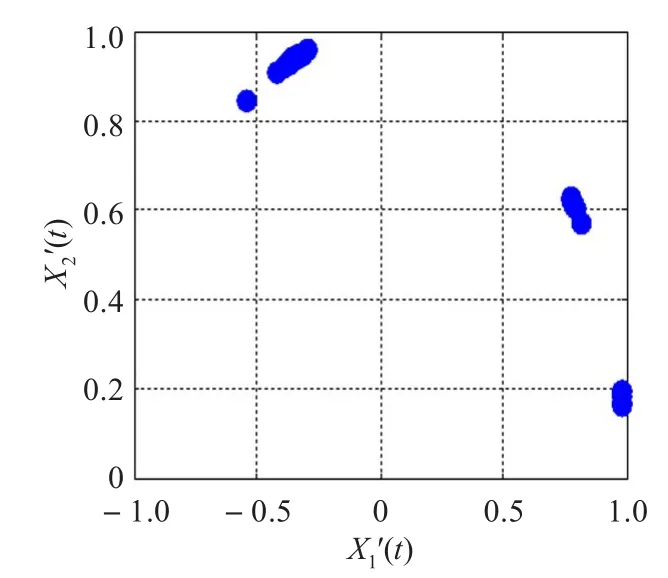
图2 标准化处理后的观测信号

标准化后的观测数据点聚集于单位圆上形成球形簇，酷似蚁群聚集成堆。在每个数据堆中均存在某一数据点所表示的方向最能代表散点图中对应直线的方向。因此获得各数据堆中关键数据点（聚类中心）就能获得对该直线方向的精确估计。故本文提出采用蚁群聚类算法寻找各类中心，确定源信号的个数和混叠矩阵。设标准化后的信号数据点X'(t)=[x1'(t)，x2'(t)，…，xm'(t)]T，t=1，2，…，N，将各数据点看成一只蚂蚁，共有N只蚂蚁，结合蚁群算法进行聚类。首先寻找初始聚类中心，计算各数据点X'(i)和X'(j)之间的加权欧氏距离dij：

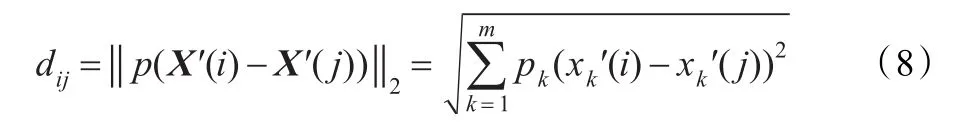
其中m为信号的维数，p和pk为加权因子，因为各维数据影响力一样，故本文中pk均取值为1。利用式（2）计算各路径上的初始信息素τij，这样将得到一个N×N维的初始信息素矩阵，矩阵中每个元素均为0或者1，其中值为1的元素τij代表X'(i)与X'(j)之间的加权欧氏距离dij小于或等于r。因此选择一个适当的r值，只有属于同一类的数据点之间的加权欧式距离才会小于或等于r，对应的τij才等于1。这样属于同一类的数据点，其初始信息素矩阵中所在行的所有元素必都相等。例如：假设X'(1)与X'(a)、X'(b)(a≠b≠1)属于同一类，则除与自身外X'(1)只与X'(a)、X'(b)两个数据点之间的欧式距离d1a、d1b小于等于r，则初始信息素矩阵中第一行所有元素中只有τ11、τ1a、τ1b三个元素为1，其余均为0；对于数据X'(a)，也只与X'(1)、X'(b)两个数据点之间的欧式距离da1、dab小于等于r，所以初始信息素矩阵中第a行中只有τa1、τaa、τab为1，其余也均为0。这样整个初始信息素矩阵中有第1、a、b三行元素相等，即X'(1)、X'(a)、X'(b)属于同一类，再取这三个数据的算术平均值，即得到了第一个初始聚类中心，同理可以得到所有其他初始聚类中心。关于r的选择，如果源信号数目较多，导致单位圆上数据点较密集，可以在第一步的标准化时将数据点归一化到半径大于1的圆周上，这样数据分得较开，r可供选择的范围也较大。寻找到初始聚类中心后进行蚁群搜索，设寻找到的初始聚类中心为C(k)= [x1(k)，x2(k)，…，xm(k)]T，k=1，2，…，K，按式（8）计算各蚂蚁到初始聚类中心的欧式距离，按式（2）计算蚂蚁到各聚类中心路径上的信息素。计算蚂蚁转移到初始聚类中心的概率：如果dij=0，则pij=1，否则根据式（4）计算pij。每只蚂蚁根据计算出来的转移概率进行合并，如果pij大于阀值p0，则X'(i)与该初始聚类中心合并成一类，并根据式（3）更新路径上的信息素；如果pij小于p0，则让其等待下次循环。令CJ={X'(i)|pij＞p0，i=1，2，…，N，j∈(1，2，…，K)}，CJ表示所有归并到C(j)一类的数据集合，则理想聚类中心为：

其中X'(i)∈CJ，J为C(j)类中元素个数。计算各聚类中心的距离，如果距离小于给定的阀值r，则合并相应的两类。重复上述过程直至达到最大迭代次数M，最后得到的聚类中心的个数就代表源信号的个数，每个聚类中心分别代表混叠矩阵的一个列向量，这样就估计出混叠矩阵。

3.3 源信号的恢复

估计出混叠矩阵后，可通过最短路径法进行源信号的恢复。由文献[4]可知，稀疏信号盲分离归结为以下优化问题：

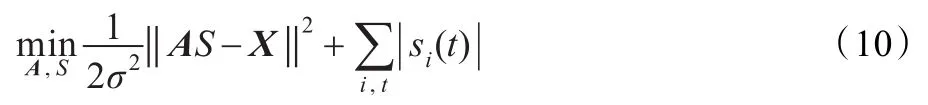
其中σ2为噪声的方差，第一项为重构误差平方和，第二项为非稀疏项。在不考虑噪声的前提下，由于混叠矩阵A已估计出来，则上式等效为：

由上式可知，每个时刻t确定一个优化问题，从而可估计出源信号。

3.4 欠定盲分离算法步骤

通过上述分析，本文的欠定盲分离算法步骤如下。

（1）对观测信号进行标准化处理。

（2）初始化设定r、α、β、p0等参数，将每个数据点看成一只蚂蚁，利用式（8）计算每只蚂蚁到其他数据点间的加权欧氏距离dij，求出初始聚类中心。

（3）计算每只蚂蚁到初始聚类中心的加权欧氏距离。

（4）计算各蚂蚁到初始聚类中心路径上的信息量τij和转移概率pij。

（5）如果pij≥p0成立，则合并蚂蚁到该初始聚类中心，并更新信息素矩阵。

（6）根据式（9）计算各聚类中心Cˉ。

（7）计算各聚类中心间的距离，如果距离小于给定的阀值r，则合并聚类重新计算各聚类中心，否则返回到（3）重新计算。

（8）循环迭代直至最大次数，输出聚类个数和各自聚类中心。

（9）利用求出的聚类中心即对应混叠矩阵A，采用最短路径法恢复源信号。

当存在多路观测信号时，同样可以采用上述算法思想，在多维空间中进行聚类估计。标准化后的观测信号数据点在多维空间中聚集成堆，然后进行蚁群聚类。

4 仿真实验及分析

实验仿真均在Matlab 7.0环境下进行，实验数据采用和文献[4]中相同的语音数据。为了检验对混叠矩阵的估计精度，采用角度偏差进行测算[14]：

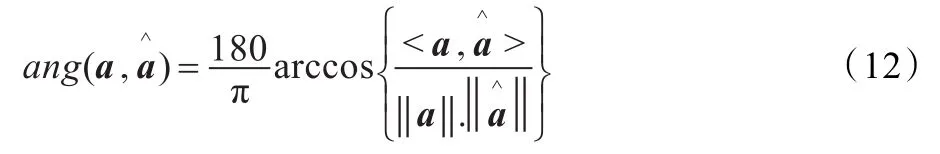
表1 三种方法的a和的角度偏差比较表

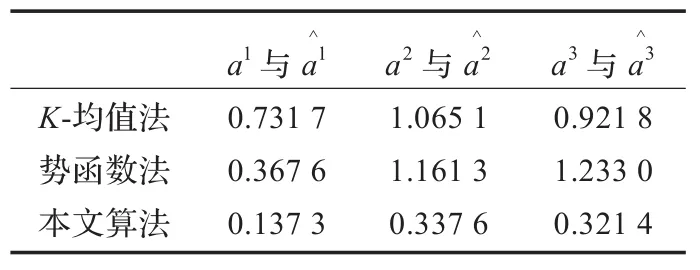
表1 三种方法的a和的角度偏差比较表

a1与a1 ^ a2与a2 ^ a3与a3 ^ K-均值法势函数法本文算法0.731 7 0.367 6 0.137 3 1.065 1 1.161 3 0.337 6 0.921 8 1.233 0 0.321 4

对比实验表明本文算法有更高的估计精度。源信号与恢复后的信号之间的相关系数，如表2所示。

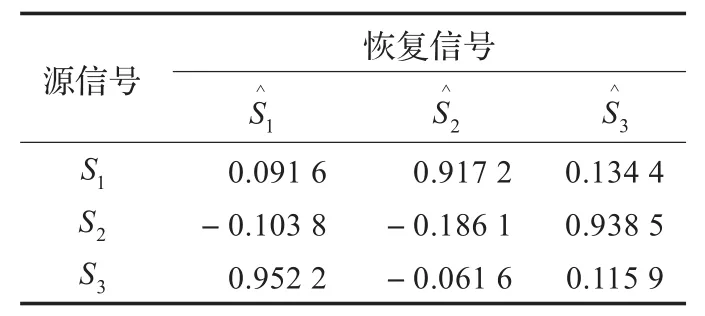
表2 源信号与恢复后信号之间的相关系数表

从表2看出每行每列有且只有一个元素接近1，其余均接近0，说明恢复信号和源信号之间相似度高，应用本文算法估计恢复出源信号效果比较理想。源信号以及恢复后的信号如图3、4所示。

由图看出本文算法能比较精确恢复出源信号。调用Matlab函数wavwrite（）将恢复后的源信号保存成.wav文件。通过试听恢复后的语音信号，本文方法较上文其他两种方法所恢复的信号，语音清晰度得到较好的提高，连贯性得到改善，能清晰分辨出3个长笛声音，试听效果很接近于源信号。

实验2 m=3，n=4，即三路观测信号，四路源信号的情况。随机产生混叠矩阵：

信号散点图以及归一化处理后，见图5、6。

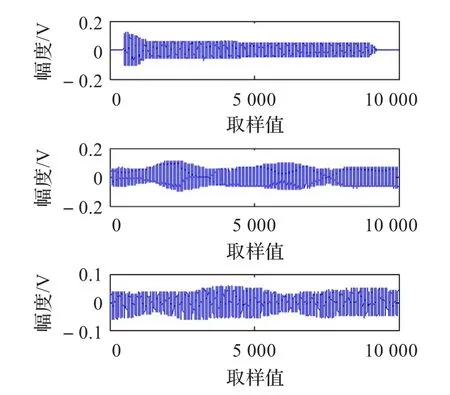
图3 三路源信号

图4 三路恢复信号

图5 四路源信号三路观测信号散点图

同实验1设定相同的r、α、β、p0等参数，通过本文算法得到混叠矩阵的估计为：

由此计算出来的角度偏差如表3。

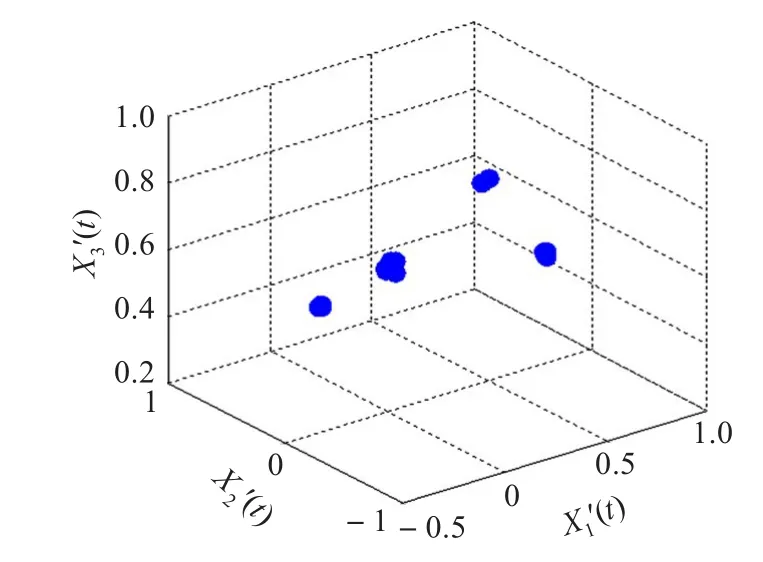
图6 混叠信号归一化到上半单位球

表3 原混叠矩阵与估计的混叠矩阵的角度偏差表

可以看出混叠矩阵各列向量之间的角度偏差均很小，混叠矩阵的估计精度较高。图7、8给出了源信号以及恢复的源信号，对比可以看出四路源信号得到精确分离，实际试听效果较好，有效实现了存在多路观测信号情况下的盲源分离。

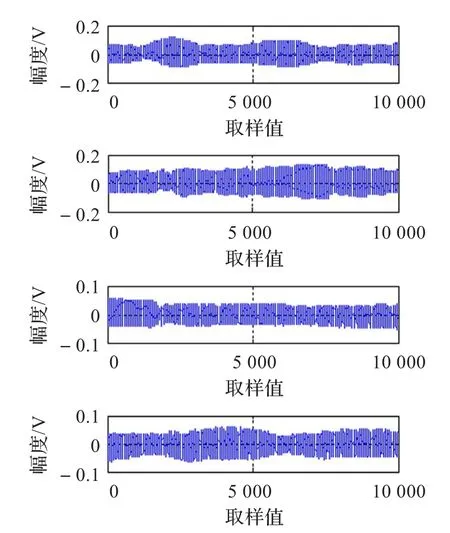
图7 四路源信号

图8 四路恢复信号

5 结论

本文提出了一种估计欠定盲源分离混叠矩阵的新方法，结合蚁群聚类算法，解决了源信号数目未知情况下的盲源分离问题，并且该方法适合于存在多个观测信号的情况。实验结果表明了本文方法的可行性与有效性。

[1]Cardoso J F.Blind signal separation：statistical principles[J]. Proc of IEEE：Special Issue on Blind Identification and Estimation，1998，90（10）：2009-2026.

[2]赵敏，谢胜利，肖明.欠定和非完全稀疏的盲源恢复[J].华南理工大学学报，2010，38（6）：19-23.

[3]Theis F J，Jung A，Puntonet C G，et al.Linear geometric ICA：fundamentals and algorithms[J].Neural Computation，2003，15：419-439.

[4]Bofill P，Zibulevsky M.Underdetermined blind source separation using sparse representations[J].Signal Process，2001，81（11）：2353-2362.

[5]Li Y，Andrzej C，Amari S.Analysis of sparse representation and blind source separation[J].Neural Computation，2004，16（6）：1193-1234.

[6]Sun T Y，Lan L E，Liu C C，et al.Mixing matrix identification for underdetermined blind signal separation：using hough transformandfuzzyk-meansclustering[C]//Proceedingsof IEEE International Conf on Systems，Man and Cybernetics，2009：1621-1626.

[7]Tan Beihai，Yang Zuyuan，Zhang Yuanjian.An underdetermined blind separation algorithm based on fuzzy clustering[C]//Proceedings of the 3rd International Conference on Innovative Computing Information and Control，Dalian，Liaoning，China，2008：404-408.

[8]王咏平，高俊.未知数量稀疏源的盲分离方法[J].华中科技大学学报，2007，35（12）：46-49.

[9]Dorigo M，Blum C.Ant colony optimization theory：a survey[J]. Theoretical Computer Science，2005，344：243-278.

[10]Colomi A，Dorigo M，Maniezzo V.Distributed optimization by ant colonies[C]//Proceedings of European Conference on Artificial Life.Paris，France：Elsevier，1991：134-142.

[11]Han Yanfang，Shi Pengfei.An improved ant colony algorithm for fuzzy clustering in image segmentation[J].Neurocomputing，2007，70：665-671.

[12]Marco D，Gianni D C，Luca M G.Ant algorithms for discrete optimization[J].Artificial Life，1999，5（2）：137-172.

[13]He Zhaoshui，Xie Shengli，Fu Yuli.Sparse representation and blind source separation of ill-posed mixtures[J].Science in China：Series F Information Sciences，2006，49（5）：639-652.

[14]谭北海，谢胜利.基于源信号数目估计的欠定盲分离[J].电子与信息学报，2008，30（4）：863-867.

WANG Fang,HE Xuansen

College of Information Science and Engineering,Hunan University,Changsha 410082,China

Taking advantage of the straight line clustering of the sparse source signals in underdetermined blind separation,a method of the mixing matrix estimation is proposed.The aliasing signals are standardized and the aliasing signals are formed spherical cluster,so the linear cluster is turned into density cluster.And then the clustering center is searched and obtained by using the ant clustering algorithm.The aliasing matrix and the source signals are accurately evaluated.The proposed algorithm can separate the source signals in which the number is unknown and it is also effective to separate three or more observed signals. The simulation results of speech signals show that this method can precisely separate and restore the original signals.

underdetermined blind separation;ant colony clustering;aliasing matrix

利用欠定盲源分离情况下稀疏源信号具有直线聚类的特点，提出了一种估计混叠矩阵的新方法。通过对混叠信号进行标准化处理，使混叠信号形成球形簇，将线性聚类转变成致密聚类；利用蚁群聚类算法对其进行搜索得到聚类中心，从而获得对混叠矩阵的精确估计。该方法能实现源信号数目未知情况下的欠定盲源分离，且能推广到三路或更多路观测信号的情况。对语音信号的仿真结果证明，该方法能精确地分离和恢复原始信号。

欠定盲分离；蚁群聚类；混叠矩阵

A

TN911.7

10.3778/j.issn.1002-8331.1110-0350

WANG Fang,HE Xuansen.Underdetermined blind separation based on ant colony clustering.Computer Engineering and Applications,2013,49（13）：211-215.

王放（1985—），男，硕士研究生，研究领域为盲源分离，随机信号处理；何选森（1958—），男，副教授，研究领域为随机信号处理，盲源分离，信息安全技术。E-mail：wangfang4227@163.com

2011-10-18

2012-01-02

1002-8331（2013）13-0211-05

CNKI出版日期：2012-03-21http://www.cnki.net/kcms/detail/11.2127.TP.20120321.1734.013.html

◎工程与应用◎