Haar小波滤波器序列只有两个非零项的论证

罗瑞评，张洪顺，陈勇，袁誉红

重庆通信学院 电磁频谱管理教研室，重庆 400035

Haar小波滤波器序列只有两个非零项的论证

罗瑞评，张洪顺，陈勇，袁誉红

重庆通信学院 电磁频谱管理教研室，重庆 400035

1 引言

小波是继傅里叶分析之后时频分析技术的一个重大突破，近几十年来，小波迅速发展并已成为图像处理和语音分析等众多领域的一种强有力的时频分析工具。目前，Haar小波是唯一严格反对称的实紧支撑正交小波基[1-2]，因其易于理解，计算速率快，具有较好的时（空）分辨率等优异特性，特别是在人脸识别、特征匹配搜索等领域应用更为广泛[3-4]。现有的小波构造均是在较特殊的情况下进行的，从而得到的小波仅是满足要求的小波族中的一部分[5]。然而，没有文献阐述小波函数和尺度函数（即尺度函数与低、高通滤波序列）之间是否具有相互唯一确定性。本文以多分辨分析为基础，在时域对Haar尺度函数与Haar小波低、高通滤波序列之间的相互唯一确定性进行了论证，得到了Haar滤波器序列只能含有两项非零系数。

2 多分辨分析（Multi-Resolution Analysis）

多分辨分析是由Mallat提出的对能量有限信号空间进行逼近的一般理论，其基本思想是在能量有限信号空间L2(R)的某个子空间中建立基底，然后通过伸缩和平移变换，把子空间的基底扩充到L2(R)中，以达到对信号的无限逼近。

由多分辨分析的定义可知，多分辨分析{ Vj}j∈Z是L2(R)的一个闭子空间列，且满足下面四个条件[5-6]。

（1）一致单调性：

（2）渐进完全性：

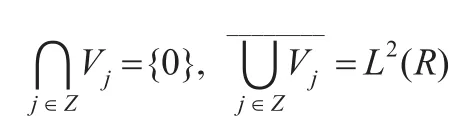
（3）伸缩规则性：

（4）正交基存在性：存在ϕ(t)∈V0，使得

是V0的标准正交基。其中ϕ(t)称为尺度函数（scaling function），Vj称为逼近空间。

3 小波函数的构造

在实际的信号处理中，信号f(t)一般会含有噪声，且一般噪声的频率比有用信号的频率高。将信号f(t)看做属于某个空间Vj+1，并对其进行正交分解，把f(t)中属于Vj+1但不属于Vj的部分（高频部分）去掉，达到对f(t)去噪的目的，这就产生了小波的概念[7-8]。

由多分辨分析的定义不难得出：

（1）{ϕj，k(t)}k∈Z是Vj的标准正交基；

（2）{ϕj，k(t)}k∈Z，j∈Z不是L2(R)的标准正交基，也不是L2(R)的框架，这簇向量对低频成分进行了无穷次度量，造成大量的冗余[9-10]。

为消除冗余，把嵌套空间Vj+1进行正交分解，即

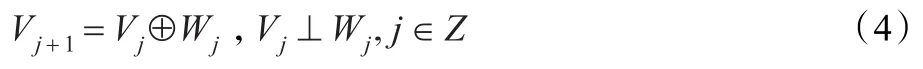
对Vj+1的这种分解有以下优点：

（2）Wj⊥Wk，j，k∈Z，j≠k；

（3）f(t)∈Wj⇔ f(2t)∈Wj+1， j∈Z，即由W0的标准正交基可求得Wj的标准正交基。

从而，只要寻找到ψ(t)满足：

（1）‖ψ(t)‖=1；

是W0的标准正交基；

则完成了小波函数的构造。

由式（1）～（4），可得：

式（7）和式（8）合称为双尺度方程，这是正交小波构造的核心[11]。在对数字信号的滤波中，关注的就是这两个双尺度方程的系数序列，即分别为低、高通滤波器的系数序列，hk称为低通滤波器系数，gk称为高通滤波器系数。

4 Haar小波只能含有两项高通滤波系数的证明

Haar尺度函数（Haar scaling function）ϕ(t)为：

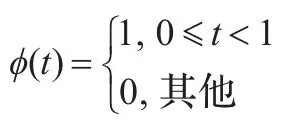
在绝大多数研究中均提出Haar小波函数ψ(t)为式（9）时，满足正交的要求，但没有论证在如前所述的Haar尺度函数下，只有这种小波函数才满足正交要求。

对比式（8）、（9），可以看出，Haar高通滤波器系数gk只有两项非零数值，也就是k只取了0、1。以下将在时域证明Haar多分辨分析中的Haar小波函数，只能有两项高通滤波器系数gk。

（1）嵌套空间的正交分解性[12]对Haar小波滤波系数的要求

由式（6）可得：

（2）Haar小波在同一尺度内的正交性对滤波系数的要求

由式（5）可知，对∀k，n∈z有：

满足式（10）和式（11）的要求，所以Haar小波的高通滤波器系数gk能取2个非零值。

即，当n=kl-k1时：

式（12）与式（11）的同一尺度内的正交性要求相矛盾，因此Haar小波的高通滤波器系数gk不能有l(l≥2，l∈Z)对偶奇相邻的非零值。

综上，Haar小波中只能含有两项非零值的高通滤波器系数。

5 结束语

本文中证明了Haar小波滤波器系数序列只能含有两个非零项，即Haar尺度函数与Haar小波函数之间相互唯一确定，进一步补充完善了Haar小波理论。本文的证明使得在小波应用中不用再关注Haar小波高通滤波器系数的个数问题，而把研究的重点放在Haar小波的具体变换应用中。

[1]陈勇，袁晓，罗丽芬，等.能量有限实序列对称性度量[J].四川大学学报：工程科学版，2008，40（3）：161-168.

[2]张池军，彭安金，王厚军，等.一类易于VLSI实现的对称双正交小波设计方法研究[J].电子与信息学报，2010，32（4）：973-974.

[3]Dogaru T，Carin L.Application of Haar-wavelet based multiresolution time-domain schemes to electromagnetic scattering problems[J].IEEE Trans on Antennas Propagate，2002，50（6）：774-784.

[4]范小春，邱政权.基于Haar小波的分级说话人辨识[J].计算机工程与应用，2010，46（11）：122-124.

[5]Chui C K.An introduction to wavelets[M].New York：Academic Press，1992.

[6]Mallat S.A wavelet tour of signal processing[M].2nd ed.Beijing：China Machine Press，2003.

[7]李波，朱庆生.正交小波基的构造及算法设计[J].重庆大学学报：自然科学版，1998，21（1）：113-115.

[8]Daubechies I.Ten lectures on wavelets[M].Philadelphia：SIAM，1992．

[9]王小春，宋瑞霞.一类正交函数系的离散表示及快速变换[J].计算机工程与应用，2008，44（8）：40-42.

[10]郎方年，袁晓，周激流，等.小波变换系数冗余性分析[J].自动化学报，2006，32（4）：568-573.

[11]刘明才.小波分析及其应用[M].北京：清华大学出版社，2005.

[12]朱铁稳，陈少强，李琦，等.一种完全重构双正交小波基的构造方法[J].电子与信息学报，2005，27（6）：900-903.

LUO Ruiping,ZHANG Hongshun,CHEN Yong,YUAN Yuhong

Radio Spectrum Management Staffroom,Chongqing Communication Institute,Chongqing 400035,China

Haar wavelet is widely used in such areas as image processing because of its short filter coefficients,which is one of Daubechies wavelets and is also the simplest compactly orthogonal wavelet.It is known that the existing orthogonal wavelets are constructed under certain conditions according to the theories of Daubechies wavelets construction；therefore,the uniqueness of Haar wavelet filter coefficients has been queried.There is only two nonzero values of Haar wavelet filter coefficients is proved by multi-resolution analysis theory in time domain,which is beneficial for theory consummation and application research of Wavelets.

Haar wavelet;filter coefficient;nonzero coefficient;uniqueness

Haar小波是最简单的紧支集正交小波（Daubechies小波），其滤波器序列较短，在图像处理等诸多领域都有广泛的应用。由Daubechies小波的构造理论可知，现有的正交小波是在比较特殊的前提下得到的，则Haar小波的滤波器系数序列的唯一确定性受到质疑。以多分辨分析为基础，在时域对Haar小波滤波器系数序列的唯一性进行了论证，即证明了Haar小波滤波器序列只有两个非零项，这对促进小波的理论完善与应用研究具有十分重要的意义。

Haar小波；滤波器系数；非零项；唯一性

A

TN911.6

10.3778/j.issn.1002-8331.1111-0097

LUO Ruiping,ZHANG Hongshun,CHEN Yong,et al.Demonstration of only two nonzero coefficients of Haar wavelet filter.Computer Engineering and Applications,2013,49（13）：191-193.

国家自然科学基金（No.61002034）。

罗瑞评（1985—），女，硕士研究生，研究方向为信号处理，电磁频谱管理；张洪顺（1949—），男，教授，研究方向为图像处理，小波理论及应用，无线电管理；陈勇（1975—），男，讲师，研究方向为图像处理，小波理论及应用。E-mail：lrp_hh@163.com

2011-11-10

2012-01-05

1002-8331（2013）13-0191-03

CNKI出版日期：2012-04-25http://www.cnki.net/kcms/detail/11.2127.TP.20120425.1722.077.html