基于鱼群算法的独立成分分析算法研究

张玉洁，李志明，宋广宇，凌加浠

中国地质大学 数理学院，武汉 430074

基于鱼群算法的独立成分分析算法研究

张玉洁，李志明，宋广宇，凌加浠

中国地质大学 数理学院，武汉 430074

1 引言

人工鱼群算法[1]（AFSA）是由李晓磊等人基于动物行为具有盲目性、自治性、突现性、并行性和适应性等特点，提出的一种群体智能优化算法。主要利用了鱼的聚群、追尾、随机和觅食行为，从单条人工鱼的行为开始进行研究，通过鱼群中每个个体在搜索空间中寻找食物所处的地方后，共享搜索结果，从而群体在整个搜索域中判断全局最优的过程。该算法收敛速度较快，对初值的选择不敏感，简单易操作，且具有避免陷入局部极值的良好能力。

独立成分分析（ICA）是在源信号和传输通道先验知识甚少的情况下，根据源信号的统计独立性，仅由观测信号推断出各个独立的源信号及传输通道的过程。ICA是20世纪90年代后期发展起来的一种新的信号处理的方法，由Herault和Jutten开创[2]。目前对ICA问题的研究已经涉及到信号处理、神经网络、人工智能、医学分析、图像处理等领域[3]。

ICA从提出到现在仅有二十几年的时间，却得到非常快的发展，各种算法纷纷涌现。ICA的算法基本形式可归结如下：

ICA算法=目标函数+优化算法

也即，围绕源信号的先验知识（如统计独立性）提出各种判断准则，构造一个以W为自变量的目标函数J(W)，然后结合各种优化算法来寻找分离矩阵W。如极大似然方法[4]、非线性PCA方法[5]、Infomax方法[6]、FastICA方法[7-8]、自然梯度方法[9-11]等。

本文首次将AFSA这种优化算法应用于ICA，该方法以负熵极大化为优化目标，利用人工鱼群在整个分离矩阵空间中的聚群、追尾、觅食和随机移动等行为达到搜索最佳分离矩阵的目的。

2 线性ICA问题的描述

假设瞬时线性ICA模型[2]：

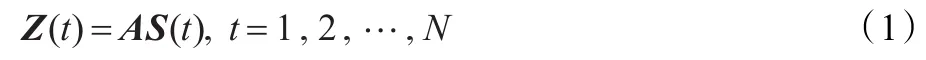
其中Z(t)=(z1(t)，z2(t)，…，zM(t))T是M维观测信号，S(t)= (s1(t)，s2(t)，…，sM(t))T是M维未知的、零均值的、相互独立的源信号，且si(t)，i=1，2，…，M中至多只有一个高斯信号。A∈RM×M是一个未知的列满秩的常数矩阵。

ICA的目的就是通过观测信号Z(t)寻找M×M分离矩阵W，再由分离矩阵和观测信号恢复出相互独立的源信号S(t)：

在不考虑排列顺序和幅度[2]前提下，Y(t)=(y1(t),y2(t),…,yN(t))T为S(t)的估计。

3 AFSA简介

人工鱼模型包括两个方面：变量和鱼群行为函数。在一个n维的空间中，有L条人工鱼组成一个群体，向量X=(x1，x2，…，xn)表示当前状态下的人工鱼，其中xi(i=1，2，…，n)为寻优参数；Φ=f(X)为人工鱼在位置X时对应的的食物浓度；Step表示移动步长；Visual为人工鱼的视野范围；表示第i和第j个人工鱼个体之间的距离；δ为拥挤因子；Trynumber表示人工鱼在每次迭代中的最大试探次数。

AFSA首先初始化一群人工鱼，通过不断的迭代，搜索最优解。在每次迭代过程中，人工鱼通过随机移动、觅食、聚群及追尾等行为来自我更新，具体过程如下所示。

（1）随机行为：鱼在其视野内随机地寻找食物。

（2）公告板：记录当次迭代中最优人工鱼所处位置Xbest及对应的食物浓度Φbest。每个人工鱼在移动的过程中，完成一次迭代后，就将自身所处地方的食物浓度与公告板中记录进行比较，如果优于公告板记录，则用自身所处位置及食物浓度更新公告板中的记录，否则，公告板不变。当整个算法的迭代结束后，最优值即是公告板上的结果。

（3）觅食行为[12]：随机移动的鱼主要向着食物多的方向移动。人工鱼当前位置Xi，在其视野范围内随机选择一个位置Xj：

其中i，j=1，2，…，n，rand为[0，1]之间的随机数。分别计算并比较Xi与Xj所对应的Φi与Φj，如果，Φj＞Φi，则Xi直接移动到Xj，反之，重新按式（3）随机选择Xj，判断是否满足前述的条件，反复尝试Trynumber次之后，如果仍不满足，则Xi按式（4）随机移动一步。

（4）聚群行为[1]：大量的鱼在游动过程中都会自然地聚集成群进行集体活动，同时避免过度拥挤。人工鱼当前位置为Xi，搜索目前邻域内dij＜Visable的伙伴数目nf，并计算中心位置-X，若-X所对应的函数值-Φ满足-Φ/nf＞δΦi且Φi＜-Φ，表示伙伴中心位置较优，食物浓度高，则Xi按式（5）移动一步，否则进行觅食。

（5）追尾行为[1]：当某条鱼发现食物时，附近的鱼会尾随而来，从而导致更远地方的鱼也跟过来。设人工鱼当前位置为Xi，搜索当前视野范围内对应函数值最优的伙伴Xb，如果最优值Φb满足Φb/nf＞δΦi且Φi＜Φb，则表明Xb的周围不太拥挤，Xi按（6）移动一步，否则进行觅食。

本文研究的是函数最大值的问题，先进行聚群、追尾等行为（也可先执行追尾行为，再执行聚群行为等），然后比较这些行为后每个个体所对应的函数值，选择函数值最大者对应的行为来执行。最终，大量人工鱼会聚集最优值的极值区域周围，从而达到搜索全局最值的目的。

4 基于AFSA的ICA算法

利用源信号之间的独立性，许多学者提出了不同的目标函数。本文采用负熵极大化作为评价准则[13]。

负熵的定义：

其中，pG(Y)与p(Y)表示具有相同均值和协方差矩阵的高斯密度函数。

目标函数为：

然而直接按式（7）估计负熵需要先估计概率密度函数，数值计算既繁琐又不稳健。文献[13]提出用Edgeworth展开逼近yi的概率密度函数，则目标函数化为：

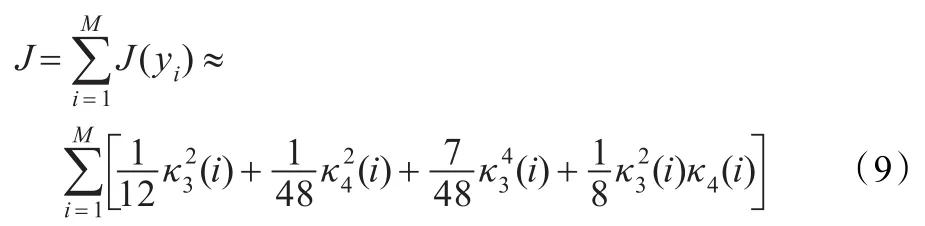
其中，κ3(i)=m3(i)，κ4(i)=m4(i)-3，mk(i)=E[(yi)k]。通过最大化式（9）得到分离矩阵W，进而得到源信号的估计。

为了简化计算，提高算法的精确度，一般在进行分离之前需要先对观测信号进行预处理。白化是一种常用的预处理方法[3]，即对混合信号Z做线性变换Ω(t)=VZ(t)，使得变换后的新信号Ω(t)的各个成分之间互不相关，具体作法为：对数据Z的协方差矩阵RZ=E{ZZT}进行特征值分解，U为以RZ的特征向量为列构成的矩阵，D是以RZ的特征值为对角元素的对角矩阵，则V=D-1/2UT。

由鱼群算法来确定分离矩阵W主要分为以下几步：

（1）白化观测信号Z得到Ω，使其满足E{ΩΩT}=I。

（2）初始化鱼群算法参数和人工鱼状态。

（3）按式（9）计算每条人工鱼所对应的负熵，并更新公告板。

（4）每条人工鱼按一定的条件执行觅食、聚群、追尾行为，并更新自己的状态。

（5）判断是否达到最大迭代次数，若达到最大迭代次数则执行步骤（6）；否则执行步骤（3）。

（6）选取全局最优位置构成分离矩阵W，Y=WZ则是源信号的估计。

5 模拟实验

为了验证算法的有效性，对以下信号进行计算机仿真实验。源信号为：

仿真实验中随机选取混合矩阵，样本点数N=5 000，人工鱼规模L=20，重复尝试次数Trynumber=10，Visual=0.25，Step=0.05，迭代次数为100，进行了50次Monte Carlo实验。图1给出了源信号与分离信号的波形图，其中横坐标表示样本点个数（选择前800个数据点），纵坐标是样本的幅度。从图中可以清楚看出除了在顺序和幅度上有一些差别外，分离后的信号在波形上与源信号保持了很好的一致性，混合信号得到了较好的分离。

图2给出了目标函数J全局平均最大值的进化曲线。从中可以看出随着人工鱼群的移动，目标函数不断优化，负熵在不断增加。在30次后就基本保持不变，迭代可以停止，此时函数值所对应的人工鱼所处位置即为分离矩阵的估计。

图2 函数J全局平均最大值的进化曲线

为了进一步描述算法的有效性，本文采用分离信号与源信号之间的信噪比作为性能指标[14]：

其中，yi是si对应的分离信号。50次Monte Carlo实验的平均信噪比结果为[33.767 5，31.425 2]。

最后将鱼群算法与自然梯度法进行盲源分离进行比较，其结果如表1。

表1 鱼群算法与自然梯度法进行盲源分离的比较

从表1中可以看出，鱼群算法用于盲源分离与自然梯度法相比较，其算法精度更高，且收敛速度更快。主要原因在于自然梯度法是一个局部最优算法，有可能取得局部极值，导致算法失败。并且当源信号幅度随时间快速变化时，会使自然梯度算法数值上不稳定。

6 结论

本文首次将鱼群算法引入到独立成分分析中，提出了一种基于人工鱼群优化的独立成分分析算法。用Edgeworth展开式得到基于负熵的目标函数，通过人工鱼寻优，得到全局最优解。计算机仿真实验验证了算法的有效性。人工鱼群算法目前还处于起步阶段，算法还不完善，在实验中发现视野与步长对算法的各种行为和收敛性能有较大影响，下一步将考虑自适应调整步长与视野的人工鱼群算法，并将其应用于ICA中，以期获得更为理想的效果。

[1]李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式：鱼群算法[J].系统工程理论与实践，2002，22（11）：32-38．

[2]Herault J，Jutten C.Blind separation of sources，Part I：an adaptive algorithm based on neuromimetic architecture[J].Signal Processing，1991，24（1）：1-10.

[3]Hyvarinen A，Oja E.Independent component analysis：algorithms and applications[J].Neural Networks，2000，13（4/5）：411-430.

[4]Pearlmutter B，Parra L.A context-sensitive generalization of ICA[C]//ProceedingsoftheInternationalConferenceon Neural Information Processing，1996：151-157.

[5]Oja E.The nonlinear PCA learning rule in independent component analysis[J].Neural Computing，1997，17（1）：25-45.

[6]Park H，Oh S，Lee S.A modified infomax algorithm for blind signal separation[J].Neurocomputing，2006，70（1/3）：229-240.

[7]Zhu X，Ye J，Zhang X.A fixed-point nonlinear PCA algorithm for blind source separation[J].Neurocomputing，2005，69（1/3）：264-272.

[8]Hyvarinen A，Oja E.Simple neuron models for independent component analysis[J].Neural Computation，2000，7（6）：671-687.

[9]Amari S.Natural gradient works efficiently in learning[J].Neural Computation，1998，10（2）：251-276.

[10]Amari S，Chen T，Cichocki A.Stability analysis of adaptive blind source separation[J].Neural Networks，1997，10（8）：1345-1351.

[11]Amari S，Cardoso J F.Blind source separation—Semiparametric statistical approach[J].IEEE Trans on Signal Processing，1997，45（11）：2692-2700.

[12]王联国，洪毅，施秋红.全局版人工鱼群算法[J].系统仿真学报，2009，21（23）：7483-7502.

[13]Girolami M.An alternative perspective on adaptive independent component analysis algorithm[J].Neural Computation，1998，10（8）：2103-2114.

[14]Lee T W，Girolami M，Bell A J，et al.A unifying information theoretical framework for independent component analysis[J]. Computers and Mathematics with Application，2000，31（11）：1-21.

ZHANG Yujie,LI Zhiming,SONG Guangyu,LING Jiaxi

School of Mathematics and Physics,China University of Geosciences,Wuhan 430074,China

Independent Component Analysis（ICA）which requires a little prior knowledge（such as independent）of signals is widely applied.The goal of ICA is to find a separation matrix so that each component of the output signal by transforming is independent.The key of ICA is to construct a target function,and then obtain the separation matrix by maximize（or minimize）the target function.This paper proposes an ICA algorithm based on Artificial Fish Swarm Algorithm（AFSA）.With the target function of maximum negentropy,it can obtain the separation matrix through foraging,cluster and tracing behavior of artificial fishes and updating artificial fish position.Compare with natural gradient,AFSA has the high accuracy and fast convergence rate.Experimental results are provided to evaluate the performance of the proposed algorithm.

Artificial Fish Swarm Algorithm（AFSA）;Independent Component Analysis（ICA）;negentropy

独立成分分析（ICA）只需要知道源信号较少的先验知识（如统计独立性等），仅由观测信号便能恢复出源信号的特性，因而得到了广泛应用。ICA的目的是寻找变换矩阵，使输出信号经变换后各成分之间尽可能的统计独立，其关键是建立一个目标函数，使得最大化（或最小化）目标函数的解便是所要找的变换矩阵。首次将人工鱼群算法（AFSA）与ICA相结合，提出了基于AFSA的独立成分分析算法。以负熵极大化作为目标函数，通过人工鱼的觅食，聚群和追尾行为，更新人工鱼的位置，得到全局最优解，从而得到分离矩阵。与自然梯度法相比，鱼群算法精度更高，收敛速度更快，仿真实验表明了将鱼群算法应用于独立成分分析的可行性和有效性。

人工鱼群算法；独立成分分析；负熵

A

TN911.72

10.3778/j.issn.1002-8331.1110-0594

ZHANG Yujie,LI Zhiming,SONG Guangyu,et al.New independent component analysis method based on fish swarm algorithm.Computer Engineering and Applications,2013,49（13）：187-190.

国家自然科学基金（No.11026145，No.61102103，No.61071188）；湖北省自然科学基金（No.2010CDB04205，No.2009CDB077）；中央高校基本科研业务费专项资金（No.CUGL090252，No.CUG090112，No.CCNU10A01013）。

张玉洁（1981—），女，博士，讲师，主要研究方向为时频分析和信号处理；李志明，男，博士，讲师；宋广宇，男，硕士研究生；凌加浠，男，硕士研究生。E-mail：zhangyujie@cug.edu.cn

2011-11-03

2012-01-18

1002-8331（2013）13-0187-04

CNKI出版日期：2012-03-21http://www.cnki.net/kcms/detail/11.2127.TP.20120321.1735.049.html