一种抑制SAR图像相干斑的空域滤波算法

朱磊，霍小波，吴江勇

1.西安工程大学 电子信息学院，西安 710048

2.西安电子科技大学 雷达信号处理国家重点实验室，西安 710071

一种抑制SAR图像相干斑的空域滤波算法

朱磊1，2，霍小波1，吴江勇1

1.西安工程大学 电子信息学院，西安 710048

2.西安电子科技大学 雷达信号处理国家重点实验室，西安 710071

1 引言

合成孔径雷达（SAR）由于其相干叠加的成像机制，导致在SAR图像中产生了一种称为相干斑（speckle）的随机乘性噪声[1]，而相干斑的存在严重扰乱了SAR图像的视觉质量，妨碍了特征提取、目标跟踪等后续解译处理技术的有效性。因此，抑制SAR图像中的相干斑，对于改善成像质量，提升后续解译技术的效果都具有十分重要的意义。

当前，SAR图像相干斑抑制方法已形成空域滤波、变换域滤波与偏微分扩散滤波三大类[2]。以经典的Lee滤波[3]、Frost滤波[4]及其改进算法[2，5]为代表的空域滤波，利用滑动窗口估计出的图像局部统计特性实施滤波，具有抑斑能力强，实时性好等优点，但相干斑抑制和边缘细节保护受窗尺度设置影响较大，容易出现部分区域的噪声抑制不充分现象。以小波[2，6]与Contourlet变换[7-8]等为代表的变换域滤波，根据变换域子带系数特征设计滤波策略，能有效抑制高频噪声，可较好地兼顾SAR图像同质区抑斑和边缘保护，但滤波前后须进行空域与变换域的分解与重构，复杂度高且计算量大，同时容易造成伪吉布斯现象。以各向异性扩散[9]及其改进算法[10-11]为代表的偏微分扩散滤波，借助图像局部结构特征来控制扩散的强度与方向，从而在抑斑与保护边缘上均取得了较好的效果，但容易造成图像动态范围减小以及扩散迭代次数设置不佳而产生的图像模糊或相干斑抑制不充分现象。

为兼顾SAR图像相干斑抑制与边缘保护，本文以负指数衰减型加权滤波模型为基础，提出了一种基于两次滤波策略的空域滤波新算法（SDF）。

图1 Lee滤波与Frost滤波在不同参数下的抑斑图像对比

2 经典的空域Lee滤波与Frost滤波

设在空域位置m=(x，y)处，SAR图像的观测模型可表示为：

其中，f为观测值，s为场景参数，n为乘性相干斑噪声。若设局域窗H的中心像素位置为m，其他像素相对位置为r，绝对位置为k=m+r，而、δf(m)与(m)分别表示m处像素观测值f在H窗内的局部均值、标准差与方差，加权滤波估计值为ˆ，则Lee滤波的加权滤波模型可表示为：

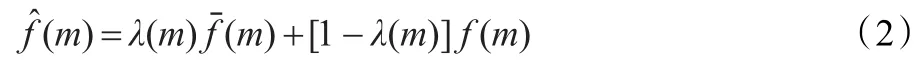
Frost滤波是一种MMSE准则下的负指数型加权滤波器，其模型可表示为：

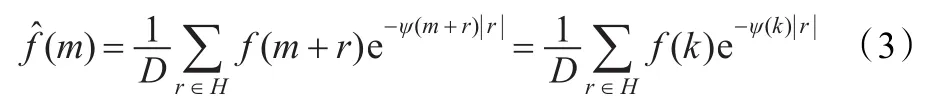
虽然同为空域滤波器，但两类滤波器却在抑斑效果上存在显著差异，图1显示了两类滤波的抑斑图像对比，从中可发现下列规律：（1）Frost滤波具有更强的噪声平滑能力，边缘区域噪声也能得到充分抑制，但容易造成边缘细节损失；（2）Lee滤波在同质区抑斑显著，而在边缘区域则又能有效阻止平滑，但边缘区域会由于噪声平滑不足而形成明显的边缘噪声带；（3）对于Frost滤波，当μ取较大值时，边缘保持性能较好而相干斑抑制性能较差，反之则相反；（4）对于Lee滤波，当窗尺度较小时，同质区相干斑抑制性能较差但边缘噪声带较窄，反之则相反。两类滤波在抑斑效果上的显著差异是由不同的滤波模型与加权系数估计方法共同决定的，Frost滤波采用负指数加权模型且衰减因子ψ(m)只受观测值f的变差系数控制，而Lee滤波则采用线性加权模型且权重系数λ(m)受观测值f与相干斑n的变差系数共同作用。可见，如果能将Frost滤波同Lee滤波按照某种合理的方案有机结合，则既可以利用Frost滤波较强的相干斑抑制能力有效抑制包括边缘区域在内的相干斑噪声，同时又能利用Lee滤波选择性的抑斑特点，有效防止边缘细节被过度平滑，最终实现带有边缘保护的相干斑抑制。而本文SDF算法，正是以Frost滤波提出的负指数型加权滤波模型为基础，用Lee滤波的加权系数λ(m)取代传统Frost滤波中的待定常数μ，并连同变差系数Cf及距离参数形成新的联合衰减因子ψ(m)，进而再由ψ(m)构成负指数型滤波加权系数e-ψ(m+r)|r|，实现可有效兼顾相干斑抑制与边缘保护的空域滤波。

3 基于两次滤波策略的空域滤波算法SDF

本文提出的SDF算法计算流程如图2所示。SDF算法先后经历了预滤波与精细滤波两次滤波处理，而两次滤波则具有完全相同的计算流程，主要区别为：加权滤波窗尺度不同，预滤波采用小尺度加权滤波窗H，而精细滤波采用较大加权滤波窗H；局部统计参量的估计对象不同，预滤波估计原始SAR图像f的局部统计参量，而精细滤波则对预处理SAR图像fˆ进行局部统计参量估计。

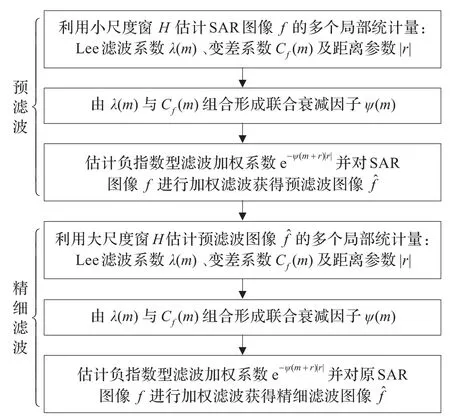
图2 SDF滤波算法的计算流程图

在对SAR图像进行精细滤波前，先进行预滤波处理。其目的是利用预滤波对SAR图像相干斑进行初步抑制，并为精细滤波提供能更精确反映SAR图像同质区与边缘区域分布特性的精细局域统计参量，从而使得精细滤波可以更为有效地抑制同质区相干斑，并防止边缘区域的细节被过度平滑。另外，预滤波采用小尺度窗是为在初步抑制SAR图像相干斑的同时，尽量防止边缘细节被平滑，而由于向精细滤波提供了更精细的局域统计参量，故可以利用大尺度窗来充分抑制同质区相干斑而不会过度平滑边缘。由于两次滤波具有相同的计算流程，因此下面给出一次滤波的详细计算过程。

3.1 估计多种局部统计参量

需要估计的局域统计参量包括：Lee滤波的加权系数λ(m)、变差系数Cf(m)及距离参数|r|。由于距离参数|r|计算比较简单，这里主要讨论λ(m)与Cf(m)，另外，考虑到Lee滤波加权系数可表示为：

因此，实质上需要估计的局部统计参量，只有SAR图像观测值f(m)的变差系数Cf(m)与相干斑n(m)的变差系数Cn(m)。为了便于和前面的加权滤波窗H区别，这里假设Cf(m)与Cn(m)由局域窗G估计（窗尺度为a×a，中心像素位置为m，其他像素的相对位置为r，绝对位置为k=m+r）。

f(m)在窗G下的变差系数Cf(m)可表示为：

由于SAR图像中具有相同统计分布的相干斑，因此，SAR图像各像素相干斑的变差系数Cn(m)也均用同一估计值表示。Cn(m)的常用估计方法是：在SAR图像中找出一块同质区，然后在选定区域按式（5）估计。但这种估计方法不仅需要人为参与选择估计区，而且一块同质区相干斑的Cn(m)变化很难代表整幅SAR图像相干斑Cn(m)的变化情况。为此，本文给出了一种简单有效的SAR图像相干斑Cn(m)估计方法。具体步骤是：先利用式（5）估计SAR图像各像素点的Cn(m)，然后利用直方图方法统计各像素点Cn(m)估计值最集中的数据值，而这个数据值就是最终的全局相干斑Cn(m)值。该估计方法的提出是基于一般SAR图像均满足其大部分区域均为同质区这一假设；另外，该方法简单易行，利用直方图统计方法巧妙地将图像边缘与复杂纹理区域中不准确的Cn(m)估计值剔除，能反映出抑斑SAR图像分布最集中的相干斑Cn(m)值。

3.2 估计负指数衰减型加权系数

本文SDF算法采用了与Frost滤波相同的负指数衰减型加权滤波模型。如式（3）所示，传统Frost滤波的加权系数仅由衰减因子ψ(k)与距离参数|r|决定，当局域窗H的尺度确定后，|r|的作用就完全固化，而Frost滤波加权系数的大小就由ψ(k)决定。由前面讨论可知，Frost滤波中ψ(k)=μCf(k)，当μ取较小值时，相干斑抑制性能较好而边缘保持性能较差，反之则相反，这说明传统Frost滤波中将μ设为常数不能兼顾相干斑抑制与边缘保护。如果能找到一种自适应变化的局部统计参量来代替常系数μ，且该参量能在SAR图像同质区取较小值，而在边缘区域取较大值，那么Frost滤波就可以有效兼顾相干斑抑制与边缘保护，而Lee滤波加权系数的倒数1 λ就满足上述要求。因此，本文提出的SDF算法将Lee滤波加权系数λ、变差系数Cf与距离参数|r|结合形成新的加权系数，具体计算方法是：

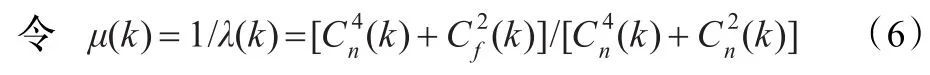
同时，设联合衰减因子为：

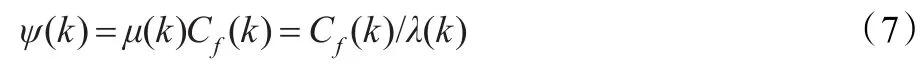
则新的负指数型加权系数可表示为：

下面，分析μ(k)的性能。其一，在SAR图像同质区，由于Cf(k)与Cn(k)接近，故μ(k)趋近于1，而在边缘区域一般Cn(k)较小而Cf(k)较大，故μ(k)明显大于1。因此，μ(k)能随图像区域自适应变化，在SAR图像同质区取值较小，而在边缘区域取值较大，从而兼顾相干斑抑制与边缘保护。其二，对原始SAR图像先进行预滤波处理以初步抑制相干斑，然后再估计SAR图像的局部统计参量，则Cn(k)会迅速减小，而Cf(k)在同质区也迅速减小，但在边缘区域变化却不显著，这样导致在同质区μ(k)为一有限值，而在边缘区域μ(k)则迅速趋近于无穷大。因此，μ(k)能借助预滤波的进行，在边缘区域控制加权系数e-ψ(k)|r|趋近于0，从而有效防止对边缘区域的过度平滑，同时，在同质区控制加权系数e-ψ(k)|r|趋近于1，从而在同质区加大对相干斑的抑制力度。

下面，结合图1（a）所示仿真SAR图像说明滤波参数对抑斑的影响。图3显示了三种空域滤波算法在参数图像与抑斑图像上的差异，容易发现：相对图3（a）与图3（b），图3（c）所示抑斑参数图像的边缘区域界定最完整最清晰，同质区斑状起伏也最小，而同质区与边缘区域的对比度也最大，这说明SDF算法能更好地兼顾边缘区域保护与同质区相干斑抑制；图3（d）～图3（f）所示的抑斑图像比也能验证这一点，显然，图3（f）边缘清晰完整，没有图3（d）的边缘模糊现象，也没有图3（e）的边缘噪声带，同时，图3（f）同质区也更平滑，没有图3（d）中明显的斑状起伏，也没有图3（e）中散布的点噪声。图4展示了SDF算法的预滤波与精细滤波在参数图像与抑斑图像上的差异。很明显，SDF精细滤波的ψ(k)图像与抑斑图像均要明显优于预滤波，这说明SDF算法采用两次滤波策略，确实可有效提高对SAR图像同质区相干斑的抑制与边缘区域细节的保护。

图3 三类空域滤波算法的参数图像与抑斑图像对比

图4 SDF预滤波与精细滤波的参数图像与抑斑图像对比

3.3 形成负指数衰减型加权滤波

利用式（6）～（8）估计获得的负指数加权系数，就可以形成负指数衰减型加权滤波：

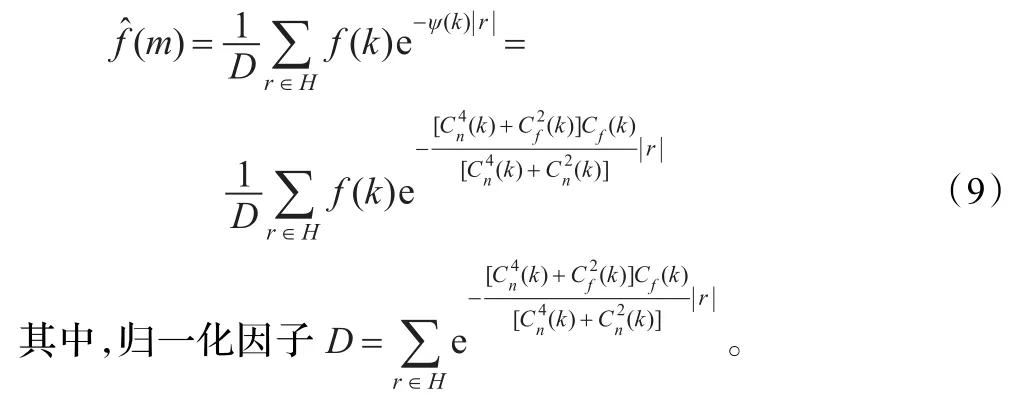
4 仿真实验

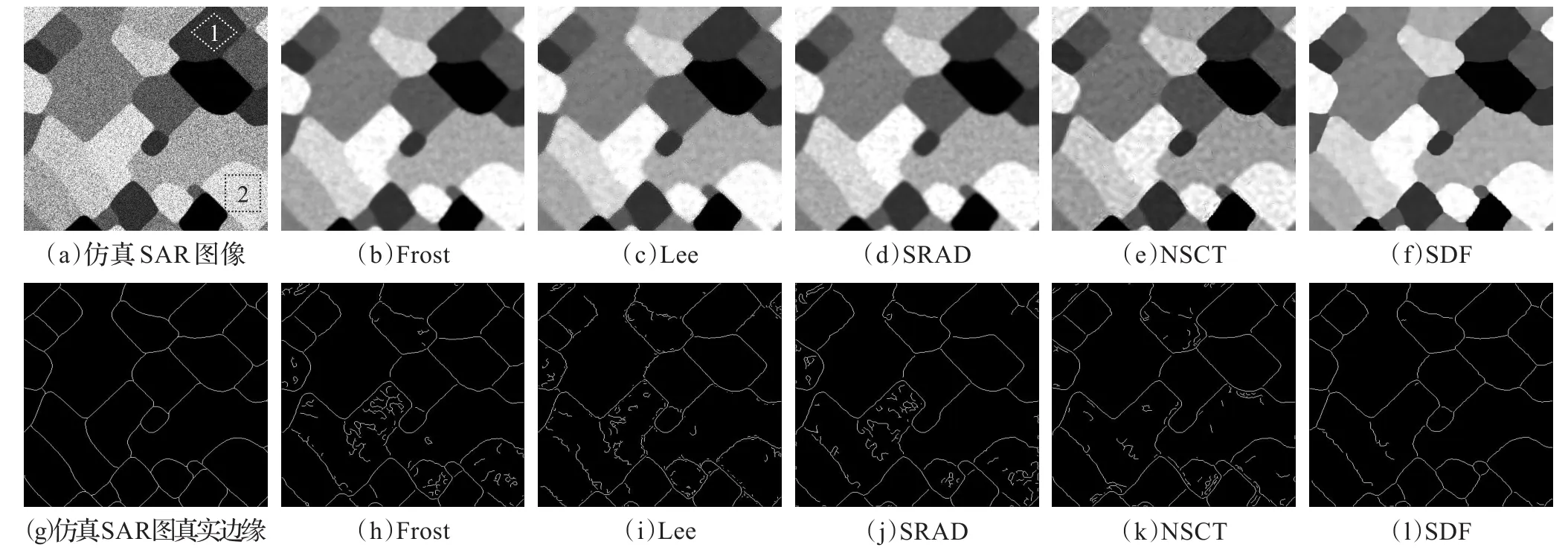
图5 各算法对仿真SAR图像的抑斑效果对比

图6 各算法对真实SAR图像的抑斑效果对比

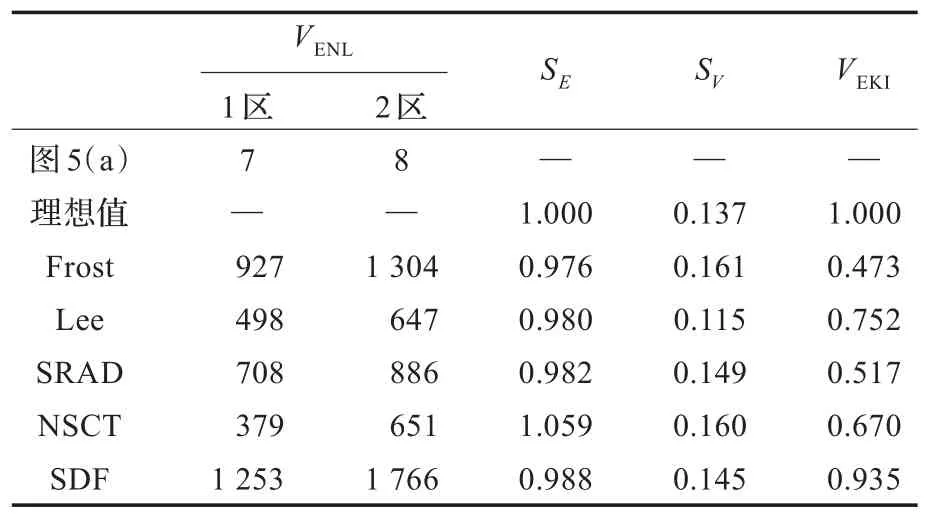
表1 各算法对仿真SAR图像的抑斑参数对比

实验中各算法主要参数设置如下：

（1）Frost滤波与Lee滤波均采用尺度为11×11的矩形窗；

（2）SRAD滤波迭代运算150次，时间步长0.05；

（3）NSCT滤波采用3层分解，各层方向子带数为：8，8，16；

（4）SDF算法加权滤波窗H的尺度为11×11，局域量估计窗G的尺度为5×5；

（5）VENL采用图5（a）与图6（a）中虚线框选定的尺度为40×40的同质区作为计算区域，而SE与SV的计算区域则为整个图像。

一方面，从表1和表2所示的抑斑参数对比来看，SDF算法无论是在评价抑斑能力的VENL与SV两项指标上，还是评价图像边缘保护与辐射保持能力的VEKI与SE两项指标上，均优于其他算法。另一方面，从图5和图6所示的抑斑效果的直视比较可以发现：SDF算法获得的抑斑图像图5（f）与图6（g）均匀区域均比其他算法更平滑，没有图5（b）与图6（c）的边缘细节损失现象，没有图5（c）与图6（d）中明显的孤立点噪声与边缘噪声带散布，没有图5（d）与图6（e）的图像边缘模糊现象，也不存在图5（e）与图6（f）中的虚假条纹；从抑斑图像边缘保护方面来看，SDF算法获得的边缘检测结果图5（l）与图6（l）与其他算法边缘检测结果（图5（h）～图5（k）与图6（h）～图6（k））相比，虚假边缘最少，检测出的边缘最接近图像的真实边缘。综上，从目视效果与定量指标比较来看，SDF算法对仿真SAR图像与真实SAR图像在抑斑与边缘保护方面，均较其他算法理想。

5 结束语

为兼顾SAR图像的相干斑抑制与边缘保护，以负指数衰减型加权滤波模型为基础，提出了一种基于两次滤波策略的SDF滤波新算法。SDF算法利用多种局部统计参量形成联合衰减因子，而由联合衰减因子形成的负指数型加权系数不仅与SAR图像区域分布特性相适应，而且由于更多局域统计信息的融入，还为滤波中加强边缘保护提供了更有效的联合检测统计量。同时，采用两次滤波策略，先由预滤波初步削弱SAR图像相干斑噪声并估计获得更精准的局部统计参量，然后再借助精细局部统计参量对原SAR图像实施精细滤波，从而在抑制相干斑的同时，还能有效阻止边缘细节被过度平滑。

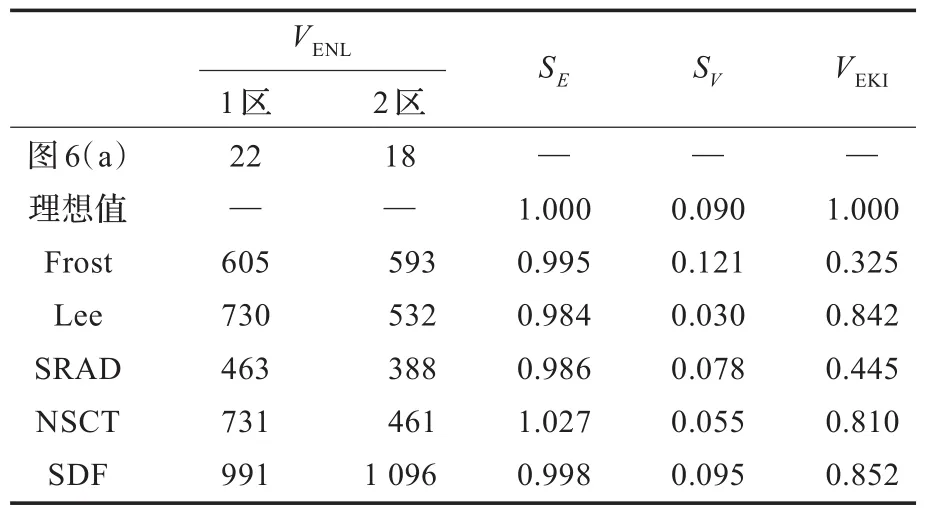
表2 各算法对真实SAR图像的抑斑参数对比

[1]Lee J S，Eric P.Polarimetric radar imaging：from basics to application[M].Boca Raton：CRC Press of Taylor&Francis Group，2009：101-175.

[2]朱磊，水鹏朗，武爱景.一种SAR图像相干斑噪声抑制新算法[J].西安电子科技大学学报，2012，39（2）：80-86.

[3]Lee J S.A simple speckle smoothing algorithm for synthetic aperture radar images[J].IEEE Trans on System，Man，and Cybernetics，1983，13（1）：85-89.

[4]Frost V S，Stiles J B，Shanmugan K S，et al.A model for radar images and its application to adaptive digital filtering of multiplicative noise[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1982，4（2）：157-166.

[5]朱磊，水鹏朗，章为川.利用区域划分的合成孔径雷达图像相干斑抑制算法[J].西安交通大学学报，2012，46（10）：83-89.

[6]Yu Y，Acton S.Speckle reducing anisotropic diffusion[J].IEEE Transactions on Image Processing，2002，11（11）：1260-1270.

[7]Liu Guojin，Zeng Xiaoping，Tian Fengchun，et al.Speckle reduction by adaptive window anisotropic diffusion[J].Signal Processing，2009，89（11）：2233-2243.

[8]Yu Jinhua，Wang Yuanyuan，Shen Yuzhong.Noise reduction and edge detection via kernel anisotropic diffusion[J].Pattern Recognition Letters，2008，29（10）：1496-1503.

[9]Bhuiyanr M I H，Ahmad M O，Swamy M N S.Spatially adaptive wavelet-based method using the Cauchy prior for denoising the SAR images[J].IEEE Transactions on Geoscience and Remote Sensing，2007，17（4）：500-507.

[10]贾建，陈莉.基于双变量模型和非下采样Contourlet变换的SAR图像相干斑抑制[J].电子与信息学报，2011，33（5）：1088-1094.

[11]常霞，焦李成，刘芳，等.基于斑点方差估计的非下采样Contourlet域SAR图像去噪[J].电子学报，2010，38（6）：1-6.

ZHU Lei1，2,HUO Xiaobo1,WU Jiangyong1

1.Electronics and Information College,Xi’an Polytechnic University,Xi’an 710048,China
2.National Key Lab of Radar Signal Processing,Xidian University,Xi’an 710071,China

In order to preserve edge characteristics and effectively reduce multiplicative speckle noise in SAR image,a new spatialdomain filtering algorithm is proposed.The new algorithm is based on the negative-exponential and weighted filtering model, and the weighting coefficients are produced by the decay factor obtained by combining several local statistics and are adaptive to the characteristics of regional distribution of SAR image.Meanwhile two-stage filtering strategy is used.The pre-filtering is executed for reducing speckle in SAR image and estimating fine local statistics,and the fine filtering for original SAR image is carried out based on the fine local statistics obtained by the pre-filtering.The experimental results show that compared with most existing despeckling algorithms,the proposed algorithm has better performance in the speckle suppression and edge preservation.

Synthetic Aperture Radar（SAR）image;speckle reduction;spatial-domain filtering;edge preservation

为在保护SAR图像边缘特征的同时有效抑制乘性相干斑噪声，提出了一种空域滤波新算法。该算法以负指数衰减型加权滤波模型为基础，通过将SAR图像多种局部统计参量巧妙结合作为联合衰减因子，形成与SAR图像区域分布特性相适应的负指数型加权系数；同时采取两次滤波策略，先由预滤波削弱SAR图像相干斑噪声并估计获得更精准的局部统计参量，然后借助精细局部统计参量再对原SAR图像实施精细滤波。实验结果表明，与多种抑斑算法相比，该算法在SAR图像抑斑与边缘保护方面均获得了更好的性能。

合成孔径雷达图像；相干斑抑制；空域滤波；边缘保护

A

TN911.73

10.3778/j.issn.1002-8331.1302-0072

ZHU Lei,HUO Xiaobo,WU Jiangyong.Spatial-domain filtering algorithm for speckle reduction of SAR images.Computer Engineering and Applications,2013,49（13）：165-169.

陕西省教育厅自然科学基金(No.11JK0983)。

朱磊（1979—），男，博士研究生，副教授，研究领域为信号与信息处理，嵌入式系统应用；霍小波（1985—），男，硕士研究生，研究领域为信号与信息处理；吴江勇（1987—），男，硕士研究生，研究领域为工业领域嵌入式系统应用。E-mail：zhulei791014@163.com

2013-02-11

2013-03-30

1002-8331（2013）13-0165-05

CNKI出版日期：2013-04-18http://www.cnki.net/kcms/detail/11.2127.TP.20130418.1614.010.html

◎信号处理◎