一种快速的广义噪声聚类算法

武斌，武小红，贾红雯

1.安徽农业大学 信息与计算机学院，合肥 230036

2.滁州职业技术学院 信息工程系，安徽 滁州 239000

3.江苏大学 电气信息工程学院，江苏 镇江 212013

4.江苏大学 食品与生物工程学院，江苏 镇江 212013

一种快速的广义噪声聚类算法

武斌1，2，武小红3，4，贾红雯2

1.安徽农业大学 信息与计算机学院，合肥 230036

2.滁州职业技术学院 信息工程系，安徽 滁州 239000

3.江苏大学 电气信息工程学院，江苏 镇江 212013

4.江苏大学 食品与生物工程学院，江苏 镇江 212013

1 引言

模糊聚类是模式识别领域中一个重要的分支，属于无监督的机器学习算法。其中最著名的模糊聚类算法是由Dunn提出[1]并由Bezdek加以扩展而形成的模糊C-均值聚类（FCM）。FCM算法及其派生算法在模式识别，图像处理和视频检索等领域取得很好的效果[2-4]。但是建立在可能性约束条件基础上的FCM对噪声非常敏感[5]，为了克服这个缺点，Krishnapuram和Keller放弃了FCM算法的可能性约束条件，提出了可能C-均值聚类（PCM）算法[5]。PCM算法能够聚类包含噪声的数据，它赋予噪声数据很小的隶属度值，因而噪声对聚类的影响可以忽略。但是PCM算法对初始聚类中心很敏感，常常会导致一致性聚类结果[6]。

Davé提出噪声聚类（NC）算法以处理噪声数据[7]。NC算法将噪声看做一个独立的类，定义噪声距离为常数δ。受PCM的启发，Davé认为噪声距离不是常数将提高算法的性能，因而定义噪声距离在不同的类中距离值不同，将噪声聚类算法扩展为广义噪声聚类（GNC）算法[8-9]。GNC算法实际上综合了FCM算法和PCM算法两者的优点，避免了FCM算法对噪声数据敏感和PCM算法易导致一致性聚类结果的缺点。但是，GNC算法在计算噪声距离时需要事先运行FCM算法以计算参数ηi，也就是说GNC算法非常依赖参数ηi。如果GNC算法算法不依赖参数ηi则不必事先运行FCM算法，这样必然节省了聚类时间。受可能聚类算法（PCA）[10]和可能性模糊C-均值聚类新算法[11]启发，本文提出一种快速的广义噪声聚类（FGNC）算法。FGNC算法不依赖参数ηi，比GNC聚类时间少，具有较高的聚类准确率。

2 噪声聚类和广义噪声聚类

噪声聚类（NC）算法定义噪声距离为常数δ。噪声被看做一个独立的类，对于某个数据点xj在噪声类中的隶属度定义为[7]：

式（1）中，c是聚类的类别数，uij是数据xj隶属于类i的隶属度值。NC采用的可能性约束条件如下：

约束条件（2）比FCM的可能性约束条件要宽松。

与FCM算法相比，NC算法的优点在于其鲁棒性和适合处理噪声数据。NC算法赋予噪声数据很小的隶属度值从而使噪声数据和真实数据区别开来。但是如何确定噪声距离常数δ是一个难点，通常要根据经验取值。

NC算法的噪声距离δ2和可能C-均值聚类（PCM）的参数ηi比较相似。PCM算法中实际上有c个噪声类而NC算法就一个噪声类，即NC算法是鲁棒的FCM算法，而PCM算法像c个NC算法的集合[8]。在分析NC算法和PCM算法基础上，Davé进一步将NC算法推广为广义噪声聚类（GNC），GNC最小化以下目标函数[8-9]：

式（3）中，Dik=‖xk-νi‖，表示数据点xk到类中心矢量νi的欧式距离。定义为：

式（4）中，参数ηi来自PCM的计算公式与FCM的隶属度计算公式相同，它们分别为[9]：

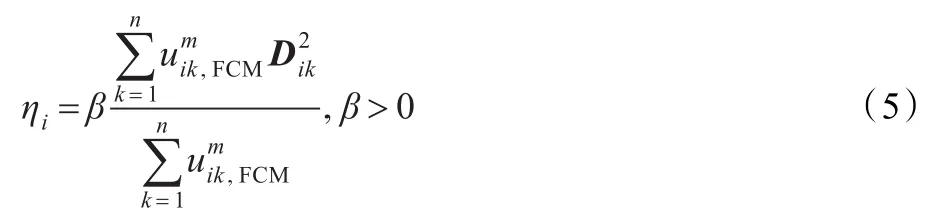
式（5）中，uik，FCM是运行FCM后得到的隶属度值，β通常取值为1。

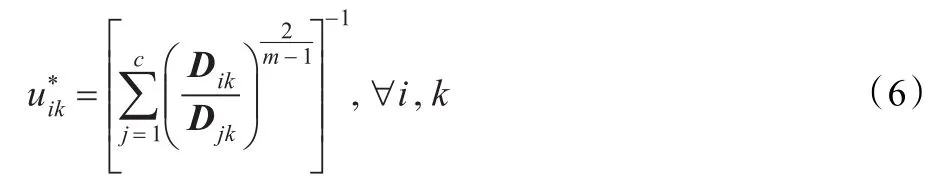
最小化式（3）得到GNC的隶属度：

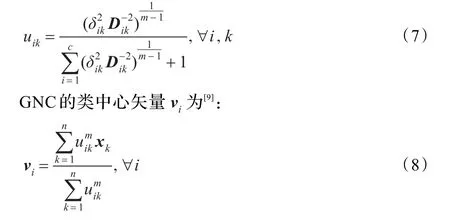
3 非参数化的广义噪声聚类

FGNC算法的类中心矢量νi和公式（8）一样。

理论分析：样本的协方差σ2衡量了数据的分离程度，联合式（10）和（11）可以将目标函数（3）变换为：

求解最小化式（13）得到的隶属度和式（12）相同式。式（13）的第1项为：

tr(SfW)衡量数据的类内紧凑程度，tr(ST)衡量数据的分离程度[10]。因而FGNC算法能同时重视数据的类内紧凑程度和分离程度，很好地解决了GNC依赖参数问题，同时具有良好的聚类效果。

FGNC算法可以表述如下。

初始化部分：

步骤1固定c和m的值，1＜c＜n，1＜m；设置终止值ε；

步骤2设置初始循环数r=1和最大循环数为rmax；

步骤3选定初始类中心V(0)；

步骤4根据公式（11）计算σ2的值。

循环计算部分：

步骤1根据公式（6）和（10）计算；

步骤2用公式（12）计算隶属度U(r)；

步骤3用公式（8）计算类中心矩阵V(r)；

步骤4循环数r加1，直到满足条件‖V(r)-V(r-1)‖＜ε或(r＞rmax)。

4 实验

为了测试FGNC算法的有效性、聚类准确性和聚类时间，分别用FCM、GNC和FGNC算法对一些数据集进行测试。实验条件：ε=0.000 01，最大循环数为rmax=100，m=2.0。计算机配置：奔腾1.7 GHz，内存256 MB，利用Matlab 7.0进行仿真计算。对三种算法的实验结果进行比较，说明了FGNC算法的优越性能。

4.1 对噪声数据的处理能力

[12]进行实验。X12是有12个数据点的二维数据集，它的坐标的分布图见文献[12]。X12中的10个数据点（除了点x6和x12）组成两个菱形分布在y轴两边，x6和x12到两类中心距离相等是噪声点。初始化类中心[12]：

分别对X12运行FCM、GNC和FGNC算法后，得到的隶属度值如表1所示。数据点x6和x12在运行FCM算法后每个类的隶属度均为0.50，因此FCM无法将噪声和其余的10个数据点区别开来，也就是说FCM算法对噪声敏感[12]。因为x12比x6远离类中心点，所以原则上要求x12的隶属度要比x6的隶属度小，而运行GNC算法后数据点x6和x12在每个类的隶属度分别为0.21和0.03，因此GNC算法能很好地把噪声数据从其他数据中区别开来。运行FGNC算法后，数据点x6和x12在每个类的隶属度分别为0.09和0.01，因此FGNC算法也能很好地处理噪声数据。实验表明GNC和FGNC算法均能有效地处理含噪声的数据，不同之处在于GNC需要运行FCM后来计算参数ηi，而FGNC则不需要。

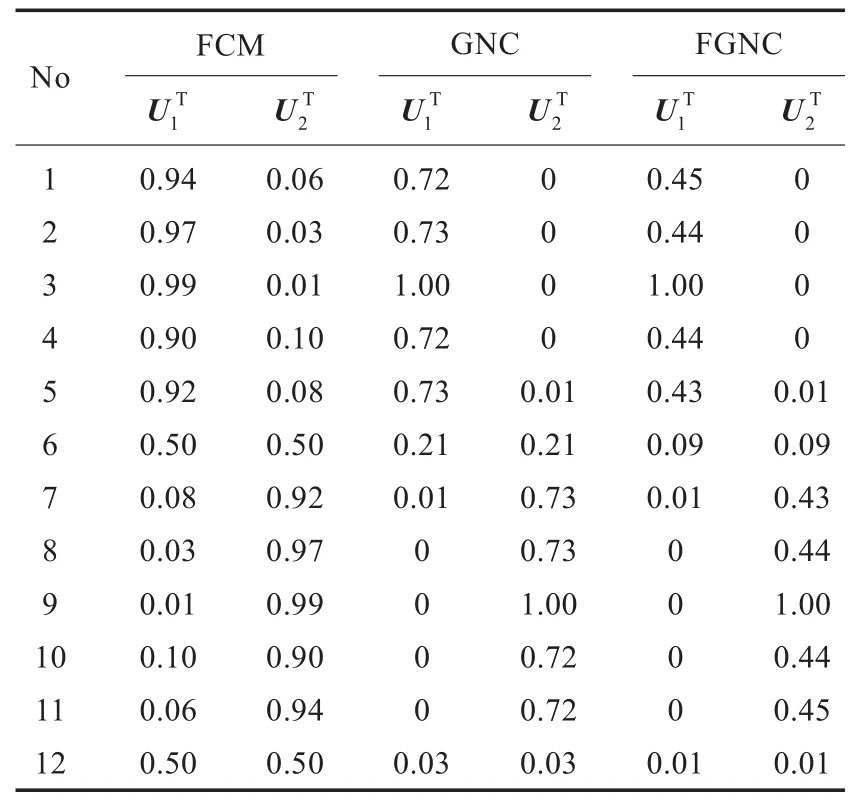
表1 FCM、GNC和FGNC算法对数据集X12进行实验所得到的隶属度

4.2 聚类中心分析

聚类算法除了产生隶属度外还会得到聚类的类中心，如果所得到的聚类中心距离真实聚类中心最近，则表示该算法得到的聚类中心最好。X12的真实聚类中心[12]：

表2是FCM、GNC和FGNC三种算法对噪声数据集X12进行实验所得的聚类中心。

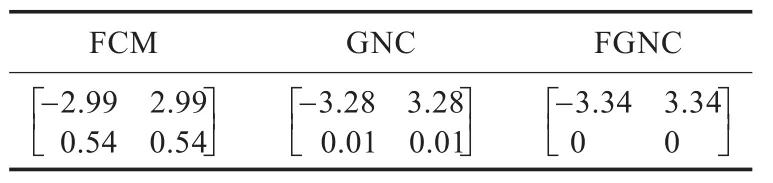
表2 FCM、GNC和FGNC算法对噪声数据集X12进行实验所得的聚类中心

用VFCM、VGNC和VFGNC分别表示表2中的类中心，利用下式计算类中心[12]：

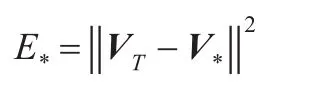
式中*表示FCM/GNC/FGNC算法。计算结果为：EFCM= 0.587 2，EGNC=0.007 2，EFGNC=0，则EFCM＞EGNC＞EFGNC。很明显E*越小表示该聚类中心越接近真实聚类中心，所以FGNC算法得到的类中心最好，GNC算法次之，FCM算法最差。

4.3 聚类准确性和聚类时间

对IRIS[13-14]数据集运行FCM、GNC和FGNC算法。初始化类中心[12]：

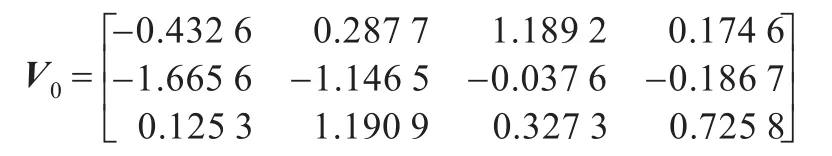
FCM、GNC和FGNC算法对IRIS数据集聚类的结果如表3所示，可见，FCM算法聚类准确率最差，聚类花费时间最少；GNC算法和FGNC算法聚类准确率相同，但FGNC花费时间比GNC要少，循环次数也比GNC少。

表3 FCM、GNC和FGNC算法对IRIS数据集聚类结果

接着对Wine数据集[15]做实验，Wine数据集有三类数据，三类数据点数分别是59、71和48，取属性7和10作为聚类实验用数据集。初始化类中心：

实验结果如表4所示，可见，FGNC算法聚类准确率最好，同时FGNC算法聚类花费的时间也比GNC算法少。

表4 FCM、GNC和FGNC算法对Wine数据集聚类结果

最后，对数据集X500进行聚类，X500含有两个类别的正态分布N(u，Σ)，分别为：

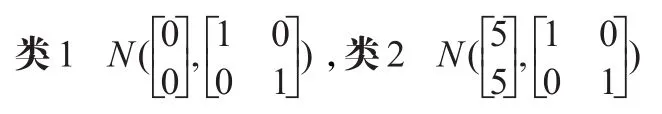
类1和类2分别含有200个数据点。另外，由100个非正态分布在[1，8]×[-4，4]上的噪声数据点构成X500的一个噪声类别。从表5可看出，FGNC算法聚类的循环次数和聚类时间均比GNC算法少。

表5 GNC和FGNC算法对X500数据集聚类结果

5 结论

本文在分析GNC算法的基础上，针对GNC算法需要事先运行FCM算法以计算其参数这个缺点，提出FGNC算法。通过对噪声数据的处理，以及对聚类中心分析，聚类准确率和聚类时间的实验分析，结果表明FGNC算法在保持GNC算法处理噪声数据能力的同时，具有最优的聚类中心，其聚类速度更快，聚类准确率更高。

[1]Dunn J C.A fuzzy relative of the ISODATA process and its useindetectingcompact well-separatedclusters[J].Journal of Cybern，1974，3（3）：32-57.

[2]Tjhi W C，Chen L H.A heuristic-based fuzzy co-clustering algorithmforcategorizationofhigh-dimensionaldata[J]. Fuzzy Sets and Systems，2008，159（4）：371-389.

[3]Lin D T，Liao G J.Swarm intelligence based fuzzy c-means clustering for motion vector selection in video watermarking[J]. International Journal of Fuzzy Systems，2008，10（3）：185-194.

[4]Ghosh A，Mishra N S，Ghosh S.Fuzzy clustering algorithms for unsupervised change detection in remote sensing images[J]. Information Sciences，2011，181（4）：699-715.

[5]Krishnapuram R，Keller J.A possibilistic approach to clustering[J]. IEEE Trans on Fuzzy Systems，1993（2）：98-110.

[6]Barni M，Cappellini V，Mecocci A.Comments on“a possibilistic approach to clustering”[J].IEEE Trans on Fuzzy Systems，1996，4（3）：393-396.

[7]Davé R N.Characterization and detection of noise in clustering[J]. Pattern Recognition Letters，1991，12（11）：657-664.

[8]He Guangpu，Li Min，Wu Bin，et al.Generalized noise clustering based on non-Euclidean distance[J].Journal of Beijing Jiaotong University，2008，32（6）：98-101.

[9]Davé R N，Sen Sumit.Generalized noise clustering as a robust fuzzy C-mestimators model[C]//Proceedings of Conference of the North American Fuzzy Information Processing Society，1998：256-260.

[10]Yang M S，Wu K L.Unsupervised possibilistic clustering[J]. Pattern Recognition，2006，39（1）：5-21.

[11]武小红，周建江.可能性模糊C-均值聚类新算法[J].电子学报，2008，36（10）：1996-2000.

[12]Pal N R，Pal K，Bezdek J C.A possibilistic fuzzy c-means clusteringalgorithm[J].IEEETransonFuzzySystems，2005，13（4）：517-530.

[13]Lee S W，Kim Y S，Park K H，et al.Iterative Bayesian fuzzy clustering toward flexible icon-based assistive software for the disabled[J].Information Sciences，2010，180（3）：325-340.

[14]Carl G L.Fuzzy connectivity clustering with radial basis kernel functions[J].Fuzzy Sets and Systems，2009，160（13）：1868-1885.

[15]Wang C H.Apply robust segmentation to the service industry using kernel induced fuzzy clustering techniques[J].Expert Systems with Applications，2010，37（12）：8395-8400.

WU Bin1，2,WU Xiaohong3，4,JIA Hongwen2

1.School of Information and Computer Science,Anhui Agricultural University,Hefei 230036,China
2.Department of Information Engineering,Chuzhou Vocational Technology College,Chuzhou,Anhui 239000,China
3.School of Electrical and Information Engineering,Jiangsu University,Zhenjiang,Jiangsu 212013,China
4.School of Food and Biological Engineering,Jiangsu University,Zhenjiang,Jiangsu 212013,China

A Fast Generalized Noise Clustering（FGNC）based on Generalized Noise Clustering（GNC）objective function and Possibilistic Clustering Algorithm（PCA）is proposed to deal with the shortcoming of GNC algorithm depend heavily on parameters, and FCM must be performed until termination to calculate the parameters for GNC algorithm.With a nonparametric method, FGNC calculates the parameters in GNC objective function.So FGNC algorithm does not depend on the parameters that GNC holds and clusters data faster than GNC algorithm.Experiment and simulation on two man-made data sets and two real data sets show FGNC can deal with noisy data well,cluster centers are closer to real ones,clustering accuracy is improved and clustering time is reduced.

Fuzzy C-Means（FCM）;Possibilistic C-Means（PCM）;Generalized Noise Clustering（GNC）

为解决广义噪声聚类（GNC）算法非常依赖参数和在运行GNC算法前必须运行FCM算法以便计算参数的缺点，在GNC的目标函数和可能聚类算法（PCA）基础上，提出一种快速的广义噪声聚类（FGNC）算法。FGNC算法通过一种非参数化方法计算GNC目标函数中的参数，因而FGNC算法不依赖参数并且聚类速度快于GNC算法。对人工含噪声数据集和两个实际数据集进行仿真实验，实验结果表明FGNC算法能很好地处理含噪声数据，具有聚类中心更接近真实聚类中心，聚类准确性高，聚类时间少的优良性能。

模糊C-均值聚类；可能C-均值聚类；广义噪声聚类

A

TP181

10.3778/j.issn.1002-8331.1112-0635

WU Bin,WU Xiaohong,JIA Hongwen.Fast generalized noise clustering algorithm.Computer Engineering and Applications,2013,49（13）：145-148.

安徽省高校省级优秀青年人才基金（No.2012SQRL251）；安徽省高校省级科学研究项目（No.KJ2012Z302）。

武斌（1978—），男，讲师，主要研究领域为模式识别和嵌入式系统工程；武小红（1971—），男，副教授，主要研究领域为模式识别和图像处理等；贾红雯（1978—），女，讲师，主要研究领域为通信和软件技术。E-mail：wubind2003@163.com

2012-01-09

2012-03-29

1002-8331（2013）13-0145-04

CNKI出版日期：2012-05-21http://www.cnki.net/kcms/detail/11.2127.TP.20120521.1137.003.html