改进的频域内亚像素级旋转角估计方法

张永亮，刘哲，郝珉慧，张鹤妮

西北工业大学 理学院，西安 710129

改进的频域内亚像素级旋转角估计方法

张永亮，刘哲，郝珉慧，张鹤妮

西北工业大学 理学院，西安 710129

1 引言

由于高分辨率具有更多关键的细节信息，因而人们期望获得高分辨率图像。依靠提高图像传感器分辨率的方法获得高分辨率图像，会受到硬件条件和经济成本的限制。一种具有应用前景的解决方法是运用超分辨率重构技术。超分辨率重构是指采用信号处理技术通过多帧低分辨率图像（Low-Resolution，LR）获得一帧高分辨率图像（High-Resolution，HR），即将针对同一场景的、彼此含有不同信息的、多帧低分辨率图像合成为一帧高分辨率图像。Borman[1]和Park[2]等概述了超分辨率图像重构算法。

超分辨率重构一般包括图像配准（参数估计）、图像重构两个步骤。图像配准的精度一般要求到达亚像素级。其中运动参数估计一般包括平移参数估计（shift estimation）和旋转角参数估计（rotation estimation）。如果运动参数估计误差较大，重构的高分辨率图像的质量会严重下降。因此，精确的亚像素级运动参数估计对于整个超分辨率重构算法是至关重要的。

研究者在图像亚像素配准方面已经做了很多工作，提出了很多配准算法[3-5]。Keren等提出了空域内亚像素级运动参数估计方法[6]；Reddy和Kim等提出了频域内亚像素级运动参数估计方法[7-9]；Vandewalle等提出了频域内运动参数估计的方法，配准的精度和时间效率较空域内的方法有明显的提高[10]，并且验证了该方法的鲁棒性。

但是，基于频域的旋转角估计的方法在旋转角比较小（比如小于1°）时，估计的误差往往较大。这是由于传统的方法主要利用了幅值很大的低频部分来计算相关性，而当旋转角度较小时，参与运算的低频部分幅值近似相等，无法估计出其中的不同，造成了旋转角估计的不准确。已有的改进算法由于低频部分较高的幅值，干扰了旋转角估计的准确性；同时考虑到高频部分的对噪声敏感，也会干扰到配准的准确性。综合考虑这两方面，本文用介于高频和低频之间的部分参与运算，提出了一种用局部频域幅值计算的改进方法。

2 频域内旋转角估计理论基础

用于超分辨率图像重构的低分辨率图像之间会由于传感器抖动，焦距变化而存在偏移。这种偏移一般来说是微小的，且一般只考虑平移和旋转两种参数。为叙述方便，本文只讨论两幅图像的旋转角估计算法，多幅图像的情况可类似得到。设图像水平平移参数为Δx1，垂直方向平移参数为Δx2，旋转角为ϕ，则待配准图像f1(x)、 f2(x)之间存在以下关系：

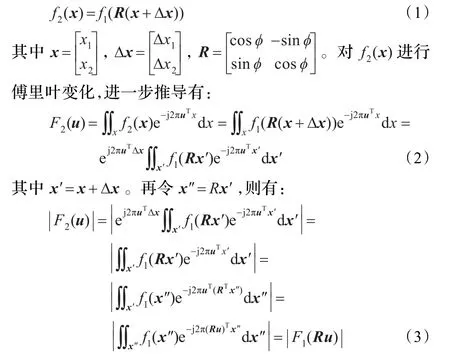
上式表明，待配准图像f1(x)、 f2(x)之间的旋转角与|F1(u)|、|F2(u)|之间的旋转角相等。因此，问题转化为如何准确估计|F1(u)|与|F2(u)|之间的旋转角，本文的旋转角估计算法是基于该结论的。

3 改进的频域内旋转角估计算法

图像配准中一种常用的方法是计算两幅图像的相关性，相关性最大时的参数即为最佳估计。直接计算两幅图像的相关性是二维问题，计算量很大，导致算法的时间效率很低。文献[10]提出了将二维问题转化为一维问题的算法，算法如下。

对待配准图像f1(x)、 f2(x)做傅里叶变化，求出|F1(u)|、|F2(u)|之后，将其从直角坐标系变化到极坐标系下，记为|F1(r，θ)|，|F2(r，θ)|。那么|F1(u)|与|F2(u)|之间的旋转角估计在极坐标下表现为|F1(r，θ)|与|F2(r，θ)|关于参数θ的平移估计。

定义函数hi(α)：

由于|Fi(r，θ)| ( i=1，2)是离散的，因此上述积分在计算中表现为累加的和的形式。函数hi(α)的实质是将|Fi(r，θ)|分为圆心角相等的若干个扇形，计算每个扇形区域内|Fi(r，θ)|的所有值之和。每个扇形的圆心角取为0.1°。为保证每个扇形区域内参与计算的点的个数相等，通常取r＜ρ（其中ρ是图像大小的一半）。图像的低频部分相对其他部分的值非常大，但是在将图像从直角坐标系变化到极坐标系下时，低频部分坐标的舍入误差较大，因此，r的下限取为r＞0.1ρ。

当计算出hi(α)之后，只要计算出一维序列h1(α)，h2(α)(α= 1,2,…，3 600)相关性最大的点，即可对应的计算出旋转角。

上述算法相对传统的算法时间效率高，精确度高，是一种有效的算法，但是进一步的实验结果表明，当待配准图像f1(x)、 f2(x)之间的旋转角较小时，上述算法往往不再有效，不能估计出准确的旋转角。分析其原因，是由于上述算法主要利用了图像的低频部分，但是低频部分相对高频部分的幅值很大，当旋转角过小的时候相邻的两个小扇形区域中的幅值之和近似相等，无法估计出其中的不同，因此当旋转角较小的时候，上述算法估计出的旋转角总为0。

一种有效的改进算法是只利用图像幅值相对较小的部分进行配准。高频部分相对低频部分的幅值很小，即使在旋转角较小时，也能估计出其中的不同，但是高频部分对噪声敏感，只用高频部分进行计算，算法的鲁棒性差；幅值很大的低频部分会干扰旋转角估计的精度；综合考虑这两方面因素，将调整r的取值范围为：aρ＜r＜bρ，求hi(α)时调整为计算α-Δα/2＜θ＜α+Δα/2，aρ＜r＜bρ区域内的幅值之和。其中a，b∈(0，1)，a＜b，且a＞0.1。即只选取频谱图的中间部分（以频谱图中心为圆心，以aρ、bρ为半径的两个圆环所围成的区域）参与运算。a、b的选取要根据重构的效果进行合适的调整。这种改进方法在保证算法鲁棒性的同时，提高了算法的精度。

在对待配准图像进行傅里叶变化之前，需要对其进行预处理，图像在进行傅里叶变化时由于图像边界不连续性会导致频谱中增加一个高幅值的“+”形特征。如图1所示，此特征会干扰配准结果，为此，在傅里叶变化之前，要用Tukey窗函数来消除该特征。

图1 “+”形噪声示意图

改进的旋转角估计算法步骤如下：

（2）对f1(x)、f2(x)分别进行傅里叶变化，并计算出

（3）将|F1(u)|和|F2(u)|变化到极坐标下，得到|F1(r，θ)|和|F2(r，θ)|。

（4）取α=0，1，…，3 599，对于每一个α，利用式（4）计算aρ＜r＜bρ，α·0.1°＜θ＜(α+1)·0.1°区域内的|F1(r，θ)|、|F2(r，θ)|之和，记为h1(α)、h2(α)，得到长度为3 600的序列h1(α)、h2(α)。

（5）计算出序列h1(α)、h2(α)相关性最大时的α的值α0，那么两幅图像之间的旋转角为0.1α0。

4 实验结果及分析

为了验证改进算法的有效性，选取512×512的两组图像Boat和Lena进行实验，并与传统的频域内旋转角估计算法进行了比较。其中待配准的图像是在原图像Boat和Lena的基础上旋转得到的。在用Boat图像进行实验时，选取参数a=0.6，b=0.8，实验结果见表1；用Lena图像进行实验时，选取参数a=0.3，b=0.8，实验结果见表2。

Boat图像的频谱图在某几个方向上能量比较高（频谱图中的亮线，见图2），因此其对应序列h1(α)和h2(α)有变化剧烈的局部峰值（见图3）；而Lena图像的能量在各个方向上分布相对均匀（见图1），对应的h1(α)和h2(α)序列的值变化缓慢。因此在选择参数a、b时，对于Boat图像，选取a=0.6，b=0.8的较小区间，即可估计出序列h1(α)和h2(α)相关性最大的点。而对于Lena图像，要选取一个更大的区间a=0.3，b=0.8，获取更多的信息，才能准确估计序列h1(α)和h2(α)相关性最大的点。

图2中，（a）、（c）之间的旋转角为1.35°，（b）、（d）为Tukey窗函数作用后对应图像的频谱图。视觉上可以看出，两者的频谱图之间存在一个旋转角度的差别。图3为从图2（b）、（d）中计算得到的h1(α)和h2(α)序列。两个序列之间存在14个单位的平移。因此，这种情况下，旋转估计值为1.4°。

图2 待配准图像及其频谱图

表1、表2的实验结果表明，对于小角度的旋转角估计，本文改进算法比传统算法更为有效；对于较大角度的旋转角估计，两者的效果相当。这就说明了本文算法的有效性。

5 总结与展望

亚像素级图像配准是超分辨率重构的重要步骤，配准的误差大将影响重构的效果。本文针对传统算法中对小角度估计不准确的缺点，提出了改进算法，并通过数据实验证明了算法的有效性。

表1 Boat组图像旋转角估计结果（°）

表2 Lena组图像旋转角估计结果（°）

图3 序列h1(α)和h2(α)

[1]Borman S，Stevenson R L.Spatial resolution enhancement of low-resolutionimagesequences—acomprehensivereview with directions for future research[R].Laboratory for Image andSignal Analysis（LISA），UniversityofNotreDame，Notre Dame，Ind，USA，1998.

[2]Park S C，Park M K，Kang M G.Super-resolution image reconstruction：a technical overview[J].IEEE Signal Processing Magazine，2003，20（3）：21-36.

[3]Schultz R R，Meng L，Stevenson R L.Subpixel motion estimation for super-resolution image sequence enhancement[J]. JournalofVisualCommunicationandImageRepresentation，1998，9（1）：38-50.

[4]Irani M，Peleg S.Improving resolution by image registration[J]. CVGIP：Graphical Models and Image Processing，1991，53（3）：231-239.

[5]Zitov´aB，Flusser J.Image registration methods：a survey[J]. Image and Vision Computing，2003，21（11）：977-1000.

[6]Keren D，Peleg S，Brada R.Image sequence enhancement using sub-pixel displacements[C]//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition，June 1988：742-746.

[7]Reddy B S，Chatterji B N.An FFT-based technique for translation，rotation，and scale-invariant image registration[J].IEEE Transactions on Image Processing，1996，5（8）：1266-1271.

[8]Kim S P，Su W Y.Subpixel accuracy image registration by spectrum cancellation[C]//Proceedings of IEEE International Conference Acoustics，Speech，Signal Processing（ICASSP’93），April 1993：153-156.

[9]Stone H S，Orchard M T，Chang E C.A fast direct Fourierbased algorithm for subpixel registration of images[J].IEEE Transactions on Geosciences and Remote Sensing，2001，39（10）：2235-2243.

[10]Vandewalle P，Süsstrunk S，Vetterli M.A frequency domain approach to registration of aliased images with application to super-resolution[J].EURASIP Journal on Applied Signal Processing，2005（5）：1-13.

ZHANG Yongliang,LIU Zhe,HAO Minhui,ZHANG Heni

School of Science,Northwestern Polytechnical University,Xi’an 710129,China

Sub-pixel image registration is an essential part of super-resolution image reconstruction algorithms.Unfortunately, when the rotation angel between input images is small,the conventional frequency domain algorithms cannot obtain an accurate estimation.Thus,an improved approach is proposed by taking into account both the high frequency and low frequency coefficients.The numerical results show that the proposed algorithm has a better performance in estimating the small rotation angles.

super resolution;frequency domain;rotation estimation;spectrogram

亚像素级配准是超分辨率重构的前提，其中旋转角估计的准确程度对重构效果有直接影响。针对传统的频域内旋转角估计在小角度估计不精确的缺点，提出了用部分幅值进行配准的改进算法。实验结果表明，改进算法对小角度旋转角估计比传统算法效果好。

超分辨率重构；频域；旋转角估计；频谱图

A

TP391

10.3778/j.issn.1002-8331.1111-0085

ZHANG Yongliang,LIU Zhe,HAO Minhui,et al.Improved frequency domain approach for rotation angle estimation. Computer Engineering and Applications,2013,49（13）：125-127.

国家自然科学基金（No.61071170）；教育部新世纪优秀人才支持计划。

张永亮（1988—），男，研究生，主要研究方向：图像重构，压缩传感；刘哲（1970—），女，博士，教授，主要研究方向：图像处理，压缩传感，信息融合与计算智能等。E-mail：zz_master@163.com

2011-11-11

2012-01-02

1002-8331（2013）13-0125-03

CNKI出版日期：2012-04-25http://www.cnki.net/kcms/detail/11.2127.TP.20120425.1722.080.html