选择分块SVM电容层析成像改进方法

李岩，袁小花，刘精松，柳培新，郑洁琼，张迪

哈尔滨理工大学 计算机学院，哈尔滨 150080

选择分块SVM电容层析成像改进方法

李岩，袁小花，刘精松，柳培新，郑洁琼，张迪

哈尔滨理工大学 计算机学院，哈尔滨 150080

1 引言

电容层析成像（ECT）技术是20世纪80年代后期形成和发展起来的，具有非侵入，结构简单，成本低，响应速度快，安全性能好和适用范围广等优点[1]。但由于受到独立电容测量值少，系统敏感场的“软场”特性及待解问题的非线性等因素的限制，给ECT系统图像重建算法的求解过程带来了一定的困难[2]，距离工业应用的要求比较远，因此研究良好的图像重建算法重要而迫切。支持向量机（SVM）作为机器学习的一个热点领域，由于它的可靠性和良好的推广能力，以及在多层次前馈神经网络领域被证明的优异性能，得到广泛的应用，也为ECT系统的图像重建提供了有力手段[3]。但目前在SVM的应用中还存在一些问题，如对不同的应用问题核函数参数的选择较难，对较复杂问题其分类精度不是很高以及对大规模分类问题训练时间长等。本文针对SVM在图像重建的大规模样本问题中训练时间长以及精度低的问题，提出了选择分块的SVM算法[4-6]应用到电容层析成像。如果样本数小到一定数据矩阵行的阈值，直接用SVM分类器；如果样本数超过数据矩阵行的阈值，则用CSSVM算法，针对一小块，从大样本中选择最适合这一小块的小样本组合，训练得到最佳模型。算法将大样本问题转变成小样本分类问题，降低了问题难度，使预测时间短，精度高。实验结果表明，CSSVM算法比单独使用SVM算法在重建图像时，具有更高的分类准确率和更短的成像时间。

2 基于SVM的图像重建原理

2.1 ECT系统传感器数学模型及电容求解

电容传感器的结构是在管道周围均匀排列12个电容极板，形成传感器阵列[7-9]。管道中流体流动状态的变化会引起电容传感器不同极板间的电容值的改变，所以要通过测量不同极板间的电容值，按照一定的成像算法就可以得到管道界面的流体流动情况。

对于任意两极板间的电容，用下式表示：

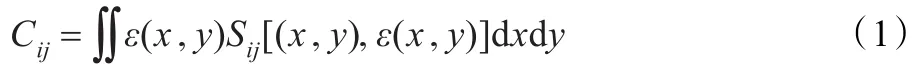
式中，Cij为电极i和j之间的内容值；ε(x，y)为介电常数分布函数，测量敏感区分布函数为Sij[(x，y)，ε(x，y)]。

2.2 支持向量机

ECT系统求解的样本集矩阵的列由66个电容值和66个敏感度值构成，它是一个非线性训练集。通过一个非线性映射，把样本空间映射到高维特征空间，在特征空间中应用线性支持向量机方法，解决样本空间的高度非线性分类问题。在高维特征空间构造一个最优分类超平面[10]。

非线性原问题表示为：

ϕ(xi)表示将样本xi从输入空间映射到高维特征空间；ω和b为待定的超平面参数，分别表示权值向量和偏置向量；c＞0为对于分类样本的惩罚参数；ξi为解决非线性不可分情况引入的松弛变量[11-13]。式（2）可以转化为对偶问题：

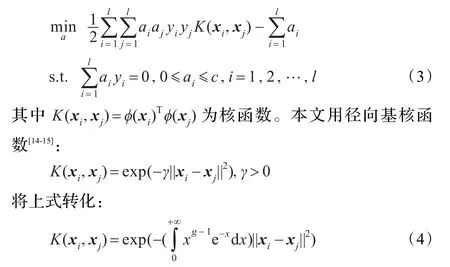
其中g为gamma核函数参数，g＞0为正数。代入式（3）求得最优超平面参数ω，偏置向量b0和Lagrange乘子a*。

最后SVM的判别决策函数为：

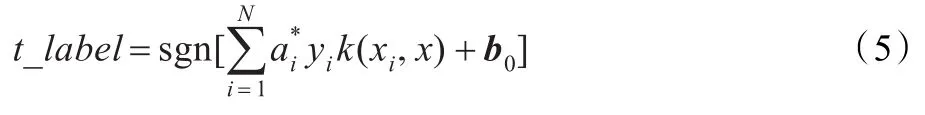
其中，t_label为成像单元的决策结果；xi为通过有限元软件计算得到的训练集数据（即ECT电容值和敏感度值），其值在训练前已被归一化。通过式（3）求得lagrange乘子和最优分类超平面的偏置向量b0，yi∈(-1，+1)为训练样本标签。通过式（4）求得径向基核函数k(xi，x)。

3 CSSVM算法的实现

3.1 数据预处理

本文实验中样本数据的指数取值范围为[1.0E－13，1.0E－4]，为提高实验训练及预测精度，将数据值归一化。

设数据矩阵为{x1，x2，…，xl}T，属性个数为q，则，建立映射f：

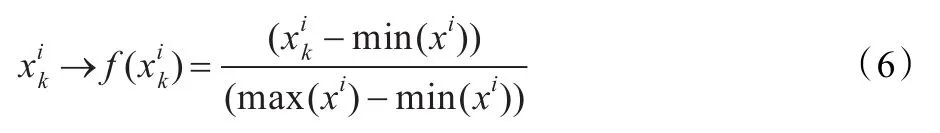
3.2 CSSVM算法实现

CSSVM算法规定，SVM算法处理的最大矩阵为200× 132矩阵，即矩阵行数阈值为200。

步骤1首先根据管道流体的不同流型选择典型样本数据。

（1）若将管道截面剖分为4个扇形单元，单元编号为1、2、3、4，4个单元水油分布组合为16种。对于1单元为水，其组合为1，12，13，14，123，124，134，1234，去掉通过单元旋转可以得到的重复样本14，134，124；对于1单元为油，其组合为2，3，4，23，24，34，234，全油，去掉通过单元旋转可以得到的重复样本3，4，34。实验选择的最小样本数为10，但实验中样本数选为16。

（2）若将管道截面剖分为r个扇形单元，其中r为8和16，并给每个单元编号。管道截面r个单元水油分布组合为2r，即可以有2r个样本，去掉通过单元旋转可以得到的重复样本，实验选择的样本个数为：

（3）如果管道按32剖分，即将管道截面分成8个扇形，去掉重复样本有34×2种组合，每个扇形再分成4份，共有16种组合，所以实验选择的样本个数为：

将上述的样本构造L×132的训练样本矩阵，其中L为样本个数或矩阵行数。

步骤2如果L≤200，转入步骤4。

步骤3如果L＞200，对模型分块并且标号，设初始成像单元号r=1，最大成像单元号为P，对每一个成像单元r，将它映射到可旋转重复的最小单元rmin，从原始L×132的样本矩阵中取出rmin单元标签为1的所有组合样本数m，再从其余里取出rmin单元标签为0的m个样本，重新组合成P个2m×132的训练数据矩阵。转入步骤4。

步骤4判断所有成像单元是否处理完毕。如果r＞P，训练结束，转入预测步骤6；否则用SVM算法训练训练样本集，选择惩罚参数c和核函数g。由式（4）径向基核函数公式将样本空间映射到高维特征空间，再代入公式（3）得到原问题最优解a*和b0，训练结束得到最佳训练模型。

步骤5r=r+1，转入步骤4。

步骤6将P个单元的训练模型代入式（5），并预测所有单元的结果，得到由P个值组成的一维向量，再重建图像。把式（5）预测得到的单元结果再分别代入式（8），得到单元的预测误差。

第r个单元的预测误差Ar定义为：

其中，r为1，2，…，P，yi∈{-1，+1}为第i个样本的实际值，Zi∈{-1，+1}为第i个样本的预测值。图像成像平均误差为：

4 实验结果及分析

实验采用ANSYS10.0软件，建立12电极传感器模型，模型剖分如图1所示。管道截面4均分时，由于仅有16组样本，保留重复样本。根据式（1），采用ANSYS的CMATRIX宏和ADPL语言编程求解出16组样本，每组样本有66个电容值[16]。管道16均分时，按公式（7）理论应求解4 099组非重复样本，但实验抽取求解了1 120组样本；32均分时实验求解了1 088组样本。

图1 ECT剖分图

本文做了3组实验。一组是将管道4均分，用SVM算法重建图像；第二组将管道16均分，用SVM算法训练重建图像和用CSSVM算法重建图像；第三组是将管道分成32均等分，应用CSSVM算法重建图像。

对管道内4均分时，训练数据矩阵为16×132，属于小样本训练，调整参数值直到训练精度达到最高100%；预测时间平均为0.050 8 s。

对管道内16均分时，训练数据矩阵为1 120×132，预测结果如表1所示。

表1 16均分管道SVM算法误差与时间

从表1可知16均分管道，将实验求解的数据直接用SVM算法，重建图像准确率低，耗时很大。再细分管道时，实验数据矩阵更庞大，占用内存更多。

16均分管道用CSSVM算法，针对一个单元选择数据矩阵138×132，调整单个的惩罚参数c和核参数g，直到误差达到最低。

实验结果如表2所示，对每一个成像单元选择样本组。

从表2可以看出，每个单元对应的最佳参数是不一样的；计算每个单元误差，得到平均误差为0.053 0。

将管道流体32均分并且标号，用CSSVM算法，针对每个单元选择164×132的训练数据矩阵，然后对数据预处理。参数的变化对训练矩阵的训练误差影响，如2号单元训练核函数参数g的选择与训练结果，见表3，训练误差是将训练集作为预测集预测得到的误差。

表2 16均分管道单元预测结果

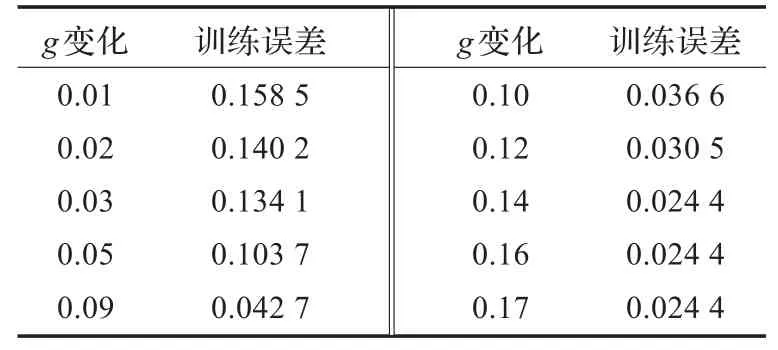
表3 核参数g对单元训练结果影响

针对2号单元的数据矩阵，核参数对其训练精度的影响，如图2所示。

2号单元训练精度随核参数g的增大而增加，但精度达到0.97时就稳定了，不再上升。实验选择使精度达到稳定的最小核参数g=0.14。

当均分为16单元或32单元时，对每个单元采用的核参数g进行训练，选择使精度达到最高的最小核参数值，得到如图3所示的单元对应最优核参数曲线图。

将管道截面平均分为4单元、16单元、32单元，再根据预测数组重建图像，结果如表4所示。

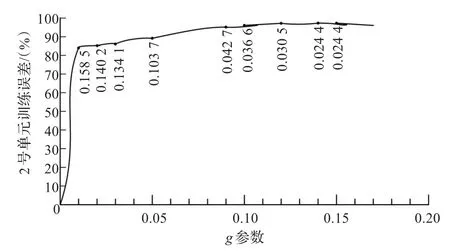
图2 g参数对精度的影响

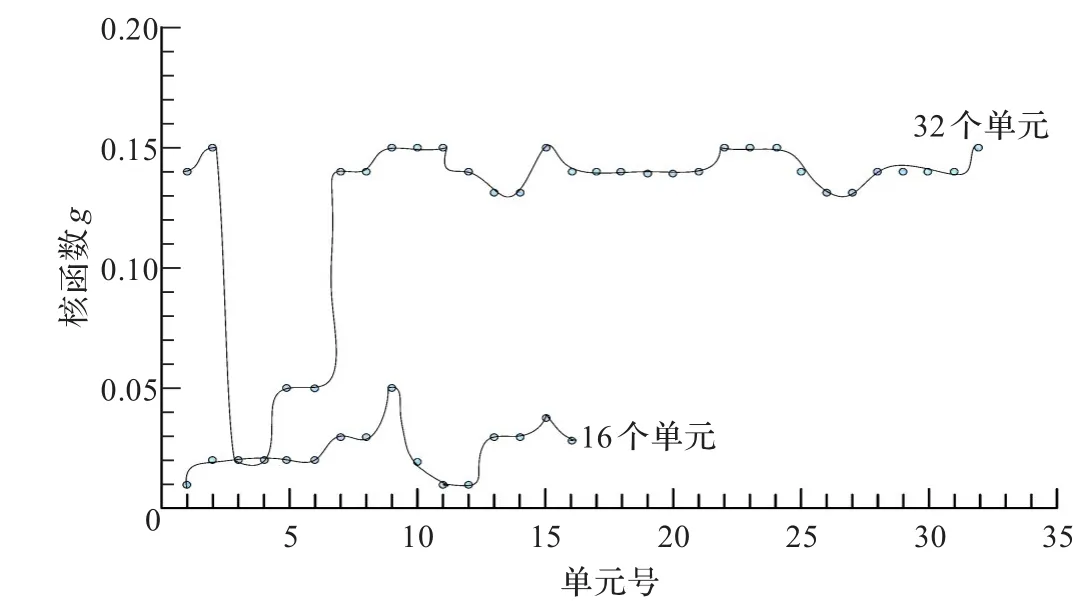
图3 单元对应的核参数曲线图

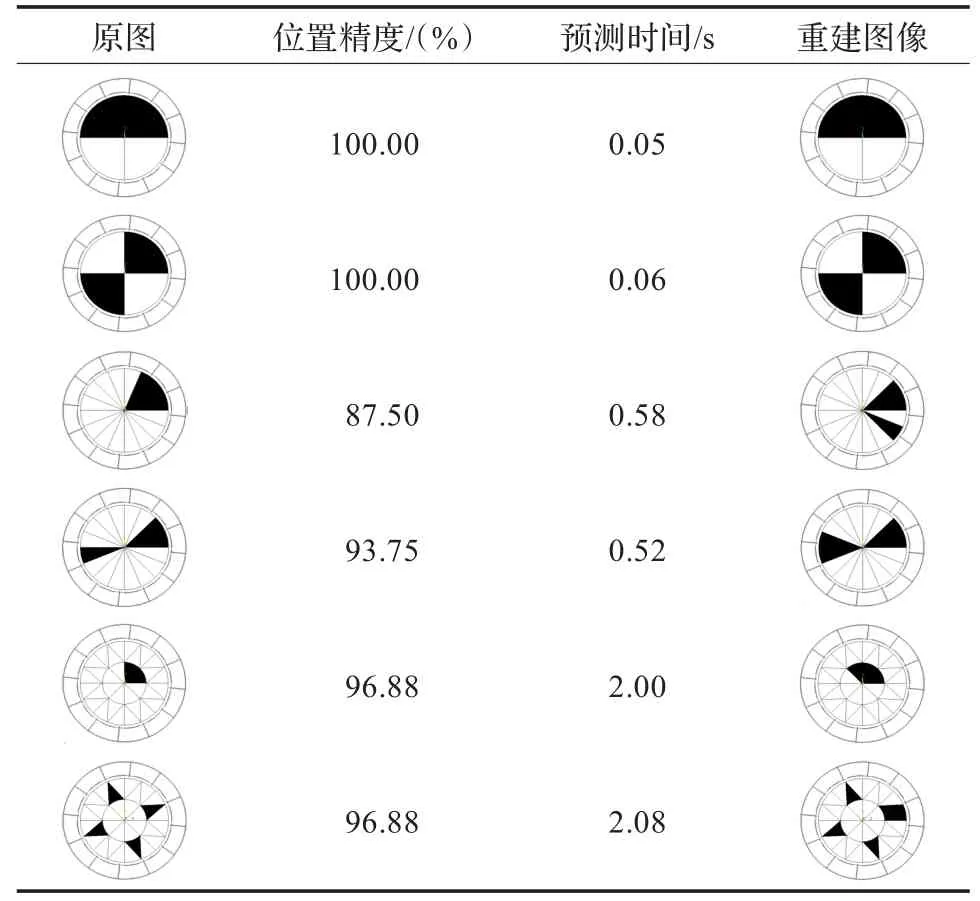
表4 重建图像

从实验数据可以得出，对管道4均分时，样本数少，样本数据矩阵规模小，直接用SVM分类器分类，重建图像快，精度高。如果对管道细分，将管道分成16份或32份时，采用CSSVM算法重建图像精度高，速度快。由上述实验推广到管道再细分情况，如管道64均分、192均分，采用CSSVM算法重建图像，能收到很好的效果。

5 结论

针对SVM在处理具有样本集规模大的ECT系统数据时，精度较低，训练时间较长的问题，采用CSSVM图像重建算法。将大规模数据矩阵，有选择地抽取块，降低了问题难度，并选择训练精度达到稳定的最优核参数。使用CSSVM算法重建图像准确率比单纯使用SVM算法有一定程度的提高，并且在大规模问题上，预测时间也减短很多。在今后的工作中，将引入硬件FPGA，用硬件实现图像重建的更高精度和更短时间。

[1]Neumayer M，Zang H，Watzenig D.Current reconstruction algorithms in electrical capacitance tomography[J].Lecture Notes in Electrical Engineering，2011，83：65-106.

[2]Fang W，Cumberbatch E.Matrix properties of data from electrical capacitance tomography[J].Journal of Engineering Mathematics，2005，51（2）：127-146.

[3]Tuia D，Muñoz-Marí J，Kanevski M.Structured output SVM for remote sensing image classification[J].Journal of Signal Processing Systems，2010，35：213-235.

[4]吴翔，谭李，陆文凯，等.提高超大规模SVM训练计算速度的研究[J].模式识别与人工智能，2003，16（1）：46-49.

[5]Li Y，Qian Y.Intrusion detection based on support vector machine divided up by clusters[C]//Proceedings of the International Conference on Computational Intelligence and Industrial Application，2010，3：284-286.

[6]陈蓉，宋俊德.基于SVM分块回归分析的话务量预测模型[J].计算机应用，2008，28（9）：2230-2232.

[7]Lei J，Liu S.An image reconstruction algorithm based on the regularizedminimaxestimationforelectricalcapacitance tomography[J].Journal of Mathematical Imaging and Vision，2011，39（3）：269-291.

[8]Walavalkar L.Support vector learning for gender classification using audio and visual cues[J].International Journal of Pattern Recognition and Artificial Intelligence，2003，17（3）：417-439.

[9]郭红星，余胜生，周敬利，等.12电极电容层析成象系统电容敏感场的仿真计算[J].系统仿真学报，2000，12（2）：172-174.

[10]Tatsumi K，Kawachi R，Hayashida K.Multiobjective multiclass soft-Margin support vector machine and its solving technique based on Benson’s method[C]//Proceedings of the 6thInternationalConferenceonModelingDecisionsfor Artifical Intelligence，2009，5861：360-371.

[11]杨俊丽，刘田福.基于支持向量机的中国地鼠分类特征基因选取[J].计算机应用，2011，31（2）：584-586.

[12]王晶，卫金茂.一种改进的支持向量机及其在癌症诊断中的应用[J].计算机应用，2006，26（2）：508-511.

[13]李蓉，叶世伟，史忠植.SVM-KNN分类器——一种提高SVM分类精度的新方法[J].电子学报，2002，30（5）：745-748.

[14]Vanschoenwinkel B，Manderick B.Appropriate kernel functions forsupportvectormachinelearningwithsequencesof symbolic data[C]//Proceedings of the 1st International Conference on Deterministic and Statistical Methods in Machine Learning.Berlin，Heidelberg：Springer-Verlag，2005：256-280.

[15]Kohram M，Noor M.Composite kernels for support vector classification of hyper-spectrctral data[C]//Proceedings of the 7th Mexican International Conference on Artifical Intelligence，2008，5317：360-370.

[16]朱艳丹.电容层析成像系统传感器场域分析与计算[D].哈尔滨：哈尔滨理工大学，2011：8-14.

LI Yan,YUAN Xiaohua,LIU Jingsong,LIU Peixin,ZHENG Jieqiong,ZHANG Di

College of Computer Science and Technology,Harbin University of Science and Technology,Harbin 150080,China

According to Support Vector Machine（SVM）has low training speed and low accuracy to deal with large scale data in Electrical Capacitance Tomography（ECT）system,a new algorithm that combined SVM with the Choice and Segmentation（CS）is presented and it comes into being a new classifier.Data in ECT system composes a data matrix which is fixed matrix column componented of sixty-six capacitance values and sixty-six sensitivity,the samples as its rows.It divides block selectively from large scale samples for one imaging unit.The numerical experiments show that the mixed algorithm can not only improve the accuracy compared to sole SVM,but also shorten time in imaging.

Support Vector Machine（SVM）;Choice and Segmentation（CS）;Electrical Capacitance Tomography（ECT）;data preprocessing;image reconstruction

针对SVM在处理具有样本集规模大的ECT系统数据时，存在ECT图像重建的成像精度不高和速度慢的问题，采用了选择分块支持向量机CSSVM算法。将ECT系统样本数据构成列数固定的样本矩阵，每个样本作为样本矩阵的行，66个电容值和66个敏感度值作为矩阵的列。该算法将大样本矩阵按照某一成像单元进行选择性分块，并形成多个小样本矩阵，再分别采用SVM算法进行训练和预测，将各个成像单元组合成像。数值实验证明，使用CSSVM新算法比单独使用SVM算法重建图像具有更高的分类准确率和更短的成像时间。

支持向量机；选择分块；电容层析成像；数据预处理；图像重建

A

TP391.4

10.3778/j.issn.1002-8331.1111-0144

LI Yan,YUAN Xiaohua,LIU Jingsong,et al.Improved method of electrical capacitance tomography based on SVM algorithm of choice and segmentation.Computer Engineering and Applications,2013,49（13）：110-113.

国家自然科学基金（No.60572135）；黑龙江省自然科学基金（No.F200505）；黑龙江省教育厅基金（No.12521100）；研究生创新基金（No.HLGYCX2011-015）。

李岩（1966—），男，教授，研究生导师，主要研究方向：多相流检测，嵌入式系统，仪器仪表与计算机控制等；袁小花（1988—），女，硕士研究生。E-mail：yuanxiaohua2010@163.com

2011-11-14

2012-03-14

1002-8331（2013）13-0110-04

CNKI出版日期：2012-05-09http://www.cnki.net/kcms/detail/11.2127.TP.20120509.0845.002.html