利用多群交叉变异人工鱼群算法生成分类规则

戴上平，姬盈利，王华

1.华中师范大学 计算机科学系，武汉 430079

2.武汉大学 资源与环境科学学院，武汉 430079

利用多群交叉变异人工鱼群算法生成分类规则

戴上平1，姬盈利1，王华2

1.华中师范大学 计算机科学系，武汉 430079

2.武汉大学 资源与环境科学学院，武汉 430079

1 引言

人工鱼群算法是通过将需要解决的现实问题抽象为人工鱼，模仿鱼类底层的觅食、聚群、追尾等行为来实现寻优的群体智能优化算法[1-3]。该算法由于具有对初值、参数选择要求不高，对启发式函数不敏感，简单易实现，鲁棒性强等优点在函数优化、参数估计、模式识别、神经网络结构优化、分类预测等诸多领域得到了广泛应用[4-9]。

分类是数据挖掘领域研究的一个重要问题，其目的是通过分析数据集合，生成能够对数据进行区分的特征描述，从而对未知数据进行分类预测，它对指导人们解决现实生活的很多问题有重要意义。常用的分类方法有统计机器学习、决策树、神经网络、支持向量机、粗糙集、贝叶斯方法等[10-13]。

本文尝试将人工鱼群算法应用于解决分类问题，在对基本人工鱼群算法思想分析的基础上，引入交叉变异策略，构建了能够生成连续空间变量分类规则的多群交叉变异人工鱼群算法（Multi Artificial Fish Warm Algorithm with Cross and Mutation，MAFWA_CM）。与传统鱼群算法提取分类规则方法相比，本文利用多种群人工鱼群中的每一鱼群对应于一条规则的提取，其收敛速度更快，求解精度更高。并且由于多群人工鱼群在数据以及任务分割上的简便性，使其在将来算法的并行性实现上更为简单。最后，利用仿真实验证明了本文算法在连续变量空间内生成分类规则的可行性。与基本人工鱼群规则提取算法相比[14]，本文提出的MAFWA_CM算法具有更快的收敛速度并能获得较高的规则精度。此外，实验还给出了本文算法与多群体微粒群规则提取算法的结果比较分析。

2 基本人工鱼群算法

基本人工鱼群算法原理可参考文献[1-3]。本章重点介绍基本人工鱼群的相关参数定义以及几类基本行为。

2.1 人工鱼参数意义

拥挤度（ϑ）用来控制鱼群个体之间不会过分拥挤；步长（step）表示人工鱼每次移动的长度；距离（d(i，j)）表示两条人工鱼个体之间的距离；感知范围（visual）表示人工鱼的可视范围；试探次数（trynumber）表示人工鱼每次选择移动方向的最大试探次数。

2.2 人工鱼行为描述

假定人工鱼当前的状态表示形式为Fish(X1,X2,…，Xn,C)，计算食物浓度的适应值函数为y=f(x)，人工鱼迭代选择执行觅食行为、聚群行为、追尾行为中能使自身状态达到最优的一种行为来执行。在不断地比较判断更新自身状态的过程中，使得人工鱼的下一状态最优，每个人工鱼个体通过这样的方法局部寻优，最终使全局最优值在群体中突现出来。下面详细描述几种行为。

觅食行为：设定人工鱼当前状态为xi，在其邻域(d(i，j)＜visual)内随机选择另外一个状态xj，比较xi、xj处食物浓度的大小yi、yj，如果yi＜yj，则人工鱼向xj处前进一步；否则就再选择一个新的状态xj，重新进行食物浓度大小的比较。如果试探了trynumber次仍然找不到食物浓度比较大的点，就随机移动一步。

聚群行为：设定人工鱼当前状态为xi，在其邻域(d(i，j)＜visual)内搜索中心位置xc及伙伴数目nf，如果yc/nf＞ϑ×yi，则向伙伴中心位置随即移动一个步长；否则执行觅食行为。

追尾行为：设定人工鱼当前状态为xi，在其邻域(d(i，j)＜visual)内搜索食物浓度ymax最大的人工鱼xmax，如果ymax/nf＞ϑ×yi，则向xmax方向随机移动一个步长；否则执行觅食行为。

3 多群交叉变异人工鱼群分类规则提取算法

多群人工鱼群分类规则提取算法的特点是通过将数据与任务进行分割，每一个鱼群对应负责某一类数据特征的提取任务，多个鱼群并行计算，鱼群之间无需进行复杂的通信，在满足一定规则精度或者达到预先设定的迭代次数时，再将各鱼群提取的规则进行综合，便形成完整的置信度较高的用于分类预测的规则集合。在此算法基础上引入交叉变异算子，即为多群交叉变异人工鱼群分类规则提取算法。为实现多群交叉变异人工鱼群分类规则提取算法，需明确分类规则表达形式及评价、人工鱼构造、交叉变异算子设计三类问题。

3.1 规则表达形式及评价

3.1.1 规则表示形式

一般分类的规则表示形式为：

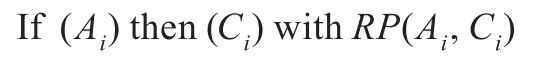
式中，规则前件Ai代表数据集的特征属性集合；规则后件Ci代表数据集类别；RP(Ai，Ci)代表隶属规则的优先级，用于解决某一个数据个体符合多项判别规则的问题。当某一个实例的特征属性集合与规则前件匹配，并且用该规则分类得出的实例类别与该实例所属的类别一致时候，就说明这个实例被正确分类。

3.1.2 分类规则评价

要提取到最优的规则，就要在训练过程中确定合适的适应度函数对规则进行评估。规则的支持度（support）和规则的可信度（confidence）是衡量规则好坏的两个重要指标，因此在确定适应度函数之前引入这两个指标的相关定义：

定义1（支持度）对于规则if(Ai)then(Ci)，如果某种群中有s%的个体满足规则即包含，Ai∪Ci则称该规则的支持度为s%，记为support(Ai)即：

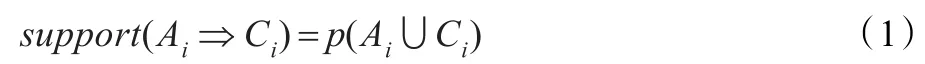
定义2（信任度）若规则if(Ai)then(Ci)的支持度为support(Ai)，则规则的信任度为support(Ai∪Ci)/support(Ai)记为：

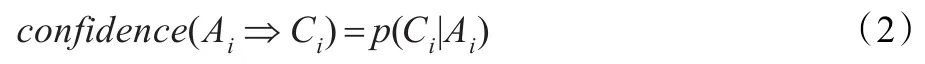
定义1说明规则的支持度及规则的普遍性反映了正确分类的个体数目占种群中个体总数的比例。规则的支持度度越高表明该规则能够将实例进行正确分类的数目越多。定义2说明规则的信任度即规则的准确度反映一条规则能将一个个体正确分类的概率。规则的信任度表明个体用该规则能够正确分类的概率大。因此确定适应度函数为：

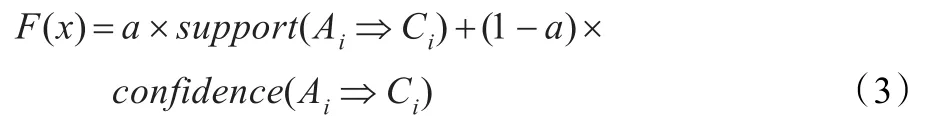
式（3）通过支持度和置信度来综合评估规则的质量。式中a为支持度系数，值域为（0，1），通过该系数保证生成的规则即能将大部分的样本正确分类，同时也有较高的概率能将单个样本正确分类，保证生成的规则向最优的方向发展。

3.2 人工鱼构造

为将人工鱼群用于连续空间变量的数据分类规则提取问题中，需要在基本人工鱼算法的基础上对人工鱼编码、人工鱼距离、人工鱼的邻居及聚类中心进行相关的定义。

3.2.1 人工鱼编码

本文算法中每条人工鱼代表一条候选规则，在算法实现中，对人工鱼的编码需要能够直观的表达规则。因此用Fish(X1，X2，…，Xn，C)这种编码形式来代表一条人工鱼，其中前n维的具体编码可以见表1，每一维均分别定义其特征上下界。第n+1维C代表类别属性。将其解码为规则表现形式：if X1_min＜X1＜X1_maxand X2_min＜X2＜X2_maxand…and Xn_min＜Xn＜Xn_maxthen C。

表1 人工鱼编码

3.2.2 人工鱼的相关概念

在算法的迭代进化过程中，人工鱼距离、邻域、聚群中心位置、食物浓度是几类非常重要的概念，本文定义了这四类概念在分类规则提取中的具体实现方式。

（1）人工鱼距离：人工鱼的距离表示两个规则之间的差异性，本文定义了基于欧几里得距离的人工鱼距离计算公式。例如，人工鱼Fishi和Fishj之间的距离可通过下式来计算：

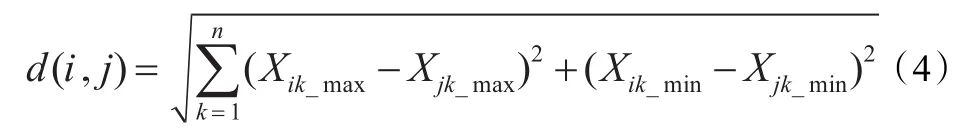
其中，n代表特征维数，Xik_max代表人工鱼i的第k个属性的上界，Xik_min代表人工鱼i的第k个属性的下界。

（2）邻域：在人工鱼距离的基础上定义人工鱼Fishi的邻域为：

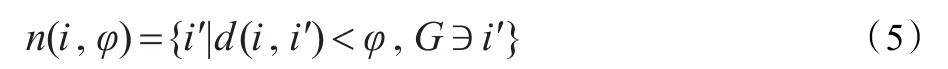
其中，i′代表邻域内其他个体，φ代表邻域距离，G代表整个鱼群。

（3）中心位置：一个人工鱼聚群的中心位置，在算法中分别取所有人工鱼的每一维特征值上下界的平均值。

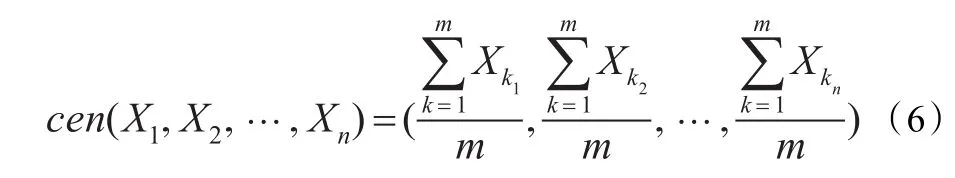
式中，m代表聚群中人工鱼个体数。

（4）食物浓度：食物浓度就表示规则质量，通过公式（3）进行计算。

3.3 交叉变异算子设计

当人工鱼群算法迭代进行到一定代数，算法容易陷入局部最优解，为了保持种群的多样性，更好地获得全局极值，针对MAFWA_CM算法的具体应用，设计了人工鱼规则编码的交叉变异算子。

（1）交叉算子

假定交叉概率为P_Cross，在一个种群中，随机选择P_Cross×m个人工鱼个体两两执行交叉操作。例如，选择人工鱼个体Fishi、Fishj，根据3.2.1小节人工鱼的编码规则，对两个人工鱼个体的前n维的上下界执行如公式（7）所示的交叉操作：

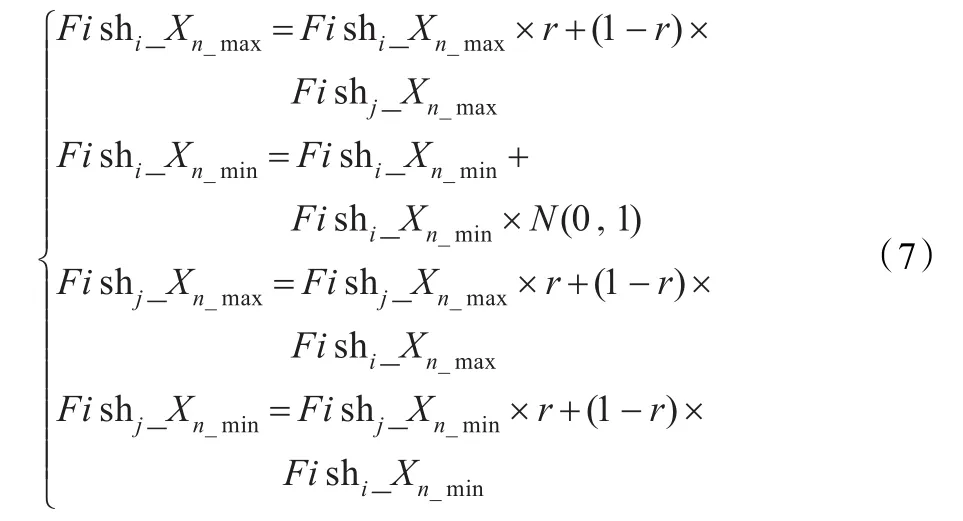
其中，r为每一维随机产生的范围为[0，1]之间的数字。

（2）变异算子

假定变异概率为P_Mutation，在一个种群中，随机选择P_Mutation×m个人工鱼个体执行变异操作。将选择出来的人工鱼个体Fishi执行如式（8）所示的高斯变异[15]：

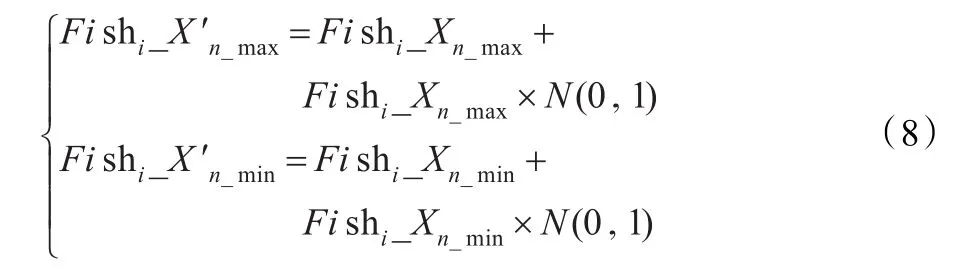
其中，Fishi_与Fishi_是变异后第i维特征属性的上下界值，N(0,1)为服从均值为0，方差为1的高斯分布随机变量。

3.4 算法的整体描述

在上述定义的基础上，本文算法的整体实现流程见图1。

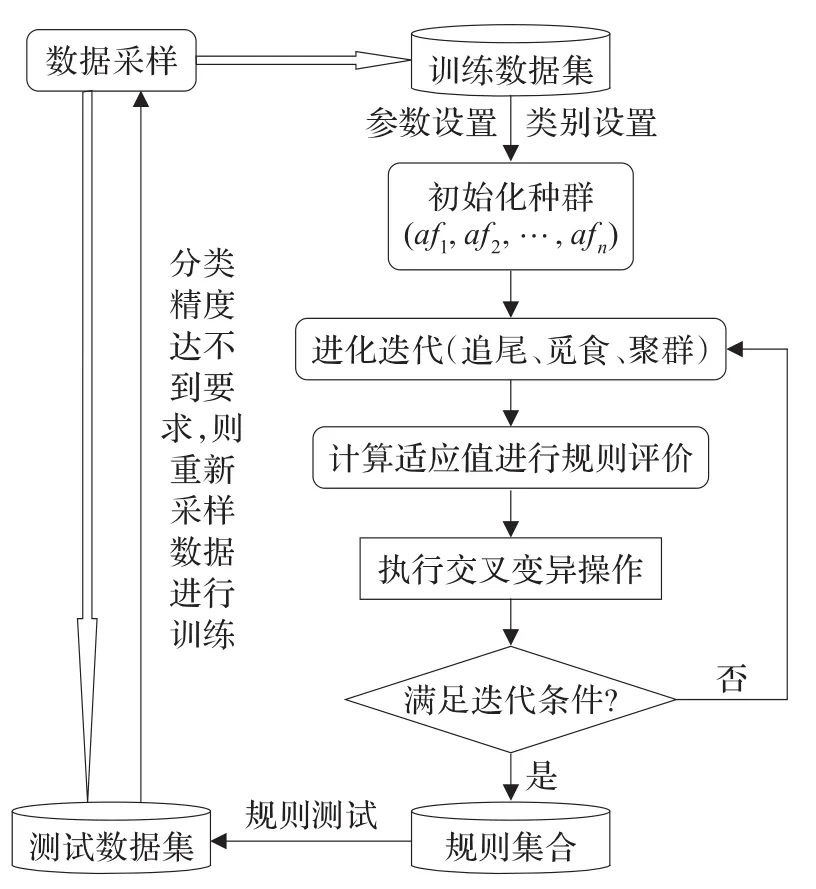
图1 MAFWA_CM分类规则提取算法流程图

步骤1通过数据采样将数据集分为训练数据集和测试数据集。

步骤2设置鱼群欲提取规则的类别及步长、可视范围等参数，根据3.2.1小节的人工鱼编码方式进行种群的初始化。

步骤3对鱼群，按公式（4）、（5）、（6）来进行觅食、追尾、聚群等行为。

步骤4根据公式（3）计算每一人工鱼的适应值，对规则质量进行评估，将最优个体放入公告板。

步骤5按公式（7）、（8）对种群执行交叉变异操作。

步骤6判断算法是否达到最大迭代次数或者连续几代公告板未发生变化，则认为达到算法终止条件执行步骤7；否则执行步骤3。

步骤7将生成的规则加入到规则集合中。

重复执行步骤1到步骤7直到找到较优规则。最后用测试数据集检验规则集合精度，如果不满足要求则重新进行步骤1。

4 实验仿真及分析

4.1 实验数据集

为验证算法的性能，采取来自UCI机器学习知识库中的Wine和Iris数据集来进行测试实验。植物数据集Iris由分别属于3种植物（setosa、versicolor、virginica）的150个样本组成，每个样本包含4个特征属性：花瓣长度、花瓣宽度、花萼长度、花萼宽度。Wine数据集包含178个样本，每个样本包含13个特属性，3个类别。如表2所示。

表2 UCI数据集

4.2 实验结果与分析

本文采用的是5折交叉验证法进行实验，用n%5的策略把数据分成5份，其中n为数据的记录号，即将行号除以5所得余数相等的数据归为一个子集，设为D1，D2，…，D5，训练和测试轮流进行5次，每一次训练都选用不同的数据集子作为测试集，其余的4个子集都用于训练集，取5次的平均值作为最终的实验结果。

本文算法的参数设置：最大迭代次数为50，单群人工鱼个数30，可视范围为2，步长为0.5，最大尝试次数是30，支持度系数为0.5，交叉概率0.3，变异概率0.01。其中，用本文提出算法对Iris数据集的提取规则结果如下：

为验证算法的改进效果，本文将基本多群体人工鱼群（MAFWA）分类规则提取算法与引入了交叉变异算子的MAFWA_CM算法进行了性能的对比分析。两类算法的主要参数设置一致，并且在相同数据集上进行测试，将结果进行比较。分类精度及计算时间结果如表3所示；以Iris数据集为例，绘制了两类算法在类别规则提取时的适应值收敛图，如图2所示。

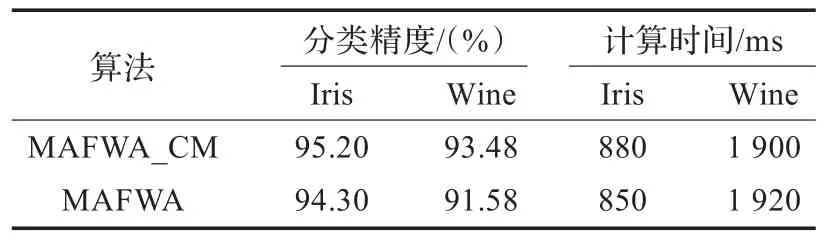
表3 MAFWA与MAFWA_CM算法分类结果对比

如表3，从分类精度上来看，MAFWA_CM在两类数据集上均优于MAFWA算法，其主要原因是交叉变异算子的引入能够有效提高种群多样性，具有更好的全局最优解的获取机制。在计算时间方面，MAFWA_CM算法在Iris数据集上要略逊于MAFWA，其主要原因是由于MAFWA_CM的交叉变异操作增加了时间复杂度，算子的时间开销超过了提前收敛（图2所示）所节省的时间；而其在Wine数据集上的计算时间则略优于MAFWA算法，说明在多维数据集上的快速收敛性能所节省的时间要多于交叉变异算子的时间开销。

由图2可以看出：在对规则1的生成中，本文提出的MAFWA_CM算法在第4代开始收敛，MAFWA算法则收敛于第6代；在规则2的生成中，虽然MAFWA_CM算法初始化时的群体最优适应值低于MAFWA算法，但是只经过1代的进化，最佳适应值就明显超过MAFWA算法，并且最终收敛于第7代，而MAFWA算法收敛于第9代，并且其最优适应值0.95略小于MAFWA_CM算法的0.97；在规则3的生成中，同样MAFWA_CM算法初始化时的群体最优适应值低于MAFWA算法，但是经过2代的进化，最佳适应值就明显超过MAFWA算法，并且最终收敛于第8代，其最佳适应值为0.94，略优于MAFWA算法的0.92，MAFWA算法则在第10代开始收敛。该结果直观地说明了MAFWA_CM算法的收敛性能优于MAFWA算法，交叉变异算子的引入是有效的。

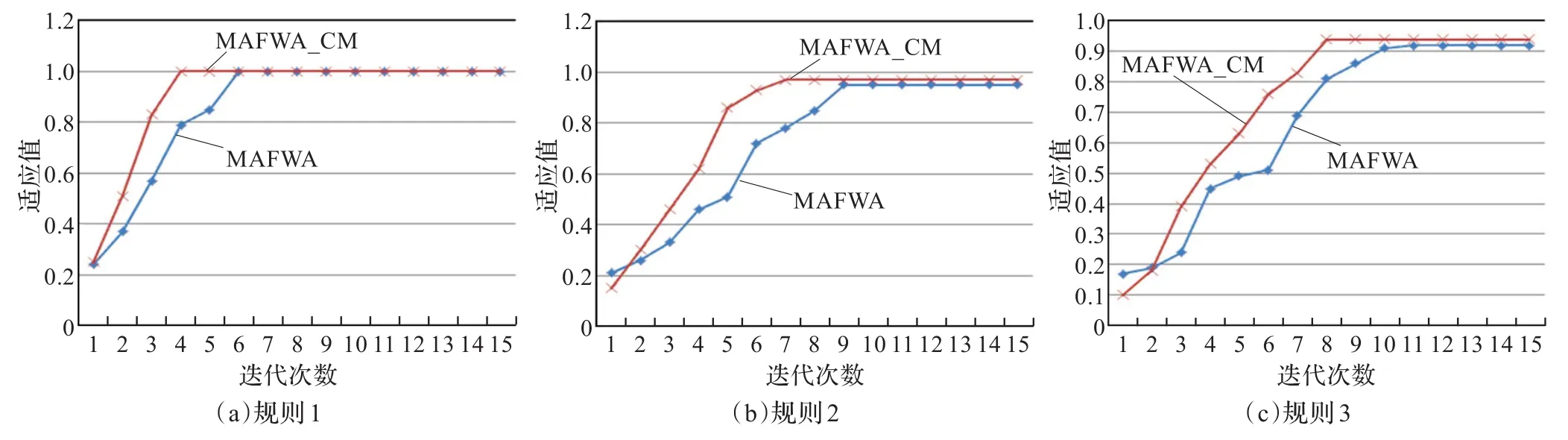
图2 MAFWA与MAFWA_CM算法收敛对比图

同时，本文还将分类结果与文献[16]中的多群体微粒群算法（MPSO）进行了比较，如表4所示。

表4 MAFWA、MAFWA_CM与MPSO算法分类结果对比

由表4可以看出，在分类精度上，Iris数据集上MAFWA算法的分类精度最低，但是较接近于MPSO算法。而MAFWA_CM算法的分类精度则要明显优于MPSO算法，在Wine数据集上，MAFWA算法的分类精度同样最低，而MAFWA_CM算法的分类精度略高于MPSO算法，说明引入了交叉变异算子的MAFWA_CM算法在对多维特征的数据集的搜索最优解的能力已达到MPSO算法的性能；在规则数目上，3种算法对Wine数据集均提取了4条规则，MAFWA与MAFWA_CM算法对Iris数据集提取了3条规则，而MPSO算法提取了5条规则，说明MAFWA与MAFWA_CM算法在低维数据集的学习能力上不逊于MPSO算法。

5 结论

实验结果表明，使用MAFWA_CM算法能够以较快的收敛速率生成具有较高精度和较少数目的分类规则。与MAFWA算法相比，本文算法在收敛速度和分类精度上全面优于MAFWA算法，但是在计算时间上，处理低维数据时由于交叉编译操作的时间开销超过了提前收敛所节省的时间，本文算法要逊于MAFWA算法；与MPSO算法相比，本文算法不仅在处理低维数据变量时规则的精度以及数目均明显优于MPSO算法，而且对多维特征数据集搜索全局最优解的能力与MPSO算法也基本相当。因此，本文MAFWA_CM算法在对连续变量空间分类规则提取问题中是可行并且有效的，尤其适用于解决高维连续空间变量的分类规则提取问题。

[1]李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式：鱼群算法[J].系统工程理论与实践，2002（11）：32-38.

[2]王联国，洪毅，赵付青，等.一种改进的人工鱼群算法[J].计算机工程，2008，34（19）：192-194.

[3]Yazdani D，Toosi A N，Meybodi M R.Fuzzy adaptive artificial fish swarm algorithm[C]//Proceedings of the 23rd Australasian Joint Conference on Artificial Intelligence，Adelaide，Australia，2010：334-343.

[4]黄华娟，周永权.改进型人工鱼群算法及复杂函数全局优化方法[J].广西师范大学学报，2008，26（1）：194-196.

[5]李晓磊，薛云灿，路飞，等.基于人工鱼群算法的参数估计方法[J].山东大学学报，2004，34（3）：86-87.

[6]Shen W，Guo X，Wu C.Forecasting stock indices using radial basis function neural networks optimized by artificial fish swarm algorithm[J].Knowledge-Based Systems，2011，24（3）：378-385.

[7]师彪，李郁侠，于新花，等.弹性自适应人工鱼群-BP神经网络模型及在短期电价预测中的应用[J].水力发电学报，2010，29（1）：107-113.

[8]Murak A K.Constrained parameter estimation with applications to blending operations[J].Journal of Process Control，2000，10（2）：195-202.

[9]刘双印.免疫人工鱼群神经网络的经济预测模型[J].计算机工程与应用，2009，45（29）：226-229.

[10]谢娟英，刘芳，冯德民.基于GA与RST的分类规则挖掘算法[J].计算机科学，2006，33（11）：149-156.

[11]Tsumoto S.Automated extract ion of hierarchical decision rules fromclinicaldatabasesusingroughsetmodel[J].Expert Systems with Applications，2003，24（2）：189-197.

[12]Roubos J A，Setnes M，Abonyi J.Learning fuzzy classification rules from labeled data[J].Inf Sci，2003，150（1/2）：77-93.

[13]覃俊，康立山，陈毓屏.用于分类规则提取的演化算法分析与设计[J].计算机工程与应用，2004，40（2）：13-15.

[14]陈俊清，朱文兴.基于人工鱼群算法的分类规则发现[J].福州大学学报，2007，35（1）：25-30.

[15]曲良东，何登旭.基于自适应高斯变异的人工鱼群算法[J].计算机工程，2009，35（15）.

[16]延丽平，曾建潮.利用多群体PSO算法生成分类规则[J].计算机工程与科学，2007，29（1）.

DAI Shangping1,JI Yingli1,WANG Hua2

1.Department of Computer Science,Central China Normal University,Wuhan 430079,China
2.School of Resource and Environment Science,Wuhan University,Wuhan 430079,China

The Multi Artificial Fish Warm Algorithm（MAFWA）based on the work principle of basic Artificial Fish Warm（AFW）is presented for extracting the classification rules of continuous variable.The code of artificial fish is designed in terms of the characteristics of extracting the classification rules.Then the fitness function to evaluate the quality of the regular rule is established and some formulas to calculate some key parameters for its application in extracting classification rules are defined. Meanwhile,in order to avoid the MAFWA falling in the local optima,the crossover operator and mutation operator of the AFW are designed based on the mutation and crossover idea of Genetic Algorithm（GA）.Then the MAFWA with Cross and Mutation（MAFWA_CM）is proposed.At last,the algorithm is tested on the Iris and Wine data sets.The experimental results show:（1）the algorithm can extract the classification rules with high precision in a short time.（2）When referred to the efficiency of the convergence and the precision of the rule,the MAFWA_CM is superior to the single AFW and is closer to the multi particle swarm algorithm.

Multi Artificial Fish Warm Algorithm（MAFWA）;Cross and Mutation（CM）;classification rule

在基本人工鱼群算法的基础之上构建了用于解决连续变量空间分类规则提取的多群体人工鱼群算法，根据分类规则提取问题的特性设计了人工鱼的编码规则，并在此编码基础上定义了进行规则评价的适应值函数以及相关状态更新公式。为克服人工鱼群算法易陷入局部最优解的缺陷，引入了遗传算法中的交叉变异思想，设计了基于人工鱼的交叉及变异算子，提出了利用多种群交叉变异人工鱼群算法生成分类规则的算法思想。利用Iris和Wine数据集作为测试数据，结果表明：（1）该算法能够快速生成精度较高的分类规则；（2）在收敛效率及规则精度上全面优于基本多群体人工鱼群算法，并达到了多群体微粒群算法的性能水平。

多群体人工鱼群；交叉变异；分类规则

A

TP301.6

10.3778/j.issn.1002-8331.1110-0657

DAI Shangping,JI Yingli,WANG Hua.Extracting classification rules by using multi artificial fish warm algorithm with cross and mutation.Computer Engineering and Applications,2013,49（13）：100-104.

国家高技术研究发展计划（863）（No.2011AA120304）。

戴上平（1961—），男，博士，副教授，研究领域为人工智能，数据挖掘；姬盈利，硕士研究生，研究领域为人工智能，数据挖掘；王华，博士研究生，研究领域为空间数据挖掘，智能地理计算。E-mail：lucky201199@163.com

2011-11-03

2012-01-02

1002-8331（2013）13-0100-05

CNKI出版日期：2012-03-21http://www.cnki.net/kcms/detail/11.2127.TP.20120321.1738.053.html