组合谱图法在跳频信号时频分析中的应用

曾祥峰，杨育红，崔鹏辉，温洲

1.信息工程大学 信息工程学院，郑州 450002

2.中国人民解放军65021部队

组合谱图法在跳频信号时频分析中的应用

曾祥峰1，杨育红1，崔鹏辉1，温洲2

1.信息工程大学 信息工程学院，郑州 450002

2.中国人民解放军65021部队

1 引言

跳频通信方式具有抗干扰、抗检测、安全性高等优点，在众多领域中得到了广泛应用。由于跳频信号是一种典型的非平稳信号，因此在其参数估计过程中，往往采用时频分析方法，而时频分析算法的性能直接影响了参数估计的准确性[1]。Potter等人[2]提出的短时傅里叶变换是一种常用的时频分析方法，其优点是算法复杂度低，无交叉项影响，缺点是时频分辨率低。1948年，Ville将Wigner提出的Wigner分布引入时频分析中，形成了著名的Wigner-Ville分布（WVD）[3]。WVD具有最好的时频分辨率，但是在处理复杂信号时存在严重的交叉项干扰问题。为了解决交叉项问题，国内外学者提出了伪维格纳-维尔分布（PWVD）[4]、平滑伪维格纳-维尔分布（SPWVD）[5]等方法，但是牺牲了分辨率且无法完全消除交叉项[6]。文献[7]提出一种基于信号分解的WVD算法对跳频信号进行分析，虽然避免了交叉项，但是硬件电路复杂，且需要一定的先验条件。1982年，Morlet提出了小波变换思想[8]；文献[9-10]采用了小波变换对跳频信号进行了分析，其缺点是对噪声敏感且需要一定的先验条件。

为了在避免交叉项的前提下，提高分辨率，本文利用了谱图法在分析跳频信号时交叉项为零的特点，采用组合窗对谱图法进行了改进，提高了原算法的分辨率和参数估计性能，并给出了理论分析和仿真结果。

2 信号模型

跳频信号的载频在不同频点上伪随机跳变，因此可以将跳频信号视为多个窄带信号的叠加：

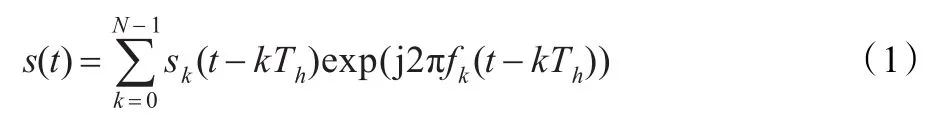
其中Th为跳频周期，fk为跳频频点，N-1为频点数量。

2.1 多信号维格纳-维尔分布

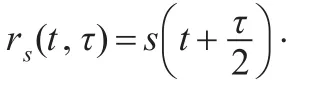
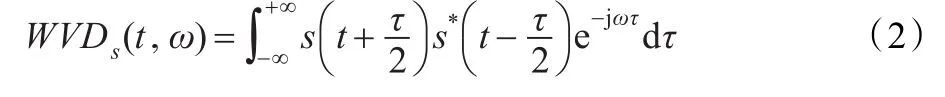
对于多个信号s(t)=s1(t)+s2(t)，维格纳-维尔分布可表示为：

其中，WVDs1(t，ω)和WVDs2(t，ω)分别为两个信号的维格纳-维尔分布，2Re[WVDs1，s2(t，ω)]为交叉项。若信号个数为N，交叉项数为N(N-1)/2。

2.2 多信号谱图法

谱图法定义为短时傅里叶变换模的平方，其表达式为：

其中，SPECs1(t，ω)和SPECs2(t，ω)分别为两个信号的谱图表示，而为谱图法中的交叉项，由两个子信号的短时傅里叶变换和一个余弦函数组成，θs1、θs2分别是信号s1(t)、s2(t)的短时傅里叶变换的相位。

3 基于谱图法的算法改进

从前文的分析可知，采用谱图法分析跳频信号时，不存在交叉项问题，但分辨率相对于维格纳-维尔分布还是不令人满意。本章将以提高谱图法的分辨率为目标，进行改进。

3.1 影响分辨率的因素

从频域上来看，谱图法中窗函数h(t)可以看做是一个低通滤波器的脉冲响应。窗函数时宽越窄，时间分辨率越高，但这时低通滤波器的通带就越宽，频率分辨率也就越低，反之亦然。时间和频率分辨率不可能同时很高，只能在两者间取折衷[11]。但是如果将同一个信号分别采用宽窗函数和窄窗函数作两次谱图分析，得到分别具有高频率分辨率和高时间分辨率的两组结果，再将两种结果综合（将两组时频矩阵进行Hadamard积运算[12]），就可以得到具有较好时频聚焦性的时频分析结果。

3.2 改进的组合式谱图法

具体算法如下：

（1）对于信号s(t)分别采用不同长度的窗函数hl(t)、hs(t)进行时频变换，得到SPECl(t，ω)和SPECl(t，ω)。

（2）根据门限ε对SPECl(t，ω)和SPECs(t，ω)进行截断处理。

其中，ε=η×mean(SPEC(t，ω))。信噪比较低时，可降低η值，利于保留跳频信号；信噪比较高时，可提高η值，提高算法的分辨率。

（3）将得到的两组结果SPEC′l和SPEC′s进行Hadamard积，即可得到组合谱图分析结果。

3.3 算法性能比较

3.3.1 仿真比较

根据公式（1）在计算机中生成一段跳频信号，跳频周期为0.05 s。

图1～图4分别为短时傅里叶变换、谱图法、维格纳-维尔分布和组合谱图法的时频分析结果。对比四种算法，可以看出：谱图的效果稍好于短时傅里叶变换；维格纳-维尔分布具有最高的时频分辨率，但是存在大量的交叉项；组合谱图法的分辨率较原算法有非常大的提升。

3.3.2 信息熵比较

在对比不同时频分析方法的性能时，仅靠肉眼观察不能准确地反应算法性能的好坏。文献[13]提出用信息熵作为指标来评价双线性时频分布的性能，在该方法中，信息熵由时频分辨率和交叉项共同决定，只能给出总体评价，不能单独体现分辨率和交叉项的性能指标，但当一种性能指标相同的情况下，可以反映出另一性能的相对关系。例如，应用在线性分析方法中时，由于不存在交叉项，因此信息熵可以作为算法的频分辨率的量化指标。信息熵的数学表达式为：

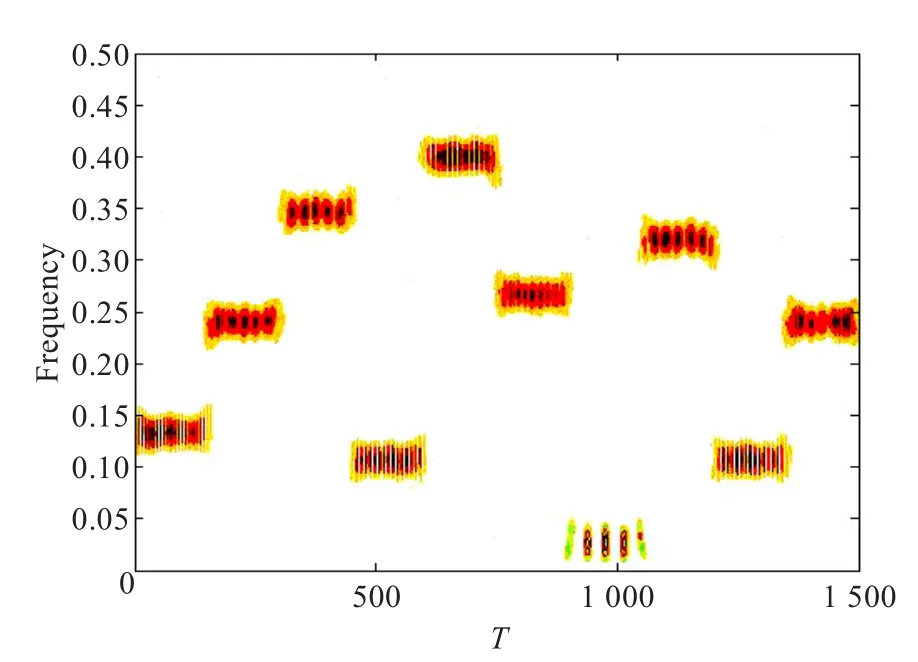
图1 短时傅里叶变换

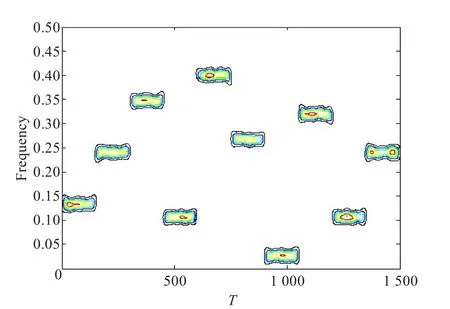
图2 谱图法

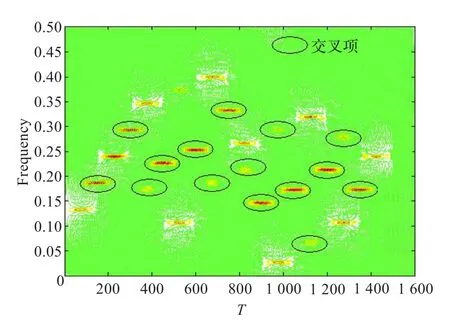
图3 维格纳-维尔分布

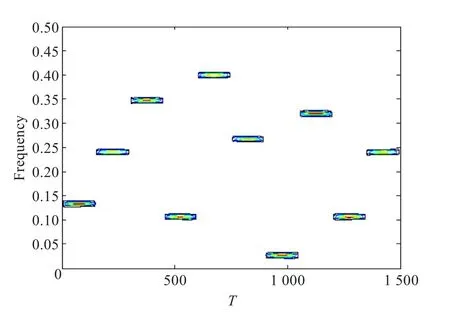
图4 组合谱图法

计算方法如下：

（1）计算出信号的时频分布幅值。

（2）搜索时频幅值的区间[TFmax(t，ω)，TFmin(t，ω)]，将该区间平均分成N组子区间，每个子区间宽度为[TFmax(t，ω)-TFmin(t，ω)]/N，对时频幅值进行统计，得到N组幅值区间的概率P(p1，p2，…，pN)。

（3）计算时频表示的信息熵。

对于同一个信号，时频分布的信息熵值越小，代表时频分辨率越好。四种算法的信息熵值如表1所示。

表1 四种算法的信息熵值比较

谱图法的信息熵小于短时傅里叶变换，而维格纳-维尔分布由于存在交叉项干扰，因此信息熵不能准确地反应其分辨率，组合谱图法信息熵较原算法提高了2.8倍。

3.3.3 e指数轮廓比较

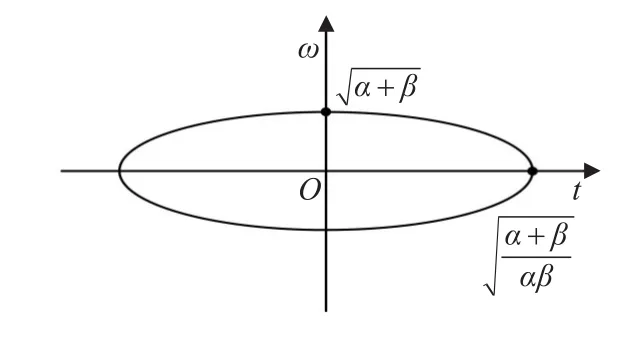
图5 谱图法中e指数轮廓

根据式和组合谱图法的定义，组合谱图法的表达式可以写成：

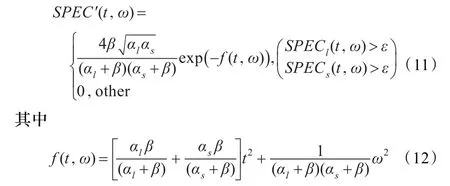
由于进行了截断处理，因此组合谱图法中e指数轮廓为两个椭圆轮廓的重叠部分，如图6所示。

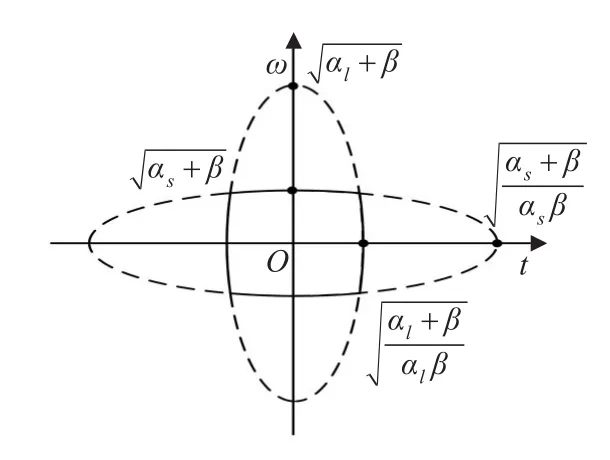
图6 组合谱图法中e指数轮廓（实线部分）

3.4 参数估计性能

在得到跳频信号的时频分析结果后，可对跳频信号的参数进行估计。例如沿时间轴搜索每个时刻对应的最大值，可得到一个具有周期性的信号波形，该信号的周期即为跳频信号的跳频周期，其倒数为跳速[12]。

在高斯白噪声条件下，采用组合谱图法对跳频信号的跳速进行了估计。若估计结果与实际值间的相对误差小于1%，则认为本次估计正确。本文在不同的信噪比情况下，进行了1 000次仿真，结果如图7所示，组合谱图法的信噪比性能提升了3 dB左右。

4 总结和下一步工作

提出了一种改进的组合谱图分析算法，通过理论分析和实验仿真，证明了本文算法在继承谱图法在分析跳频信号优点的同时，具有更高的时频分辨率，同时应用于参数估计中时具有更好的性能。但是该算法也存在复杂度增加，且窗口长度不能自适应信号频率变化等缺点，在下一步工作中将继续改进这些不足。

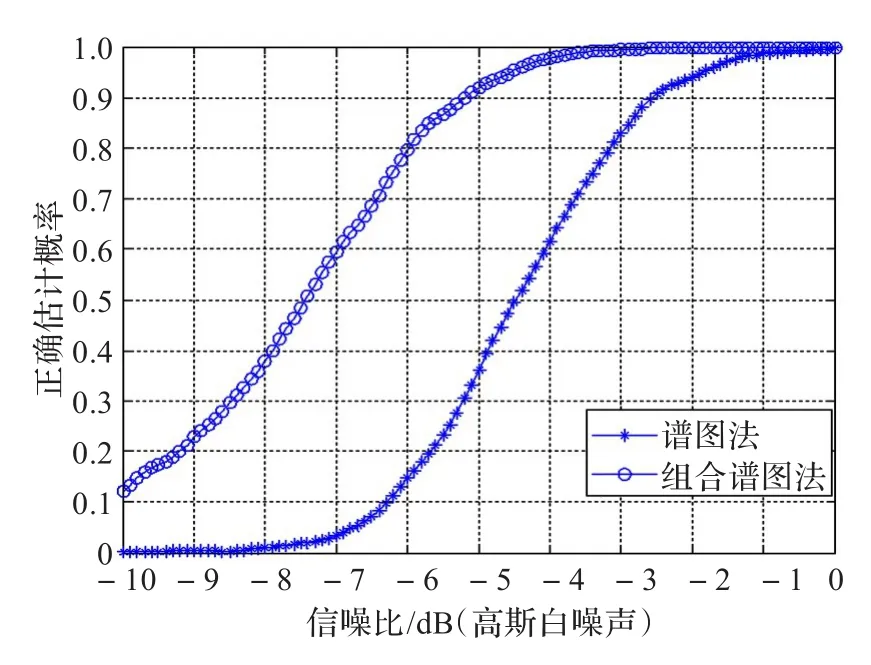
图7 跳频信号的跳速估计性能曲线

[1]郭建涛.随机跳频信号的模糊函数与时频分析[J].计算机工程与应用，2008，44（18）：121-123.

[2]Potter R K，Kopp G A，Green H C.Visible speech[M].New York，NY：Van Nostrand，1947.

[3]Ville J.Theorie et application de la notion de signal an-alytique[J].Cables et Transmissions，1948，2A：61-74.

[4]Zhang Y，Mu W，Amin M G.Subspace analysis of spatial timefrequency distribution matrices[J].IEEE Trans on SP，2001，49（4）：747-758.

[5]Roshan-Ghias A，Shamsollahi M B，Mobed M，et al.Estimation of modal parameters using bilinear joint time-frequency distributions[J].MechanicalSystemsandSignalProcessing，2001，21：2125-2136.

[6]邹红星，周小波，李衍达.时频分析：回溯与前瞻[J].电子学报，2000，28（9）.

[7]冯涛，袁超伟.一种组合时频分布在跳频信号参数估计中的应用[J].西安电子科技大学学报：自然科学版，2010，37（6）.

[8]Morlet J.Wave propagation and sampling theory-part：sampling theory and complex waves[J].Geophysics，1982，47（2）：222-236.

[9]Hippenstiel R，Khalil N，Fargues M.The use of wavelet-based detection of frequency hopping signals[J].Systems and Computers，1997（1）.

[10]秦前清，杨宗凯.实用小波分析[M].西安：西安电子科技大学出版社，1994.

[11]平殿发，赵培洪，邓兵.分数阶Fourier变换在多分量信号谱图分析中的应用[J].计算机工程与应用，2010，46（32）：116-118.

[12]陈利虎.跳频信号的侦察技术研究[D].长沙：国防科学技术大学研究生院，2009.

[13]熊良才，史铁林，杨叔子.Choi-Williams分布参数优化及其应用[J].华中科技大学学报：自然科学版，2003，31（1）：103-104．

[14]唐向宏，李齐良.时频分析与小波变换[M].北京：科学出版社，2008.

ZENG Xiangfeng1,YANG Yuhong1,CUI Penghui1,WEN Zhou2

1.Institute of Information Engineering,Information Engineering University,Zhengzhou 450002,China
2.Unit 65021 of PLA,China

A new combined spectrogram method is proposed for Frequency-Hopping（FH）signal analysis,which adopts two windows with different length to analyze the signals and gets two kind of results separately with better time-resolution and better frequency-resolution.By combined the advantage of two kinds of results,the time-frequency resolution is improved,and the improvement is proved by theoretical analysis and simulation results.At last,the performance in hop rate estimating with Gauss white noise has been given by simulation,the results show that the SNR（Signal Noise Ratio）performance enhances about 3 dB.

Frequency-Hopping（FH）signal;time-frequency analysis;combined spectrogram;parameter estimation

提出了一种应用于跳频信号的组合式谱图时频分析方法，采用两种不同长度的窗函数对信号进行时频分析，分别得到具有较好频率和时间分辨率的两组分析结果；结合两组结果的优点，提高了原谱图法的时频分辨率，并通过理论分析和仿真结果予以证明。在高斯白噪声条件下，对组合谱图法在跳速估计中的性能进行仿真，结果表明该算法的信噪比性能较谱图法提高了3 dB左右。

跳频信号；时频分析；组合谱图法；参数估计

A

TN911

10.3778/j.issn.1002-8331.1110-0679

ZENG Xiangfeng,YANG Yuhong,CUI Penghui,et al.Applications of combined spectrogram to frequency-hopping signal analysis.Computer Engineering and Applications,2013,49（13）：89-92.

曾祥峰（1986—），男，硕士研究生，主要研究方向：卫星通信；杨育红（1964—），女，副教授，硕士生导师；崔鹏辉（1988—），男，硕士研究生；温洲（1983—），男，助理工程师。E-mail：geoffreyzeng@gmail.com

2011-11-07

2012-01-02

1002-8331（2013）13-0089-04

CNKI出版日期：2012-03-21http://www.cnki.net/kcms/detail/11.2127.TP.20120321.1738.057.html