基于EPFF算法的下料问题模型
徐标,陈昊,安佰玲
淮北师范大学 数学科学学院,安徽 淮北 235000
基于EPFF算法的下料问题模型
徐标,陈昊,安佰玲
淮北师范大学 数学科学学院,安徽 淮北 235000
1 问题重述
原料下料问题是企业生产中最为重要的问题之一。原材料利用率的高低直接反映着企业的生产水平,也是影响企业经济效益的主要因素之一,同时切割模式的单一化也有利于降低成本,提高生产率。因而提高原料利用率,减少切割方式对我国经济发展具有特别重要的意义。
“下料问题”是把相同形状的一些原材料分割加工成若干个不同规格大小的零件的问题,此类问题在工程技术和工业生产中有着重要和广泛的应用。
对单一原材料下料问题[1]进行探讨;设此种原材料是长度为L,宽度为W的长方形,现有这种长方形原料一批,要将其制作成m种型号的零件,全部零件均保持与原材料一样的厚度,但长度和宽度有所变化,分别为(l1,w1),(l2,w2),…,(lm,wm),其中wi<li<L,wi<W,i=1,2,…,m。m种零件的加工量分别为n1,n2,…,nm。加工时,零件的各边要分别和原材料的边相平行;这就是工程上所谓的二维下料问题。尤其当所有型号零件的宽度均与原材料相同,即wi=W,i=1,2,…,m,就是一维下料问题。
对于上述一维单一原材料下料问题,建立相应的数学模型,并同时求解下列问题:在生产能力允许的情况下给出满足要求的下料方案,然后求出完成相同任务所需的原材料数,并计算废料总长度和使用的下料方式数和。单一原材料的长度为3 000 mm,现有53种不同长度的零件需要加工。具体参数见文献[1]中表1,其中li为需求零件的长度,ni为需求零件的数量。此外,在每个下料点处,由锯缝所产生的损耗为5 mm。据估计,该企业每天下料的最大能力是100块,要求在4天内完成的零件标号(i)为:5,7,9,12,15,18,20,25,28,36,48;要求不迟于6天完成的零件标号(i)为:4,11,24,29,32,38,40,46,50。
2 问题分析与建模
2.1 问题分析
原材料利用率的高低直接反映着企业的生产水平,也是影响企业经济效益的主要因素之一。因而采用有效的方法,提高原材料的切割利用率,节约原料,对我国经济发展具有特别重要的意义。
下料问题可以归结为一个整数线性规划问题,可以使用分枝定界法、单纯形方法或者遗传算法进行求解,由于在要求下料的零件种数较多时,其线性规划的约束条件中的式子也较多,考虑使用Lingo软件进行求解。对于下料的方式采用EPFF算法求出所有的下料组合,代入模型中,求出最优解,同时确定所用的下料方式。
2.2 符号说明
L:原材料的长度(为3 000 mm);
W:原材料的宽度(为100 mm);
li:第i种零件的长度,i=1,2,…,p;
wi:第i种零件的宽度,i=1,2,…,p;
ni:第i种零件的需求量,i=1,2,…,p;
(xkj):下料方案矩阵,即第k天以第j种下料方式切割的原材料块数,j=1,2,…,q ,k=1,2,…,d;
(aij):下料方式矩阵,即第j种下料方式下每块原材料生产第i种零件的数量,i=1,2,…,p,j=1,2,…,q;
(si):第i类零件在某种下料方式下切割数量;
ci:第i类零件的面积,即ci=liwi;
c:每天的最大生产能力;
z:所需要的原材料数;
v:材料利用率(%);
m:采用的下料方式个数。
2.3 建立模型
建立一个以消耗原材料总数最小为目标,下料方式又少的整数线性规划[2-3]数学模型,目标函数为:
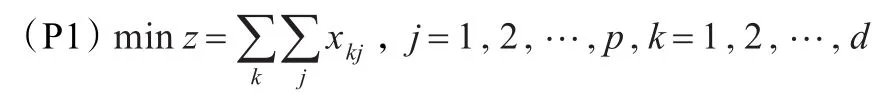
要求满足一定的生产能力,即每天的生产总量不大于c,则有约束条件:

同时要求满足需求量,有约束条件:
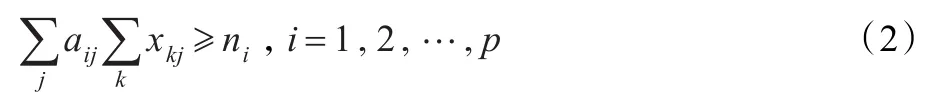
对于有时间限制的模型,则要给出给定时间内生产数量的下界约束,即:

i为要求在给定时间内完成的零件标号,xkj≥0,aij≥0且为整数。
至此,一维单一原材料实用下料问题的数学模型建立起来了,其中的第j种下料方式下每个原材料生产第i种零件的数量aij在零件种类比较少的情况下,可以采用枚举法确定下料方式。对于零件种类比较多的,采用Lingo求解没有可行解,无法给出下料方式矩阵。因此采用EPFF算法,用Matlab编程求出相应的下料方式,代入模型中,再交给Lingo求解,就求出了可行解,结果中可以确定具体采用了哪种下料方式使结果达到最优。原材料的平均利用
3 模型的求解
现有单一原材料的长度为3 000 mm,需要完成一项有53种不同长度零件的下料任务。此外,在每个下料点处由锯缝所产生的损耗为5 mm。企业每天最大下料能力是100块,又要求分别在4天、6天内完成不同类型的零件,给出最优方案。
首先确定下料方式矩阵(aij)p×q,同时将锯缝所产生的损耗为5 mm考虑在内。由于零件种类有53种,使用枚举法工作量太大,不可行,采用Lingo求解没有可行解,也无法解出下料方式矩阵。这里采用EPFF算法,应用Matlab编程求解,给出下料方式矩阵。
一维下料问题可建模为装箱问题。冯晓慧[4]等的EPFF算法是求解装箱问题的一种较新的算法,它将所有的箱子分成8组,将实数列中的元素分成8类,称(2/3,1),(7/12,2/3),(1/2,7/12),(5/12,1/2),(1/3,5/12),(1/4,1/3),(1/5,1/4),(0,1/5)上的元素分别为α1,α2,α3,β1,β2,β3,β4,γ共8类元素,同时用a1,a2,a3,b1,b2,b3,b4,r分别表示8类元素的数目。EPFF算法步骤如下:
(1)从β2,β3,β4类元素中取出a3个元素与α3类元素放在一起(若a3>(b2+b3+b4),则取完所有的β2,β3,β4类元素为止),再从β3,β4类元素中取出a2个元素与α2类元素放在一起。
(2)将α1类元素装入第1组箱子中,每个箱子中装入1个元素。
(3)将α2类元素及取出的β3,β4类元素装入第2组箱子中,每个箱子最多装1个α2类元素和1个β3或β4类元素。
(4)将α3类元素及取出的β2,β3,β4类元素装入第3组箱子中,每个箱子最多装1个α3类元素和1个β2或β3或β4类元素。
(5)将β1类元素及余下的β2,β3,β4类元素分别装入第4~7组箱子中,各组箱子分别装2,2,3,4个β1,β2,β3,β4类元素。
(6)将γ类元素按FF算法[4]装人第8组箱子中。
这样,利用Matlab编程最终就得到下料方式矩阵(aij)p×q,为53×62的矩阵。
首先考虑了4天的下料方式,建立模型如下:
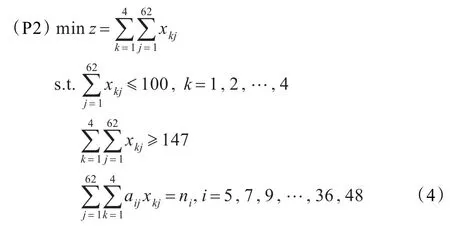
同样,可以得到6天的下料方式,其模型与4天的相似。但是,这些只是从局部考虑问题,二者得到的解不能统一到整体之中。于是,综合二者于一个模型之中,制定出有4天、6天限制的53种零件的下料方案。在Matlab中用EPFF算法的计算结果得到需要的总原料数量约为809块,这样,估计需要d=9天,可以顺利完成任务。于是得到模型:

表1 每天下料方式及相应切割的原材料块数

用Lingo[8]编程求解得到可行解z=808块,以及每天使用的下料方式和在该种方式下切割的原材料块数,如表1所示。
从表1中可以看出,第2天使用的下料方式有12、17、19、53、54,它们切割的原材料块数分别为8块、32块、32块、1块、27块。其他依此类推。
由此可以计算出材料利用率:
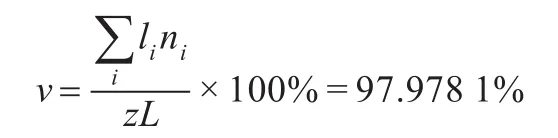
使用的下料方式有m=51种,废料总长度为49 011 mm。
4 结束语
若单纯采用线性整数规划建立数学模型,则由于零件种类以及下料方式过多而无法得到最优解,给不出下料方式阵;若仅采用EPFF算法,通过编写程序建模,则由于无法考虑对某些零件的加工时间的限制而使得到的解只是一个等额加工完所有零件的整体方案,无法给出具体每一天的加工方案。因此,综合考虑两种方式,建立了混合型模型,很好地解决了实用下料问题,得到了较少的下料方式和较高的原材料利用率。本模型具有思路简洁,易于操作,适用性强等特点。
[1]第一届全国研究生数学建模竞赛试题[EB/OL].[2012-08-10]. http://gmcm.seu.edu.cn/s/274/t/1419/68/70/info26736.htm.
[2]运筹学教材编写组.运筹学[M].3版.北京:清华大学出版社,2005.
[3]胡祥培.运筹学讲义.大连:大连理工大学管理学院,2001.
[4]冯晓慧,李菊娥,任春丽.装箱问题的一种新算法及其性能比的证明[J].西安电子科技大学学报,1998,25(2):231-233.
[5]姜启源.数学模型[M].北京:高等教育出版社,2003.
[6]萧树铁,姜启源,何青,等.数学实验[M].北京:高等教育出版社,1999.
[7]李琼,金升平.一维优化下料问题的模型与算法的综合比较[J].武汉交通科技大学学报,1998,22(4).
[8]谢金星,薛毅.优化建模与LINDO/LINGO软件[M].北京:清华大学出版社,2006.
[9]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.
[10]刘润涛,陈媛婧.型材下料问题算法研究[J].计算机工程与应用,2009,45(25):215-217.
[11]包奇金宝,姜静清,宋初一,等.基于粒子群与模拟退火算法的板材优化下料[J].计算机工程与应用,2008,44(26):246-248.
XU Biao,CHEN Hao,AN Bailing
School of Mathematical Science,Huaibei Normal University,Huaibei,Anhui 235000,China
The cutting-stork-problem of a single one-dimensional materials is considered,with optimal and EPFF algorithms, the hybrid model is built.Namely the cutting way array is obtained with EPFF algorithm,then it is substituted into the linear programming model.Under the limitation of the processing time and the maximum processing capacity,it gets the requirements of practical cutting program.
integer programming;cutting-stork-problem;EPFF algorithms;material utilization
研究一维单一原料下料问题,将最优化模型和EPFF算法相结合,建立了混合型模型,即先采用EPFF算法得到下料方式阵,再将其代入线性规划模型中,加上了加工时间以及最大加工能力的限制;最后确定了满足要求的实用下料方案。
整数规划;下料问题;EPFF算法;材料利用率
A
O29
10.3778/j.issn.1002-8331.1303-0090
XU Biao,CHEN Hao,AN Bailing.Models of cutting stork problem based on EPFF algorithms.Computer Engineering and Applications,2013,49(13):56-58.
国家自然科学基金(No.11171156);安徽省高等学校省级自然科学研究项目(No.KJ2012Z346,No.KJ2013Z285);皖淮北师范大学青年科研项目(No.700437)。
徐标(1981—),男,讲师,研究方向为数值计算方法,数理统计与建模;陈昊(1982—),男,讲师,研究方向为偏微分方程数值解;安佰玲(1977—),女,讲师,研究方向为金融数学与建模。E-mail:xubiao512@163.com
2013-03-08
2013-04-30
1002-8331(2013)13-0056-03
◎网络、通信、安全◎

