气象遥感图像及格点场重采样插值方法
叶金印,邱旭敏,黄 勇,张春莉
1.淮河流域气象中心,安徽 蚌埠 233040
2.安徽省气象科学研究所,合肥 230031
气象遥感图像及格点场重采样插值方法
叶金印1,邱旭敏1,黄 勇2,张春莉1
1.淮河流域气象中心,安徽 蚌埠 233040
2.安徽省气象科学研究所,合肥 230031
1 引言
气象遥感图像产品和气象格点场资料在天气预报业务和科研中发挥着不可替代的作用[1-2],尤其是在气象客观自动化预报中备受关注[3-4]。气象业务数据按表现形式分为两类:一类是非规则的离散类数据,如气象站点观测数据;一类是规则的格点(栅格)类数据,如气象遥感图像及数值天气预报格点场。在气象业务尤其是科研中,常常需要对各类资料进行融合,以便于气象成因分析。原始气象遥感图像和气象格点场的分辨率和地图投影方式往往不同[5],若要对它们进行综合分析,需要进行重采样插值处理。对规则的格点(栅格)类数据进行重采样插值是首要环节,也是重要的环节之一。气象遥感图像产品都是以某种地图投影方式表现的,与在经纬网格坐标系中表现的气象格点场无法直接匹配,需要将气象遥感图像重采样插值到经纬网格坐标系。同时,以经纬网格坐标系表示的数值天气预报产品(如降水预报格点场),也因数值预报模式不同而具有不同的分辨率和区域范围[6-7];除数值天气预报格点场外,其他气象格点(栅格)场也存在使用不同分辨率表示的问题[4];为便于预报自动化和科学研究,也需要将不同分辨率的气象格点场插值到相同分辨率的经纬网格坐标系中。
从不同研究目的和应用需求出发,对于图像重采样和插值方法研究有不同的侧重,如王茂新等人针对气象卫星NOAA/AVHRR数据的特点,提出了三次卷积法、双线性内插法等几种常规采样算法[5]。楼绣林等人又针对重采样速度慢的问题提出了一种重采样的快速算法,利用“块操作”快速确定重采样图像中任意像元点在原始图像中的位置,同时提出了邻点权重法代替其他插值方法[8]。一般图像处理中的重采样插值主要用于对图像本身的放大(缩小)和几何校正;对于气象业务中使用的气象遥感图像,重采样插值主要通过地图投影坐标转换来提取以及填补气象信息。邻点权重法是图像产品插值方法中最为实用的一种[8],而最近邻点法[9]是在计算方法上与邻点权重法最为接近的一种。因此,本文对不同分辨率的气象遥感图像产品,分别采用邻点权重法及最近邻点法进行重采样插值,并对插值结果进行分析。
双线性插值方法在图像和格点场插值中的应用比较广泛,且效果较好[10]。李得勤等人采用双线性插值方法对数值预报模式产品进行降尺度处理,发现插值结果与实际观测的均方根误差以及相关系数和插值前相差甚小[11]。王岳山首次将贝塞尔插值方法应用在数值预报格点场插值中,指出采用贝塞尔方法进行插值不仅速度快而且精度也非常高[12]。因此,本文对不同分辨率的气象格点场资料分别采用贝塞尔插值及双线性插值方法插值,并对插值结果进行分析。
2 气象遥感图像重采样插值方法
气象遥感图像重采样插值的目的是将一个坐标系中的点阵信息在另一个坐标系中按一定格式“最逼真地”表示出来。基本方法有直接法和间接法,如图1所示。直接法,是从某一种地图投影坐标的原始图像上的像元点坐标出发,按照地图投影坐标转换公式求出目标坐标系中像元点对应的坐标,然后将原始图像上像元点(x,y)处的数据直接赋予或经过插值赋予目标坐标系(X,Y)处的像元点。间接法,是从目标坐标系的像元点坐标出发,按照地图投影坐标转换公式求出原始坐标系中像元点的坐标,然后将原始坐标系中像元点(x,y)处的数据直接赋予或经过插值赋予目标坐标系中(X,Y)处的像元点。

图1 直接法和间接法示意图
气象遥感图像重采样插值关键环节有2个:地图投影坐标向目标坐标系的转换以及对像元点数据进行插值。本文以兰勃托投影卫星云图[13]为例,描述将其重采样插值到经纬网格坐标系中的方法。
2.1 地图投影坐标转换方法
地图投影坐标转换[14-15]有两种方式:(1)由目标坐标系(经纬网格坐标系)坐标值求出地图投影坐标系(兰勃托投影)中坐标值,称之为正解,即由经纬度计算投影坐标:(φ,λ)→(X,Y)。

(2)从地图投影坐标(兰勃托投影)向目标坐标系(经纬网格坐标系)转换,称之为反解。即由投影坐标计算经纬度:(X,Y)→(φ,λ)。

2.2 像元点数据插值方法
(1)最近邻点法[9]:这种方法以距离被计算点最近的一个像元的灰度值作为输出像元的灰度值。仅通过距离比较,就近取值,仅有一个像元参与计算,因而计算效率高,但重采样插值效果较差,灰度的连续性受到一定程度的破坏。
(2)邻点权重法,其示意图如图2所示。

图2 邻点权重法示意图
插值点p周围4个原始像元点的灰度值都参与计算,根据距离d的不同,各个像元点灰度值的贡献不同,距离小的像元贡献大,距离大的像元贡献小。由于“邻点权重法”在决定插值点灰度值时距离起决定作用,能够尽可能多地保持原图像的信息。
两种插值方法相比,邻点权重法的计算量显然要大于最近邻点法的计算量。
2.3 气象遥感图像重采样插值方法的实现
直接法和间接法不同之处在于投影变换中源坐标系和目标坐标系的选择不同。坐标转换后,对像元点的插值方法可以根据需要选取合适的方法,如最近邻点法及邻点权重法。
直接法实现步骤:首先建立一个经纬网格坐标系,利用地图投影坐标转换反解公式解析出原始图像每个像元点的经纬度(φ,λ),进而对经纬度坐标系上每一个网格点(φi,λi)进行插值。在插值方法上,最近邻点法需要对原始图像中所有像元点的经纬度进行判断,来找出距离所求网格点(φi,λi)最近的像元点,将像元点的灰度值赋予该点;邻点权重法则需要找出距离该点最近的周围4个像元点,判断过程复杂,计算量大。
间接法实现步骤:首先建立一个经纬网格坐标系,再从该经纬网格坐标系出发,利用地图投影坐标转换正解公式计算出每个网格点(φi,λi)在原始图像中的坐标点(X,Y),计算出坐标点(X,Y)周围的4个像元点坐标,即原始图像横轴方向第i和第i+1及纵轴方向第j和第j+1的4个交叉点。进而对该坐标点(X,Y)进行插值,并将值赋予网格点(φi,λi)。在插值方法上,最近邻点法仅需找到距离坐标点(X,Y)最近的像元点,并将值赋予网格点(φi,λi)。邻点权重法需要找到距离坐标点(X,Y)周围的4个像元点,并按照距离权重对灰度值进行插值计算。
比较直接法和间接法的计算过程,间接法重采样插值的计算量远小于直接法。
3 气象格点场插值方法
与气象站观测数据(不规则离散数据)不同的是,数值天气预报模式输出的客观分析场和要素预报场均以一定经纬网格距的格点场表示,不同数值天气预报模式输出产品具有不同的经纬范围和分辨率。针对业务和科研的需要,常常要把不同分辨率的数值预报模式输出产品进行标准化,形成一定经纬度范围内分辨率相同的气象格点场。本文以数值天气预报模式输出的规则格点场为例,比较分析双线性插值方法和贝塞尔插值方法的插值效果。
3.1 双线性插值方法
双线性插值,又称为双线性内插。在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值。假如想得到未知函数f在点P=(x,y)的值,假设已知函数f在Q11=(x1,y1)、Q12=(x1,y2)、Q21=(x2,y1)以及Q22=(x2,y2)四个点的值。首先在x方向进行线性插值,得到R1和R2,然后在y方向进行线性插值,得到P。双线性插值示意图如图3所示。
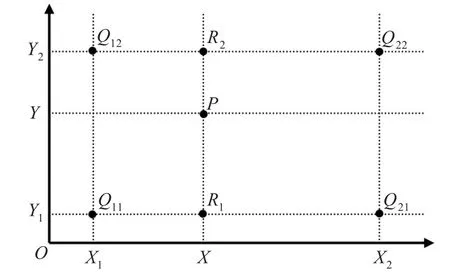
图3 双线性插值示意图
3.2 贝塞尔插值方法
将贝塞尔公式[12]以中央差分格式写成插值公式,只保留到第二阶差分:

其中,t=(x-x0)/h,h是格距。
y-1、y0、y1、y2分别为同一条直线上相邻的4个点x-1、x0、x1、x2的值,y为位于x0与x1之间的点x的值。将贝塞尔插值方法应用到气象格点场插值中,需要在两个方向上分别进行一次插值:先在x方向上进行贝塞尔插值,再在y方向上进行贝塞尔插值,得到最终结果。
4 应用分析
4.1 气象遥感图像重采样应用分析
本文从气象业务科研需求出发,对直接法和间接法重采样插值的效果进行分析,重点分析评估易于实现的间接法中最近邻点法和邻点权重法的插值效果。
以气象业务中应用的FY2E和FY2D兰勃托投影红外卫星云图为例,进行重采样插值应用分析。FY2E红外云图像元点阵为512×512,像素点间距为13.0 km,投影中心点经纬度为:(110°E,30°N),左下角经纬度为:(86.59°E,0.64°S);FY2D红外云图像元点阵为1 200×1 200,像素点间距为4.9 km,投影中心点经纬度为:(100°E,35°N),左下角经纬度为:(77.32°E,6.59°N)。
(1)直接法重采样插值应用分析:图4(a)及图4(b)分别为FY2E兰勃托投影红外云图(2011年12月7日8时,GMT+ 8)原始图像和采用直接法进行地图投影坐标转换后的图像(Fortran SGL绘图,窗口分辨率为1 200×700,下同)。FY2E红外云图经过直接法地图投影坐标转换后共有512× 512个像元点。由图4可以看出,在高分辨率目标坐标系中,低分辨率的FY2E红外云图经过地图投影转换后,像元点之间有很明显的间隙(灰度值为空)。

图4 (a)FY2E红外云图

图4 (b)经过直接法投影转换后的图像
图5(a)及图5(b)分别为FY2D(2012年8月9日8时15分,GMT+8)兰勃托投影红外云图原始图像和采用直接法进行地图投影坐标转换后的图像(Fortran SGL绘图)。FY2D红外云图经过直接法地图投影坐标转换后共有1 200×1 200个像元点。由图5可以看出,目标坐标系分辨率与原始图像分辨率基本一致的情况下,高分辨率的FY2D红外云图经过地图投影坐标转换后的图像并没有显现出间隙。
比较图4(b)与图5(b)发现,对于高分辨率目标坐标系而言,低分辨率的图像相对于高分辨率的图像,采用直接法重采样时存在更多的需要插值的“间隙”。低分辨率图像因坐标转换后的像元点间隙明显,最近邻点法的插值会有较大误差;而邻点权重法可以在一定程度上减小这种误差。高分辨率图像因坐标转换后的像元点间隙不明显,最近邻点法的插值误差与邻点权重法的误差比较接近。由此可见,随着图像分辨率的提高,最近邻点法在重采样插值效果上会更接近于邻点权重法,且因为计算简单,在计算量上会小于邻点权重法。

图5 (a)FY2D红外云图

图5 (b)经过直接法投影转换后的图像
(2)间接法重采样插值应用分析:根据FY2E和FY2D红外云图分辨率及投影位置分别建立与之对应的重采样经纬网格坐标系:FY2E重采样区域选为10°N~50°N,90°E~130°E,网格间距0.1°;FY2D重采样区域选为10°N~50°N,80°E~120°E,网格间距0.05°。分别采用最近邻点法及邻点权重法对其进行重采样插值。
图6为FY2E红外云图最近邻点插值与邻点权重插值结果在Fortran SGL中的显示。其中,图6(c)和图6(d)分别为图6(a)和图6(b)局部特征放大图像。比较图6(c)和图6(d)可以看出,低分辨率的FY2E红外云图采用两种插值方法得到的图像在纹理和清晰度上存在明显差异。

图6 FY2E红外云图插值结果在Fortran SGL中的显示
图7为FY2D红外云图最近邻点插值与邻点权重插值结果在Fortran SGL中的显示。其中,图7(c)和图7(d)分别为图6(a)和图6(b)局部特征放大图像。比较图7(c)和图7(d)可以看出,高分辨率的FY2E红外云图采用两种插值方法得到的图像在纹理和清晰度上未表现出差异。
图8为FY2E和FY2D红外云图的最近邻点法插值与邻点权重法插值结果在MICAPS(气象信息综合分析处理系统)[16]中的叠加显示。其中,图8(c)和图8(d)分别为图8(a)和图8(b)局部特征放大图像。可以看出:低分辨率的FY2E红外云图的最近邻点插值与邻点权重插值结果等值线有明显不吻合,邻点权重法插值结果与原始图像更为接近;而高分辨率的FY2E红外云图的最近邻点插值与邻点权重插值结果等值线几乎吻合,且与原始图像完全吻合。

图7 FY2D红外云图插值结果在Fortran SGL中的显示
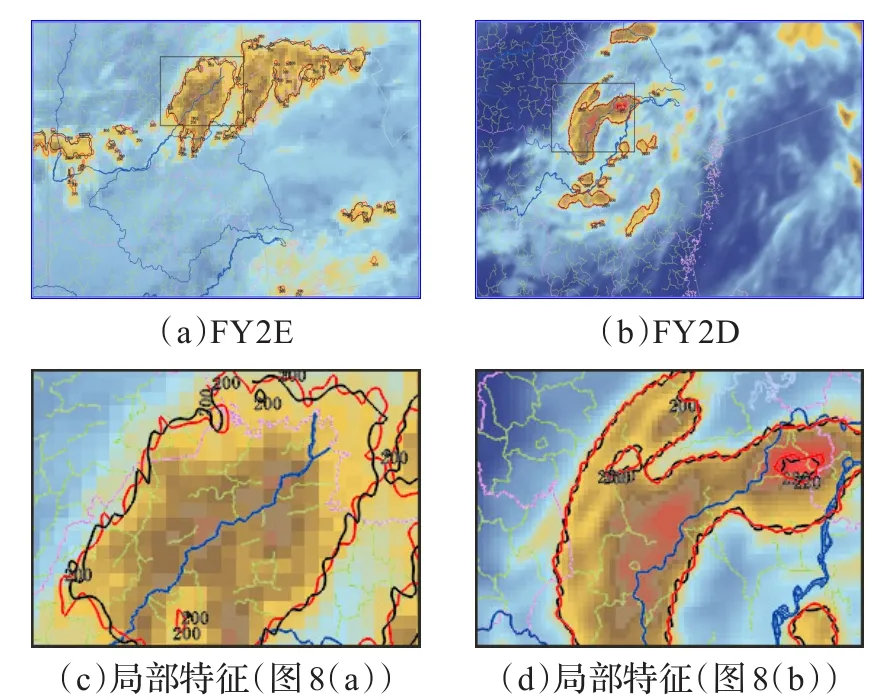
图8 最近邻点法(红线)与邻点权重法(黑线)插值结果在MICAPS中的叠加显示
为定量评估两种插值方法的效果,引入清晰度进行分析。清晰度[17]一般使用平均梯度衡量,公式为:

式(4)中F为平均梯度,G(x,y)为影像函数,m,n为影像的行列数。根据相对误差来分析方法之间效果的差异,公式为:

式(5)中f为相对误差,v1为比较图(数据)参数,v2为原始图(数据)参数。
表1为最近邻点法及邻点权重法清晰度统计分析结果。对不同分辨率的图像,最近邻点法相对于邻点权重法的清晰度相对误差分别为14.171%(FY2E)和1.849%(FY2D)。对于低分辨率图像(FY2E),最近邻点法在重采样插值效果上与邻点权重法有较大差距;而对于高分辨率图像(FY2D),两者差距不大。

表1 最近邻点法及邻点权重法清晰度
由此可见,随着图像分辨率的提高,最近邻点法在重采样插值效果上会更加接近邻点权重法,且最近邻点法计算方法简单、计算量小。在客观预报自动化业务中,对于高频次、高分辨率遥感图像,重采样插值采用最近邻点法更为实用。
4.2 气象格点场插值结果分析
以气象业务中日常应用的欧洲中期天气预报中心(ECMWF)降水预报场(2012年8月13日20时,GMT+8)为例进行插值方法分析。欧洲中期天气预报中心降水预报场是间距为0.25°的等经纬距格点场,区域范围为0°E~180°E、0°N~90°N。
分别采用贝塞尔插值和双线性插值将其插值为网格距为0.2°的等经纬距格点场,区域范围取在114°E~120°E、29°N~35°N。图9为两种插值结果与原降水预报场在MICAPS系统中叠加显示图。贝塞尔插值结果与原始降水场等值线基本吻合(图9(a)),而双线性插值结果与原始降水场等值线吻合度不如贝塞尔插值(图9(b))。

图9 ECMWF降水预报场(红线)与两种插值结果(黑线)叠加显示图
表2为降水预报原始场以及采用贝塞尔和双线性插值的统计分析结果,贝塞尔插值结果相对于降水原始场,标准差相对误差0.640%,平均值相对误差0.226%;而双线性插值标准差相对误差3.025%,平均值相对误差0.605%。可以看出贝塞尔插值结果与双线性插值结果均较为接近原始场,贝塞尔插值结果优于双线性插值。

表2 两种插值方法结果统计
为进一步分析两种插值方法的效果,对原始降水预报场等间距抽点,形成分辨率为0.5°的格点场,分别采用贝塞尔插值方法及双线性插值方法将其插值到与原始场分辨率相同的0.25°的格点场。以0.25°原始场为参照,对比分析采用不同插值方法所生成的0.25°格点场。图10为两种插值结果与原始降水预报场在MICAPS系统中叠加显示图。由图10(a)及图10(b)对比可以看出,贝塞尔插值与双线性插值效果差别比较明显,这种差别在降雨中心区域表现得更加明显。

图10 ECMWF降水预报场(红线)与两种插值结果(黑线)叠加显示图
表3为降水预报原始场以及经抽点后采用贝塞尔和双线性插值得到降水预报场的统计分析结果。贝塞尔插值结果相对于降水原始场,方差相对误差2.225%,平均值相对误差0.546%;而双线性插值方差相对误差4.242%,平均值相对误差0.664%。从统计结果看,可以同样得到贝塞尔插值方法的效果优于双线性插值方法。
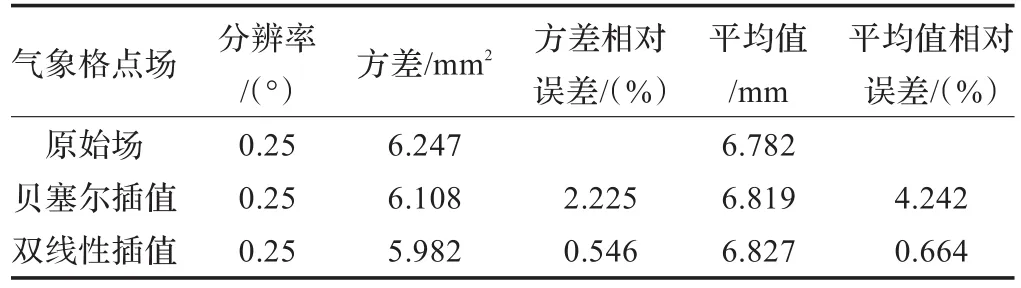
表3 两种插值方法结果统计(抽点试验)
5 结论
以气象业务中不同分辨率的气象卫星(FY2E和FY2D)遥感图像以及欧洲中期天气预报中心(ECMWF)降水预报场为例,分别对不同重采样插值方法进行了分析比较,得出如下结论:
(1)基于间接重采样的气象遥感图像最近邻点插值法的计算量小于邻点权重插值方法,而邻点权重插值方法的效果优于最近邻点插值方法。
(2)随遥感图像时空分辨率的提高,对于高频次、高分辨率的图像,采用基于间接重采样的最近邻点法在计算速度方面优势更加明显,在重采样插值效果上更加接近邻点权重法,能快速准确地完成图像重采样插值,更实用于客观自动化预报。
(3)对于数值天气预报模式输出的降水预报场,采用贝塞尔插值方法得到的插值结果更接近于原始场,贝塞尔插值方法的插值效果优于双线性插值方法。
(4)本文采用的气象遥感图像与气象格点场重采样插值方法具有很好的实用性,便于计算机实现和业务化。
[1]闵锦忠,沈桐立,陈海山,等.卫星云图资料反演的质量控制及变分同化数值试验[J].应用气象学报,2000,11(4):410-418.
[2]许小峰.中国新一代多普勒雷达网的建设与技术应用[J].中国工程学,2003,5(6):7-14.
[3]黎光清,董超华.卫星气象遥感和应用:现状、问题、前景[J].气象科技,1990,18(1):1-7.
[4]王玉斌,万玉发,罗兵,等.一种等值线填充并行算法[J].计算机工程与应用,2012,48(28):61-65.
[5]王茂新,沙奕卓,于莉.关于NOAA AVHRR图像重采样及投影方法的研究[J].中国图象图形学报,1997,2(1):38-42.
[6]杨学胜,胡江林,陈德辉,等.全球有限区数值预报模式动力框架的试验[J].科学通报,2008,53(20):2418-2423.
[7]梁利,林开平,黄海洪.几种数值预报模式在广西降水预报效果的比较[J].气象研究与应用,2012,33(2):1-4.
[8]楼绣林,黄韦艮,周长宝,等.遥感图像数据重采样的一种快速算法[J].遥感学报,2002,6(2):97-101.
[9]鲍文东,杨春德,邵周岳,等.几何精校正中三种重采样内插方法的定量比较[J].测绘通报,2009(3):71-72.
[10]管志杰,赵政.地图投影变换及其在GIS中的应用[J].计算机工程与应用,2000,36(6):50-52.
[11]李得勤,陈力强,周晓珊,等.风电场风速降尺度预报方法对比分析[J].气象与环境学报,2012,28(6):25-31.
[12]王岳山.贝塞尔插值及其在数值预报中的应用[J].海洋学报,1995,12(2):12-17.
[13]许建民,张文健,杨军,等.风云二号卫星业务产品与卫星数据格式实用手册[M].北京:气象出版社,2008.
[14]Coordinate conversions and transformations including formulas[EB/OL].[2012-12-26].http://www.docin.com/p-25267998. html.
[15]廖宇.一种基于NSCT分解的图像插值算法[J].计算机工程与应用,2012,48(8):176-178.
[16]李月安,曹莉,高嵩,等.MICAPS预报业务平台现状与发展[J].气象,2010,36(7):50-55.
[17]何力,孙涵,黄永璘,等.MODIS1B数据的重采样方法研究[J].遥感信息,2007(3):39-44.
YE Jinyin1,QIU Xumin1,HUANG Yong2,ZHANG Chunli1
1.Huaihe River Basin Meteorological Center,Bengbu,Anhui 233040,China
2.Anhui Institute of Meteorology,Hefei 230031,China
Resampling interpolation method is one of the problems in the field of meteorological information processing research. This paper introduces a direct and indirect resampling interpolation methods which are based on map projection coordinate conversion for the meteorological remote sensing images,and introduces bilinear interpolation method and Bessel interpolation method for the meteorological grid point field.Taking meteorological satellite(FY2E and FY2D)remote sensing images with different resolutions and ECMWF(European Centre for Medium-Range Weather Forecasts)precipitation forecast field for example,the paper analyzes different resampling interpolation methods.The results show that the calculation amount of the nearest neighbor algorithm is less than that of the weighted nearest neighbor algorithm based on indirect resampling method,while the weighted nearest neighbor algorithm can get better results than the nearest neighbor algorithm.With the improvement of resolution,the comparative advantage of calculation amount of the nearest neighbor algorithm is more obvious.The weighted nearest neighbor algorithm is more suitable for high-resolution meteorological remote sensing images.The results also show that Bessel interpolation algorithm is better than bilinear interpolation algorithm for the meteorological grid point field.
meteorological remote sensing images;meteorological grid point field;resampling;interpolation method
重采样插值方法是气象信息处理领域研究的问题之一。针对气象遥感图像,介绍了基于地图投影坐标转换的直接重采样插值方法和间接重采样插值方法;针对气象格点场,介绍了双线性插值方法和贝塞尔插值方法。以气象业务中不同分辨率的气象卫星(FY2E和FY2D)遥感图像以及欧洲中期天气预报中心(ECMWF)降水预报场为例,分别对不同重采样插值方法进行了分析比较。结果表明:基于间接重采样的气象遥感图像最近邻点插值法的计算量小于邻点权重插值方法,而邻点权重插值方法的效果优于最近邻点插值方法;随着图像的分辨率提高,最近邻点插值法与邻点权重插值方法相比,计算量小的优势更加明显;对于高分辨率的气象遥感图像建议采用基于间接重采样的最近邻点法;对于气象格点场,贝塞尔插值方法的插值效果优于双线性插值方法。
气象遥感图像;气象格点场;重采样;插值方法
A
TP311
10.3778/j.issn.1002-8331.1302-0211
YE Jinyin,QIU Xumin,HUANG Yong,et al.Resampling interpolation methods of meteorological remote sensing image and grid point field.Computer Engineering and Applications,2013,49(18):237-241.
国家自然科学基金(No.41275030,No.41105098);淮河流域气象开放研究基金(No.HRM201103)。
叶金印(1968—),男,高级工程师,主要从事水文气象学及数值分析的研究。E-mail:yejinyin@sina.com
2013-03-01
2013-05-21
1002-8331(2013)18-0237-05
CNKI出版日期:2013-06-08 http://www.cnki.net/kcms/detail/11.2127.TP.20130608.0953.005.html

