改进的P-M扩散方程在相干斑抑制中的应用

陈少波，侯建华，张 华

中南民族大学 电信学院，武汉 430074

改进的P-M扩散方程在相干斑抑制中的应用

陈少波，侯建华，张 华

中南民族大学 电信学院，武汉 430074

相干斑抑制是合成孔径雷达图像处理的一个非常重要的而又未完全解决的环节。目前主要有两种处理手段：多视处理和滤波后处理。多视处理是以降低图像的分辨率为代价的，因此人们更多地去研究滤波后处理技术。在过去的20年里，斑点噪声的后处理抑制算法得到了深入研究，涌现出许多较为成熟的算法。这些算法主要分两类：（1）基于局部统计特性的空域滤波[1-5]：Lee、Frost、Kuan和MAP，这类滤波算法大都基于均匀目标场景而提出来的；它们利用局部统计参数，能够有效地滤除斑点噪声。（2）基于多分辨率分析的算法，其典型思路为通过小波变换这种多尺度分解的方式将SAR图像变换到小波域，通过对小波域的系数进行重新调整来达到去斑的目的[6]。基于非线性扩散方程提出的滤波理论近年来在光学图像去噪方面取得了很好的应用。Yu Yongjian和Santiago Aja-Fernandez等人将各向异性扩散方程成功应用于相干斑抑制：SRAD[7]和DPAD[8]。这类算法的思路是：基于局域统计特性的自适应滤波器可以转化成线性扩散模型，于是他们将局部统计特性引入扩散系数中，得到了相应的去斑模型。SRAD方法与传统的空间滤波相比有更加好的相干斑抑制效果，但是也存在不足之处：该方法对目标的判断不准确，在迭代次数较多的情况下，会导致图像严重模糊。Yu Yongjian曾经在文献[7]中指出直接将加性噪声抑制的各向异性扩散方程用来抑制相干斑噪声时，不但不能抑制噪声，反而会增强相干斑；但可以先通过对图像取对数，将相干斑噪声转换为加性噪声，然后选取适合加性噪声抑制的各向异性扩散方程来对转化后的图像进行扩散处理；目前关于各向异性扩散方程对加性噪声的抑制算法的研究比较深入，因此思路将会更加宽广一点。

本文首先分析了对数变化对于相干斑噪声的影响，说明了适合去除加性噪声的P-M扩散方程应用到相干斑噪声抑制的可行性。其次，为了使P-M扩散方程在有效去除经过对数变换的相干斑噪声的同时保持SAR图像的边缘特征，对P-M扩散方程进行了分析改进：（1）在分析稳健统计学和各向异性扩散的联系的基础之上[9]，选择了性能稳定的扩散系数函数；（2）通过分析扩散方程的实际处理情况，对扩散过程中的关键参数梯度阈值进行了修改，使之更加符合实际的扩散过程，更加能保持图像的边缘特征[10]；（3）通过引进扩散停止判断准则，使处理过程既准确又高效。最后给出了本文所提出的相干斑噪声抑制算法具体的步骤，给出实验结果，并对实验结果进行了分析。

1 对数变换对相干斑噪声的影响

已知N视SAR图像的强度服从具有2N个自由度的Gamma分布[11]。

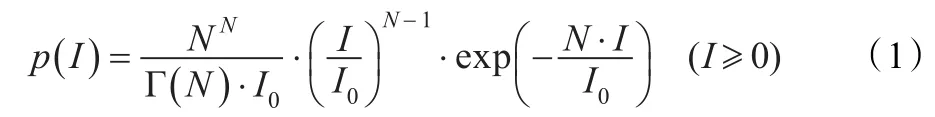
式中，I0为均值。Γ(N)为Gamma函数：

取对数变化，D=-ln(I)，则对数变换后相干斑噪声模型的概率密度为：

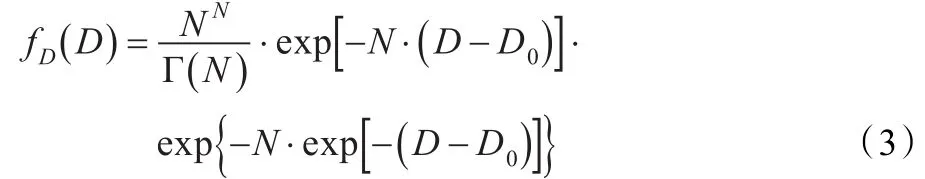
式中，D0=-ln(I0)，D0仅改变分布的位置而并不影响其形状。

为了简化表示，可设D0=0，则

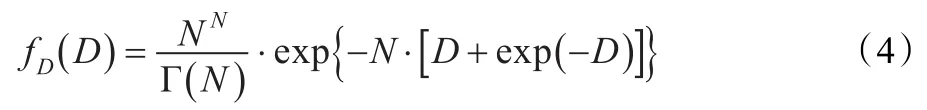
当N=1时，式（4）被称为Fisher-Tippett分布，而式（1）退化为指数分布。

对式（4）中的exp(·)项泰勒展开，取前三项，得到：

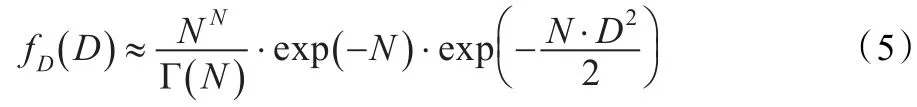
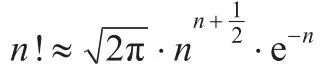
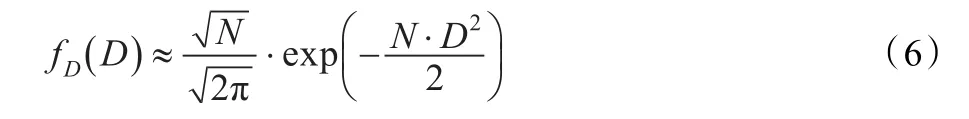
式（6）表明，在独立视数足够大时（通常N＞3就可得到较满意的近似），对数变化相干斑噪声近似为高斯白噪声，其方差是1/N。此时，式（1）也趋向高斯分布，但较式（6）慢很多。因此，把基于加性高斯噪声的图像滤波算法用于对数变化后的SAR图像比直接用SAR图像更加合适。

2 Perona-Malik模型分析

2.1 P-M扩散模型简介

P-M[12]模型在热传导方程的基础上加入了一个根据图像的位置控制扩散速度的函数C(x，y，t)，得到了以下的各向异性扩散模型：

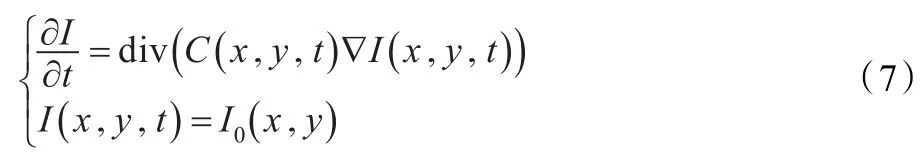
式（7）中：

最终，P-M模型的完整表达式为：

同时，Perona和Malik给出了g(s)的两种形式：

2.2 扩散系数特性分析

按照P-M扩散方程的设计思想：扩散系数在光滑区域取值很大，而在边缘区域则取值很小，这样光滑区域的点就会因周围点的平均作用而抑制掉其中所存在的随机性噪声，而边缘区域的点则不会被其周围的点平均掉，所以边缘区域的灰度值基本不变，达到在去噪的同时保持边缘信息的效果。由于Perona和Malik提出的扩散系数的扩散速度很大，在梯度阈值附近仍然存在扩散，故由Perona和Malik给出的扩散系数很可能在扩散的过程中消除一些不太明显而又重要的细节边缘和弱化高对比度的区域。Black M J在1998年给出了各向异性扩散和稳健统计学的联系、稳健估计模型的推导过程和具体含义，并给出了一些具有稳健统计特性的边缘终止函数，其中比较有代表性的是Tukey提出的Biweigh函数（其中k为梯度阈值）：

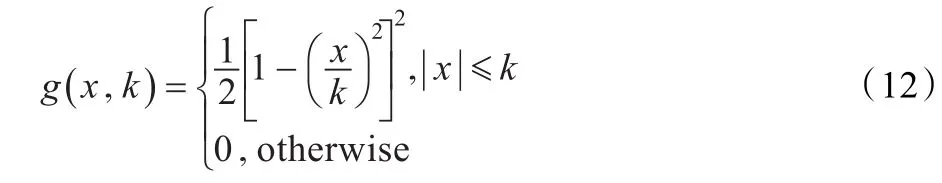
下面将基于Tukey的Biweight扩散系数和Perona-Malik扩散系数（以式（7）为例）与函数图像相结合，分析和比较一下这两个扩散系数及其各自对应的误差模型和影响函数(φ(·))的特性。

从图1和图2中各自的边缘终止函数和它们对应的影响函数可以看到，基于Tukey函数的影响函数比Perona-Malik影响函数递减程度更快，且当梯度超过某一阈值后，影响函数递减为0，即模型不再进行扩散，从而避免了边缘弱化的问题，因此使用基于Tukey函数的边缘终止函数能达到更好地保护图像边缘和细节的效果。

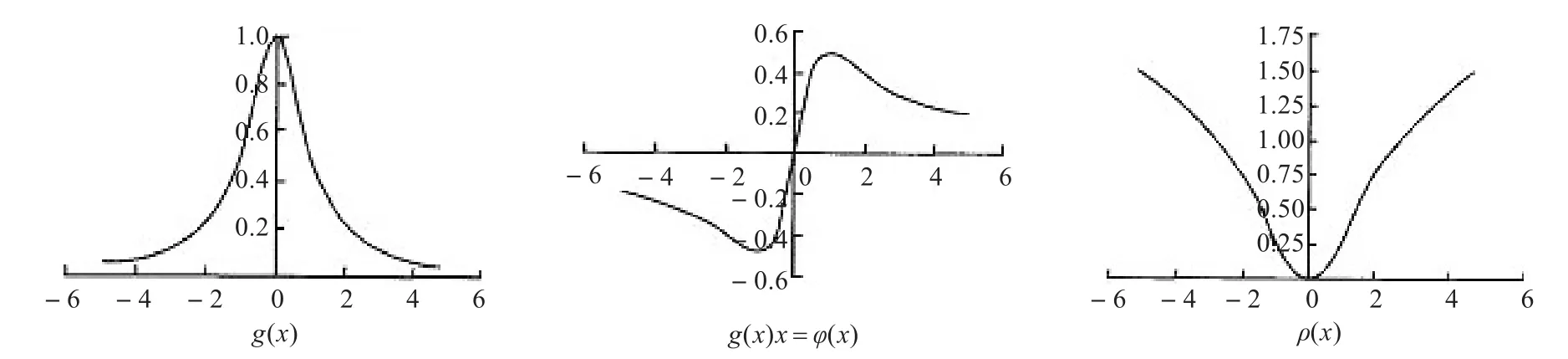
图1 Perona-Malik边缘终止函数、对应的影响函数和稳健统计学误差

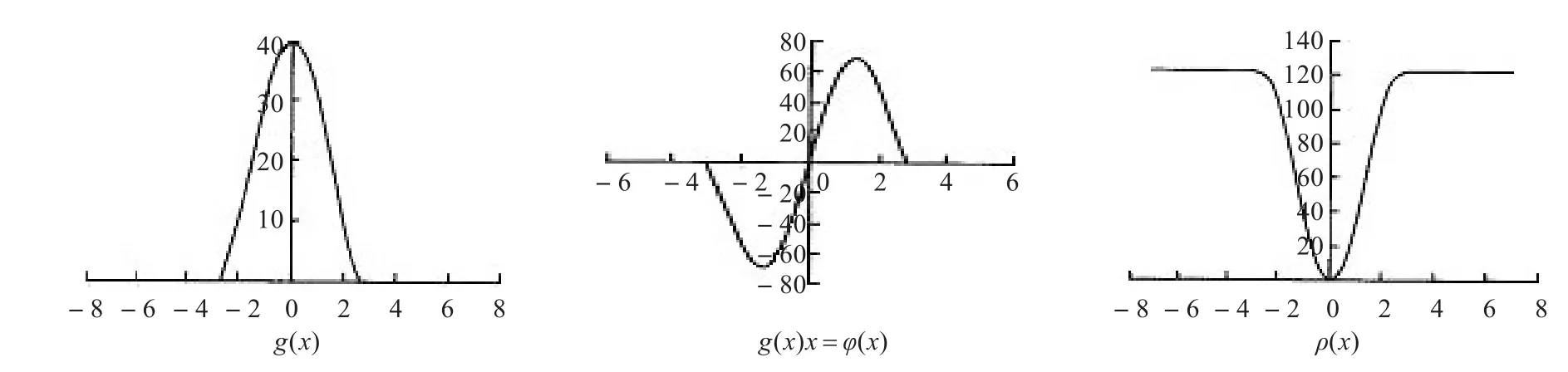
图2 基于Tukey函数的边缘终止函数、对应的影响函数和稳健统计学误差模型

2.3 梯度阈值的非线性衰减

在用P-M扩散方程对带噪图像作去噪处理的过程中，梯度阈值k对于图像中边缘保持有着非常关键的作用。从扩散过程的本质来看，随着扩散的不断进行，图像梯度的绝对值会越来越小。随着梯度绝对值的减小，梯度阈值k也应该相应减小，从而保持图像的边缘不被丢失，因为边缘保持的条件是| ∇I|＞k。

针对这种情况，在仿真中使梯度阈值k随时间变小，即扩散系数变为如下形式：

考虑扩散过程中前后图像的关联性和实现过程中的方便性，给出如下基于递归形式的梯度衰减形式：

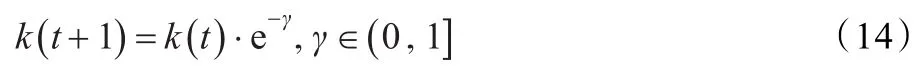
其中可由γ来控制扩散的速度，随着γ的不断变大，退化过程越来越慢。分析上式，可以知道，随着t的增加（即扩散次数的增加），梯度阈值k会不断减小，达到了预期的效果。

2.4 扩散最优停止时间

当P-M扩散方程应用于图像平滑的时候，由于模型中没有考虑处理后图像与原始图像的逼近项，因此利用模型抑制就必须考虑最优停止时间的问题。本文采用相对峰值信噪比来控制扩散的程度，其定义如下：

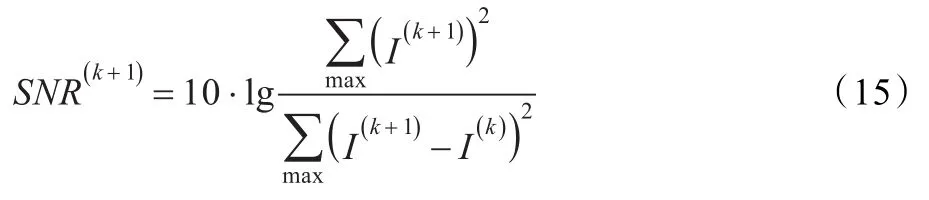
式中I(k)和I(k+1)分别是图像经过第k次和第k+1次迭代滤波后的结果。于是当迭代中止条件

满足时迭代过程中止。

3 新的斑点噪声抑制算法

大量的仿真实验证明，P-M模型对高斯白噪声的处理效果是比较好的。根据SAR图像的噪声特点，结合前面的关于相干斑噪声及其经过对数变换后的统计特性的一些结论，本文选择P-M扩散方程来去除SAR图像的相干斑噪声。综合稳健统计学知识和梯度阈值的非线性退化的思想，本文对P-M扩散方程进行了改进，建立了如下的扩散系数：

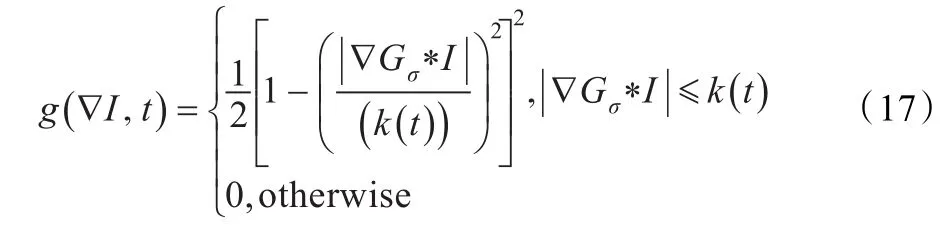
其中，k(t)由式（14）给出。

本文提出的斑点噪声的滤波算法步骤描述如下：

步骤1对原始SAR图像的加性噪声进行抑制：通常原始SAR图像中除了包含乘性的相干斑噪声外，还包含有加性噪声，亦即SAR图像的数学模型为Y=FX+n。因此，在抑制乘性的相干斑噪声之前，首先采用高斯滤波器来对加性噪声n进行抑制。

步骤2对SAR图像作对数变换：利用对数变换= 20lg(Y)将乘性噪声模型转换为加性噪声模型。

步骤3利用改进的P-M方程（18）对对数域图像的加性噪声F~进行抑制，本步骤又分为如下几步：

其中，g(∇I，t)如式（17）。

（1）对对数域图像作如下处理：，这样中的加性噪声′将在理论上趋近于高斯白噪声。

图3 仿真实验1滤波效果

图4 仿真实验2滤波效果

（2）利用改进的P-M模型对进行噪声抑制：在处理之前要确定高斯滤波函数的参数σ，扩散模型的迭代次数N，步长Dt，梯度阈值参数的初始值k(1)以及其衰减系数λ；利用式（9）对Y~进行噪声抑制，其离散化形式如式（19）所示，利用式（15）和式（16）所表示的扩散停止准则来确定扩散的停止时间。

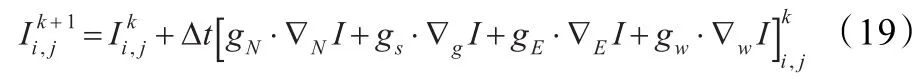
其中N，S，E，W是North，South，East和West的简写，τ为时间步长，符号∇并不是梯度算子，而是表示差分，即

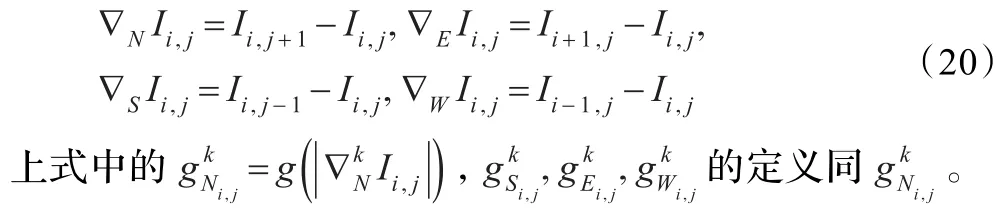
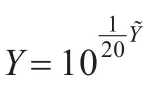
4 实验结果与分析

4.1 实验结果评价指数

国外公共数据库MSTAR数据是公开评价SAR算法性能的标准数据。下面通过对MSTAR数据的实验来验证本文方法的相干斑抑制效果。实验中，分别采用Lee滤波、SRAD滤波和本文方法进行处理。

在对处理结果进行定量评价时，采用图像均值μ、等效视数（ENL）和边界保持指数（EPI）几个评价指标。

均值是衡量图像整体特征的指标，反映图像的平均亮度，处理前后要求均值要基本保持。

等效视数是衡量相干斑的相对强度的一种，定义为：ENL=μ2/σ2，其中μ和σ2分别为图像均匀区域的均值和方差。等效视数越高，表明相干斑抑制越好。

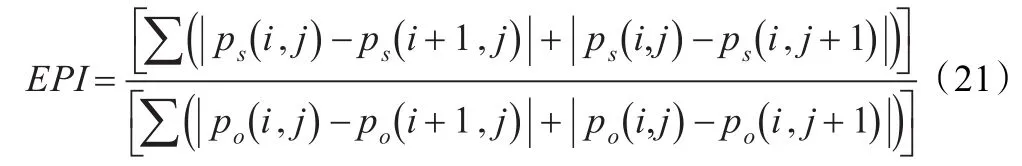
图像的边缘保持指数是衡量算法对图像边缘保持程度的重要指标，其定义为：ps(i，j)是滤波后图像像元，pο(i，j)是原始图像像元，ps(i，j)和pο(i，j)都位于边缘区域，i是行数，j是列数。EPI的取值范围为：0～1，EPI的值为1时图像的边缘得到完全保持，EPI的值为0时，图像已经变为一个平面，没有任何变化。

4.2 实验结果

仿真结果见图3和图4；实验数据见表1和表2。从仿真结果和实验数据可以看出，Lee和SRAD在一定程度上降低了图像的标准差，且等效视数较大；但是在保留边缘细节方面效果不是很好；从视觉效果来说平滑效果也不理想。相比之下，本文提出的算法不仅可以较好地保持均值，大大降低标准差，对均匀区域的平滑效果较好，而且在保持和增强边缘细节方面效果也很明显，所得到的SAR图像有良好的视觉效果。

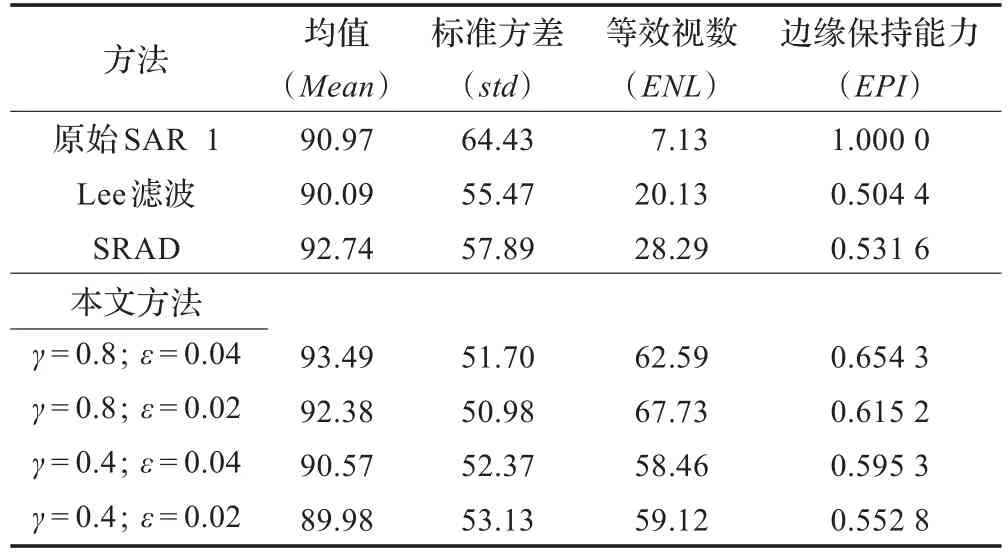
表1 实验结果1

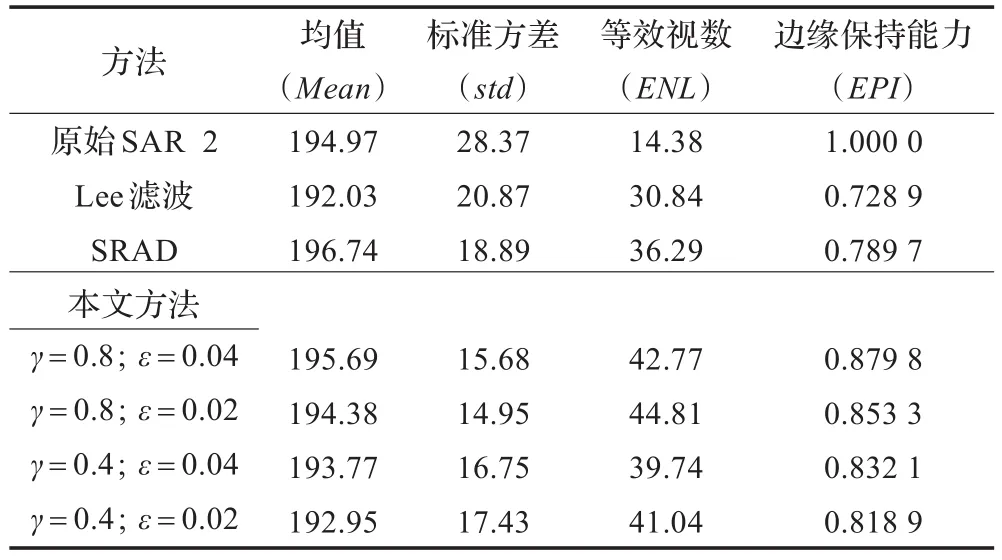
表2 实验结果2

4.3 参数分析

从前面的讨论中可以知道，参数γ和ε的选取对模型的扩散行为有着重要的影响。由图5知，随着参数γ的变大，梯度阈值的非线性衰减越厉害，这样就会对图像的边缘细节保护比较好，EPI会有所升高；但是由于梯度阈值的减小，很多噪声点也被保留下来了，因此ENL会有所下降。由图6知，随着ε的变小，扩散停止时间会增加，这样图像会越来越光滑，ENL有所提高，而EPI值会有所下降。因此在实际的处理过程中要根据实际的应用环境来选择参数γ和ε，以达到更佳的应用效果。

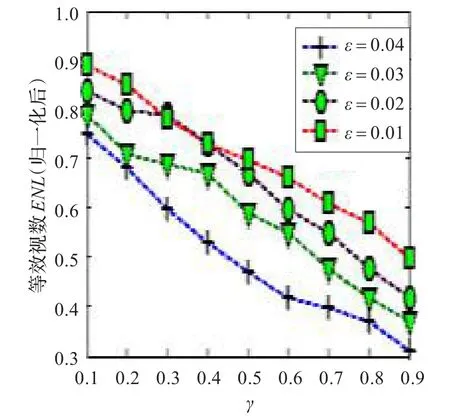
图5 ε和γ对ENL的影响曲线示意图

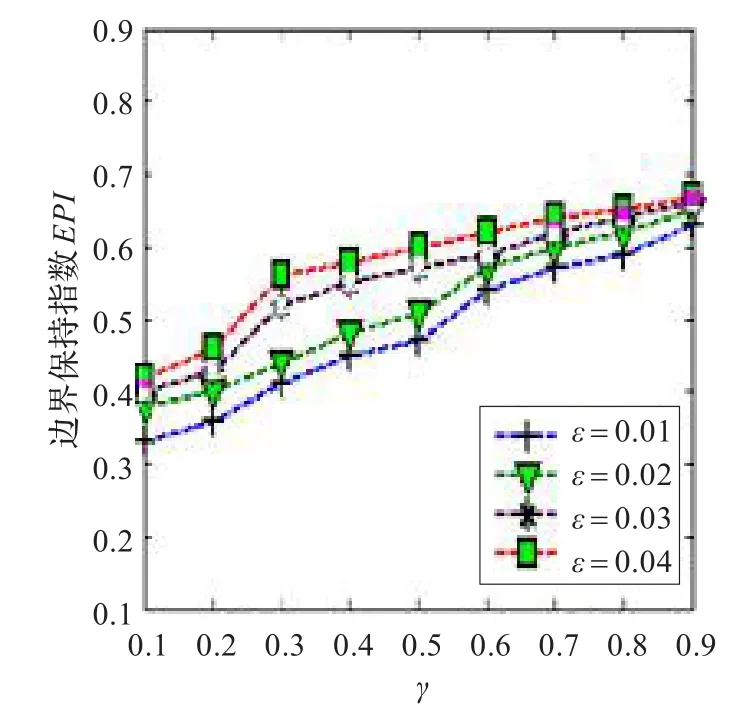
图6 ε和γ对EPI的影响曲线示意图

5 总结

本文提出的相干斑噪声抑制算法是建立在P-M[11]扩散模型和对数变化对相干斑噪声的理论推导之上的。通过透彻分析P-M模型的扩散行为，结合实际仿真环境，对扩散系数、梯度阈值、扩散停止时间的选择等方面进行改进，并给出了详细的算法步骤和实验结果。通过理论分析与实验结果说明该算法在去相干斑和保持边缘等方面都有一定优势。

[1]Lee S J.Digital image enhancement and noise filtering by use of local statistics[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1980，2（2）：165-168.

[2]Frost S V.A model for radar images and its application to adaptive digital filtering of multiplicative noise[J].IEEE Trans on Pattern Analysis and Machine Intelligence，1982，4（2）：157-166.

[3]Kuan T D.Adaptive restoration of images with speckle[J]. IEEE Trans on ASSP，1987，35（3）：373-383.

[4]Lopes，Nezry E，Touzi R，et al.Structure detection and statistical adaptive speckle filtering in SAR images[J].Int J Remote Sensing，1993，14（9）：1735-1758.

[5]Lopes，Touzi R，Nezry E.Adaptive speckle filters and scene hoterogeneity[J].IEEE Transactions on Geoscience and Remoted Sensing，1990，28（6）：992-1000.

[6]Xie H，Pierce L E，Ulaby F T.SAR speckle reduction using wavelet denoising and Markovrandom field modeling[J].IEEE Trans on Geosci Remote Sens，2002，40（10）：2196-2212.

[7]Yu Y J，Action S T.Speckle reduction anisotropic diffusion[J]. IEEE Transactionson ImageProcessing，2002，11（11）：1260-1270.

[8]Aja-Fernandez S，Alberola-Lopez C.On the estimation of the coefficient of variation for anisotropic diffusion speckle filtering[J].IEEE Trans on Image Processing，2006，15（9）：2694-2701.

[9]Black M J，Sapiro G，Marimont D H，et al.Robust anisotropic diffusion[J].IEEE Transactions on Image Processing，1998，7（3）：421-432.

[10]王毅，张良培，李平湘.多光谱遥感图像的自适应各向异性扩散滤波[J].遥感学报，2005，9（6）：659-666.

[11]Ulaby F，Dobson M C.Handbook of radar scattering statistics for terrain[M].Norwood，MA：Artech House，1989.

[12]Perona P，Malik J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1990，12（7）：629-639.

CHEN Shaobo,HOU Jianhua,ZHANG Hua

College of Electronics and Information Engineering,South-Central University for Nationalities,Wuhan 430074,China

The filter based on P-M diffusion equation directly has been proven to be efficient to the additive noise,but it often fails when facing the multiplicative noise（such as the SAR image speckle）.A novel speckle reduction method based on improved P-M diffusion equation is presented.By discussing the influence of applying log transfer to speckle,the theoretical foundation of applying P-M diffusion equation to speckle reduction is provided.A new diffusion coefficients based on Tukey’s Biweight Estimator error norm by recurring to the relationship between robust statistics and P-M diffusion is built.Simultaneously,the nonlinear time-dependent cooling technique for gradient threshold is incorporated into the new diffusion coefficients.In the experiment, the method is proven good performance in reducing speckle noise and preserving edges and details at the same time.Moreover, the filtered SAR images look good.

speckle;log-transform;Perona-Malik（P-M）diffusion equation;robust statistics;gradient threshold

直接基于Perona-Malik扩散方程的滤波算法对于加性噪声非常有效，但是对于乘性噪声（如合成孔径雷达（SAR）图像相干斑噪声）收效甚微。提出了一种基于改进的Perona-Malik扩散方程抑制SAR图像相干斑噪声的新算法。分析对数变化对相干斑噪声的影响，为将P-M扩散方程应用于相干斑噪声抑制奠定了理论基础；通过P-M扩散和稳健统计学的联系，建立了基于Biweight Estimator误差模型的扩散系数；同时利用非线性衰减技术对梯度阈值的选择改进。实验表明，该方法不仅有效抑制了SAR图像相干斑噪声，较好地保持了细节和边缘信息，而且视觉效果比较好。

相干斑；对数变换；P-M扩散方程；稳健统计；梯度阈值

A

TN911.73

10.3778/j.issn.1002-8331.1303-0403

CHEN Shaobo,HOU Jianhua,ZHANG Hua.Application of improved P-M diffusion equation in speckle reducing. Computer Engineering and Applications,2013,49（18）：1-5.

国家自然科学基金（No.61201448）；湖北省自然科学基金（No.2011CHB043）；武汉市科技攻关项目（No.201212521825）；中南民族大学中央高校基本科研业务费专项资金项目（No.CZY10001）。

陈少波（1980—），男，博士，讲师，研究方向：图像去噪、字符识别；侯建华（1964—），男，博士，教授；张华（1972—），男，博士，讲师。E-mail：chenshaobo1980@qq.com

2013-03-26

2013-05-17

1002-8331（2013）18-0001-05

CNKI出版日期：2013-06-08 http://www.cnki.net/kcms/detail/11.2127.TP.20130608.1001.029.html