模糊动态联盟收益分配改进算法

张艳菊，赵宝福

辽宁工程技术大学 工商管理学院，辽宁 葫芦岛 125105

模糊动态联盟收益分配改进算法

张艳菊，赵宝福

辽宁工程技术大学 工商管理学院，辽宁 葫芦岛 125105

考虑到实际生活中动态联盟收益具有模糊性，则联盟的收益分配问题实质是模糊合作博弈解的求解问题。

对模糊合作博弈的研究主要集中在两方面：（1）仅参与度模糊的模糊合作博弈（也称为联盟模糊的模糊合作博弈）。Aubin[1-3]提出了局中人可以用[0，1]之间的模糊数表示参与度参加某个或某几个联盟，继而正式提出了模糊合作博弈的概念；Butnariu[4-7]对模糊Shapley值给出了定义，但是该定义未能很好地满足现实的应用需求。Tsurumi[8]在前人研究的基础上构造了一个具有Choquet积分的模糊Shapley值，该构造既单调非减又连续。逄金辉[9]等考虑了局中人的联盟隶属度的动态变化，将隶属度表示为介于[0，l]区间的三角模糊数，该研究回避了模糊被测函数下的Choquet积分计算过程中一个重要的问题，即不同置信水平下模糊隶属度截集的排序问题。（2）仅具有模糊支付的模糊合作博弈。主要成果：Mares[10-12]指出带有模糊支付的合作博弈也是模糊合作博弈的一种形式。按照传统的Shapley值定义了模糊Shapley值。但是，他定义的模糊Shapley值无法满足Shapley提出的三条公理。Arts[13]等1997年从集合论的角度，研究了合作博弈的Shapley值，使模糊Shapley值得到了拓展和延伸。孟凡永，张强[14]定义了模糊支付下具有Choquet积分形式的模糊合作博弈，提出了该模糊合作博弈下具有Choquet形式的Shapley值。该研究本质上是带模糊支付的合作博弈。于晓辉，张强[15]拓展了传统Shapley函数满足的三条公理，提出了联盟支付为区间数的Shapley函数形式。该研究为本文的研究起到一定的启发作用。

在模糊环境下研究动态联盟收益分配问题，将动态联盟的预期收益视为模糊数，采用模糊合作博弈来研究该问题非常必要。这就对模糊合作博弈提出了更高的要求。由于以往基于扩张原理的模糊数的运算存在遍历性，模糊Shapley值的隶属函数表达非常复杂，以上研究方法未能准确地描述出模糊合作博弈的Shapley值的隶属函数及给出合理的动态联盟收益分配方案。本文应用模糊结构元理论[16-20]，改进模糊Shapley值的算法，使模糊Shapley值的隶属函数得到解析表达。采用新算法来研究动态联盟收益分配问题，与其他研究方法相比，该算法体现决策者行为偏好对收益分配的影响，更加准确、易操作、易推广。具有良好的理论价值和应用价值。

1 传统合作博弈的Shapley值

合作博弈是局中人在竞争中为取得自己的最大利益而进行决策分析的模型。在合作博弈的过程中，局中人需要考虑如何结成联盟及如何分配合作所取得的收益。

二元组(I，v)称为局中人集合I={1，2，…，n} 上的合作对策，如果v是I的所有子集形成的集合2I上的映射，即v:2I→R满足：

（1）v(Φ)=0；

（2）对于K，L⊂I且K∩L=Φ，则有v(K∪L)≥v(K)+v(L)。

映射v称为支付函数，I的任意子集K称为联盟。从测度论的观点看，v是集合2I上的一个超可加集函数。

合作博弈有多个解的定义，Shapley值是其中之一，也是最常用的一种解概念。1953年，Shapley提出了一种求解多人合作博弈问题的公理化方法[21-22]，其提出了三个人们普遍接受的公理。

公理1（对称性）如果局中人i，j∈I，对于任意的联盟K⊂I{i，j}总有v(K∪{i})=v(K∪{j})，那么φi(v)=φj(v)。

公理3（可加性）对于任意两个合作对策(I,v1)和(I,v2)，如果存在一个合作对策(I，v1+v2)，对于任意的联盟K⊂I总有(v1+v2)×(K)=v1(K)+v2(K)，则φi(v1+v2)=φi(v1)+φi(v2)，i∈I。

然后，求出唯一满足这三个公理的各局中人的支付值φi(v)→R，

其中，k为联盟K中的人数，n为局中人的个数。φ(v)= (φi(v))i∈I为Shapley值向量，简称Shapley值，它是支付函数v的单调非减函数，在满足超可加性的合作博弈中表示某一确定的分配。

2 模糊数的模糊结构元表示

设E为实数域R上的模糊集，隶属函数记为E(x)，x∈R。如果E(x)满足下述性质：（1）E(0)=1；（2）在区间[-1，0)上E(x)是单增右连续函数，在区间(0，1]上是单降左连续函数；（3）当x＜-1或者x＞1时，E(x)=0，则称E为R上的模糊结构元。

若模糊结构元E满足：（1）∀x∈(-1，1)，E(x)＞0；（2）E(x)连续，且在[-1，0)上严格单增，在(0，1]上严格单降，则称E为正则的；若E(-x)=E(x)，称E为对称的。

定理1[19]设E是R上的任意模糊结构元，具有隶属函数E(x)，f(x)是[-1，1]上单调有界函数，则f(E)是R上有界闭模糊数。反之，对于给定的正则模糊结构元E和任意的有界闭模糊数，总存在一个[-1，1]上的单调有界函数f，使得，称模糊数是由模糊结构元E生成的。

定理2[19]若模糊数，则的隶属函数为E(f-1(x))，这里f-1(x)是f(x)关于变量x和y的轮换对称函数（若f(x)是连续严格单调的，则f-1(x)是f(x)的反函数）。

上述定理的证明可参见文献[16-20]。

只要取：

用D[-1，1]表示区间[-1，1]上的同序单调有界函数全体，定义D[-1，1]上的几个同序单调变换τi:D[-1,1]→D[-1，1]，i=0，1，2，3，∀f∈D[-1，1]，定义：

定理3[19]设E是对称模糊结构元，如果f和g是[-1，1]上两个同序单调函数（不妨假定都是单调增函数），模糊数A=f(E)，B=g(E)，是f的同序变换，则有如下结论：

（1）若A和B是任意有界模糊数，则A+B=(f+g)(E)，具有隶属函数：

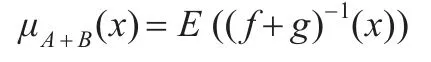
（2）若A和B是任意有界模糊数，具有隶属函数：

（3）若A和B都是正模糊数，则AB=f(E)·g(E)= [f·g](E)，具有隶属函数：

（4）若A和B都是负模糊数，则，具有隶属函数：

（5）若A是负模糊数，B是正模糊数，则，具有隶属函数：

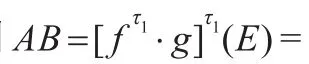
（6）若A和B都是正模糊数，且B的承集不包含0，则

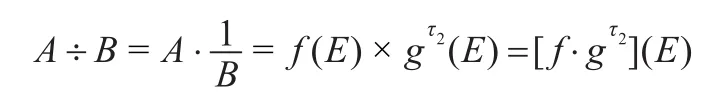
具有隶属函数：

（7）若A和B都是负模糊数，且B的承集不包含0，则

具有隶属函数：

（8）若A是负模糊数，B是正模糊数，且B的承集不包含0，则

具有隶属函数：

3 具有模糊支付动态联盟合作博弈的模糊Shapley值的结构元表示

3.1 具有模糊支付的模糊合作博弈及其模糊Shapley值

记局中人集合为N，N中的所有清晰联盟和模糊联盟分别记为P(N)和L(N)。对P(N)中的清晰联盟记为S0，T0，…，它们的基数分别表示为s，t，…，L(N)中的模糊联盟记为S，T，…对任意的i∈N和S∈L(N)，记S(i)为局中人i在模糊联盟S中的隶属度。将S0∪{i}，S∪{U(i)}分别简记为S0∪i，S∪U(i)，其中S∪U(i)表示局中人i以参与水平U(i)加入模糊联盟S0任意的模糊联盟S∈L(N)，其支集记为supp S={i∈N|S(i)＞0} 。对任意h∈[0，1]，记[S]h={i∈N|S(i)≥h}为模糊联盟S的h水平集。若函数满足：，则称上的具有模糊支付的合作博弈，其全体记为

证明详见参考文献[14]。

3.2 模糊Shapley值的结构元表示

本文设E是对称模糊结构元，如果f是[-1，1]上同序单调函数（不妨假定都是单调增函数），模糊数是f的同序变换，则有如下定理：

定理5模糊合作博弈中局中人所得支付的Shapley值是一个模糊数，求出唯一满足这三个公理的各局中人的支付值n其隶属函数为：

3.3 结构元线性生成的模糊Shapley值表达式

结论1求出唯一满足这三个公理的各局中人的支付值

其隶属函数为：

证明因为

根据定理3得到：

所以

又根据定理3得：

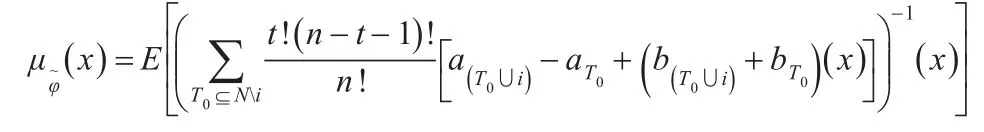
4 动态联盟收益分配运算示例

在动态联盟企业中，各盟友充分利用自身的核心能力进行优化整合，以追求整体经济利益的最大化。这样联盟伙伴的优化组合过程可以看做是n人合作博弈过程，联盟伙伴的收益分配可以看做是n人合作博弈的收益分配问题。

假设局中人a1，a2，a3三家企业欲合作汽车零部件联合研发项目，如果局中人独立研发，则均可获利约为5亿元，如果a1，a2合作研发可获利约为35亿元，如果a1，a3合作研发可获利约为25亿元，如果a2，a3合作研发可获利约为20亿元，如果a1，a2，a3合作研发可获利约为50亿元，上述预期收益用三角模糊数表示为：

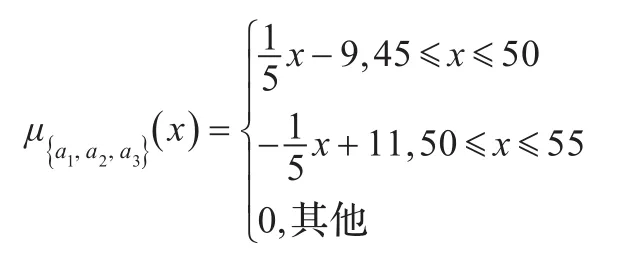
解：这里取E为三角结构元，其隶属函数为：

根据定理5，计算局中人a1的模糊合作博弈的Shapley值，计算过程如下：

同理可求得局中人a2，a3的Shapley值，分别为：

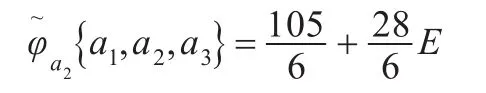
其隶属函数为：

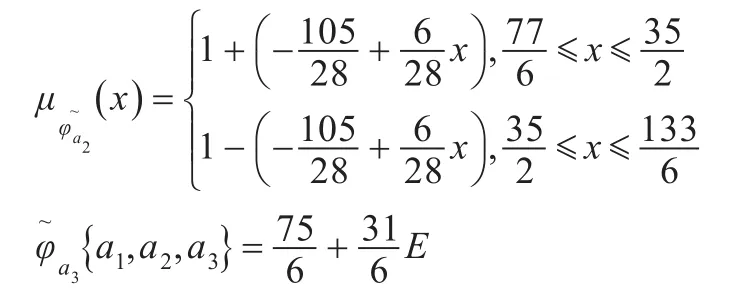
其隶属函数为：

以局中人a1为例，可以计算得到不同联盟组合下的a1收益分配，a1单干时，a1可获利，其隶属函数为：

a1，a2联合时，a1可获利：

其隶属函数为：

a1，a3联合时，a1可获利：

其隶属函数为：

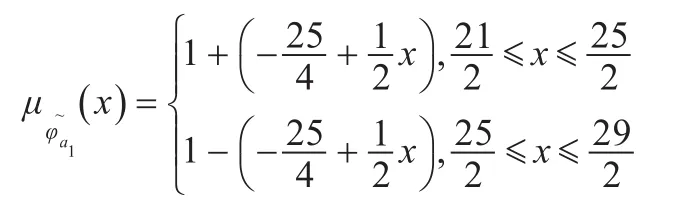
a1，a2，a3联合时，a1的获利前面计算已求得。

则局中人a1选取的合作策略是与局中人a2，a3共同结成联盟。同理，局中人a2，a3通过类似的方法得到联盟{a1，a2，a3}是他们的最优策略。这样，联盟{a1，a2，a3}就组建了。

现讨论联盟收益如何分配。若联盟{a1，a2，a3}实际收益51亿元，代入联盟的隶属函数可知，隶属度为0.8。再将0.8代入三家企业各自的收益隶属函数（将0.8代入核心右侧）可得三家企业偏好程度为0.8时的Shapley值分别为：21.03，18.43，12.87。按照这个比例去分配收益51亿元，可得三家企业分别收益20.495 51亿元、17.961 59亿元，12.542 90亿元。

该方法比文献[23]的结果精确，比文献[24]的计算方法简单，该改进算法更加形象、准确、易操作、易推广。

5 结论

本文在前人对具有模糊支付的合作博弈研究基础上，应用模糊结构元理论，改进模糊Shapley值算法，使模糊Shapley值的隶属函数得到解析表达。考虑到现实生活中，动态联盟的预期收益具有模糊性，采用改进算法来研究动态联盟收益分配问题，与其他研究方法相比，该算法清晰地体现出决策者行为偏好对收益分配的影响，更加准确、易操作、易推广。具有良好的理论价值和应用价值，可以为管理者提供更精确的信息。

[1]Aubin J P.Coeur et valeur des jeux flous paiements lat raux[C]//ComptesRendusHebdomadairesdesSancesde 1’Acadmie des Sciences，1974，279-A：891-894.

[2]AubinJ P.Mathematical methods of game andeconomic theory[M].Amsterdam：North-Holland Press，1980.

[3]Aubin J P.Cooperative fuzzy games[J].Mathematical Operation Research，1981，6：1-13.

[4]Butnariu D.Fuzzy games：a description of the concept[J]. Fuzzy Set and System，1978，1：181-192.

[5]Butnariu D.Stability and Shapley valueforann-persons fuzzy games[J].Fuzzy Set and System，1980，4：63-72.

[6]Butnariu D，Klement E P.Triangular norm-based measures and games wih fuzzy coalitions[M].Dordrecht：Kluwer Press，1993.

[7]Butnariu D，Klement E P.Core，value and equilibria for market games：on a problem of Aumann and Shapley[J].International Journal of Game Theory，1996，18：149-160.

[8]Tsurumi M，Tanino T，Inuiguchi M.A Shapley functicn on a class of cooperative fuzzy games[J].European Journal of Operational Research，2001，129：596-618.

[9]逄金辉，陈秋萍.基于模糊机会约束的博弈联盟收益[J].北京理工大学学报，2010，30（11）：1383-1386.

[10]Mares M.Fuzzy coalition forming[C]//Proceedings of 7th IFSA World Congress，Prague，1997：70-73.

[11]Mares M.Fuzzy Shapleu value[C]//Proceedings of Transactions of IPMU 2000，Madrid，2000：1368-1372.

[12]Mares M.Fuzzy cooperative games：cooperation with Vague expectations[M].New York：Physica-Verlag Press，2001.

[13]Arts H，Hoede C，Funaki Y.A marginalistic value for monotonic set games[J].International Journal of Game Theory，1997，26：97-111.

[14]孟凡永，张强.具有Choquet积分形式的模糊合作对策[J].系统工程与电子技术，2010，32（7）：1430-1436.

[15]于晓辉，张强.模糊合作对策的区间Shapley值[J].中国管理科学，2007，15（z1）：76-80.

[16]郭嗣琮.模糊分析中的结构元方法（I）[J].辽宁工程技术大学学报，2002，21（5）：670-673.

[17]郭嗣琮.模糊分析中的结构元方法（II）[J].辽宁工程技术大学学报，2002，21（6）：808-810.

[18]郭嗣琮.模糊实数空间与[-1，1]上同序单调函数类的同胚[J].自然科学进展，2004，14（11）：1318-1321.

[19]郭嗣琮.[-1，1]上同序单调函数的同序变换群与模糊数运算[J].模糊系统与数学，2005，19（3）：105-110.

[20]Guo Sizong.Fuzzy analysis and calculate based on structured element[C]//Proceedings of the 6th International FLINS Conference on Applied Compuational Intelligence.[S.l.]：World Scientific Publishing Co.Pte.Ltd.，2004：128-134.

[21]Shapley L S.A value forn-persons games[J].Annals of Mathematics Studies，1953，28：307-318.

[22]Aumann R J，Shapley L S.Values of non-atomic games[M]. Princeton：Princeton University，1974.

[23]陈雯，张强.模糊合作对策的Shapley值[J].管理科学学报，2006，9（5）：50-55.

[24]刘天虎，许维胜，吴启迪.基于动态模糊联盟合作博弈的区间模糊Shapley值[J].计算机工程与应用，2008，44（14）：13-17.

ZHANG Yanju,ZHAO Baofu

School of Business Administration,Liaoning Technical University,Huludao,Liaoning 125105,China

Dynamic coalition focuses on cooperation between the Leaguers,and the profit allocation is the result of cooperation rational participation.Taking into account the fuzziness of the profit allocation,this paper applies fuzzy cooperative games to solving the dynamics coalition.The key problem is to solve the Shapley value of fuzzy cooperative game.The fuzzy structured element theory is applied to analyzing fuzzy cooperative games.Then membership function of the fuzzy Shapley value can get analytic expression.The method can embody different dynamic profit distribution under different behavior preference,and the results of application verify the effectiveness of the improved algorithm.

fuzzy mathematics;structured element;cooperative games;dynamics coalition

动态联盟注重盟员间的合作，在参与人合作过程中，收益分配是其理性选择的结果。实际生活中收益又具有模糊性，所以应用模糊合作博弈来研究该问题非常必要。这里的关键问题是模糊合作博弈Shapley值的求解问题。将模糊合作博弈中的模糊支付用模糊结构元表示，给出基于结构元理论的各局中人Shapley值求解方法，使其得到解析表达。求解该方法可以体现出决策者不同行为偏好下动态收益的不同分配，应用结果验证了改进算法的有效性。

模糊数学；结构元；合作博弈；动态联盟

A

O159

10.3778/j.issn.1002-8331.1305-0089

ZHANG Yanju,ZHAO Baofu.Improved algorithm of fuzzy dynamic alliance profit distribution.Computer Engineering and Applications,2013,49（18）：6-10.

葫芦岛市科技局研究项目；深圳市世贸组织事务中心研究项目。

张艳菊（1983—），女，博士研究生，研究方向：模糊决策理论与应用，区域经济学等；赵宝福（1957—），通讯作者，男，教授，博士生导师，研究方向：模糊决策理论与应用，区域经济学股份制经济等。E-mail：juzi2002@126.com

2013-05-13

2013-06-14

1002-8331（2013）18-0006-05