非线性互补问题的光滑化拟牛顿算法

牛潇萌

赤峰学院 数学与统计学院，内蒙古 赤峰 024000

非线性互补问题的光滑化拟牛顿算法

牛潇萌

赤峰学院 数学与统计学院，内蒙古 赤峰 024000

1 引言

设F:Rn→Rn是一非线性映射，非线性互补问题（简记为NCP（F））是指：求一个向量x∈Rn，使得：

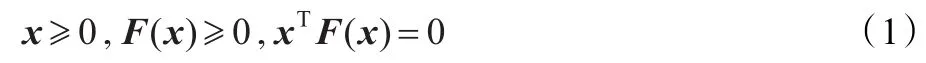
非线性互补问题在很多领域都有重要应用[1-3]，其理论和算法的研究在近些年来得到了长足发展[1]。很多求解NCP（F）的有效算法已被提出[3]，其中比较流行的方法之一是首先把NCP（F）转化成一个非线性方程组H(x)=0，然后利用求解方程组的相关方法[4]间接求解得到NCP（F）的解。牛顿型方法是求解非线性互补问题的一类重要的数值迭代算法，其局部收敛性的研究取得了很好的成果[1]。近些年来，此类算法的全局收敛性研究也得到了诸多进展[5-9]。然而对于计算上更为实用的拟牛顿算法的研究相对较少。其主要困难在于即使对于光滑的非线性方程组，拟牛顿法产生的方向不能保证是某个度量函数的下降方向，常用的线搜索（如Armijo型线搜索）此时已不适用[10]。另外对拟牛顿法来说，那些需要计算导数的线搜索是不适合的。因此，为了得到求解非线性方程组的拟牛顿法的全局收敛性，需要一个无导数线搜索（Derivative-Free Line Search）。

1986 年，Griwank[11]首先提出了一种无导数线搜索，并证明了求解非线性方程组的Broyden秩一校正方法在该线搜索下的全局收敛性，但此线搜索在某些情况下，可能不能实现[12]。Li和Fukushima在文献[12]中，针对文献[11]中无导数线搜索的不足，提出了一个新的易于实现的无导数线搜索。

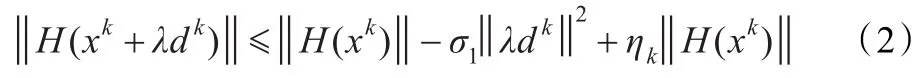
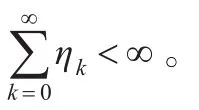
2 光滑对称扰动Fischer-Burmeister函数

使用如下光滑函数[13]：

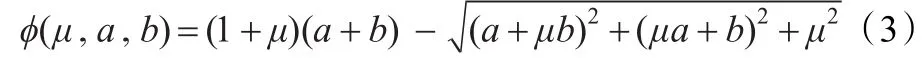
其中(μ，a，b)∈R3，它是通过光滑化对称扰动的Fischer-Burmeister函数：

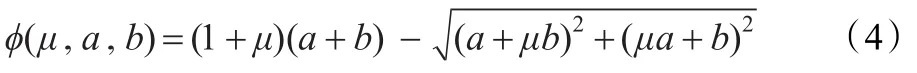
而得到的。

设z=(μ，x)∈Rn+1且

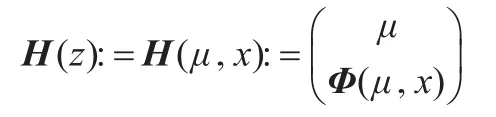
其中：

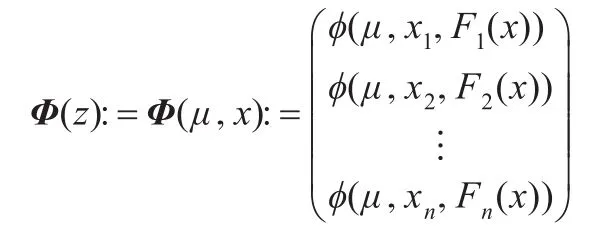
易知H(z)=0⇔μ=0，x是NCP（F）的解。

H(z)的Jacobian矩阵为：

3 光滑化拟牛顿算法

设γ∈(0，1)。定义函数ρ:Rn+1→R+为：

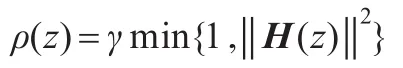
算法：

步骤1选择常数设，任取初始点x0∈Rn。设z0= (μ0，x0)。选择γ∈(0，1)，使得γμ0＜1。设η＞0是一个给定常数并选择一正数列{ηk}满足：

选一个初始非奇异矩阵B0∈Rn×n。设k=0。

步骤2若‖H(zk)‖=0，停。否则，设ρk:=ρ(zk)。若μk＞ρkμ0，解下面的方程得Dzk=(Dμk，Dxk)。

否则，令Dzk=(Dμk，Dxk):=(0，Dxk)，并解如下方程组得Dxk，

其中Gk∈R(n+1)×(n+1)定义为：

且Bk是∇xΦ(zk)T的一个近似。

步骤3若

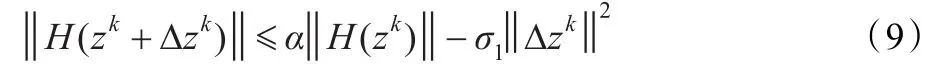
则设λk:=1，转步骤5。

步骤4设λk是取自集合{1，δ，δ2，…}使得λ=δi满足如下线搜索的最大数：

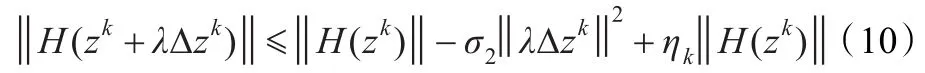
步骤5

步骤6用如下Broyden-like校正公式修正Bk得Bk+1：

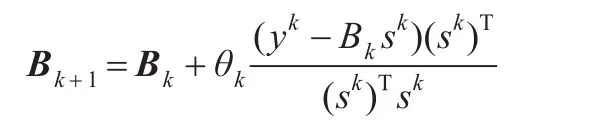
其中sk=λkDxk=xk+1-xk，yk=Φ(μk，xk+1)-Φ(μk，xk)，参数θk满足且Bk+1非奇异。

步骤7令k=k+1，转步骤2。

对算法的说明：

由方程（6）求Dzk分两步：首先由下面的方程求Dμk：

然后解如下线性方程组求Dxk：

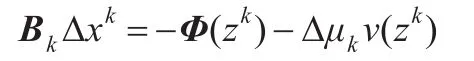
定理1算法是有定义的，且产生一无穷序列{zk=(μk,xk)}满足{μk}⊂R++是单调非增的。

证明由Bk非奇异知Gk+1非奇异，因此线性方程组（6）和（7）唯一可解。易知对充分小的λ＞0，不等式（10）成立。事实上，当λ→0时，式（10）的左边趋于‖H(zk)‖，但右边趋于(1+ηk)‖H(zk)‖。因此算法是有定义的。

下面用归纳法证明{μk}⊂R++。因为μ0＞0，假设μk＞0，则‖H(zk)‖≠0，从而：

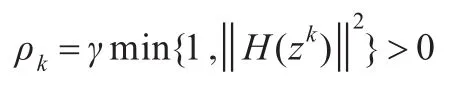
如果μk＞ρkμ0，由式（11）和λk∈(0，1]知：

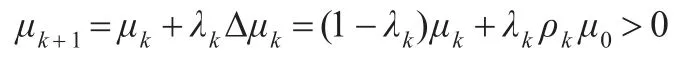
如果μk≤ρkμ0，由算法步骤2可知此时如果Dμk=0，从而μk+1=μk＞0。所以{μk}⊂R++。故算法产生一无穷序列。

下面证明{μk}是单调非增序列。

事实上，如果μk＞ρkμ0，由式（11）知Dμk＜0，从而μk+1=μk+λkDμk＜μk。

如果μk≤ρkμ0，由算法步骤2可知Dμk=0从而μk+1=μk。

所以{μk}是单调非增序列。

4 数值实验结果

算法中相关参数取α=0.9，δ=0.9，σ1=0.8，μ0=10-3，γ= 0.2，η=0.5。程序中取ε=10-6为结束准则，当‖H(zk)‖ ≤ε时终止。

算例1（Josephy问题[14]）求解如下4维非线性互补问题NCP（F），其中F(x)定义如下：

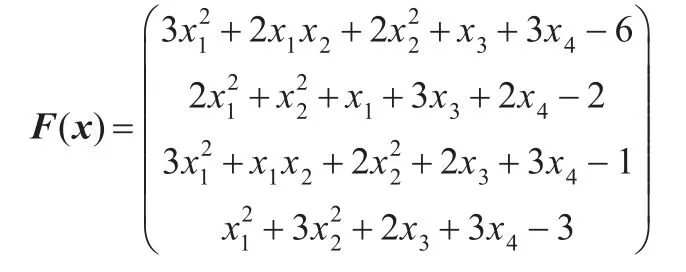
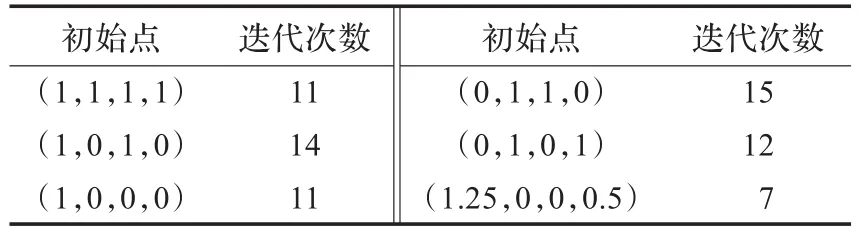
表1 算例1的计算结果

算例2（Murty问题[15]）这是一组n维线性互补问题，设F(x)=Μx+q，n阶方阵M和n维向量q定义如下：

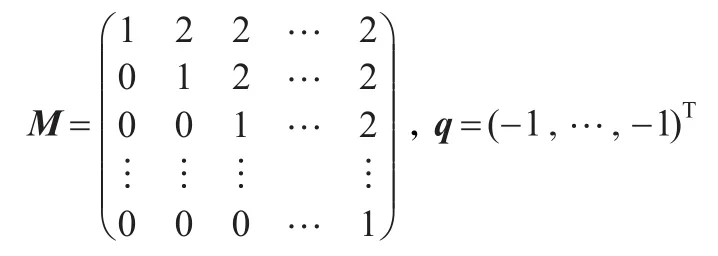
唯一解x*=(0，…，0，1)T。

取初始点x0=(0，…，0)T，计算结果见表2。

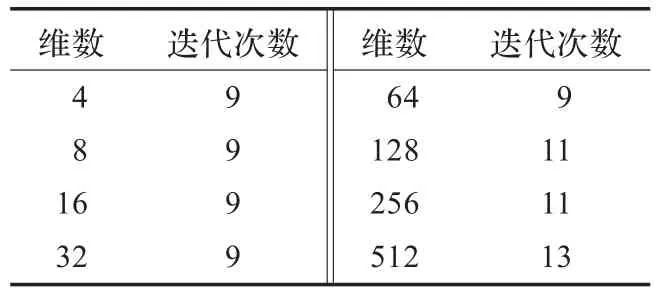
表2 算例2的计算结果

算例3（Kojshin问题[14]）求解如下非线性互补问题NCP（F），其中F(x)定义如下：

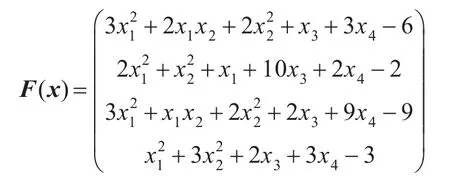
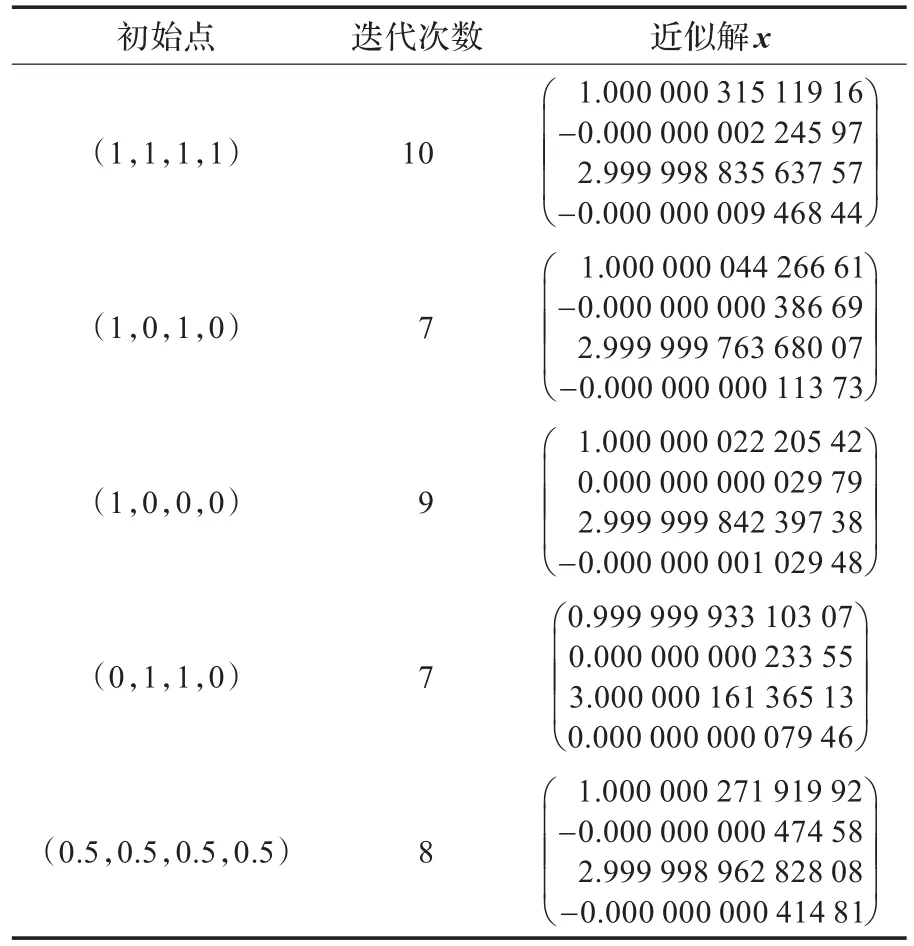
表3 算例3的计算结果

5 结论

基于光滑对称扰动函数并利用无导数线搜索给出了求解P0函数非线性互补问题的光滑化拟牛顿算法。数值结果表明该算法有效，可靠。

[1]Harker P T，Pang J S.Finite-dimensional variational inequality and nonlinear complementarity problems：a survey of theory，algorithms and applications[J].Mathematical Programming，1990，48：161-220.

[2]Ferris M C，Pang J S，Engineering and economic applications of complementarity problems[J].SIAM Review，1997，39：669-713.

[3]韩继业，修乃华，戚厚铎.非线性互补理论与算法[M].上海：上海科学技术出版社，2006.

[4]Dennis J E，Schnabel R B.Numerical methods for unconstrained optimization and nonlinear equations[M].Englewood Cliffs：Prentice-Hall，1983.

[5]Pang J S，Chen D.Iterative methods for variational and complementarity problems[J].Mathematical Programming，1982，24：284-313.

[6]Chen C，Manasarian O L.A class of smoothing functions for nonlinear and mixed complementarity problems[J].Comput Optim Appl，1996，5：97-138.

[7]Jiang H Y，Qi L Q.A new nonsmooth equations approach to nonlinear complementarity problems[J].SIAM J Control Optim，1997，35：178-193.

[8]Chen X，Qi L，Sun D.Global and superlinear convergence of the smoothing Newton method and its application to general box constrained variational inequalities[J].Mathematics of Computation，1998，67：519-540.

[9]Qi L Q，Chen X J.A globally convergent successive approximation method for severely nonsmooth equations[J].SIAM J Control Optim，1995，33：402-418.

[10]Li D H，Fukushima M.A globally and superlinearly convergence Gauss-Newton-based BFGS method for symmetric nonlinear equations[J].SIAM Numer Anal，1999，37：152-172.

[11]Griewank A.The“global”convergence of Broyden-like methods with a suitable line search[J].Journal of Australia Mathematical Society Ser.B，1986，28：75-92.

[12]Li D H，Fukushima M.A derivative-free line search and global convergence Broyden-like method for nonlinear equations[J].Optimization Methods and Software，2000，13：181-201.

[13]Huang Z，Han J，Xu D，et al.The non-interior continuation methods for solving theP0-function nonlinear complementarity problem[J].Science in China，2001，44：1107-1114.

[14]Dirkse S P，Ferris M C.MCPLIB：a collection of nonlinear mixed complementarity problems[J].Optimization Methods and Software，1997，5：123-156.

[15]Kanzow C.Some noninterior continuation methods for linear complementarity problems[J].SIAM Journal on Matrix Analysis and Applications，1996，17：851-868.

NIU Xiaomeng

School of Mathematics and Statistics,Chifeng University,Chifeng,Inner Mongolia 024000,China

To solve nonlinear complementarity problem,a new smoothing quasi-newton algorithm based on the smoothing symmetric perturbed Fischer-Burmeister function is put forward.The algorithm makes use of the derivative-free line search rule.Numerical results indicate this algorithm is efficient.

nonlinear complementarity problem;quasi-newton algorithm;smoothing approximation

为求解非线性互补问题，给出了一种新的基于光滑对称扰动Fischer-Burmeister函数的光滑化拟牛顿算法。该算法利用了无导数线搜索。数值实验表明，算法是有效的。

非线性互补问题；拟牛顿算法；光滑逼近

A

O224

10.3778/j.issn.1002-8331.1205-0118

NIU Xiaomeng.Smoothing quasi-newton for nonlinear complementarity problem.Computer Engineering and Applications, 2013,49（18）：33-35.

牛潇萌（1982—），女，讲师，研究领域为最优化。E-mail：ndnxm@126.com

2012-05-16

2012-07-16

1002-8331（2013）18-0033-03

CNKI出版日期：2012-08-16 http://www.cnki.net/kcms/detail/11.2127.TP.20120816.1045.010.html