图像滤波的商空间粒计算算法

高正龙，吴涛，2，陈小波，杨莹莹

1.安徽大学数学科学学院，合肥 230601

2.安徽大学数学科学学院安徽大学智能计算与信号处理教育部重点实验室，合肥 230601

图像滤波的商空间粒计算算法

高正龙1，吴涛1，2，陈小波1，杨莹莹1

1.安徽大学数学科学学院，合肥 230601

2.安徽大学数学科学学院安徽大学智能计算与信号处理教育部重点实验室，合肥 230601

1 引言

数字图像在采集和传输的过程中，传感器和传输通道经常会发生噪声。噪声的存在严重影响了图像质量，使得后续的图像分割、特征提取、模式识别、图像融合等变得难以实现，因此对噪声图像进行必要的滤波就显得尤为重要。近年来人们根据图像噪声的特点、规律，提出了各式各样的去噪方法，主要是基于空间域去噪方法、变换域去噪方法和一些新兴的图像噪声滤波器并取得了明显的效果[1-8]。然而这些方法在噪声检测过程中主要是基于固定窗口大小或给定窗口中检测的方向，容易造成噪声的漏检、误检或增加了运算代价；基于K-SVD[7]的滤波算法（K-SVDF）对频域变换产生的冗余字典进行训练，以便形成能够有效反映图像结构特征的超完备字典[8]，然后再进行滤波，尽管该算法能实现高效滤波，但训练速度较慢。商空间理论模拟人依不同粒度进行思维的能力，讨论论域、属性、结构在不同粒度下的表示、性质以及这些表示、性质之间的相互依存、相互转换的关系，将问题放在各种不同粒度的空间（商空间）上进行分析研究，然后综合得出对原问题的解，提高问题求解效率[9]。本文基于该理论，构造了粒度噪声检测器和粒度逆谐波均值滤波器，首先将待检测的噪声图像分割不同的粒度窗口，形成商空间簇，并在此粒度下对每个窗口实施检测，然后结合保假原理判断是否需要再划分到细粒度空间中进行判断，最后对已检测为噪声粒度空间中的噪声点实施分类标记和滤除。从而较好地避免了噪声检测过程中噪声点之间的相互干扰、噪声点滤除方式的单一，很好地解决了传统方法在噪声滤波中存在的不足。实验结果表明，本文算法除了具有较强的滤除噪声能力，同时还能够较好地保持图像的细节纹理特征、改善图像质量、提高信噪比等。

2 商空间粒度理论

商空间粒度理论是由张钹、张铃教授根据人类处理问题的特点提出的问题求解理论，该理论用(X,f,T)三元组表示一个复杂的实际问题，其中X表示该问题的论域，f(·)表示该论域的属性，用函数f:X→Y表示，其中Y可以是任意集合，也可以是更一般的空间，f(·)可以是单值也可以是多值的；T为论域结构，指论域X中各元素间的相互关系。该理论自提出以来在图像分割[10]、聚类分析[11]、图像检索[12]等方面得到了广泛的应用并取得了较好的效果。

问题求解的商空间理论本质上是一种在集合论的框架下粒度计算模型，从不同的粒度世界研究问题(X,f,T)，就是在不同的等价关系R下对其商空间([X],[f],[T])的研究。然而对于复杂的问题在具体求解时，为了有效降低计算量，一般是从粗粒度空间到细粒度空间选择适当的粒度进行求解，然后再研究不同粒度间的关系、粒度的合成、综合、分解和在商空间中的推理，这主要是基于以下两个原理：

保假原理：若一个命题在粗粒度空间为假，则该命题在细粒度空间中也为假。

保真原理：若一个命题在两个粗粒度空间为真，则在一定条件下在其合成的商空间中的命题也为真。

3 基于商空间粒计算噪声检测与标记算法

3.1 噪声检测的商空间描述

设(X,f,T)表示待检测噪声图像。X为全体像素点组成的论域，f为论域X中像素点的属性函数（如像素值），T为X中像素之间的结构关系（如X中某点的一个八邻域），则([X],[f],[T])就可以描述为不同商空间粒度下的噪声检测窗口。此时噪声的检测过程就是从粗粒度(X,f,T)到细粒度([X],[f],[T])间的变换。

3.2 粒度噪声判别函数的构造

设噪声图像(X,f,T)，I(x,y)为论域X中像素(x,y)点的像素值，X(1)和X(end)分别为X中像素值的最大值和最小值，SI(x,y)表示与(x,y)具有相同像素值的集合，q(k)为控制粒度层次参数k的函数，Td控制噪声阈值，则在该粒度下噪声判别函数定义为：f(x)

3.3 粒度空间的划分

粒度空间是实施粒度计算的重要依据，首先将待检测的噪声图像(X,f,T)分割成块，形成原始的粗粒度空间([X],[f],[T])，并在此粒度下对每块实施检测，然后结合保假原理判断是否需要再划分到细粒度空间中进行判断，直至划分到所能够判断的最细粒度。

3.4 粒度噪声检测

3.5 算法复杂度分析

图1 噪声图片及各种算法结果

图2 噪声图片及各种算法结果

图3 噪声图片及各种算法结果

4 粒度逆谐波均值滤波器（GIHMF）的构造

由逆谐波均值滤波器[13]的除噪特点知，当噪声点为下限噪声时选择Q为负值，当噪声点为上限噪声时选择Q为正值均可达到相应的最佳滤波效果。本文采用的是将商空间粒度理论与逆谐波均值滤波器的优点相结合构造而成的粒度逆谐波均值滤波器。首先对已判断为噪声的点进行分类标记，然后在相应的粒度层次下对图像（即论域X）中灰度值为I(x,y)的噪声点(x,y)进行噪声滤除，得到滤波结果(x,y)，从而达到了较好的滤波效果，有效地提高了运算效率。其中逆谐波均值滤波器表达式如下：

5 实验结果与分析

为了验证本文算法的有效性，本文采用不同算法对不同类型和不同强度噪声图像进行了对比实验。这里给出了部分实验结果。图1（a）是对“lena”增加强度0.4的脉冲噪声而形成的噪声图像，（b）～（e）依次为二维中值滤波（MF2）算法、自适应中值滤波（AMF）算法、K-SVDF算法和本文算法（GIHMF）的滤波结果；图2（a）和图3（a）分别是叶面和蚂蚁的高强度噪声图像，（b）～（e）依次为MF2算法、AMF算法、K-SVDF算法和本文算法（GIHMF）的滤波结果。为了进一步客观评价GIHMF的性能，本文还采用了归正均方差（NMSE）和峰值信噪比（PSNR）作为评价标准进行比较。表1和表2是通过对“lena”增加不同强度噪声得到的NMSE和PSNR。其中归正均方差（NMSE）和峰值信噪比（PSNR）计算公式如下：

其中I(x,y)和(x,y)分别为原图像和滤波后图像在位置为(x,y)的像素值。

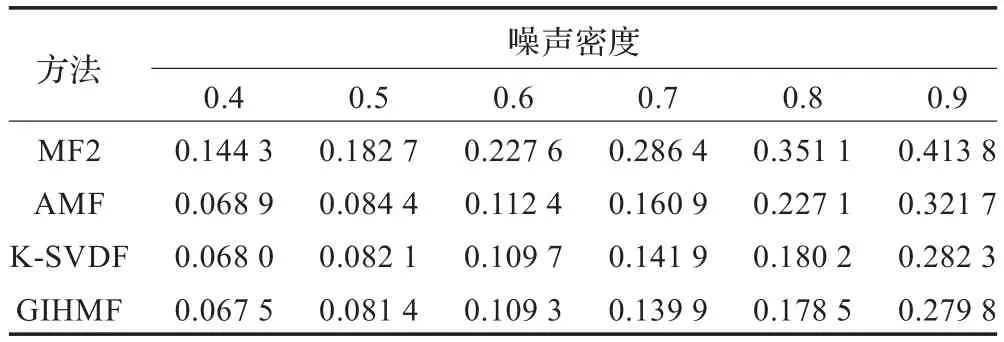
表1 各种方法的归正均方差（NMSE）比较

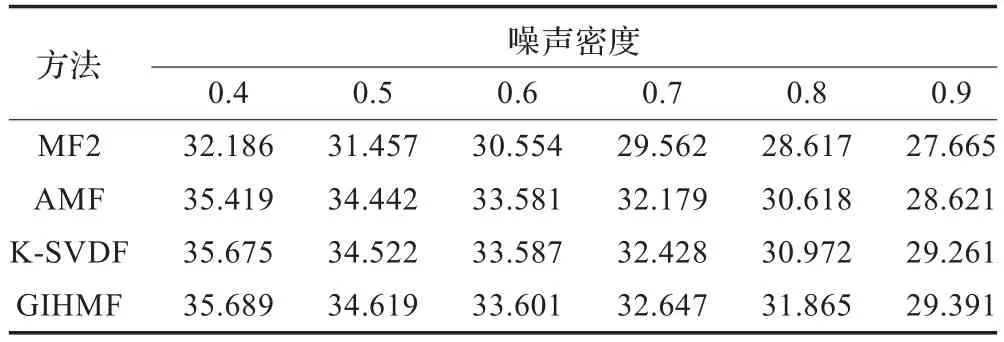
表2 各种方法的峰值信噪比（PSNR）比较

从图1～图3、表1、表2的实验数据可以看出，本文算法在不同噪声强度较MF2和AMF均具有较强的滤波能力（噪声点被滤除得较为彻底或者残留较少），尤其是在噪声污染严重时（图2（a）和图3（a）），在滤除噪声的同时还能很好地保护图像的边缘、纹理、平滑性等细节特征（如图2（d）中叶面的粗细脉络清晰可见且噪声点都被滤除干净，图3（d）中蚂蚁的外形、眼睛和腿都可分辨出来）。同时由表1和表2也进一步说明本文算法的有效性。从表3中的算法滤波效率来看，由于MF2算法只与图像大小有关，故而时间较为固定，但滤波性能最差；而对于自适应中值滤波算法在噪声较弱时，速度较本文算法快，但随着噪声的增强，为了达到较好的滤波效果，增加了滤波窗口增大的次数，降低了滤波效率；而K-SVDF算法的滤波速度始终低于本文算法。

表3 各种方法的滤波速度比较s

6 结论与展望

由于传统的滤波方法在噪声检测中存在的不足使得部分像素点被误检、漏检或运算量较大，同时高低噪声被采用同一种方式进行滤除，致使图像的滤波效果不佳或平滑性遭破坏。本文采用的粒度噪声滤波器和粒度逆谐波均值滤波器，通过选择适当粒度层次进行检测、滤波，避免了噪声间的相互影响，从而改善了滤波效果，保护图像纹理细节特征，改善图像质量，提高信噪比。对于商空间粒度理论在图像处理中的更广阔的应用，还有待进一步的深入研究。

[1]Coyle E J，Gabbouj M，Lin J H.From median filters to optimal stack filtering[C]//IEEE Internet Symp Circuits Systems，1991：9-12.

[2]梁雯，刘松林.图像中心加权中值滤波的改进与应用[J].中国图象图形学报，1997，2（8）：629-633.

[3]Kosj，Lee Y H.Center weighted median filter and their application to image enhancement[J].IEEE Transc Irc Syst，1991，38.

[4]袁世强，谭永红.基于上下中值型噪声检测的自适应中值滤波器[J].中国图象图形学报，2007，12（11）：1971-1975.

[5]于菊珍.一种基于PCNN的图像噪声消去方法[J].信息技术，2008，32（7）：112-114.

[6]Wang Hongmei，Li Bo，Li Yanjun，et al.A new image filtering algorithm for impulse noise[J].Fire Control&Command Control，2011，36（4）：37-39.

[7]Aharon M，Elad M，Bruckstein A.K-SVD：an algorithm for designing overcomplete dictionaries for space representation[J]. IEEE Transactions on Signal Processing，2006，54（11）：4311-4322.

[8]张晓阳，柴毅，李华峰.基于K-SVD和残差比的低信噪比图像稀疏表示去噪算法[J].光学技术，2012，38（1）：23-29.

[9]张铃，张钹.问题求解理论与应用[M].2版.北京：清华大学出版社，2007.

[10]刘仁金，黄贤武.图像分割的商空间粒度原理[J].计算机学报，2005，28（10）：1680-1685.

[11]唐旭请，朱平，程家兴.基于模糊商空间的聚类分析方法[J].软件学报，2008，19（4）：861-868.

[12]许相莉，张利彪，于哲舟，等.基于商空间粒度计算的图像检索[J].计算机研究与发展，2009，46（Suppl.）：337-342.

[13]Gonzalez R C，Woods R E.数字图像处理[M].阮秋琦，阮宇智，译.2版.北京：电子工业出版社，2003.

GAO Zhenglong1,WU Tao1，2,CHEN Xiaobo1,YANG Yingying1

1.School of Mathematical Sciences,Anhui University,Hefei 230601,China
2.Key Laboratory of Intelligent Computing&Signal Processing of Ministry of Education,School of Mathematical Sciences,Anhui University,Hefei 230601,China

For the shortcomings of the traditional filter in the noise detection and filtering,this paper presents a new noise detection method and inverse harmonic mean filtering algorithm based on quotient space granular computing theory.The image with noise is divided into hierarchical granularity to form a semi order quotient space lattice,and then according to principle of falsity preserving,the proper granularity space is selected to classify the noise into two classes and it is filtered respectively.The experimental results show that the algorithm can filter out the noise better while keeping the details of the image texture features,improving image quality,and increasing signal to noise ratio.

quotient space theory;granularity;noise detection;granular-inverse harmonic mean filter

针对传统滤波器在噪声检测和滤除中存在的不足，提出了基于商空间粒度理论的噪声检测和粒度逆谐波均值滤波算法。该算法将受噪声污染的图像划分成不同粒度层次的商空间，形成商空间半序格，结合保假原理选择适当的粒度空间实施噪声分类检测和分别滤除。实验结果表明，该算法在滤除噪声的同时能够较好地保持图像的细节纹理特征、改善图像质量、提高信噪比等。

商空间理论；粒度；噪声检测；粒度逆谐波均值滤波

A

TP391

10.3778/j.issn.1002-8331.1202-0359

GAO Zhenglong,WU Tao,CHEN Xiaobo,et al.Image filtering algorithm based on granular computing theory of quotient space.Computer Engineering and Applications,2013,49（24）：182-185.

国家重点基础研究发展规划（973）（No.2007BC311003）；国家自然科学基金（No.61073117）；安徽大学创新团队（No.KJTD001B）；安徽大学研究生学术创新项目（No.yfc090008）。

高正龙（1985—），男，硕士研究生，主要研究方向：数字图像处理，模式识别；吴涛（1970—），男，教授，研究生导师，主要研究方向：人工神经网络，智能计算，数据挖掘等；陈小波（1985—），男，硕士研究生，主要研究方向：数据挖掘，商空间粒计算等；杨莹莹（1984—），女，硕士研究生，主要研究方向：破产概率的尾分布等。E-mail：gaozl011204@126.com

2012-02-20

2012-06-04

1002-8331（2013）24-0182-04