基于快速分数阶傅氏变换的DDoS攻击检测

陈世文，郭通，黄万伟

国家数字交换系统工程技术研究中心，郑州 450002

基于快速分数阶傅氏变换的DDoS攻击检测

陈世文，郭通，黄万伟

国家数字交换系统工程技术研究中心，郑州 450002

1 引言

分布式拒绝服务攻击（DDoS）[1]利用网络协议和操作系统的漏洞，向攻击目标发送大量服务请求，占用网络带宽资源和主机资源，是影响互联网运行安全最主要的威胁之一[2]。DDoS攻击具有易于发起、并发程度高、隐蔽性强等特点，给传统的基于特征匹配的检测与应对手段带来很大困难。因此，如何准确有效地检测DDoS攻击是一个需要深入研究的问题。

由于DDoS攻击报文本身并不携带任何恶意代码，在内容上完全合法，很难提取到DDoS攻击固有的“指纹”，因此，典型的特征匹配等误用检测方法对于DDoS攻击漏报率高，不能很好地发挥作用，故通常采用基于异常的检测方法，通过比较待测特征与正常模型的偏离程度来识别DDoS攻击。基于异常的检测方法主要包括基于分布特性的检测、基于流量统计异常的检测等方法。

基于分布特性的检测方法利用DDoS攻击存在的分布特性，如源IP地址趋于分散、目标IP地址相对集中等，已提出了监控源IP地址、源目的IP地址对、流连接密度FCD、流特征分布熵TFDE[3-6]等多种方法，这些方法针对性强、检测精度较高，但特征提取与预处理过程复杂，普适性不强，在检测算法上通常还需要采用决策树、支持向量机等机器学习方法，实现复杂度高。基于流量统计异常的检测方法利用攻击时流量的突发性增长特性，Blazek[7]通过监控网络流量与正常流量的偏移来识别攻击，方法简单但精度不高，无法区分正常的大流量和攻击流量，因而误报率较高。

研究表明，网络流量具有自相似性和长相关性[8-9]，而DDoS攻击会影响网络流量的自相似性，使表征网络流量突发特性的Hurst指数产生明显变化。通常，网络流量的Hurst指数在0.5～1之间，Hurst指数越大说明网络的自相似程度越高，突发性也越强，当DDoS攻击发生时，攻击数据包将降低网络的自相似性，引起Hurst指数降低，完全阻塞时流量将趋向于泊松分布过程，Hurst指数变为0.5[10]，已有的Hurst指数估计方法包括方差-时间（V-T）法、R/S（Rescaled Range）法、周期图法、Whittle估计法和小波分析法等[11]。其中，以小波分析法精度高，速度快，但实现过程繁琐，复杂度高。

近年来，分数阶傅里叶变换（Fractional Fourier Transform，FrFT）[12]以其具有的时频旋转特性在信号处理和通信技术等领域得到了广泛的应用[13-16]，Chen等[14]基于FrFT对网络的自相似性进行了分析，并引入局部分析的方法进行Hurst指数估计，估计精度高，但该方法的计算复杂度为O(N2)，无法用于实际流量的Hurst指数求解。针对以上问题，本文提出了一种基于快速分数阶傅里叶变换（FFrFT）求解Hurst指数的DDoS攻击检测方法，通过监测Hurst指数变化阈值判断是否存在DDoS攻击。在DARPA2000数据集和不同强度TFN2K攻击流量数据集上进行了DDoS攻击检测实验，实验结果表明，基于FFrFT的DDoS攻击检测方法有效，相比于常用的小波方法，该方法的计算复杂度低，实现简单且精度更高，能够检测强度较弱的DDoS攻击，有效降低漏报、误报率。

2 基于FFrFT的DDoS攻击检测方法

2.1 FFrFT的定义

分数阶Fourier变换是对经典Fourier变换的推广，分数阶Fourier域可以理解为一种统一的时频变换域[12]。

定义1信号x(t)的a阶分数阶Fourier变换定义为：

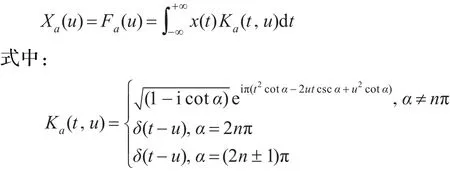
n∈ℤ，α=aπ/2，a为分数阶Fourier变换的阶数，当a=1时，FrFT即为标准Fourier变换。FrFT简记为Fa。

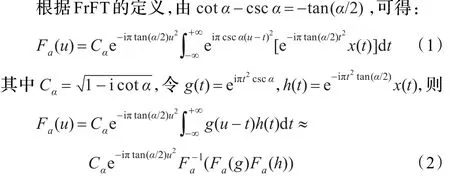
其中(Fa(g)Fa(h))表示位向量乘法，式（2）FrFT的实现需要两次快速Fourier变换和一次FFT逆运算，其计算复杂度为O(NlbN)[13，16]。

2.2 Hurst指数估计

由文献[14]可知，连续小波变换有：

式（3）建立FFrFT与小波变换之间的联系。

通过采用Mallat算法[17]，可得：

由式（3）和式（4），可以得到FFrFT能量谱E[g2(j)]的对数尺度关系为：

为排除采样噪声、序列中的周期成份等因素对Hurst指数估计准确性的影响，采用确定的分形高斯噪声序列（FGN），对比V-T、R/S、小波、FrFT LASS[14]和FFrFT五种方法进行Hurst指数估计的准确性，结果如表1所示。

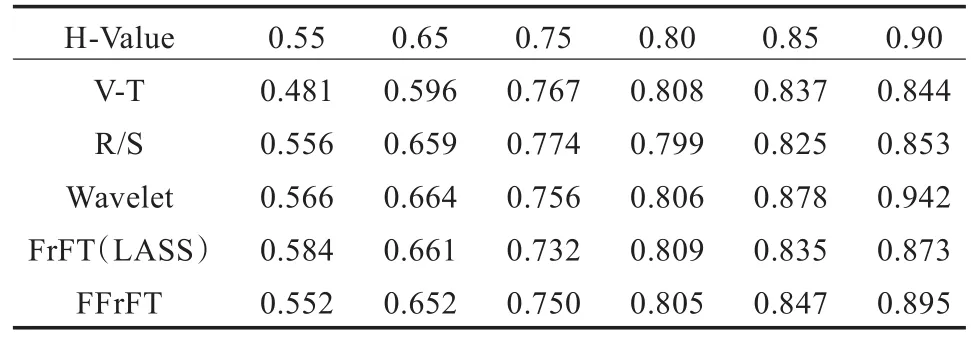
表1 不同方法对FGN序列的Hurst指数估计结果

由表1可知，FFrFT方法的Hurst指数估计精度优于小波等其他方法。同时，V-T、R/S、小波、FrFT LASS[14]和FFrFT五种方法的计算复杂度分别为O(N)、O(N2)、O(NlbN)、O(N2)和O(NlbN)，可知FFrFT方法计算复杂度较低，而且实现简单。因此，综合考虑估计精度、实现复杂度与效率，FFrFT方法优于小波等其他Hurst指数估计方法。

2.3 DDoS攻击检测方法

基于FFrFT的DDoS攻击检测系统框图如图1所示。

在训练阶段，系统对离线数据进行特征提取，即提取每个数据包的到达时间与数据包大小，然后进行数据预处理，按照不同的时间尺度对给定时间间隔内的数据包大小完成统计合并，并利用FFrFT求解Hurst指数，分别采用正常流量与攻击流量数据进行训练，得到Hurst指数的变化阈值，取变化阈值的中心点作为DDoS攻击的判决门限。

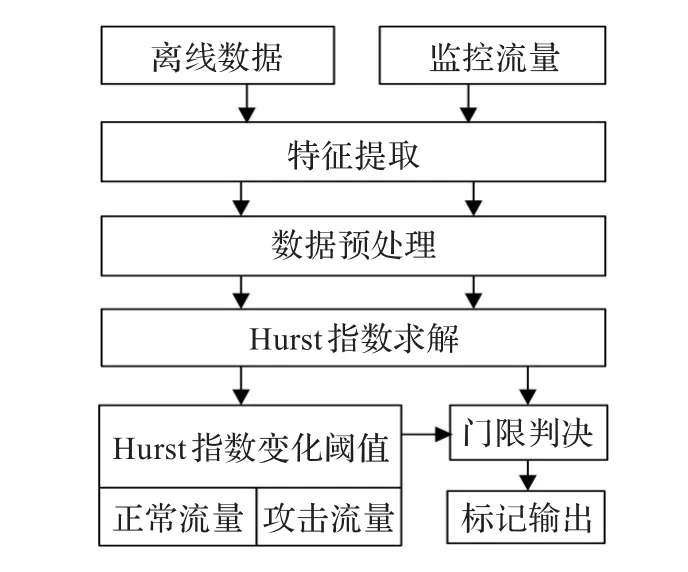
图1 Hurst指数估计DDoS攻击检测系统框图

在检测阶段，对被监控流量进行特征提取、数据预处理并计算Hurst指数，与通过训练设定的判决门限相比较，当Hurst指数下降超过设置门限阈值时，判定发生了DDoS攻击。

采用FFrFT估计Hurst指数的具体算法流程如下：

输入参数：原始数据X[n]，分数阶Fourier变换阶数a，Hurst指数门限θ。

步骤1利用FFT实现原始数据的快速分数阶Fourier变换。

步骤2计算实现FrFT后原始数据的能量谱E[g2(j)]。

步骤3根据G(j)与能量谱的对数关系获得G(j)。

步骤4对不同的尺度区间进行方差拟合度检验，得到最优的尺度区间[j1,j2]。

步骤5根据最优尺度区间进行参数估计。

步骤6利用公式（6）计算Hurst指数估计值。

步骤7计算Δh=Hn-Ha，如果|Δh|＞θ，判断DDoS攻击。

3 实验结果分析

3.1 实验数据集

采用MAWI数据集[18]中的一部分数据作为正常背景流量（2011/10/14），记为Dataset1，MIT Lincoln实验室LLS_ DDoS2.0.2[19]数据集作为攻击数据，记为Dataset2。Dataset2随时间变化的流量如图2所示。

3.2 DDoS攻击检测

从Dataset1和Dataset2中分别提取100 s数据进行混合，其中从Dataset2的236 753个数据包中提取的内容包含攻击数据段。利用FFrFT算法求解Hurst指数，实验结果如图3所示。

由图3可知，正常流量下的Hurst指数基本稳定，发生DDoS攻击时，FFrFT测得的Hurst指数急剧降低，设定Hurst指数变化门限θ=0.25，可以检测到在25～33 s时间段内发生了DDoS攻击。

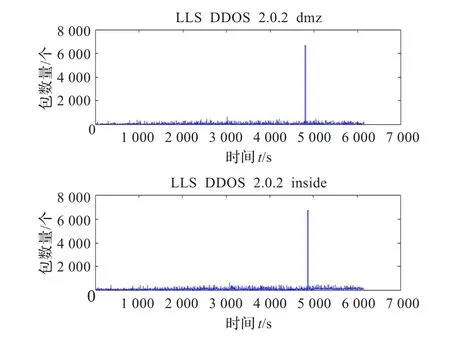
图2 DARPA2000数据集LLS_DDoS2.0.2流量

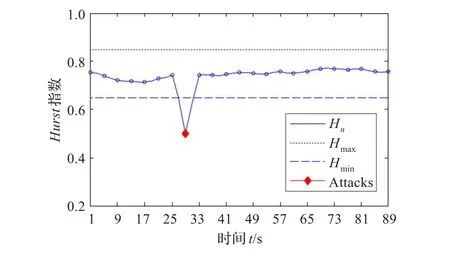
图3 DDoS攻击流量数据的Hurst指数估计

3.3 检测性能对比

采用DDoS攻击工具TFN2K每隔10 s针对攻击目标产生不同强度的攻击数据，并用WinDump捕获后与Dataset1进行混合，在95 s时间内形成9次攻击，采用FFrFT方法和小波方法对其进行DDoS攻击检测，实验结果分别如图4（a）和图4（b）所示。

图4 TFN2K不同强度DDoS攻击的检测结果对比

图4（a）采用FFrFT求解Hurst指数共检测到了9次DDoS攻击，而图4（b）采用小波求解Hurst指数只检测到了8次DDoS攻击，在50 s时强度较弱的DDoS攻击未被发现。比较图4（a）和图4（b）可见，FFrFT方法的攻击检测精度优于小波方法。

4 结束语

本文提出了一种新的利用网络流量自相似性变化检测DDoS攻击的方法，该方法利用快速分数阶Fourier变换求解Hurst指数，通过监测Hurst指数变化阈值判断是否存在DDoS攻击。在DARPA2000数据集和不同强度TFN2K攻击流量数据集上进行了DDoS攻击检测实验，实验结果表明，基于FFrFT的DDoS攻击检测方法有效，相比于常用的小波方法，该方法的计算复杂度低、Hurst指数估计精度更高，能够检测强度较弱的DDoS攻击。因此，基于FFrFT的DDoS攻击检测方法可有效降低漏报、误报率。下一步的研究将考虑如何与机器学习算法相结合，以实现对实时网络流量DDoS攻击的高效检测。

[1]Hakem B，Geert D.Analyzing well-known countermeasures against distributed denial of service attacks[J].Computer Communications，2012，35（11）：1312-1332.

[2]国家计算机网络应急技术处理协调中心.2012年我国互联网网络安全态势综述[EB/OL].[2013-03-20].http：//www.cert.org. cn/publish/main/upload/File/201303212012CNCERTreport.pdf.

[3]Peng T，Leckie C，Ramamohanarao K.Proactively detecting distributed denial of service attacks using source ip address monitoring[C]//Proc of the Third International IFIP-TC6 Networking Conference，2004：771-782.

[4]孙知信，李清东.基于源目的IP地址对数据库的防范DDoS攻击策略[J].软件学报，2007，18（10）：2613-2623.

[5]孙庆东，张德运，高鹏.基于时间序列分析的分布式拒绝服务攻击检测[J].计算机学报，2005，28（5）：767-773.

[6]Lakhina A，Crovella M，Diot C.Mining anomalies using traffic feature distributions[C]//Proc of ACM SIGCOMM2005，Philadelphia，Pennsylvania，USA，2005.

[7]Blazek R B，Kim H，Rozovskii B，et al.A novel approach to detection of“denial-of-service”attacks via adaptive sequential and batch sequential change-point detection methods[C]// Proc of IEEE Systems，Man and Cybernetics Information Assurance Workshop，2001.

[8]Gupta H，Ribeiro V J，Mahanti A.A longitudinal study of small-time scaling behavior of Internet traffic[C]//LNCS 6091：Networking 2010，2010：83-95.

[9]Leland W E，Taqqu M S，Willinger W，et al.On the self-similar nature of Ethernet traffic[J].ACM SIGCOMM Computer Communication Review，1993，23（4）：183-193.

[10]任勋益，王汝传，王海艳.基于自相似检测DDoS攻击的小波分析方法[J].通信学报，2006，27（5）：6-11.

[11]Barulescu A，Serban C，Maftel C.Evaluation of Hurst exponent for precipitation time series[J].Latest Trends on Computers，2010，2：590-595.

[12]Almeida L B.The fractional Fourier transform and time-frequency representations[J].IEEE Trans on Signal Processing，1994，42（11）：3084-3091.

[13]Bultheel A，Martinez Sulbaran H E.Computation of the fractional Fourier transform[J].Applied and Computational Harmonic Analysis，2004，16（3）：182-202.

[14]Chen Yangquan，Sun Rongtao，Zhou Anhong.An improved Hurst parameter estimator based on fractional Fourier transform[J].Telecommun System，2010，43：197-206.

[15]Ciflikli C，Gezer A.Self similarity analysis via fractional Fourier transform[J].Simulation Modeling Practice and Theory，2011，19：986-995.

[16]Campos R G，Rico-Melgoza J，Chavez E.A new formulation of the fast fractional Fourier transform[J].SIAM Journal on Scientific Computing，2012，34（2）：1110-1125.

[17]Percival D B，Walden A T.Wavelet methods for time series analysis[D].New York，USA：Cambridge University Press，2006：56-70.

[18]MAWI working group traffic archive[EB/OL].[2010-12-01]. http：//tracer.csl.sony.co.jp/mawi.

[19]MIT Lincoln Laboratory.2000 DARPA intrusion detection evaluation data set[EB/OL].[2010-12-01].http：//www.ll.mit.edu/ mission/communications/cyber/CSTcorpora/ideval/data/2000data. html.

CHEN Shiwen,GUO Tong,HUANG Wanwei

China National Digital Switching System Engineering and Technological R&D Center,Zhengzhou 450002,China

Aiming at the low detecting accuracy,high training complexity and poor adaptability in DDoS attacks detection methods, a new DDoS attack model based on fast fractional Fourier transform is proposed.It utilizes the principle that DDoS attacks would impact the self-similarity of the traffic,then detects DDoS attacks by monitoring the change range of the Hurst parameter.In DARPA2000 dataset and TFN2K attacks traffic under different intensity,this paper compares the new algorithm with wavelet method and etc.The experimental results reveal that the method has lower compute complexity and better detecting accuracy.

distributed denial of service;fast fractional Fourier transform;self-similarity;Hurst parameter

针对传统检测方法存在精度低、训练复杂度高、适应性差的问题，提出了基于快速分数阶Fourier变换估计Hurst指数的DDoS攻击检测方法。利用DDoS攻击对网络流量自相似性的影响，通过监测Hurst指数变化阈值判断是否存在DDoS攻击。在DARPA2000数据集和不同强度TFN2K攻击流量数据集上进行了DDoS攻击检测实验，实验结果表明，基于FFrFT的DDoS攻击检测方法有效，相比于常用的小波方法，该方法计算复杂度低，实现简单，Hurst指数估计精度更高，能够检测强度较弱的DDoS攻击，可有效降低漏报、误报率。

分布式拒绝服务；快速分数阶Fourier变换；自相似性；Hurst指数

A

TP393.0

10.3778/j.issn.1002-8331.1303-0020

CHEN Shiwen,GUO Tong,HUANG Wanwei.DDoS attack detection based on fast fractional Fourier transform.Computer Engineering and Applications,2013,49（24）：4-7.

国家重点基础研究发展规划（973）（No.G2012CB315900）。

陈世文（1974—），男，博士研究生，CCF会员，研究领域为宽带信息网络，机器学习；郭通（1984—），男，博士生，研究领域为宽带信息网络与高速业务管控等；黄万伟（1979—），男，博士，讲师，研究领域为宽带信息网络。E-mail：ndsccsw@126.com

2013-03-04

2013-07-24

1002-8331（2013）24-0004-04

CNKI出版日期：2013-09-26http://www.cnki.net/kcms/detail/11.2127.TP.20130926.1645.013.html