利用互信息确定延迟时间的新算法

何鹏，周德云，黄吉传，2

1.西北工业大学电子信息学院，西安 710129

2.中国人民解放军驻成都飞机工业公司军事代表室，成都 610092

利用互信息确定延迟时间的新算法

何鹏1，周德云1，黄吉传1，2

1.西北工业大学电子信息学院，西安 710129

2.中国人民解放军驻成都飞机工业公司军事代表室，成都 610092

HE Peng,ZHOU Deyun,HUANG Jichuan.New algorithm for determining delay time by mutual information.Computer Engineering and Applications,2013,49（24）：8-10.

基于过程监控数据的故障诊断是保障复杂系统过程安全、避免重大事故的有效手段，复杂系统工作过程都可采集大量的数据，且这些信号通常表现为较强的非平稳性和非线性，使得对其进行故障特征的提取较为困难。传统方法利用所有变量进行诊断，计算时间长且诊断精度低，增加了系统操作和维护的成本[1]。随着非线性动力学研究的不断进步，特别是将混沌时间序列信号的相空间重构理论[2]应用于设备故障诊断领域，可以从单变量的时间序列中获取系统的有效性息，如相关维数[3]、Lyapunov指数[4]等动力学指标，揭示了故障的本质，从全新的角度更深刻地认识了复杂的非线性动力系统的行为[5]。另外人们将相空间重构理论广泛地应用于各种工程领域，如传感观测信息融合压缩方法及其故障诊断[6]、电力负荷预测[7]等，均获得了让人意想不到的卓越效果。

1 相空间重构

Takens[2]提出的相空间重构方法往往作为对非线性时间序列进行分析的第一步。其基本原理为：由于系统任何一个分量的演化都是由与之相互作用的其他分量所决定的，因此采用时间序列中某些固定的延迟时间的数据点作为重构相空间的高维来处理，即X(n)=[x(n),x(n+τ),x(n+2τ),…,x(n+(m-1)τ)]，重构出轨迹可以表征原混沌系统吸引子的动力学特征，与其微分拓扑结构一致。Takens[2]已经证明，对于一个无限长的无噪声时间序列，延迟时间τ的选取是任意的。然而在实际运用中，采样得到的时间序列必然是有限且含有噪声的，此时恰当选取参数m与τ对重构质量有着至关重要的影响。

选择τ的基本思想是使原采样序列和其延迟序列具有某种程度的独立又不完全无关，从而可以将相邻数据点x(n)和x(n+τ)可以作为相空间重构中的独立坐标来处理。τ太小会造成相邻分量之间的信息冗余，计算量剧增；τ太大会使相邻坐标完全独立，无法获取有效的信息来实现相空间重构。

目前确定重构最佳延迟时间τ的方法主要有三种：自相关函数法[8]、平均位移法[9]与互信息法[10]。其中自相关函数法主要选取序列自相关函数Rxx(τ)第一次降至0的值作为最佳延迟，该方法是对数据线性相关性的描述，本质上不适合分析非线性情形；平均位移法属于一种几何方法，取平均位移函数的斜率降至初值的40%的值作为最佳延迟，具有一定的随意性，理论性不强，并且该方法的结果与嵌入维数m的选取有关，与其构成的联合算法[11]需要反复实验，直到结果收敛一致为止，较为繁琐。采用序列互信息函数的第一局部极小值作为最佳延迟的方法，理论基础完善，且可独立于嵌入维数m进行单独选取，较为理想。但在实际运用中由于互信息的计算量大，难以编程实现等特点极大地限制了它的运用。

2 计算序列间的互信息

从信息论[12]的角度出发，采用平均互信息量来计算采样序列与其延迟序列的关联程。在利用系统某一变量的观测值作为时间序列来进行相空间重建的过程中，取得的观测点列为x(i)，i=1,2,…,N′，为分析x(n)和x(n+τ)之间的相关性，选取延迟量x(i+τ)构成新的点列y(i)，通过计算x(i)和y(i)的互信息大小即可获得其相关性，其中τ=n×t，t为采样间隔时间，构成点对总数为N，N=N′-n。

由于随机变量X或Y的发生及两者间的相关性，使其不确定性减少的熵称为互信息，计算表达式如下：

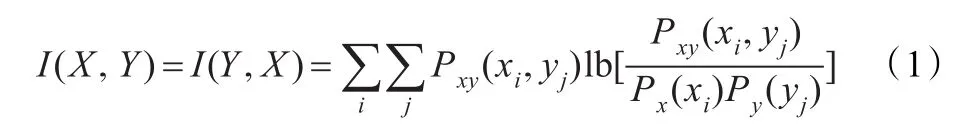
其中，P(xi)为事件xi单独发生的概率，P(yj)为事件yj单独发生的概率，P(xi,yj)为事件xi，yj同时发生的概率。

互信息的计算较为复杂，主要通过对X（横轴），Y（纵轴）的不同划分来进行分类，这里采用Fraser[10]提出的互信息算法，是在边缘分布等概率的基础上划分网格，如图1。

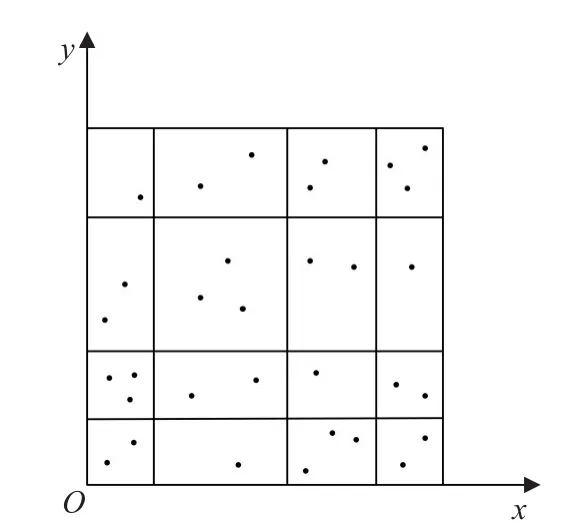
图1 等概率划分网格示意图

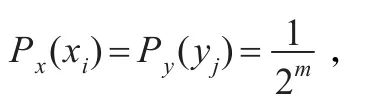
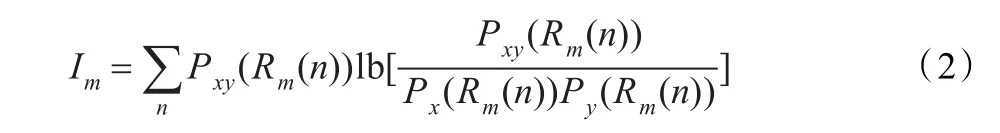
其中，n=1,2,…,Zm，分别对应该层划分的某个网格(xi,yj)，Rm代表进行的是第m层划分。

得到计算系统互信息的递推公式，设

其中网格是否稀疏采用χ2分布的相应准则来判断。根据χ2分布累积分布函数的对照表，χ2分布可以用来测试随机变量之间是否相互独立，也可用来检测统计模型是否符合实际要求。本文可以根据已经设定的网格是否稀疏的阈值，然后对照分布函数的对照表，进一步判断网格是否稀疏，文献[13]中也采取了类似的判断原则。

3 利用互信息确定延迟时间的改进算法

从整体上说，所有现实中的混沌运动系统都是耗散系统[14]，它们在相空间的轨线最终都要收缩到捕捉区中并形成吸引子，具有全局稳定性。但是就局部来说，吸引子内部的运动又是不稳定的，相邻轨道之间相互排斥而按指数形式分离。混沌运动的吸引子是由轨线经过大量的分离和折叠才形成的，把吸引子局部无限放大，可以发现，其内部的结构与形状具有无穷层次的自相似结构，即分形，其运动轨迹具有各态历经性。正是由于混沌吸引子的这些特性，在计算该系统互信息时，往往会出现波峰与波谷交叠的情形，如图2所示。

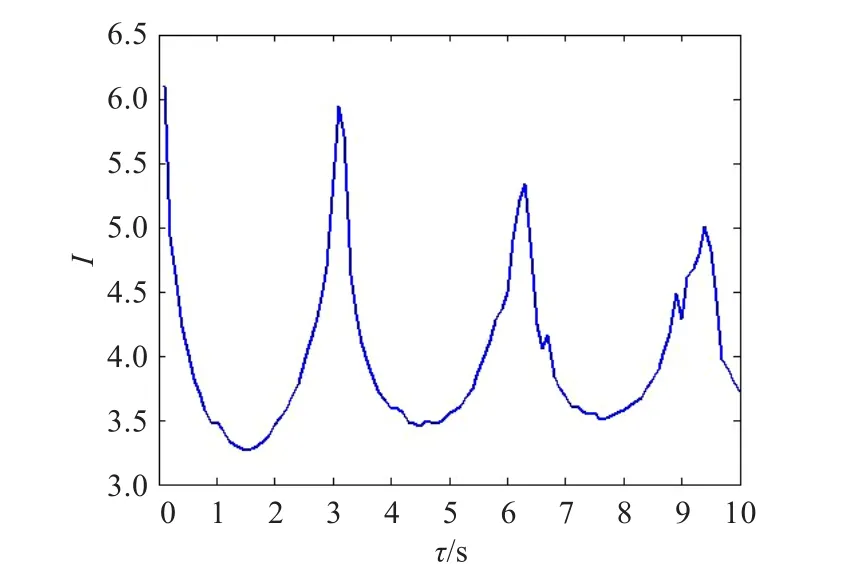
图2 Rössler系统互信息函数

正是由于混沌运动的这种伪周期性，为快速寻找最佳的延迟时间τ提供了便利的条件。提出了一种逐步细化的方法来获得非线性系统互信息的第一局部极小值：首先扩大搜寻的范围，将延迟时间参考值的间隔步长设置得较大，例如若获得的时间序列是对Rössler方程：(a=0.15,b=0.2,c=10)的x分量进行采样，采样间隔时间t=0.1 s，共得到4 096个点，那么首先选择可行的τ值为1 s，2 s，3 s，…，8 s，9 s，10 s，步长为1 s，获得其互信息函数I与τ的关系如图3所示。

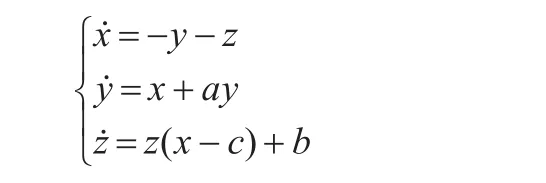
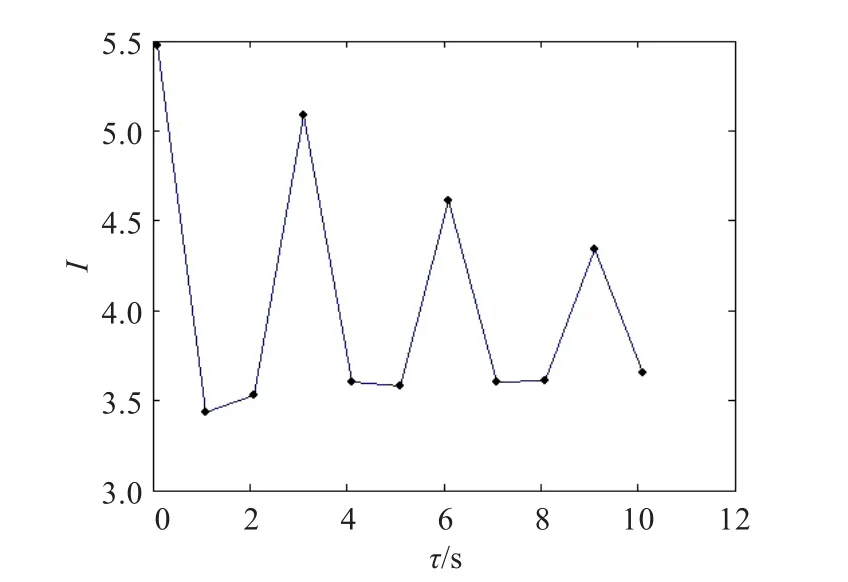
图3 Rössler系统互信息函数(τ=0～1 s)

观察图3可知，第一个极值区间τ为0～0.2 s，下一步将τ的参考值固定在该区间内，步长缩小为0.1 s，获得I与τ的关系如图4所示。

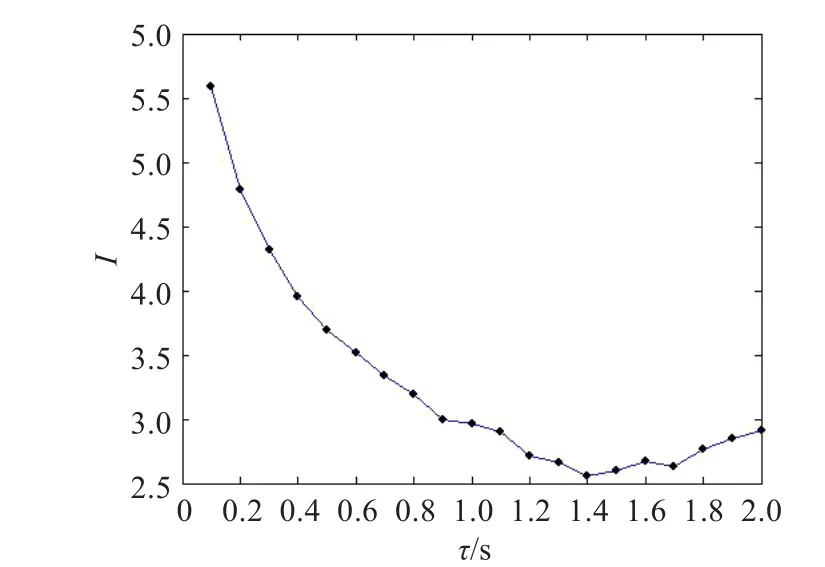
图4 Rössler系统互信息函数(τ=0～0.2 s)

由图4，明显观察得Rössler系统互信息函数的第一局部极小值为τ=1.4，将其作为相空间重构中的延迟时间。为验证提出算法的可行性，将其运用于Lorenz方程：

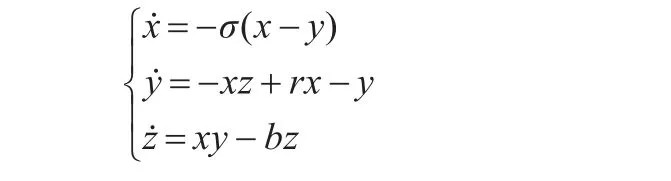
(σ=16,r=45.9,b=4)，采样间隔时间t=0.01 s，t的取值和非线性系统的非线性程度关系较大，对于非线性较弱的系统，一般取值为0.01；对非线性较强的系统，一般取值为0.001；对于未知的非线性系统，通常先取0.01，如果满足要求再增加取值，如果不满足要求，再降低取值。具体步骤如图5所示。

由图5结论，取得Lorenz系统重构的延迟时间τ=0.1 s，与以往的结论一致[15]。

4 算法验证

为验证算法的有效性和可靠性，根据Takens[2]提出的嵌入定理，对Rössler和Lorenz系统选取充分大的嵌入维(m=5)，利用互信息函数的第一局部最小值点所确定的延迟时间进行相空间重构，计算关联维数[3，16]，与理论值进行比较，计算的相对误差均小于5%，证明了该参数选取的合理性。所得结论如表1所示。

5 结论

根据混沌系统本身具有的伪周期性和各态历经性，提出采用逐步细化的方法寻找混沌系统互信息函数的第一局部极小值作为相空间重构中的延迟时间。该方法克服了互信息计算繁琐、耗时较长、难以编程实现等缺点，可以采用递归的方法逐步细化，直到τ的选取步长（即精度）缩小到采样间隔为止，实验结果表明该算法具有较高的可靠性，大大缩短了搜寻时间与计算复杂度，便于推广利用。

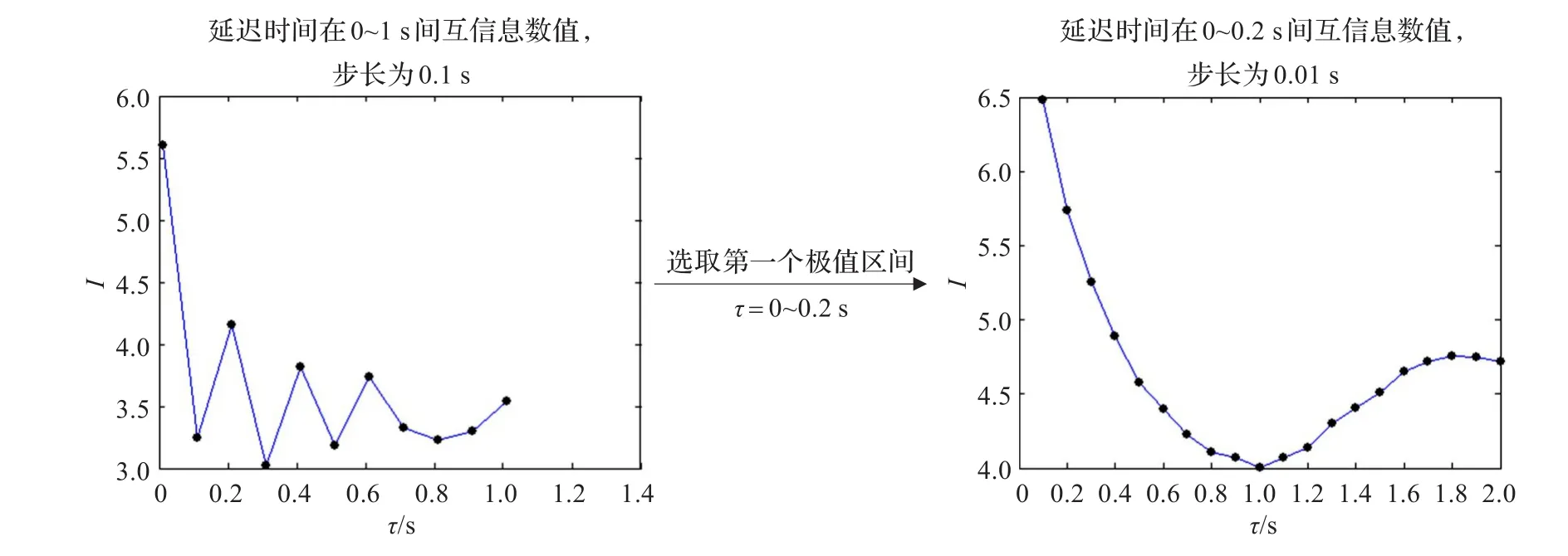
图5 利用互信息确定Lorenz系统延迟时间流程图

表1 关联维数计算结果

[1]刘树林，张嘉钟，徐敏强，等.基于小波包与神经网络的往复压缩机故障诊断方法[J].石油矿场机械，2002，31（5）：1-3.

[2]Takens F.Detecting strange attractors in turbulence[C]//Rand D A，Young L S.Lecture Notes in Mathematics.New York：Springer-Verlag，1981：366-381.

[3]Castro R，Sauer T.Correlation dimension of attractors through interspike intervals[J].Phys Rev E，1997，55：287-290.

[4]Wolf A，Swift J B.Determining Lyapunov exponents from a time series[J].Phys D，1985，16（3）：285-317.

[5]Gans R F.When is cutting chaotic[J].Journal of Sound and Vibration，1995，188（1）：75-83.

[6]钱苏翔，焦卫东，杨世锡.基于独立分量分析的传感观测信息融合压缩方法及其在故障诊断中的应用[J].中国电机工程学报，2006，26（5）：137-142.

[7]李春生，王耀南，陈光辉.基于互信息的组合预测模型及其在电力负荷预测中的应用[J].湖南大学学报：自然科学版，2008，35（9）：58-61.

[8]Albano A M，Muench J，Schwartz C.Singular-value decomposition and the Grassberger-Procaccia algorithm[J].Physical Review A，1988，38（6）：3017-3026.

[9]Rosenstein M T，Collins J J，de Luca C J.Reconstruction expansion as a geometry-based framework for choosing proper delay times[J].Physica D，1994，73：82-98.

[10]Fraser A M，Swinney H L.Independent coordinates for strange attractors from mutual infromation[J].Physical Review A，1986，33（2）：1134-1140.

[11]王海燕，盛昭瀚.混沌时间序列相空间重构参数的选取方法[J].中南大学学报，2000，30（5）：113-117.

[12]周萌清.信息理论基础[M].北京：北京航空航天大学出版社，1993：11-56.

[13]张菁，樊养余，李慧敏，等.相空间重构中延迟时间选取的新算法[J].计算物理，2011，28（3）：469-474.

[14]刘秉正，彭建华.非线性动力学[M].北京：高等教育出版社，2004：143-150.

[15]Martinerie J M，Albano A M.Mutual information，strange attractors，and the optimal estimation of dimension[J].Phys Rev A，1992，45：7058-7064.

[16]Hentschel H G E，Ocaccia I.The infinite number of generalized dimensions of fractals and strange attractors[J].Physica D，1983，8：433-435.

HE Peng1,ZHOU Deyun1,HUANG Jichuan1，2

1.Electronic Information Institute,Northwestern Polytechnical University,Xi’an 710129,China
2.Military Representative Office of PLA Residing in Chengdu Aircraft Industry Corporation,Chengdu 610092,China

This paper analyzes different methods for determining delay time in state space reconstruction.Although the method of mutual information is more accurate,its computational process is quite cumbersome and time-consuming.So based on the pseudo-periodicity of chaotic attractor,it puts forward a new algorithm to refine delay time step by step using mutual information. The numerical experiment of Rössler and Lorenz systems proves the reliability of this algorithm.

state space reconstruction;time series;delay time;mutual information;pseudo-periodicity

对比研究混沌时间序列相空间重构中对延迟时间选取的各种算法，根据混沌吸引子所具有的伪周期性与各态历经的性质，提出采用逐步细化的方法寻找系统互信息函数的第一局部最小值，作为最佳的延迟时间。克服了传统互信息函数计算繁琐、难以编程实现的缺点，兼具精确性与高效性。通过Rössler和Lorenz系统的数值仿真结果验证了算法的可靠性。

相空间重构；时间序列；延迟时间；互信息；伪周期性

A

TP301.6

10.3778/j.issn.1002-8331.1303-0426

航空科学基金（No.20115553021）。

何鹏（1984—），男，博士研究生，研究领域为智能化指挥与控制工程；周德云（1964—），男，博士，教授，研究领域为预测控制、自适应控制、智能控制理论及其应用、复杂系统建模、航空武器系统工程等；黄吉传（1980—），男，博士研究生，工程师，研究领域为现代火力控制理论。E-mail：hp17@163.com

2013-03-27

2013-07-29

1002-8331（2013）24-0008-03

CNKI出版日期：2013-09-26http://www.cnki.net/kcms/detail/11.2127.TP.20130926.1645.011.html