一种改进的放大图像边缘修复算法
于媛媛,王兆仲
北京航空航天大学 图像处理中心,北京 100191
一种改进的放大图像边缘修复算法
于媛媛,王兆仲
北京航空航天大学 图像处理中心,北京 100191
1 引言
图像以矢量图或位图的格式显示在计算机上。对一幅图像进行放大,会在一定程度上造成边缘区域信息的损失。位图由单个的像素点组成,当放大位图时会增大单个像素,从而使线条和形状显得参差不齐,出现模糊和锯齿现象。矢量图使用点、线、矩形等来描述图形。由于这些图形的元素是通过数学公式计算获得,因此矢量图放大不会失真,但是矢量图难以表现色彩层次丰富的逼真图像效果。针对上述存在的问题,提出了一个放大图像边缘修复算法。本文算法既能有效减少放大图像引起的失真,又能保持丰富逼真的图像效果,同时提高了算法运行速度。经研究表明,能否增加图像边缘的光滑度,减弱锯齿现象决定了边缘修复效果的好坏。
从受损区域周边像素获取有效信息,并且选取一定的像素填充方法,即可恢复出放大后图像清晰的边缘。本文算法的两个新颖之处是:(1)对初始放大图像的边缘轮廓进行分段三次Hermite插值,可以生成相对光滑的矢量图像边缘。(2)通过距离变换求取地势图。有了地势图就可以利用分水岭变换求出填充优先权,从而引导后期的填充过程。传统的分水岭算法主要用于图像分割上,这里用于确定像素的填充优先权上[1]。
Inpainting-Based Enhancement[1-2],Anisotropic Diffusion[3-4]和Shock Filters[5-6],Bilateral Filter[7-8]及单帧超分辨率重建是一些具有图像增强和放大功能的算法。但是,这些方法仍然会在一定程度上产生模糊的边缘。Shock Filters起初用于对信号/图像进行去模糊,并且在原始信号拐点处产生冲击信号。这个方法对噪声比较敏感,适用于原本模糊程度较小的图像,否则会产生相反的效果。改进的GSZ shock-filter[5]更适用于灰度图像,处理彩色图像效果并不理想。Anisotropic Diffusion考虑了各向异性的扩散,以保证边缘处的边界连续,但是计算不稳定。Bilateral Filter效果总体很好,边界清晰且光滑,但是在运行效率上有待改进。Inpainting-Based Enhancement同样是基于分水岭的算法,运行时间大大改善,并且能够形成较为清晰的图像边缘,不足之处是对图像梯度较为敏感,并且边缘不够光滑。本文算法是在Inpainting-Based Enhancement的基础上加以改进,使用距离变换解决了对图像梯度敏感的弱点,通过分段三次Hermite插值改善了边界的光滑度。由于只有模糊边缘区域的像素会进行修复,其他像素保持不变,因而避免了块效应的产生。总之,本文算法在理论上确保了边缘像素值的不连续性和边界曲线的光滑度。
2 算法流程
本文算法由以下四个步骤组成:(1)初始放大。本文选用一种简单的方法,即立方卷积插值放大。(2)计算图像地势。对第一步放大后的图像进行距离变换,得出度量任意像素距离图像边界的标准,这里称之为图像地势:距离图像边缘越近的像素所处的地势越高。此处的处理对应于分水岭变换用到的地势函数。同一地势的像素存储到一个队列中,从而进行后面的填充处理。这个操作对算法运行效率的提高起到了至关重要的作用。(3)确定标记图像。这个步骤也就是标记哪些像素是已知像素,哪些像素是未知像素。其中未知像素组成的区域是待修复区域。用分段三次Hermite插值提取出一个更为光滑的图像边缘,再进行一定程度的膨胀处理,即可自动确定待修复区域。(4)像素填充。填充优先权如何确定,对一个修复算法来说是至关重要的,尤其是基于样本的图像修复方法[9]。在新的修复算法中,填充优先权可以描述为:距离图像边界越远的像素点,具有越高的填充优先权。利用分水岭算法中的迭代公式对每一高度进行填充,当填充后的像素在边界处相遇时,整个填充过程就完成了,清晰的边界自然生成。图1为上述过程的流程图。
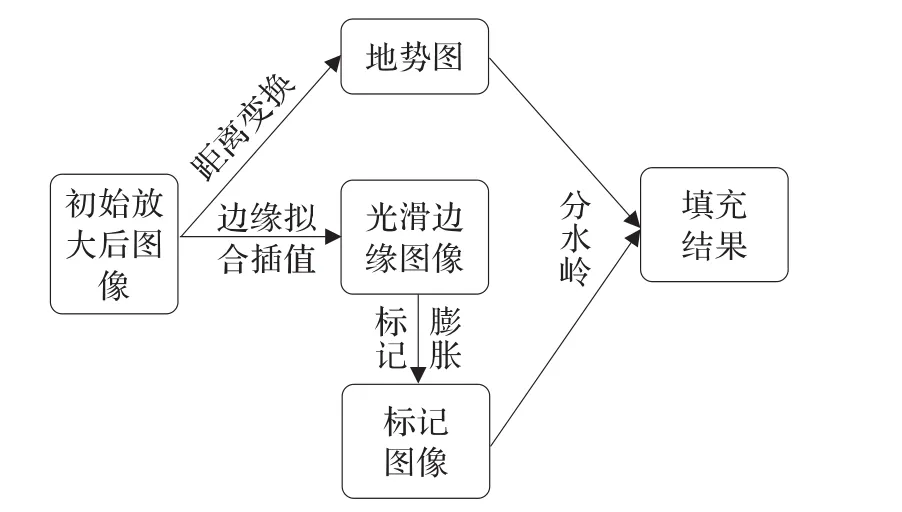
图1 图像边缘修复流程图
3 算法原理
上一章描述了算法的整体框架,并且用流程图表示出来,下面分节描述具体算法原理。
3.1 地势图的确定
距离变换在数字图像处理中应用十分广泛,尤其是应用于骨架提取上。本文则是通过距离变换求取每一像素的地势值,从而得到填充处理所需的地势图。
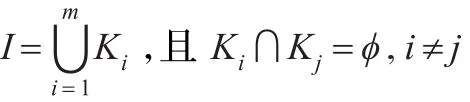

对于二值图像中的每一个像素,距离变换的结果说明了这个像素与图像中最近的非零点的距离[10]。更确切地说,设B={(x,y)|(x,y)∈Kc},欧式距离变换[10]就是对图像I中所有像素点(i,j)求:

不同的距离定义,对应不同的距离变换方法。欧氏距离变换的主要优点是运行速度比较快。在本文算法中,距离变换主要用来衡量图像中任一像素到图像边界的距离:图像边缘处像素地势最高,离边缘处越远的像素地势越低。此处的图像边缘通过Canny边缘检测算子求取。结合到数据结构中队列的知识,同一地势的像素存储到一个队列中,从而进行后面的填充处理。
3.2 标记图像的求取
求出地势图后,就要求取标记图像。最初的标记图像是在Canny边缘检测算子的基础上确定的,继而对边缘进行膨胀操作,获得预定的标记值。针对Canny算子具有本身的针对性和局限性,例如抑制噪声和检测低强度边缘能力不足[11]。本文算法在提取边缘的这一环节采取边缘轮廓拟合插值。为了避免高次插值可能带来的大幅波动现象,实际上通常采用分段低次插值来提高拟合程度,选取分段三次Hermite插值。
在实际插值问题中,为了使插值函数能更好地和原来的函数重合,不但要求二者在节点上函数值相等,而且还要求对应的导数值相等,甚至要求高阶导数也相等。满足这种要求的插值多项式就是Hermite插值多项式。设a≤x0,x1,…,xn≤b为区间[a,b]的一个分割,定义在[a,b]上的分段线性插值函数Ih(x)的导数是间断的,若在节点xk(k=0,1,…,n)上除已知函数值fk外还给出导数值,这样就能构造出一个导数连续的分段三次插值函数[12]Ih(x),满足:(1)Ih(x)∈C[a,b];(2)在每个小区间[xk,xk+1]上是三次多项式。若在整个区间上定义一组分段三次插值基函数αj(x)及βj(x)则Ih(x)可表示为:
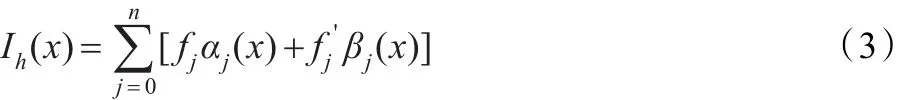
图2为经典lena图像的原始边缘轮廓与分段三次Her-mite插值后的边缘轮廓对比图。其中,(a)图为Canny边缘检测算子确定的原始边缘,(b)图为插值后边缘。由图2可知,分段三次Hermite插值产生的边缘轮廓减弱了原始轮廓的波动性,减少了锯齿现象,生成的边界曲线更为光滑。边缘轮廓的光滑与否决定了填充后图像边缘的光滑程度。因此,分段三次Hermite插值的选取在理论上确保了填充后图像边界曲线的光滑度。


图2(b)分段三次Hermite插值结果对比图
除了分段三次Hermite插值外,还有其他插值方法如三次样条插值[13]。三次样条插值虽然会避免使用高阶多项式出现的龙格现象,但是产生的边缘过于波动,生成的填充图像边缘会出现较多的锯齿。实际计算中,三次样条插值还需要引入边界条件,在运行效率上并不占优势。
插值处理后,在求出的边缘轮廓基础上进行膨胀处理,得到前述的标记图像。本文中规定未知像素的标记值为0,边界区域像素的标记值为255,已知像素标记值则依据距离变换的结果标记为1~254。标记图像的确定为后期像素填充起到了关键的引导作用。
3.3 像素的填充
上述两节分别求出了地势图和标记图像。有了这两个数据,接下来就可以利用分水岭变换进行具体的填充处理。
分水岭的概念可以通过浸没模拟[14]来得到很好的说明。这个概念是以对图像进行三维可视化处理为基础的。传统的分水岭变换与图像的梯度有密切联系。本文利用了距离变换的中间结果克服了对图像梯度敏感的缺点。
I为图像域且I=Θ∪Ω其中Θ代表已知像素的区域,Ω代表待修复区域,即包含模糊边缘的区域。在待修复区域Ω存在一个地势函数g,g可取为对初始放大后图像进行距离变换的结果,即前述的地势图。T[n]是g在高度n上的阈值n为距离变换后对应的高度值。令B[n]为高度n上的汇水盆地[14],有下面的迭代公式:
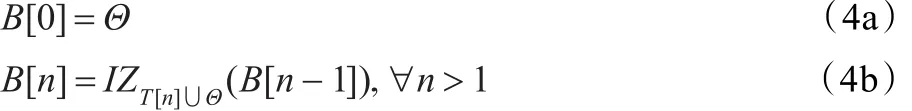
其中,IZ为测地影响区域[1]。随着高度n从1逐步上升,集合B[n]B[n-1]中的元素对应每一高度待修复的像素集合。初始部分B[0]被视为已知区域Θ。B[1]为B[0]的边界上的像素。从B[1]中选出满足g(p)=1的点p。然后再寻找未填充的点q∈IZT[1]∪Θ(B[0])。上述点q就是待填充的点。在填充结束后,再次寻找未填充的点并进行填充,直至所有点都处理完毕。然后令n=n+1来填充更高的地势。
上面的填充过程体现了填充优先权:距离图像边界越远的像素点,具有越高的填充优先权。为了防止求得的图像边缘过于尖锐,可令:

Α为初始放大后图像,α为根据实际选取的0~1的系数。若α=1,则退化为I(q)=I(p),即具有阶梯现象的结果。若α=0,则为初始放大后的图像。
4 实验分析
实验采用Matlab编程实现以上的修复算法,程序运行在CPU E7500@2.93 GHz,2 GB内存的计算机上。选取彩色图像作为原始数据。图3为实验选取的测试图像。图4说明了修复步骤:图4(a)中初始放大使用立方卷积插值放大,放大倍数理论上可选取算法允许的任意整数,本文选取10;图4(b)为距离变换的处理结果,可以清楚地看到任意像素到图像边缘的距离:越靠近边缘点,像素值越高;图4(c)为利用边缘拟合插值(分段三次Hermite插值)并进行膨胀处理后的结果,白色区域为自动确定的待修复区域;图4(d)为填充后的结果,其中将式(5)中的参数α设为0.8。这样设置的原因如图5所示,该图针对同一幅图像选取不同的α求出相对立方卷积放大图的峰值信噪比曲线(PSNR)。由数据可知,α的值越高,PSNR值越高。但当α取1时会产生较严重的阶梯现象。既考虑客观指标,又考虑主观视觉感受。因此参数选取0.8,从而兼顾了主客观指标。

图3 测试图像

图4 数字图修复过程
图6为本文方法与立方卷积插值方法的对比,可以明显地看到边缘轮廓变清晰且光滑。图7为将本文方法与Anisotropic Diffusion(AD),Bilateral Filter(BF)和Inpainting-Based Enhancement(IBE)相对比的结果。从图中看出,本文修复算法有明显的改进效果。AD算法由于考虑到各向异性扩散,保证了边缘处的边界连续,但是边界并不够清晰。BF算法主要原理是对图像进行滤波,但该算法仅考虑了破损区域边缘周围的像素值,导致当放大倍数足够大时效果并不理想。这两个方法都耗费了大量时间。IBE算法边缘界限清晰,但是毛刺过多。采取分段三次Hermite插值的方法,获取更为光滑的边缘线条,从而减少毛刺,减弱锯齿现象,并且在像素填充方法上有所改善,减小了填充误差的概率。综合来看,本文方法与AD和BF相比边缘上更为清晰。与IBE相比,边缘线条更为光滑。表1为将立方卷积插值放大图像作为原始数据,对四种方法求取峰值信噪比的结果。由结果可知,本文方法PSNR比其他方法平均都能高出2 dB,也从客观上证明了本文改进效果。表2为运行时间对比结果。AD和BF效率较低,本文算法比IBE多出几个步骤,因此所需时间增加,但是效率仍然较高。
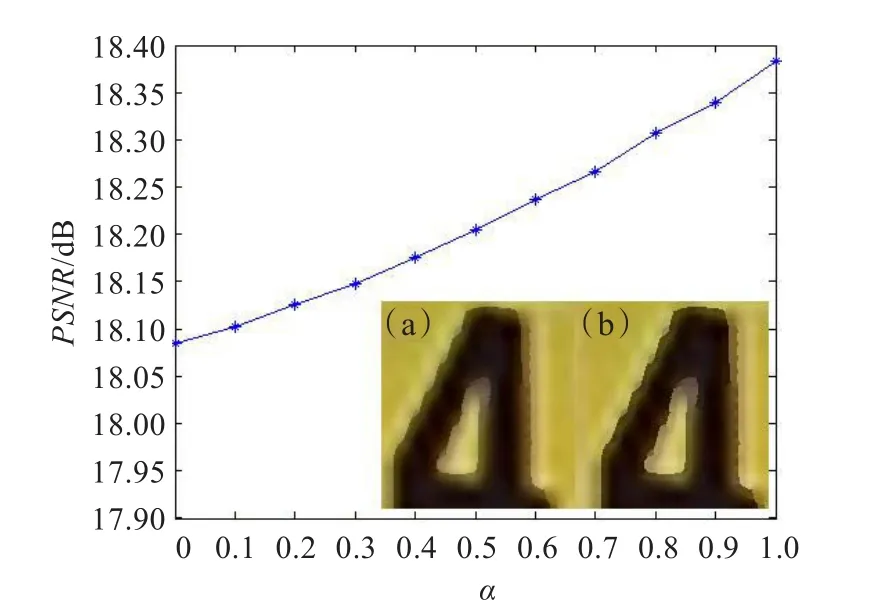
图5 数字图选取不同α的峰值信噪比曲线

图6 人脸图、鹦鹉图立方卷积插值
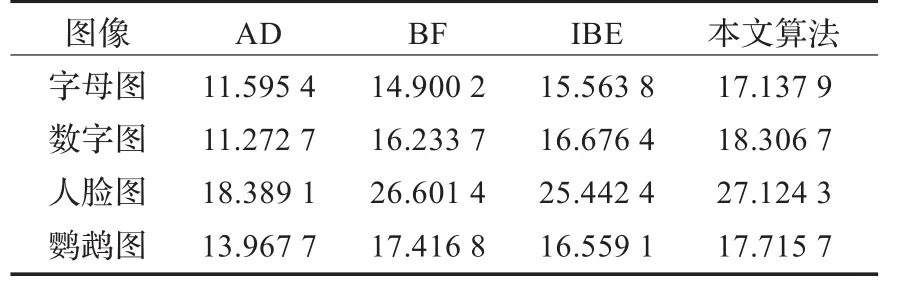
表1 四种方法峰值信噪比dB
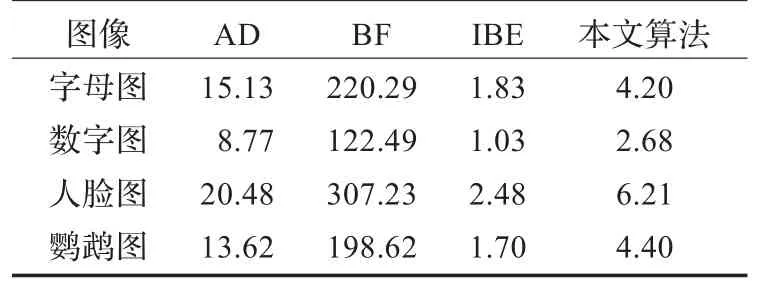
表2 四种方法运行时间s

图7 字母图修复效果对比
5 结论
由于很多插值放大算法并不能同时保证边缘的清晰与光滑,本文针对这个问题,提出了基于边缘轮廓拟合插值和分水岭变换的像素填充方法。由结果可知,本文算法在保持放大图像的清晰且光滑边缘上有明显的效果。并且在理论上保证了边缘区域像素值的不连续性和边界曲线的光滑度。此外,很多插值方法都很耗时,本文由于利用队列存储中间变量,并且只选取边缘区域进行修复,在效率上有明显优势。本文算法也存在着其他不足,例如仍有少量毛刺,这些问题有待进一步改进。
[1]Wang Zhaozhong,Li Y F.Watershed-guided inpainting for image magnification[C]//19th International Conference on Pattern Recognition(ICPR),2008:1-4.
[2]Wang Zhaozhong.Image inpainting-based edge enhancement using the eikonal equation[C]//International Conference on Acoustics,Speech,and Signal Processing(ICASSP),2011.
[3]Τschumperle D,Deriche R.Vector-valued image regularization with PDE’s:a common framework for different applications[J]. IEEE Τransactions on Pattern Analysis and Machine Intelligence,2005,27:506-517.
[4]Weickert J.Anisotropic diffusion in image processing[M].Stuttgart,Germany:Τeubner-Verlag,1998:87-88.
[5]Welk M,Weickert J,Galic I.Τheoretical foundations for spatially discrete 1-D shock filtering[J].Image and Vision Computing,2007,25(4).
[6]Cheriet M,Remaki L.Enhanced and restored signals as a generalized solution for shock filter models[J].Journal of Mathematical Analysis and Applications,2003,279(2).
[7]Paris,Durand.A fast approximation of the bilateral filter using a signal processing approach[J].International Journal of Computer Vision,2009,81(1).
[8]Zhang Ming,Gunturk B K.Multiresolution bilateral filtering for image denoising[J].IEEE Τransactions on Image Processing,2008,17(12).
[9]Criminisi A,Perez P,Τoyama K.Region filling and object removal by exemplar-based image inpainting[J].IEEE Τransactions on Image Processing,2004,13(9):1200-1212.
[10]车武军.距离变换与中轴变换在变形问题中的应用研究[D].杭州:浙江大学,2003.
[11]贺强,晏立.基于LOG和Canny算子的边缘检测算法[J].计算机工程,2011,37(3):210-212.
[12]Vincent L,Soille P.Watersheds in digital spaces:an efficient algorithm based on immersion simulations[J].IEEE Τrans on Pattern Analysis and Machine Intelligence,1991,13(6):583-598.
[13]许小勇,钟太勇.三次样条插值函数的构造与Matlab实现[J].兵工自动化,2006(11):76-78.
[14]冈萨雷斯.数字图像处理[M].北京:电子工业出版社,2005:428-431.
YU Yuanyuan,WANG Zhaozhong
Image Processing Center of Beihang University,Beijing 100191,China
Τo preserve sharp and smooth edges in magnified images,an algorithm based on contour fitting interpolation and watershed transform is proposed.Τhe main idea of the algorithm is to magnificate the original image,and automatically locate blurry edges,and do the inpainting process.Τhe edges of initially magnified image are extracted by piecewise cubic Hermite interpolation.A mark image is automatically obtained through edge expansion.A distance transform is applied on the initially magnified image to provide the relief image for watershed algorithm.With the help of the mark and relief image,pixels in blurry regions are gradually filled based on the watershed transform.Experiments demonstrate that:compared with some existing algorithms, the method reduces the sensitivity to the image gradient and makes the edges sharper and smoother.Besides,it also has high computational efficiency.
image inpainting;image magnification;distance transform;watershed;pixel filling
为了保持放大后图像清晰且光滑的边缘,提出了一个基于边缘轮廓拟合插值和分水岭变换的边缘修复算法。算法的主要思想是对原始图像进行初始放大,自动确定模糊区域,从而进行修复处理。通过分段三次Hermite插值提取初始放大图像的边缘。对边缘进行膨胀进而自动获取标记图像。对初始放大图像进行距离变换,从而提供了分水岭变换所需的地势图。有了标记图像和地势图就可以利用分水岭变换逐步填充模糊区域像素。实验结果表明:与已有算法相比,该算法降低了对图像梯度的敏感程度,图像边缘更为光滑清晰,并且在运行效率上大大提高。
图像修复;图像放大;距离变换;分水岭;像素填充
A
ΤP391.41
10.3778/j.issn.1002-8331.1203-0408
YU Yuanyuan,WANG Zhaozhong.Improved edge inpainting algorithm for image magnification.Computer Engineering and Applications,2013,49(15):167-170.
国家自然科学基金(No.60803071);教育部博士点基金项目(No.200800061067)。
于媛媛(1988—),女,硕士研究生,主要研究方向为图像处理;王兆仲(1975—),男,博士,硕士生导师。E-mail:quanquan@sa.buaa.edu.cn
2012-03-19
2012-05-22
1002-8331(2013)15-0167-04
CNKI出版日期:2012-07-16 http://www.cnki.net/kcms/detail/11.2127.ΤP.20120716.1500.023.html

