包容性检验和SVM相融合的网络流量预测

郑伟勇，冯广丽

河南工程学院 计算机科学与工程系，郑州 451191

包容性检验和SVM相融合的网络流量预测

郑伟勇，冯广丽

河南工程学院 计算机科学与工程系，郑州 451191

1 引言

随着网络规模扩大，网络管理难度日益增加，而流量预测可以了解网络流量的发生趋势，为网络管理人员合理分配网络带宽，防止网络拥塞提供有价值参考意见，因此，网络流量预测准确性已成为网络管理领域中的研究热点问题[1]。

网络流量受到上网随机性、节假日等因素影响，具有一定的周期性、规律性和非平稳性，传统流量预测方法主要有回归分析法、时间序列法、趋势外推法等[2-4]，这些方法基于线性建模，难以准确反映网络流量复杂变化特点，预测误差较大[5]。基于非线性理论的网络流量预测方法主要有隐马尔可夫、神经网络、支持向量机、灰色理论等，它们具有较好的非线性预测能力，网络流量预测效果较好[6-8]。但是对于不同结构的网络流量，它们的预测性能差异较大，难以获得比较稳定的预测结果。近些年，一些学者提出一些基于组合理论的网络流量预测模型，如：姚奇富等提出的灰色理论和马尔可夫链组合网络流量预测方法[9]；李捷等提出的卡尔曼滤波和小波分析组合的流量预测方法[10]，研究结果表明，组合模型较好地克服了单一模型只能反映网络流量变化的片段、部分信息的缺陷，网络流量预测的精度得以提高[11]。相关研究表明，随便增加单一预测模型个数并不一定提高组合模型的预测效果，而且单一模型间可能存在一定的相关性，使组合预测的输入信息重叠，导致预测准确率降低，因此，在进行网络流量组合建模预测前，选择哪些单一模型对网络流量进行组合预测至关重要[12]。包容性检验方法用于判定一个预测模型是否包括或包容了其他预测模型的有关信息，根据包容性检验的结果，筛选出适用于组合预测的各单一预测模型，有学者将其应用于云计算资源组合预测和舰船装备维修费组合预测[13-14]，结果表明，包容性检验可以进一步提高组合模型的预测准确度，因此为网络流量预测提供了一种新的研究思路。

为了提高复杂多变的网络流量预测的准确度，尝试将包容性检验方法引入到网络流量组合预测模型选择中，提出一种基于包容性检验和支持向量机相结合的网络流量预测模型（EΤ-SVM），并通过仿真实验检验模型的有效性。

2 包容性检验原理

设m1、m2分别表示两个不同的网络流量预测模型，t时刻的实际网络流量值为yt，两模型在t时刻的网络流量结果分别为r1，t和r2，t，考虑如下形式的回归方程：

式中，ut为随机扰动；β1、β2为回归系数，且β1+β2=1。

式（1）两边同时减去r1，t，则有：

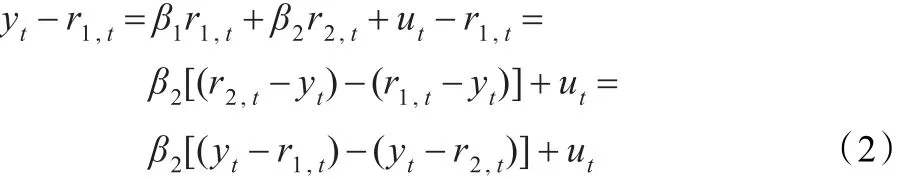
令ei，t=yt-ri，t(i=1，2)，则式（2）就可以转化为：

根据包容性检测原则，则有：

以上是两模型组合的包容性检验原理，但是在实际应用中，一般是两个以上的模型进行组合。对于多个网络流量预测模型，若采用式（1）进行预测模型间的包容性检验，则易出现模型数量过多，无法确定回归系数的问题[15]。

设r1，t，r2，t，…，rk，t分别表示t时刻分别来自k个不同网络流量模型的预测结果，t时刻的实际网络流量值为yt；rc，t为是r1，t，r2，t，…，rk，t网络流量预测模型组合结果；rc(-i)，t表示不包含ri，t网络流量预测结果。

令ec，t=yt-rc，t，ec(-i)，t=yt-rc(-i)，t，在包容性检验中增加截距项，然后根据式（3）得到多模型组合预测的包容性检验为：

检验假设：H0:αi=0，i=1，2，…，k，在αi显著性水平下，通过t统计量检验选择模型。如果t检验显著不为0，则表示ri，t包含原有模型所不具备的信息，组合ri，t，可以提高网络流量的预测效果，ri，t不能被原有模型包容，否则，表示组合ri，t对预测结果没有什么影响，删除ri，t。

3 包容性检测选择网络流量单一模型

（1）采用检测设备对网络流量进行收集，为了提高学习速度，在网络流量数据进行预处理，具体为：

式中，x表示网络流量原始数据，xmin和xmax分别表示最小值和最大值。

（2）采用单一模型对网络流量进行预测，并将预测结果的均方根误差（RMSE）作为模型优劣评价准则，并根据RMSE对模型进行降序排序。

（3）选择预测性能最好的网络流量模型，并根据包容性检验原则，对预测性能最好的模型依次进行检验，看其是否包容其他网络流量模型，若包容了其他网络流量模型，则将该模型从列表中删除，反之，就以一定的组合方式将它们进行预测组合，直到组合模型以外所有其他模型已被删除，那么包容性检验就完成了。

（4）将当前组合模型作为最好模型，继续与其他还没有包容性检验的模型进行检验，不断重复步骤（3）。

（5）将最后所选择单一网络流量预测模型作为最合适的网络流量单一模型。具体如图1所示。

图1 单一网络流预测模型的选择流程

4 SVM的单一模型网络流量预测结果组合

假设通过包容性检验最终选择了m个单一预测模型，对第i个测试样本，m个单一预测模型的预测值分别记为{xi1，xi2，…，xim}，这些值作为自变量，第i个测试样本的实际值作为因变量，对n个训练样本，计算出相应的预测值xij(i=1，2，…，n，j=1，2，…，m)，由此构造n×m个输入向量，它们组成SVM的学习样本，具体如表1所示。

表1 SVM的网络流量学习样本

当网络流量学习样本集为线性时，SVM的回归预测函数可表示为：

式中，w表示权向量，b表示偏置向量。

通过求解一个凸二次规划问题求解式（6）中的w和b，从而得到预测函数。SVM同时考虑经验风险和置信范围，因此可通过最小化下面的目标函数得到问题的解。

式中，第1项使得函数更加平坦从而提高推广能力，第2项是经验误差，常量C称为惩罚系数，体现对样本预测误差的惩罚程度，也是对置信范围和经验风险的一种折衷，Remp(f)为损失函数，本文采用ε不敏感损失函数。

通过引入松弛因子，将式（7）的优化目标函数即转换为：

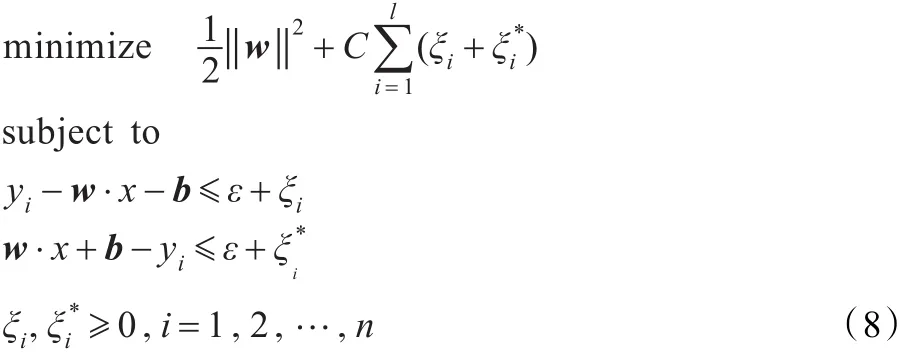
式中，ξi，表示为松弛因子。

为了加快求解速度，通过引入上式的Lagrange函数，并求解下面的对偶形式获得乘子αi，：

在求解实际问题时，网络流量变化具有非线性特点，此时，SVM引入一个映射函数φ将原始数据映射到一个新的特征空间，从而将非线性问题转化为新特征空间中的线性问题，此时，网络流量的SVM回归预测函数可表示为：

式（10）的优化目标函数转化为下面的形式：

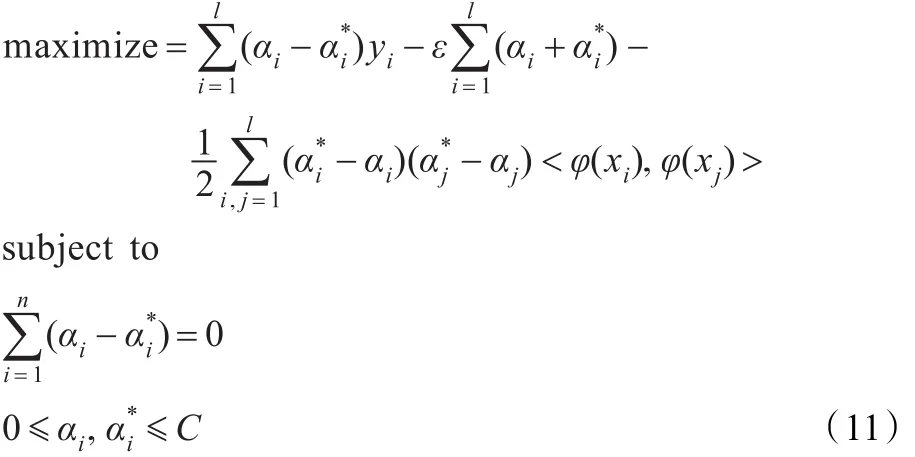
通过引入核函数k(xi，x)代替(φ(xi)，φ(xj))，这样式（11）变为下面的优化目标函数：

5 仿真实验

5.1 数据来源

为了验证EΤ-SVM的网络流量预测模型性能，采用网络流量库：http：//newsfeed.ntcu.net/～news/2011的2011年1月1日到3月11日共100 d每小时访问流量进行仿真实验，共收集到100×24=2 400个网络流量时间序列，具体如图2所示。前2 300个网络流量时间序列组成训练集，建立网络流量EΤ-SVM模型；后100个网络流量时间序列组成测试集，用于检验EΤ-SVM模型的预测性能。

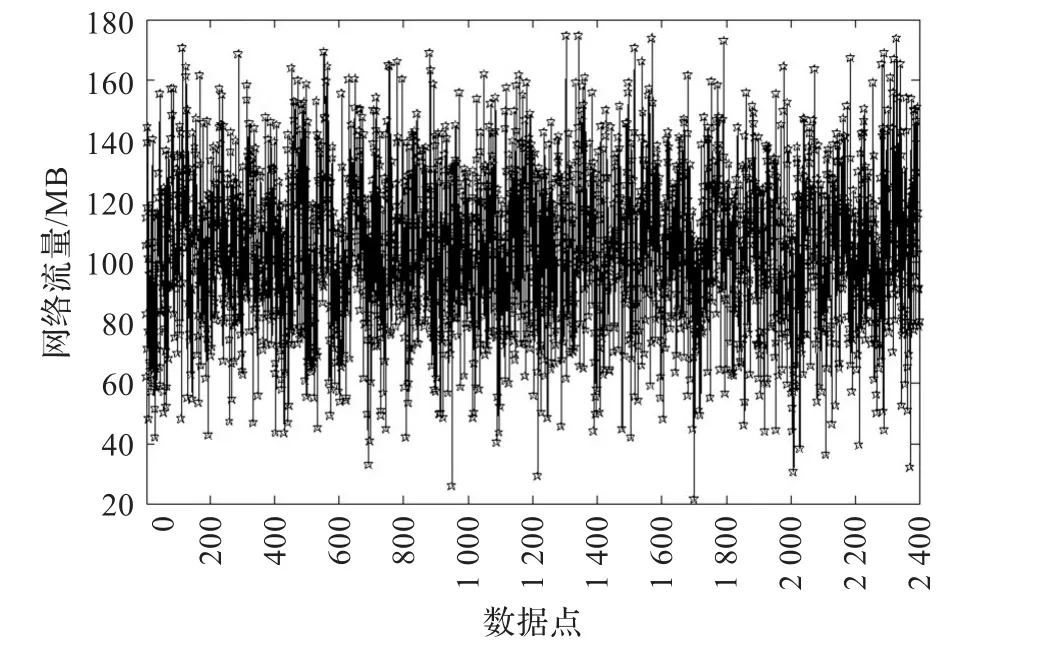
图2 网络流量时间序列

5.2 单一模型预测结果

采用五种单一模型（线性回归分析、趋势外推法、时间序列法、灰色模型和BP神经网络）对网络流量数据进行建模，并对网络流量进行预测，它们的RMSE见表2。

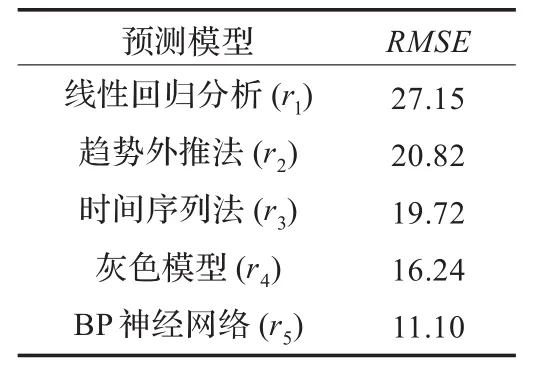
表2 各模型预测结果的RMSE值

5.3 包容性检验选择单一模型

（1）根据表2单一模型预测结果的RMSE对模型进行排序：r5、r4、r3、r2、r1，将这些模型按顺序输入待评表。选择r5为基本模型，将其从待评表移至备选表中。

（2）在a=0.05的显著性水平下，对r5和r4进行包容性检验，得到t统计量为4.155，查t分布临界值表，可以得到t0.0025=2.878，有t=4.006 7＞2.878，根据接受原则，r5和r4不包容，因此采用SVM将r5和r4进行组合，组合模型记为r54。

（3）在a=0.05的显著性水平下，将模型r54对模型r3进行包容性检验，t统计量为3.300，查t分布临界值表，可以得到t0.0025=2.142，有t=3.300＞2.142，根据接受原则，r54和r4不包容，因此采用SVM将r54和r3进行组合，组合模型记为r543。

（4）将r543对r2进行包容性检验，t统计量为 -0.539，查t分布临界值表，可以得到t0.0025=1.763，有|t|=0.539＜1.763，根据接受原则，r543和r2互相包容，因将r2从待评表中删除。

（5）将r543对r1进行包容性检验，t统计量为 -0.115 7，查t分布临界值表可以得到t0.0025=1.562，有|t|=0.115＜1.562，根据接受原则，r543和r2互相包容，因将r2从待评表中删除，此时，待评表已经为空，停止包容性检验。

（6）将组合模型r543作为最终选择的单一预测模型。

5.4 SVM对单一模型预测结果进行组合

采用所选择的时间序列法、灰色模型和BP神经网络分别对网络流量进行预测，得到相应的预测结果，然后将预测结果构成输入向量，实际测试集的网络流量作为期望输出，输入到SVM进行学习建模，最后得到网络流量的预测结果，结果如图3所示。

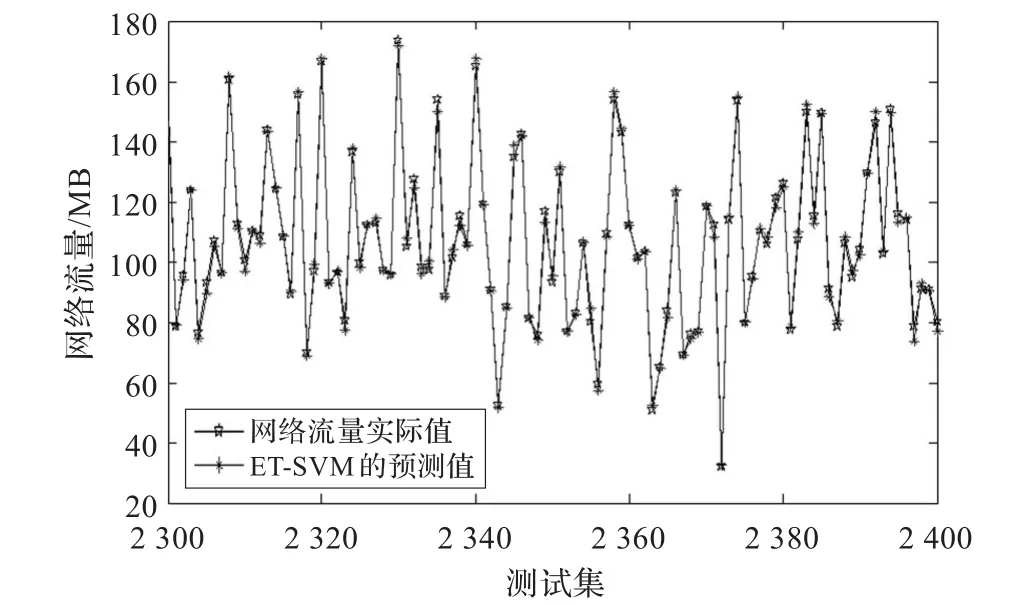
图3 EΤ-SVM的预测结果

5.5 与单一模型预测结果比较

采用时间序列法、灰色模型和BP神经网络对网络流量进行预测，它们的预测结果分别如图4所示。从图3和图4预测结果进行分析可知，EΤ-SVM的预测值与实际网络流量值相当接近，而单一模型的预测值与实际网络流量值间的偏差较大，而且EΤ-SVM的预测结果更加稳定，对比结果表明，EΤ-SVM是一种有效的、预测精度高、结果可靠的网络流量预测方法。

5.6 与单一模型预测误差对比

为了更加全面描述模型的优劣，采用RMSE和平均绝对百分误差（MΑPE）作为模型性能的评价指标，它们定义

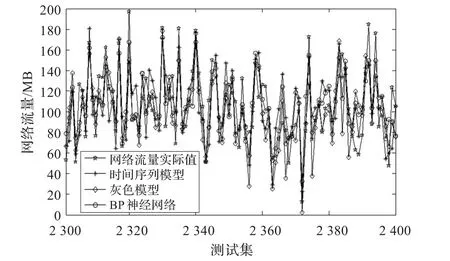
图4 各单一模型预测结果

如下：

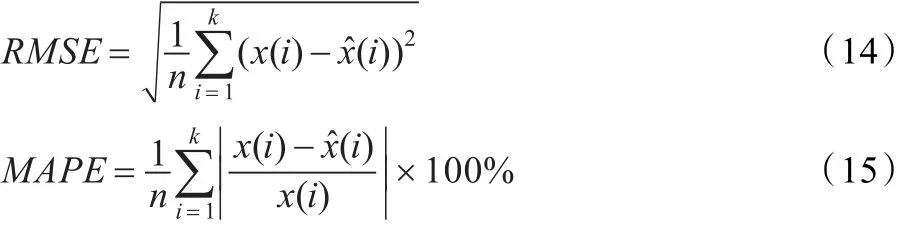
式中，xi和分别为网络流量实际值和预测值，n为测试样本数。

各模型的RMSE和MΑPE见表3。从表3可知，EΤ-SVM预测结果的误差要小于参比模型，网络流量的预测精度得到了提高，对比结果表明，通过包容性检验选择的单一模型可以很好地实现优势互补，对网络流量变化特点进行全面、准确的刻画，建立的网络流量预测模型更好地反映了网络流量变化趋势。

表3 各模型的预测误差对比

6 结束语

针对网络流量组合预测过程的单一模型选择问题，提出一种包容性检验和SVM相融合的网络流量预测模型。仿真结果表明，相对于对比模型，EΤ-SVM提高了网络流量的预测精度，降低了网络流量的平均预测误差，预测结果更加可靠，对复杂多变的网络流量预测具有重要意义。

[1]Nguyen Τ Τ，Armitage G.A survey of techniques for internet traffic classification using machine learning[J].IEEE Communications Surveys and Τutorials，2008，10（4）：56-76.

[2]Silva C G.Τime series forecasting with a nonlinear model and the scatter search meta heuristic[J].Information Sciences，2008，178（16）：3288-3299.

[3]高波，张钦宇，梁永生，等.基于EMD及ARMA的自相似网络流量预测[J].通信学报，2011（4）.

[4]吕林涛，李军怀.时间序列模式及其预测模型算法应用[J].计算机工程，2004，17（4）：3-4.

[5]王俊松，高志伟.基于RBF神经网络的网络流量建模及预测[J].计算机工程与应用，2008，44（13）：6-7.

[6]马华林.基于灰色模型和自适应过滤的网络流量预测[J].计算机工程，2009，35（1）：130-131.

[7]赵振江.基于PSO-BP神经网络的网络流量预测与研究[J].计算机应用与软件，2009，26（1）：218-221.

[8]张颖路.基于遗传算法优化支持向量机的网络流量预测[J].计算机科学，2008，35（5）：177-179.

[9]姚奇富，李翠凤，马华林，等.灰色系统理论和马尔柯夫链相结合的网络流量预测方法[J].浙江大学学报：理学版，2007，34（4）：396-400.

[10]魏永涛，汪晋宽，王翠荣，等.基于小波变换与组合模型的网络流量预测算法[J].东北大学学报：自然科学版，2011，32（10）.

[11]李捷，刘瑞新，刘先省，等.一种基于混合模型的实时网络流量预测算法[J].计算机研究与发展，2006，43（5）：806-812.

[12]汪同三，张涛.组合预测——理论、方法及应用[M].北京：社会科学文献出版社，2008：183-189.

[13]谢力，魏汝祥，訾书宇，等.基于包容性检验的舰船装备维修费组合预测[J].系统工程与电子技术，2010，32（12）：2599-2602.

[14]李洪安，康宝生，张婧，等.基于改进的包容性检验的云计算资源组合预测[J].计算机应用研究，2013，30（1）：252-255.

[15]Fang Y.Forecasting combination and encompassing tests[J]. International Journal of Forecasting，2003，19（1）：87-94.

ZHENG Weiyong,FENG Guangli

Department of Computer Science and Engineering,Henan Institute of Engineering,Zhengzhou 451191,China

Model selection is a key problem for combination model of network traffic,and in order to improve the forecasting accuracy of network traffic,this paper proposes a network flow combination model based on encompassing test and Support Vector Machine.A lot of single models are used to forecast the network traffic,and the merits of the model are defined by mean square error of the forecasting results,and then the appropriate single model is selected by encompassing test,and the single model prediction results are combined by Support Vector Machine to get the final forecasting result of network traffic,and the performance of model is tested by the simulation experiment.Τhe simulation results show that the proposed model can reduce the forecasting error and has improved the forecasting accuracy of network traffic.

network traffic;encompassing test;Support Vector Machine（SVM）;combination forecast

模型选择对网络流量组合预测结果至关重要，为了提高网络流量的预测效果，提出一种包容性检验和支持向量机相融合的网络流量预测模型（EΤ-SVM）。采用多个单一模型对网络流量进行预测，根据预测结果的均方根误差对模型优劣进行排序，通过包容性检验，根据t统计量检验选择最合适的单一模型，采用支持向量机对单一模型预测结果进行组合得到最终预测结果，通过仿真实验对模型性能进行测试。仿真结果表明，EΤ-SVM降低了网络流量的预测误差，预测精度得到了提高。

网络流量；包容性检验；支持向量机；组合预测

A

ΤP393.06

10.3778/j.issn.1002-8331.1301-0284

ZHENG Weiyong,FENG Guangli.Network traffic combination forecasting based on encompassing tests and Support Vector Machine.Computer Engineering and Applications,2013,49（15）：84-87.

郑伟勇（1978—），男，讲师，主要研究方向：计算机软件及应用、计算机网络、数据库技术；冯广丽（1973—），女，讲师，主要研究方向：计算机软件及应用、计算机网络通信。

2013-01-25

2013-04-22

1002-8331（2013）15-0084-04