复变函数的微分中值定理及其应用

郑利凯

(内蒙古民族大学数学学院，内蒙古通辽 028000)

我们知道实分析中有完整的微分中值定理，包括罗尔定理，拉格朗日定理，柯西中值定理等.但是实分析中的微分中值定理不能简单地推广到复变函数上来［1－3］.例如:

但如果中值点不限制在区间上，而是限制在一个圆形邻域内，实分析中的微分中值定理就可以推广到复变函数上来.主要的结论有:

文献［4］中得到以下结果:

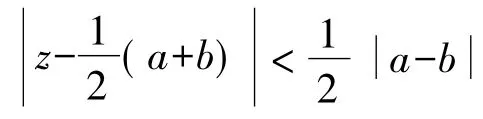
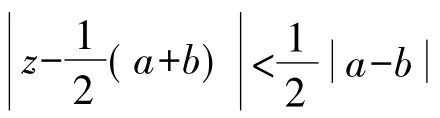
文献［5］中得到以下结果:

因为常见的函数大都是整函数，下面将这些解析函数中值定理的结论应用到整函数上，得到整函数的微分中值定理.

1 整函数的微分中值定理

根据上面的结论，可以推得以下定理:

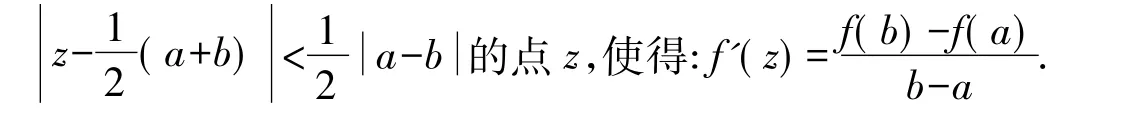
2 一个新的复变函数微分中值定理

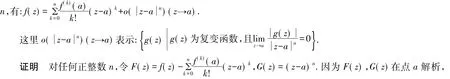
故F(z)，G(z)在点a的某邻域U(a)内解析，所以F(z)，G(z)在U(a)内存在任意阶导数.

又 F(a)=F'(a)=F″(a)= … =F(n)(a)=0，G(a)=G'(a)=G″(a)= … =G(n－1)(a)=0，G(n)(a)=n!.对F(z)，G(z)连续运用定理5，总共n次，得到:

3 复变函数微分中值定理的应用

复变函数的微分中值定理有着广泛而灵活的应用，下面就定理证明和计算复函数不定式极限两个方面加以论述.

3.1 定理的证明

解析函数的高阶导数定理是复变函数理论中一个及其重要的定理，一般著作都以积分不等式估计积分模的上限加以证明，下面用复变函数的微分中值定理来证明.

解析函数的高阶导数定理(柯西积分公式的推广)［6］设函数f(z)在简单闭曲线C所围成的闭区域D内解析，而在=D∪C上连续，则f(z)的各阶导函数均在D内解析，对D内任一点z，有:

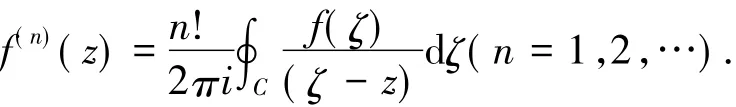
证明考虑n=1的情形.根据柯西积分公式有:

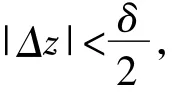
现假设n=k时命题成立，下面来推证n=k+1时命题也成立.

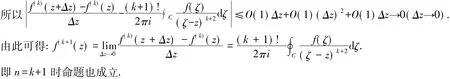
3.2 计算不定式极限

运用新得到的两个复变函数微分中值定理，即定理5，定理6，可以方便快捷地计算复变函数不定式的极限.

［1］李颖.复变函数的中值定理(英文)［J］.湘潭大学自然科学学报，1999(4):125－129.

［2］曾韧英.关于复变函数的中值定理［J］.重庆师范大学学报:自然科学版，1998，S1:46－47.

［3］李晓玲.微分中值定理在复数域内的推广［J］.佳木斯大学学报:自然科学版，2009(5):791－792.

［4］蒋润荣.Grace定理的推广［J］.数学杂志，1991(1):61－63.

［5］苏子安.复函数的微分中值公式［J］.数学的实践与认识，1992(4):90－92.

［6］钟玉泉.复变函数论［M］.3版.北京:高等教育出版社，2004:132－147.