四元数矩阵方程AX=B的反问题

黄 莉，刘丁酉

(1.武汉商业服务学院信息工程系，湖北武汉 430056;2.武汉大学数学与统计学院，湖北武汉 430072)

自文献［1－2］于1982年提出线性方程组AX=B的反问题以来，使得人们对反问题的研究日益关注，而近年来，随着四元数和四元数矩阵在数学和其他学科的应用日益广泛，四元数矩阵方程及其反问题的研究也就成为一个重要的课题，文献［3－4］都对四元数矩阵方程作了详尽讨论，而对四元数矩阵方程反问题的研究也做出了些很好的结果［5］.本文主要讨论四元数矩阵方程AX=B的反问题具有亚正定阵解的充要条件，以及此解存在的一般形式.

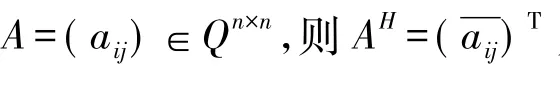
定义 1［4］设 A∈Qn×n，若对于任何 0≠x∈Qn×1，都有 Re(xHAx)＞0，则记 A∈P，称 A 为四元数体上的实

In部正定阵或亚正定阵.

定义2［6］设A∈Qn×n，若AAH=AHA，则称A为四元数体上的正规矩阵.

注:特别地，①AH=A时，正规矩阵A为Q上的自共轭阵;②AAH=AHA=In时，正规矩阵A为Q上的酉矩阵.

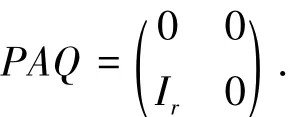
所谓四元数矩阵方程AX=B的反问题，就是指对于四元数矩阵方程AX=B，给定了X和B，求满足一定条件的四元数矩阵 A，使得 AX=B，其中 A∈Qn×n，X，B∈Qn×m.

1 亚正定矩阵反问题

2 主要结果

［1］李森林.几类直接控制系统绝对稳定的充要条件［J］.科学通报，1982(10):581－582.

［2］李文亮.四元数矩阵［M］.长沙:国防科技大学出版社，2002:97.

［3］王卿文.关于体上矩阵方程AX=B的解［J］.数学研究与评论，1995，15(2):249－252.

［4］王宜举.矩阵方程AX=B的实部正定解［J］.数学研究与评论，1998，18(2):315－316.

［5］王开民，刘永辉.四元数酉矩阵的反问题［J］.山东师范大学学报，2004(2):19－22.

［6］刘丁酉，黄莉.四元数矩阵与域上矩阵的几点差异［J］.湖北民族学院学报:自然科学版，2007，25(2):121－124.