Pb2H和PbH2分子的势能函数

朱 瑜，方 芳，马大柱，蒋 刚，朱正和

(1.湖北民族学院 理学院，湖北 恩施445000;2.湖北民族学院 信息工程学院，湖北恩施445000;3.四川大学原子与分子物理研究所，四川成都610065)

近年来的研究表明在钯中加入Y、Ag、Pb等元素能大大提高渗氢速率，因此钯的二元和多元合金的研究与开发是研究人员关注的热点［1－3］.目前已从理论上对钯铅混合团簇的结构和性质进行了研究［3－4］，但是对于铅参与渗氢过程的动力学行为和纯化氢的微观机理的研究还未见报道.本文对Pb2H、PbH2分子的结构进行优化，导出其分析势能函数，作出相应的伸缩振动和旋转振动势能图，为进一步了解其分子反应动力学作基础工作.

1 计算方法

本文采用Gaussian98程序［5］，用密度泛函B3LYP方法，对Pb2H和 PbH2分子体系的结构进行了优化，其中对氢原子采用的是6－311++G＊＊全电子基函数，对铅原子采用的是收缩价基组 LANL2DZ，即采用LANL2DZ相对论有效原子实势(RECP)［3－4］取代铅原子内层78个电子，铅原子价电子层的4个价电子(6s26p2)采用LANL2DZ双Zata基组描述.使用多体展式理论［6－7］导出势函数的可能参数，以此确定Pb2H和PbH2分子势函数的解析表达式，作出相应的伸缩振动和旋转振动势能图.

2 结果与分析

2.1 Pb2H分子的多体项展式势能函数

Pb2H分子的基态结构具有C2V对称性，其结构参数见表1.Pb2H分子还有一种亚稳态结构，具有C∞v对称性，核间距 RHPb=0.176 06 nm，RPbPb=0.271 70 nm，∠HPbPb=180.0 °，离解能 De=－3.868 19 eV.基态Pb2H(2A1)分子可能的离解通道为:

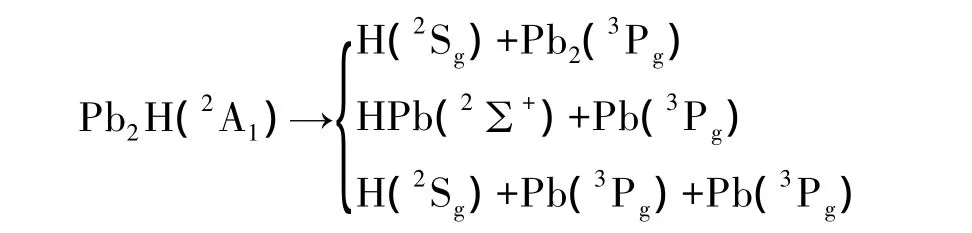
表1 Pb2H(C2V，2A1)和PbH2(C2V，1A1)分子的结构与性质参数Tab.1 Structure and properties parameters of Pb2H(C2V，2A1)and PbH2(C2V，1A1)

因为Pb2H分子和PdPb2分子［4］有相似的结构特征，本文选取相同的参考结构(R01=RHPb=0.20016nm，R02=R03=(RHPb+RPbPb)/2=0.24115 nm作为参考坐标).Pb2H分子的多体项展式势能函数取与PdPb2分子相同的形式［4］，其中所需的两体项势能函数采用Murrell－sorbie势能函数［7］，其参数分别见文献［8］和文献［4］.对势能表面进行非线性优化，确定出三个非线性系数(γ1，γ2，γ3)和 10 个线性系数(C1，C2，C3，C4，C5，C6，C7，C8，C9，C10)，由此可确定Pb2H 分子的分析势能函数.计算结果列于表2.

图1和图2是Pb2H分子的分析势能函数的等值势能图，图中清晰地再现了Pb2H分子的基态和亚稳态结构.图1是Pb2H分子的伸缩振动势能图，采用固定∠PbHPb=89.62469°，表现了两个H－Pb键的伸缩振动.此图准确地展现出Pb2H分子的基态结构，在RHPb=0.20016 nm时，出现一势阱，能量为－4.35313eV，这对应于Pb2H分子的基态.图中无鞍点存在，这说明Pb接近H是容易进行的无域能反应.图2是Pb2H分子的旋转势能图，采用把Pb－Pb键固定在X轴上，取RPbPb=0.28214nm，让H原子绕Pb－Pb键旋转.图中准确地展现出H原子内迁移的详细过程，清晰地描绘出Pb2H分子的基态和亚稳态结构.当H原子位于X轴上±0.3～0.4nm时，所对应的能量为－3.86819eV，这对应于Pb2H分子C∞v对称性的线性结构.当H原子绕Pb－Pb键旋转时，大约需要克服1.04819eV的能垒，最终形成Pb2H分子的基态结构.

表2 Pb2H(C2V，2A1)分析势能函数的三体项参数Tab.2 The three－body parameters of analytic potential energy function of Pb2H(C2V，2A1)

图1 Pb2H的伸缩振动势能图(固定∠PbHPb=89.62469°)Fig.1 Stretched vibrational contours of potential energy function for Pb2H(PbHPb=89.62469 °)

图2 Pb2H的旋转势能图(固定RPbPb=0.28214 nm)Fig.2 Rotational contours of potential energy function for Pb2H(RPbPb=0.28214 nm)

2.2 PbH2分子的多体项展式势能函数

PbH2分子的基态结构具有C2V对称性，其结构参数见表1.基态PbH2(1A1)分子可能的离解通道为:

因为PbH2分子和Pb2H分子有相似的结构特征，本文选取相同的参考结构(R01=RPbH=0.18231 nm，R02=R03=(RPbH+RHH)/2=0.22039nm作为参考坐标)，PbH2分子的多体项展式势能函数取与Pb2H分子相同的形式.对势能表面进行非线性优化，确定出三个非线性系数(γ1，γ2，γ3)和十个线性系数(C1，C2，C3，C4，C5，C6，C7，C8，C9，C10)，由此可确定 PbH2分子的分析势能函数.计算结果列于表 3.

图3和图4是PbH2分子的分析势能函数的等值势能图，图中清晰地再现了PbH2分子的基态结构特征.图3是PbH2分子的伸缩振动势能图，采用固定∠HPbH=90.285 70°，表现了两个Pb－H键的伸缩振动.此图准确地展现出PbH2分子的基态结构，在RPbH=0.18231 nm时，出现一势阱，能量为－5.37712 eV，这对应于PbH2分子的基态.图中无鞍点存在，这说明H接近Pb是容易进行的无域能反应.图4是PbH2分子的旋转势能图，采用把H－H键固定在X轴上，取RHH=0.25847 nm，让Pb原子绕H－H键旋转.图中准确地展现出Pb原子内迁移的详细过程，清晰地描绘出PbH2分子的基态结构.当Pb原子位于坐标(0，0.12859)时，所对应的能量为－5.37712 eV，这对应于PbH2分子的基态.图中无鞍点存在，这说明Pb接近H是容易进行的无域能反应.

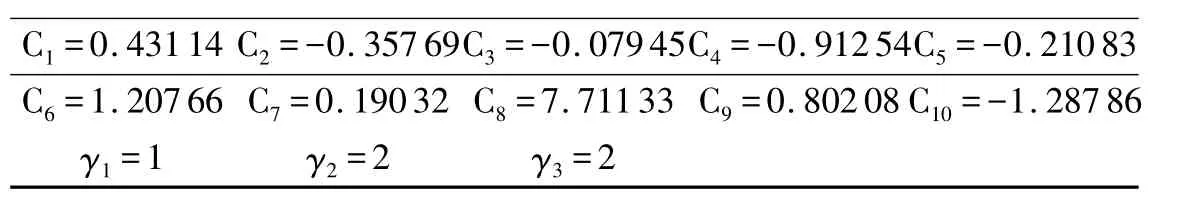
表3 PbH2(C2V，1A1)分析势能函数的三体项参数Tab.3 The three－body parameters of analytic potential energy function of PbH2(C2V，1A1)

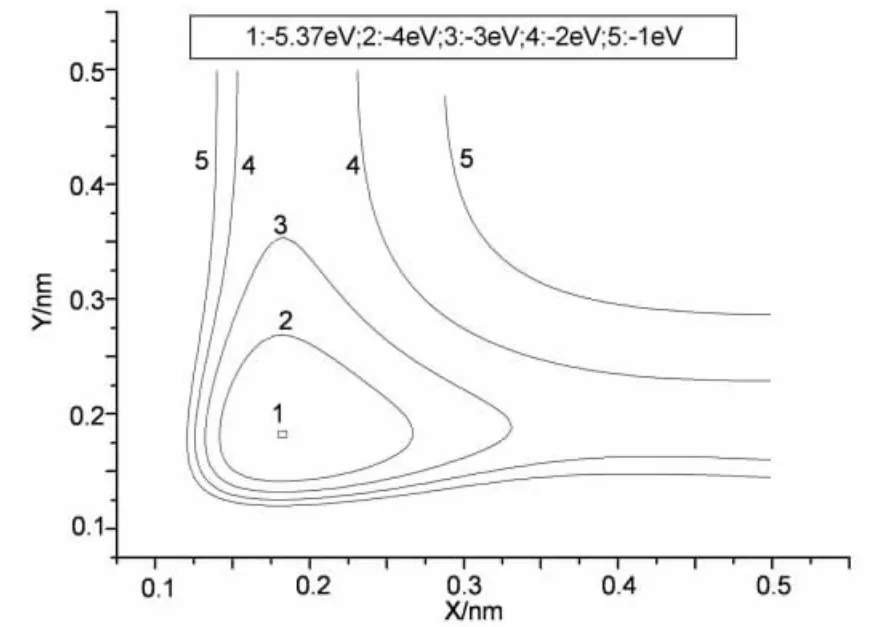
图3 PbH2的伸缩振动势能图(固定∠HPbH=90.28570°)Fig.3 Stretched vibrational contours of potential energy function for PbH2(HPbH=90.28570 °)

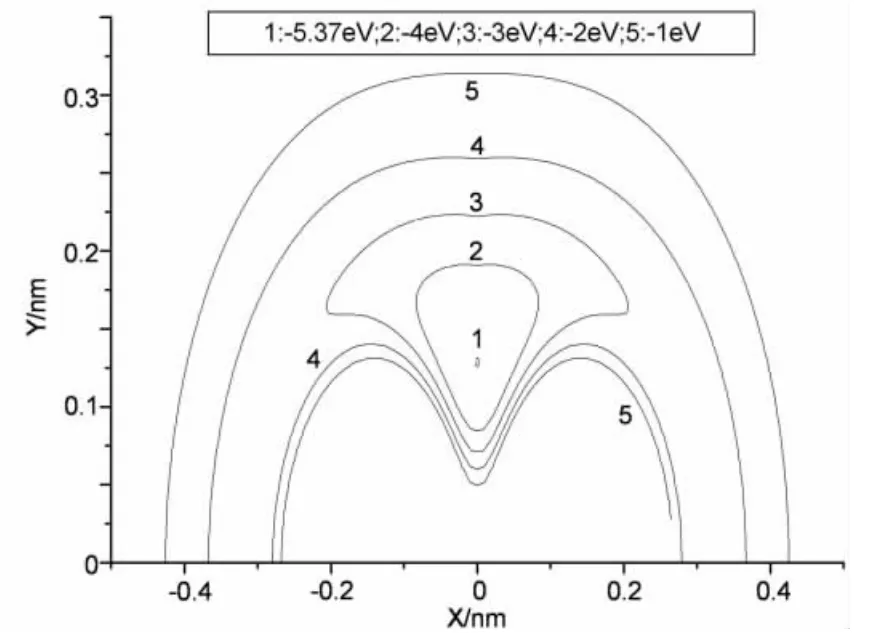
图4 PbH2的旋转势能图(固定RHH=0.25847 nm)Fig.4 Rotational contours of potential energy function for PbH2(RHH=0.25847 nm)

比较Pb2H和PbH2分子的伸缩振动势能图，发现不管是Pb接近H还是H接近Pb都是容易进行的无域能反应.比较Pb2H和PbH2分子的旋转势能图，发现H原子绕Pb－Pb键旋转的内迁移过程比Pb原子绕H－H键旋转的内迁移过程要复杂得多，这说明随着铅元素的含量增大，铅与氢反应的过程变得越来越复杂.

3 结论

本文采用Gaussian98程序，用B3LYP方法，对氢原子采用6－311++G＊＊全电子基函数，对铅原子采用收缩价基组LANL2DZ，分别对Pb2H和PbH2分子的结构进行了优化，得到Pb2H和PbH2分子的基态结构均具有C2V对称性，还得到Pb2H分子具有C∞v对称性的亚稳态结构.使用多体展式理论导出了势函数的十三个参数，从而确定出Pb2H和PbH2分子势函数的解析表达式，其伸缩振动和旋转振动势能图准确地复现了Pb2H和PbH2分子的稳定结构和能量关系，其中包括Pb2H分子的亚稳态结构.

［1］ 唐涛，陆光达.钯－氢体系的物理化学性质［J］.稀有金属，2003，27(2):278－285.

［2］ 倪羽，蒋刚，朱正和，等.PdYH 分子的结构与势能函数［J］.化学学报，2005，63(8):764－768.

［3］ 方芳，蒋刚，王红艳.PdnPbm(n+m≤5)混合团簇的结构与光谱性质［J］.物理学报，2006，55(5):2241－2248.

［4］ 朱瑜，方芳，蒋刚，等.Pb2、PdPb2分子的势能函数［J］.物理学报，2008，57(7):4134－4137.

［5］ Frisch M J，Trucks G W，Schlegel H B，et al.Gaussian 98(Revision A.9)［M］.Gaussian Inc，Pittsburgh PA，1998.

［6］ Murrell J N，Carter S，Farantos S C，et al.Molecular potential energy functions［M］.London:Mid－County Press，1984:29.

［7］ 朱正和，俞华根.分子结构与分子势能函数［M］.北京:科学出版社，1997:109.

［8］ 方芳，朱瑜，蒋刚，等.PdPbH分子的结构与势能函数［J］.原子与分子物理学报，2007，24(1):173－177.