采用转速离散惯性反馈的风力机转速特性研究

陈基和, 徐 立

（清华大学电机系电力系统国家重点实验室，北京 100084）

0 引言

随着风电机组装机容量日益增加，电网对风电机组的并网接入特性提出了更高的要求，迫使传统的双馈型[1]和全功率变换型变速恒频风电机组[2]不断地改进技术以满足电网的需求。受此影响，一些新概念电网友好型风电机组受到了越来越多的关注。电磁耦合调速风电机组是一种新型风电机组，其基本拓扑结构如图1所示。由于采用直接并网同步发电机，该型风电机组具备了与火电机组同等的并网特性[3]。电磁耦合器由一对内、外转子组成，两个转子之间通过受控的电磁转矩进行耦合，且相对转速可任意调节[4]。电磁耦合器将风电机组中的机械传动链分割为前、后两个独立的子系统。前者包括了风力机、升速齿轮箱和电磁耦合器的内转子；后者包括了电磁耦合器外转子和同步发电机。在前一个子传动链中，电磁耦合器的电磁转矩由变频器主动控制，它作为风力机的负载转矩对风力机的转速进行调节[5]。本文针对电磁耦合调速风电机组，主要研究在最大风能捕获过程中，采用转速离散惯性反馈的风力机转速特性。通过建立采用离散惯性反馈的风力机轴系动力学稳定分析模型，分析了风力机转速振荡与惯性时间常数和风速等参数的关系。并提出了惯性时间常数的设计原则。

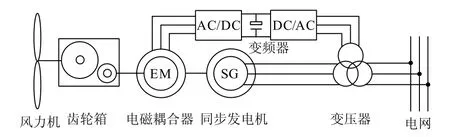
图1 基于电磁耦合器调速的风电机组结构示意图Fig. 1 Schematic of wind turbine based on electromagnetic coupling speed

1 风力机轴系动力系统模型

风力机轴系包括风力机轴、变速箱和与其相连的电磁耦合器转子轴。由于作用于风力机叶片的风速难以准确测量，当风电机组运行在最大风能捕获状态下，风力机的负载转矩，即电磁耦合器的电磁转矩的控制给定值，一般通过在预先设置的转速-转矩曲线查表获得。

1.1 转速连续反馈的风力机轴系动力系统模型

根据贝兹理论，风力机输出机械转矩为[6]

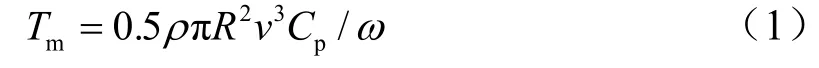
其中：ρ为空气密度；R为叶轮半径；v为风速；ω为风力机转速； Cp为风能利用系数；其模型为λ为叶尖速比。

当风电机组运行在最大风能捕获状态时，电磁耦合器预先设置的转速—转矩曲线可近似为

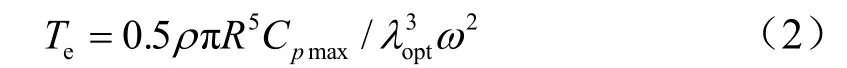
其中：maxpC为最大风能利用系数；optλ为最佳叶尖速比。

折算到低速端的风力机轴系运动方程为

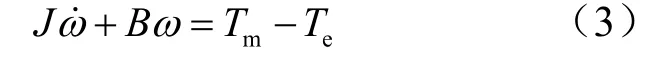
其中： J为折算后的风力机转动惯量；B为折算后的风力机阻尼系数。

当转速采用连续反馈时，电磁耦合器的给定转矩随着转速而连续变化。由式（2）可得，当确定了桨距角，为捕获最佳风能，负载转矩给定与转速的平方成正比。对于运动方程式（3），忽略B，当风能机械转矩等于电磁转矩时，转速位于平衡点，通过分析风能和电磁转矩特性，平衡点是稳定的，而且在最大风能捕获状态下，平衡点是唯一的，同时具有全局稳定性。

1.2 转速离散反馈的风力机轴系动力系统模型

当转速采用离散反馈时，可设离散控制周期为T，转速反馈选取上一个周期转速ω的终值（即本周期的初值），并保持不变。令 t ∈[0,T]，n= 0 ,1,2,，则第n个T内的风力机运动方程为

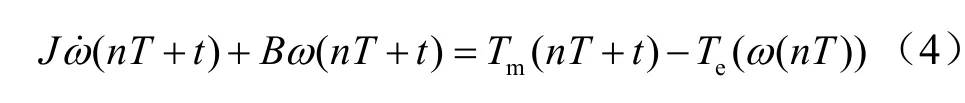
设 xn=ω(n T)，则X = { xn}∞n=0是ω依次在t=nT, n =0,1,2,,∞的采样值。即可得ω曲线的庞加莱映射为 H : R → R , xn+1= H(xn)，庞加莱映射的特征指数为： z = ∂H (x) = ∂xn+1/∂ xn，庞加莱映射的特征指数为式（5）的解。

连续的ω曲线和离散的庞加莱映射 X ={ xn}

∞n=0具有相同的动力学特性，即可通过讨论X特性而获得ω的特性。当 x*= H(x*)，则x*为平衡点。当它们的特征指数的绝对值小于1时，平衡点是稳定的。

1.3 转速惯性反馈的风力机轴系动力系统模型

在风电机组实际应用中，为了保证发电机的稳定运行，要求转速ω尽量平稳。可采用惯性环节对ω滤波后的τω作为转速反馈[7]。相应传递函数如式（6）。

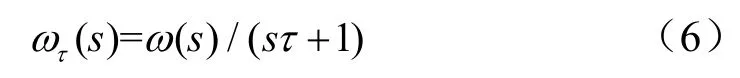
其中，τ为惯性时间常数，相应的电磁耦合器预先设置的转速—转矩曲线可近似为

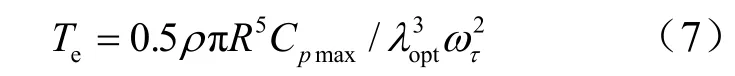
当转速离散反馈时，第n个T内的转速反馈为

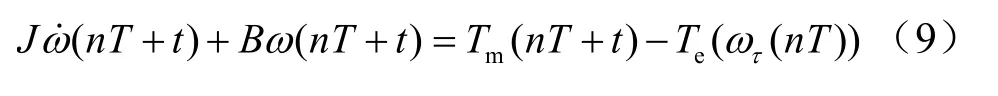
2 风力机转速稳定性分析

风电机组在运行的过程中，会遇到风速变化、电磁耦合器给定转矩跟随存在控制误差，还有为调节发电机功角变化而产生的电磁耦合器给定转矩的变化等多种扰动。这些扰动在某些情况下是短暂的，会造成风力机转速偏离原先的平衡点。当平衡点是稳定的，风力机转速会从偏离点，经过一段时间的暂态过程后，收敛于平衡点。通过分析在不同的转速惯性反馈时间常数、转速扰动偏差、运行风速下，风力机转速暂态过程以及是否收敛与平衡点的变化过程，探寻上述参数对转速稳定性的影响。

1.5 MW 的机组运行在最大风能捕获状态下的风速范围为4 m/s至13 m/s，风力机转速范围为0.73 rad/s至2.2 rad/s。离散控制周期T=20 ms，风力机轴系运动方程的参数为： c1=0.5176， c2=116，c3=0.4， c4=5， c5=21， c6=0.0068， c7=0.035，c8=0.08，R=33.75 m，J=3 098250 kgm2，B=0，λopt=8.1， Cpmax=0.48。

2.1 惯性时间常数对转速稳定性的影响

当风速v为6 m/s时，对于无惯性环节的转速反馈，由式（4）可求得转速平衡点*ω为1.44 rad/s，由式（5）可求得庞加莱映射的特征指数为0.642，特征指数小于 1，因此平衡点是稳定的。由于控制周期远小于风力机的机械时间常数，式（4）和式（3）具有相同的稳定性。

当转速在单点扰动下，转速扰动偏离Δω*为0.1 rad/s时，即转速初值 ω0= ω*+Δω*为1.54 rad/s，采用转速离散反馈模型式（4）和式（9），分别从转速ω随时间变化的曲线、转速ω与转速反馈ωτ的转速差 Δω = ω − ωτ随时间变化的曲线、转速ω与风力机转矩差 Δ Tme= Tm( ω) − Te(ωτ)的相轨迹等方面探讨不同的惯性时间常数τ对系统稳定性的影响。

首先，观察不同惯性时间常数对转速曲线的影响。不同τ的ω曲线如图2所示，当τ为3 s的时候，ω曲线位于无转速惯性反馈时线的左边相邻处，其暂态响应有减小趋势；当τ为100 s，ω曲线会迅速的下降并出现超调，系统的暂态时间反而增加；当τ为1 500 s，ω曲线迅速下降并不再收敛到平衡点。可见，τ不仅影响了ω从扰动偏差恢复到平衡点的动态响应特性，还影响了系统的稳定性。

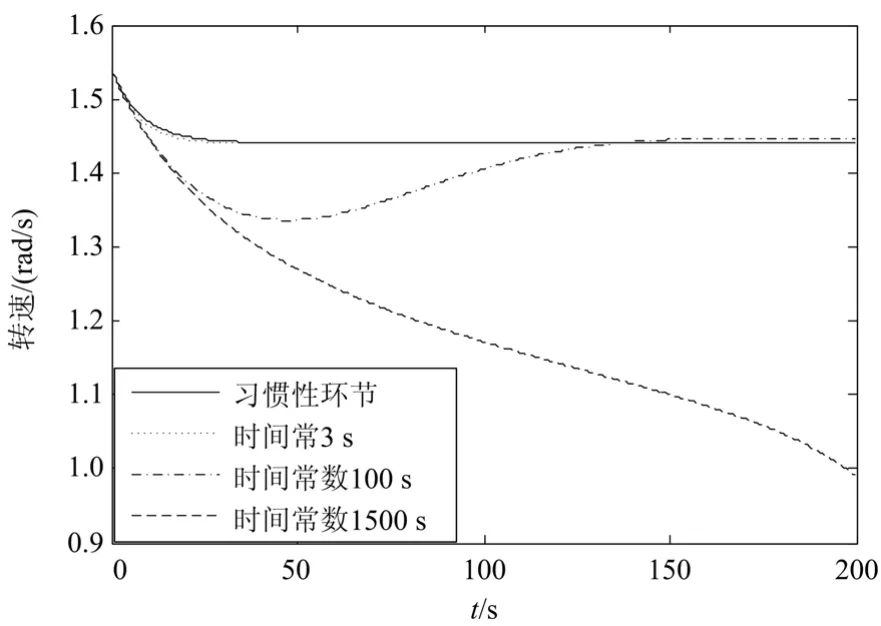
图2 不同惯性时间常数下转速变化曲线Fig. 2 Curve of rotational speed varying with different inertia time constants

其次，观察不同惯性时间常数对转速差曲线的影响。不同τ的 Δω 曲线如图3所示，当τ为3 s时，Δω 先小于0，随后会出现极小值，最后趋于0，对应于ω单调地趋于平衡点；当τ为100 s时，Δω同样先小于0，随后会出现极小值，但在过0后，还出现极大值，最后趋于 0，对应于ω为超调振荡地趋于平衡点；当τ为1 500 s时，Δω一直小于0，系统不收敛。从上述不同的τ对应的Δω的变化，可以看出，虽然ω与ωτ的初值相同，但由于惯性环节的作用，ωτ的变化要滞后于ω变化，当扰动为正偏差，则 Δω 为负值。当 Δω 最终趋于0时，则系统是稳定的，转速收敛于平衡点，否则系统是发散的。进一步分析还可以看出，当Δω存在一个极值，ω单调地趋于平衡点；随着τ的增加，Δ ω 的极值的绝对值也在增大，当Δω大于0.027 rad/s时，Δω会出现正负两个极值，ω为超调振荡的趋于平衡点；当Δω进一步增大，超过0.39 rad/s时，Δω不存在极值，系统是不稳定的。可见，Δω 的大小可作为判断ω暂态特性及其稳定性的重要指标。

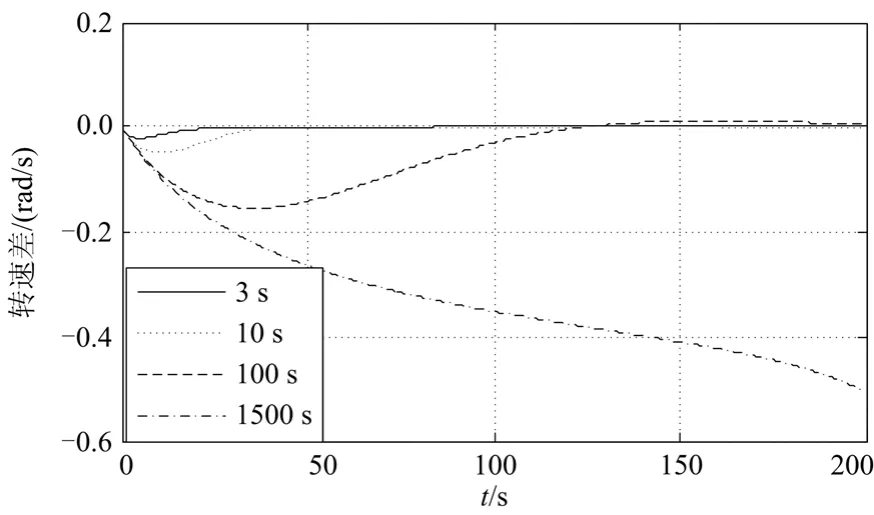
图3 不同惯性时间常数下的转速差曲线Fig. 3 Curve of rotational speed difference under different inertia time constants

最后，观察不同惯性时间常数对转速—转矩差相轨迹的影响。不同τ的ω—ΔTme相轨迹如图4所示，相轨迹所描述的特性和图3相对应，当τ为3 s时，相轨迹从初始状态直接运动到平衡点，转速收敛于平衡点且没有超调振荡。当τ分别为20 s和100 s时，相轨迹从初始状态经过一个弧形回到平衡点，且后者比前者具有更大超调振荡。当τ为1 500 s时，相轨迹不再回到平衡点，系统不稳定。进一步分析ΔTme可以看出，由于ωτ滞后于ω的值，随着τ的增加，ΔTme变化减缓，从而造成ω的快速下降，相应地Δω快速增加，从而超调振荡加剧，直至超过Δω的极限值，ΔTme不再趋向0，系统失稳。

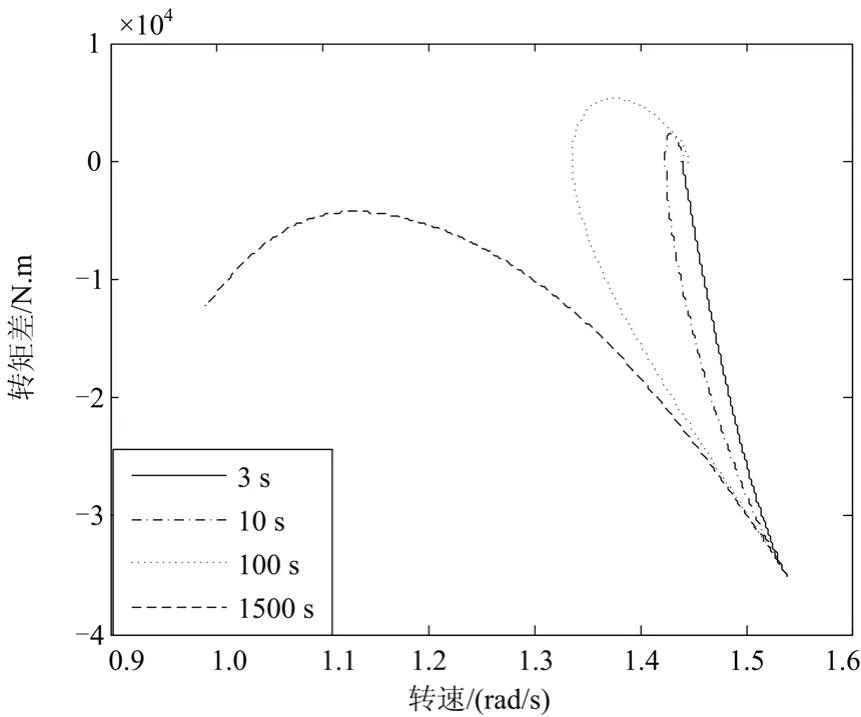
图4 不同惯性时间常数下的转速-转矩相轨迹Fig. 4 Speed-torque phase trajectory under different inertial time constants

2.2 转速扰动偏差对转速稳定性的影响

选取v为6 m/s，则转速平衡点ω*为1.44 rad/s，采用转速离散反馈模型式（4）和式（9），分析当τ为100 s时，不同转速扰动偏差Δω*的ω—ΔTme相轨迹特性。如图5所示，当Δω*为0.1 rad/s和0.2 rad/s时，相轨迹从初始状态经过一个弧形回到平衡点，且后者比前者具有更大超调振荡。当Δω*为0.3 rad/s和0.4 rad/s时，相轨迹不再回到平衡点，系统出现不稳定。对比4条相轨迹可看出，尽管它们在初始时接近平行，但较大Δω*的相轨迹对应于较大的ΔTme初值，从而造成ω的较快下降，相应地Δω有较大的增加。由于τ为100 s时，系统的稳定裕度较低，当Δω*较大时， Δω 会超过极限值，使系统失去稳定性。

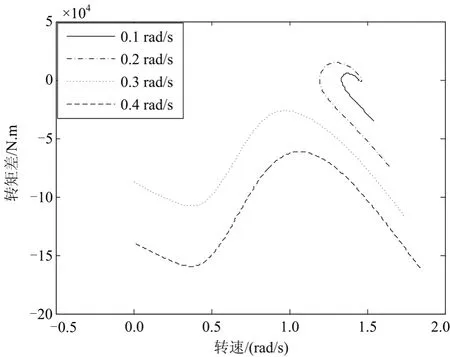
图5 不同转速扰动偏差下的转速-转矩相轨迹Fig. 5 Speed-torque phase trajectory under different speed disturbance deviation

2.3 运行风速对转速稳定性的影响

选取τ为100 s，采用转速离散反馈模型式（4）和式（9），分析不同风速对风力机转速特性影响。当转速扰动偏差Δω*分别皆为0.3 rad/s和各平衡点ω*的20%时，不同v的ω—ΔT相轨迹如图6（a）

me和图6（b）所示，相同v的相轨迹在两图中的特性是相反的。对于v为4 m/s和5 m/s，当Δω*为ω*的20%时，相轨迹趋于ω*为0.96 rad/s和1.2 rad/s；当Δω*为0.3 rad/s，即ω*的31.3%和25%时，系统不稳定。对于v为7 m/s和8 m/s，当Δω*为ω*的20%时，系统不稳定；当Δω*为0.3 rad/s，相当于ω*的17.9%和15.6%时，相轨迹趋于ω*为1.68 rad/s和1.92 rad/s。由此可得，在相同的Δω*的相对值的情况下，随着v的增加，转速稳定裕度减少，甚至出现不稳定。

图6 不同风速下的转速-转矩相轨迹Fig. 6 Different wind speed-torque phase trajectory

2.4 增强转速稳定性措施

从上述分析可以得出，对风力机转速的暂态过程及其稳定性，主要取决于惯性时间常数τ和转速扰动偏差Δω*。对于v为6 m/s，当Δω*为0.1 rad/s，τ为1000 s时，系统稳定；但当Δω*为0.3 rad/s，τ为100 s时，系统不稳定。对于极端情况：v为4 m/s，ω*为0.96 rad/s，Δω*为1.1 rad/s，则τ为20 s以内，系统稳定。因此，为保证系统在运行风速范围内抵御可能出现的最大Δω*，τ应小于稳定临界值，以使得系统留有适当的稳定裕度。

根据2.1小节对转速ω与转速反馈ωτ的转速差Δω的分析结果，可以得出对Δω进行限幅，有利于增大系统的稳定裕度。当 Δω 限幅绝对值为0.2 rad/s时，对于上述的极端情况：v为4 m/s，ω*为0.96 rad/s，Δω*为1.1 rad/s，当τ为100 s时，系统稳定。当减少限幅绝对值，可获得更多的稳定裕度。

3 持续扰动下惯性环节离散反馈的转速特性

当风力机受到风速持续扰动时，风力机轴系转速会出现振荡，本节分析不同惯性时间常数的惯性环节对不同频率和幅值的阵风扰动下的转速振荡抑制效果。

考虑风速持续变化，假设风电机组受到持续的阵风影响，给定风速随时间周期变化风速模型为

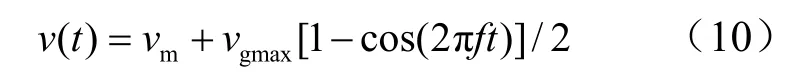
其中： vm为初始风速； vgmax为阵风最大值；f为阵风频率。

3.1 不同频率风速扰动下的转速振荡特性

设 vm为7 m/s， vgmax为1 m/s，由于风力机轴系存在较大的机械惯性，对于频率高于1 Hz的阵风，转速的振荡小于0.01 rad/s。

首先，选取f为0.1 Hz，不同τ的ω曲线如图7所示。当无惯性调节时，ω振荡幅值为0.103 rad/s，此时200 s内平均输入功率0.532 MW；当τ为4s时，ω振荡减小至0.04 rad/s，约为无惯性环节时的38.9%，此时200 s内平均输入功率0.530 MW；当τ为40 s时，ω振荡进一步减小至0.002 rad/s，约为无惯性环节时的1.9%，但其暂态的过程变长，此时200 s内平均输入功率0.518 MW。

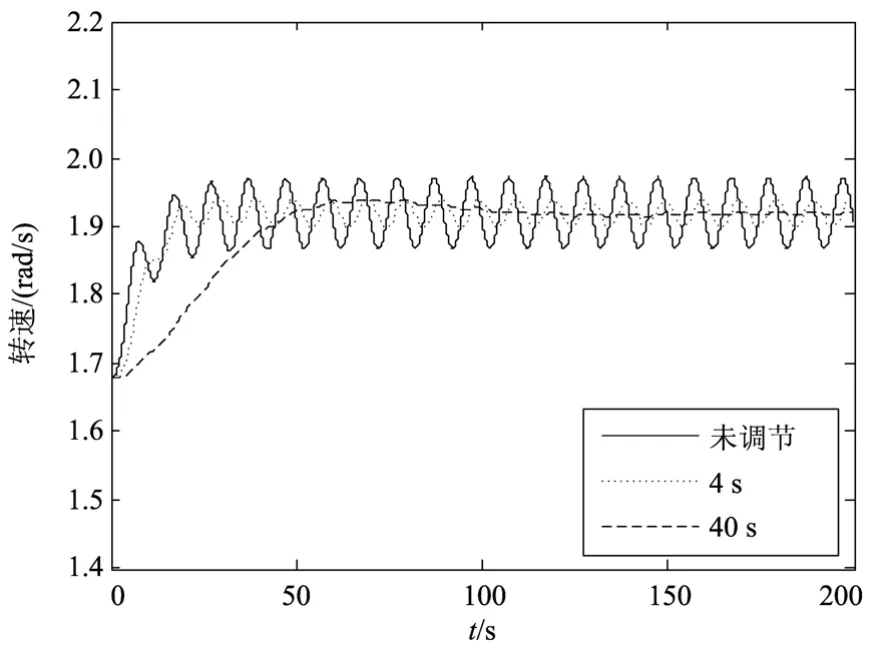
图7 幅值1 m/s频率0.1 Hz惯性调节转速曲线Fig. 7 Inertia adjust speed curve when the amplitude is 1m/s and the frequency is 0.1 Hz

其次，选取f为0.01 Hz，不同τ的ω曲线如图8所示。当无惯性调节时，ω振荡幅值为0.436 rad/s，此时2 000 s内平均输入功率0.539 MW；当τ为40 s时，ω振荡幅值略微减小至0.381 rad/s，约为无惯性环节时的87.4%，此时2 000 s内平均输入功率0.525 MW；当τ为400 s时，ω振荡幅值进一步减小至0.035，约为无惯性环节时的8%，此时2 000 s内平均输入功率0.508 MW；当τ为1 000 s时，ω振荡幅值进一步减小至 0.014，约为无惯性环节时的3.2%，此时2 000 s内平均输入功率0.492 MW。

对比图7和图8，可以看到，随着阵风频率的减少，轴系机械惯性对转速振荡作用降低，需要增大惯性时间常数，以达到抑制转速振荡的幅值，但同时也会造成动态响应变慢。对于0.01 Hz级以上的阵风扰动，当惯性时间常数为阵风周期的4倍时，可基本抑制转速振荡的幅值至10%以内，而且对风力机的输出功率影响较小。

图8 风速频率0.01 Hz惯性调节曲线Fig. 8 Inertia tuning curves when the wind speed frequency is 0.01 Hz

3.2 不同幅值风速扰动下的转速振荡特性

设 vm为7 m/s， vgmax为0.5 m/s，f为0.1 Hz，不同τ的ω曲线如图9所示，当无惯性调节时，ω振荡幅值为 0.05 rad/s，此时 200 s内平均输入功率0.441 MW；当τ为4 s时，ω振荡幅值减小至0.02 rad/s，约为无惯性环节时的40%，此时200 s内平均输入功率0.440 MW；当τ为40 s时，ω振荡幅值进一步减小至0.002 rad/s，约为无惯性环节时的4%，此时200 s内平均输入功率0.435 MW。

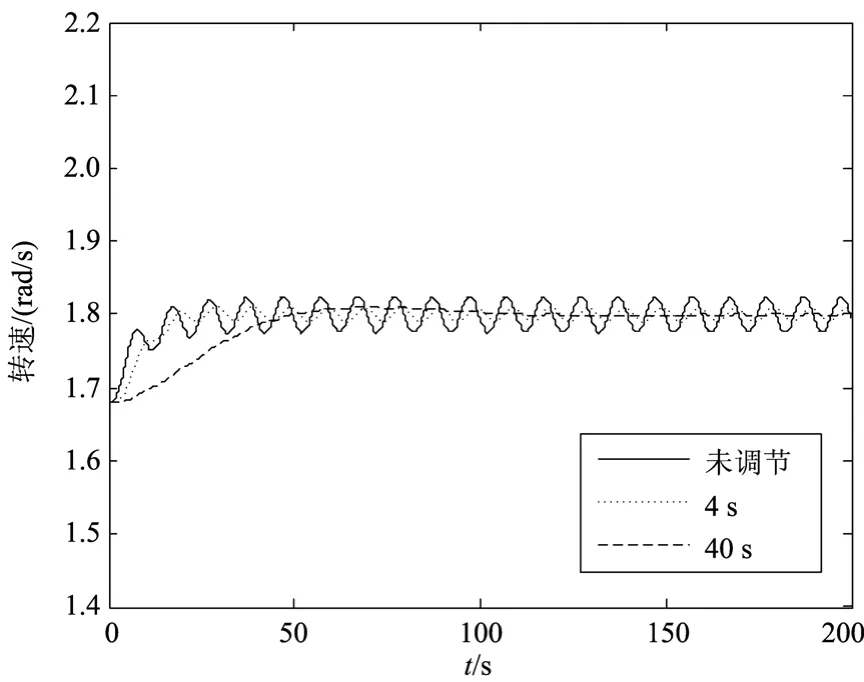
图9 扰动幅值0.5m/s惯性调节曲线Fig. 9 Inertial adjustment curve when the perturbation amplitude is 0.5m/s

对比图7与图9，可以看到，在不同幅值的风速扰动下，当τ为4 s时，转速振荡幅值调节至38.9%和40%；当τ为40 s时，转速振荡幅值调节至0.002 rad/s。因此，对应不同风速幅值的扰动，同样的τ具有相近的调节效果。

3.3 惯性时间常数的选取

增大惯性时间常数，有利于抑制转速振荡的幅值，但同时会增大转速的动态响应时间，当惯性时间常数足够大时，系统会失去稳定性。因此，在实际的工程中，惯性时间常数的选取原则如下：

首先，要满足风电机组需抑制的最低阵风扰动频率的要求。以本文风电机组为例，其自身的机械惯性可以基本抑制1Hz以上的风速扰动。对于更低频率的风速扰动，可选取惯性时间常数为需抑制的阵风周期的40%至4倍之间，转速振荡幅值的抑制效果达到未加惯性环节的40%至5%。

其次，要保证系统具有足够的稳定裕度。以本文风电机组为例，当满足最低阵风扰动频率抑制要求的惯性时间常数大于 15时，应对转速ω与转速反馈τω的转速差ωΔ进行限幅，限幅值越小，则系统的稳定裕度越大。

最后，要满足风电机组动态响应时间的要求。以本文风电机组为例，惯性时间常数要小于动态响应时间。

4 结论

本文通过理论推导与仿真计算，研究了电磁耦合器调速的变速恒频风电机组，运行在最大风能捕获状态，在单点扰动和持续扰动下，采用转速离散反馈惯性调节控制的风力机转速特性。

在单点扰动下，风力机转速的暂态过程及其稳定性，主要取决于惯性时间常数τ和转速扰动偏差Δω*。小幅增加τ有利于缩短风力机转速的暂态时间，但τ和Δω*过大反而会引起超调振荡而加大暂态时间，甚至有可能失去稳定性。通过观察转速ω与转速给定ωτ之差Δω的变化，可判定系统稳定性。对于较大的τ和Δω*，相应较大的Δω极值，当Δω极值超出稳定临界值时，系统失去稳定性。为此，可通过对Δω进行限幅的方式来改善系统的稳定性，限幅值越小，系统稳定裕度越大。

在持续扰动下，增大惯性时间常数，有利于抑制转速振荡的幅值，但同时会增大转速的动态响应时间。为抑制较低频率的风速扰动，可选取惯性时间常数为需抑制的阵风周期的40%至4倍之间，转速振荡幅值的抑制效果达到未加惯性环节的40%至5%，而且对风力机的输出功率影响较小。同时，给出了综合考虑系统稳定性、转速抑制需求和动态响应时间的惯性时间常数的基本选取原则。

[1] 王定国, 张红超. 双馈型风力发电机低电压穿越的分析研究[J]. 电力系统保护与控制, 2011, 39(17): 70-73.WANG Ding-guo, ZHANG Hong-chao. Analysis and research of low voltage ride through for doubly fed wind power generator[J]. Power System Protection and Control,2011, 39(17): 70-73.

[2] 李戈, 宋新甫, 常喜强. 直驱永磁风力发电系统低电压穿越改进控制策略研究[J]. 电力系统保护与控制,2011, 39(12): 74-78.LI Ge, SONG Xin-fu, CHANG Xi-qiang. Improved control theory for low voltage ride-through of permanent magnet synchronous generator[J]. Power System Protection and Control, 2011, 39(12): 74-78.

[3] 叶杭冶. 风力发电机组的控制技术[M]. 北京: 机械工业出版社, 2002: 130-140.YE Hang-zhi, Control technology of wind power generating systems[M]. Beijing: China Machine Press,2002: 130-140.

[4] 周强明. 基于电磁耦合器调速的变速恒频风力发电机组[D]. 北京: 清华大学, 2009.ZHOU Qiang-ming. VSCF wind turbine generator based on an electromagnetic coupler[D]. Beijing: Tsinghua University, 2009.

[5] 马洪飞, 徐殿国, 苗立杰. 几种变速恒频风力发电系统控制方案的对比分析[J]. 电工技术杂志, 2000(10):1-4.MA Hong-fei, XU Dian-guo, MIAO Li-jie. Scheme comparison ＆amp; analysis of four types VSCF wind power generation system[J]. Electrotechnical Journal, 2000(10):1-4.

[6] 刘钰山, 葛宝明, 毕大强. 基于改进的直接转矩控制的风力机模拟系统[J]. 电力系统保护与控制, 2010,38(18): 140-144.LIU Yu-shan, GE Bao-ming, BI Da-qiang. Improved direct control based wind turbine simulation system[J].Power System Protection and Control, 2010, 38(18):140-144.

[7] Ion Boldea, Lucian Tutelea, Ioan Serban. Variable speed electric generators and their control: an emerging technology[J]. Journal of Electrical Engineering, 2002, 3:20-28.