基于灰色离散Verhulst模型理论的电力中长期负荷预测研究

张 成，滕 欢, 付 婷

（四川大学电气信息学院， 四川 成都 610065)

0 引言

电力系统负荷预测是指根据电力负荷本身或经济、社会、气象等相关因素的历史数据，探索电力负荷发展变化规律，以及寻求电力负荷与各种相关因素之间的内在联系，从而对未来的电力负荷进行科学的预测[1-2]。从这一点出发，现有的负荷预测研究方法分成了两大类：一类是仅从负荷历史数据出发，建立起预测模型，这类方法有回归分析法、动平均法、指数平滑法和灰色预测法等[3]；另一类则考虑影响负荷变化的相关因素，建立起预测模型，如多元回归分析法[4]、考虑气象因素的预测法[5]等。其中灰色预测模型及其相关改进模型在负荷预测中扮演着非常重要的角色，其应用范围包括短期负荷预测[6-7]和中长期负荷预测[8-10]。

文献[11]通过分析城市年用电量发展规律，总结出三种类型的城市用电量发展趋势，并指出传统GM(1,1)模型对具有饱和特性和按“S型”规律增长的负荷进行预测时会产生较大的误差。为了对按“S型”规律增长的负荷或系统作出更加准确的预测，很多学者提出了灰色Verhulst模型及其相应的改进模型[12-15]。文献[12-13]是站在应用的角度对灰色Verhulst模型做了改进，提高了其在负荷预测中的预测精度，文献[14-15]则是站在建模机理的角度，借鉴GM(1,1)模型的相关发展成果和研究经验提出了新的灰色Verhulst模型。

根据离散灰色模型的理论[16]，离散灰色模型可以克服传统灰色模型中由于参数估计采用离散形式的方程，模拟和预测则采用连续形式的方程，而造成的系统误差。并且在离散模型中，发展系数可以任意的取值，这就大大地扩展了灰色预测模型的适应范围。文献[15]正是借鉴了这一离散化思想，基于原始数据序列一阶累加生成序列的倒数序列直接建立起灰色离散Verhulst模型。但通过深入分析发现该倒数序列呈现出非齐次增长规律，对其直接建立起形如非齐次指数的离散灰色模型的灰色离散Verhulst模型缺乏理论依据。

基于此，本文深入分析了原始数据序列一阶累加生成序列的倒数序列的变化规律，并通过借鉴离散灰色模型理论构建了一种新的灰色离散Verhulst模型。通过分析表明该模型符合离散灰色模型的构建过程，具有严密的理论依据。根据灰色预测理论的预测特点，采用等维灰数递补预测法对灰色离散Verhulst模型进行改进。最后通过实例论证了本文方法的正确性和有效性。

1 经典灰色Verhulst模型

灰色Verhulst模型主要用来描述具有“S型”变化规律的过程，因此，可以用于预测呈现“S型”变化规律的一类电力负荷，其建模过程如下[12,17]。

则称

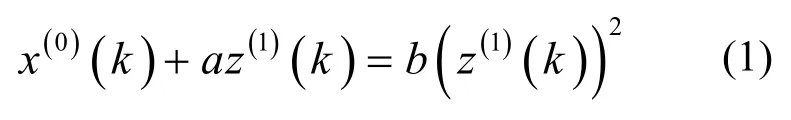
为灰色Verhulst模型。其对应的白化方程为

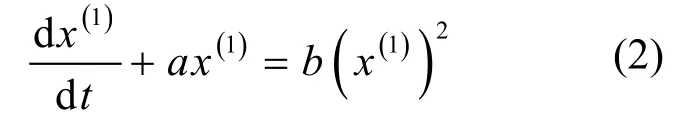
取 x(1)(1) = x(0)(1)，求解白化微分方程(2)得灰色Verhulst模型的时间响应式为

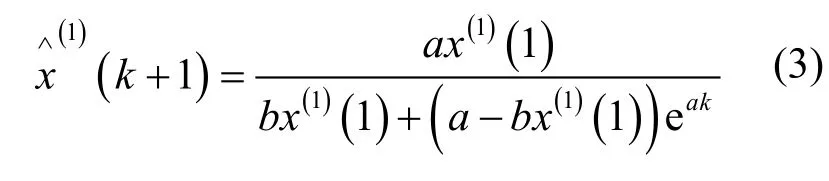
式中参数 a

∧

=(a ,b)T采用最小二乘估计为

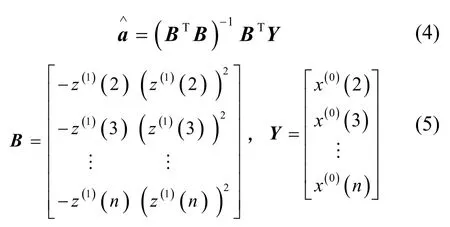
对式(3)进行一阶累减还原，得到原始负荷序列的预测值为

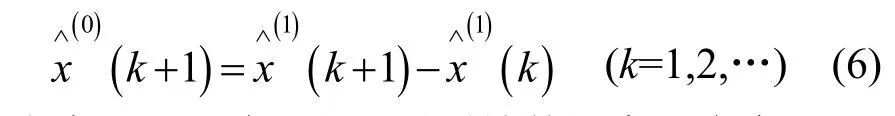
在实际问题中，当遇到原始数据序列本身呈“S型”时，通常的做法是取原始数据序列为 X(1)，其一阶累减序列为 X(0)，建立灰色Verhulst模型直接对X (1)进行模拟[17]。

2 灰色离散Verhulst模型

由第1节式(3)，对其作倒数变换，得到

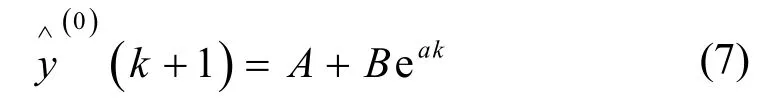
根据经典灰色Verhulst模型的建模过程可知，其参数估计采用离散形式的方程，模拟和预测采用连续形式的方程，从离散形式的估计到连续形式的预测这一过程本身就是一种近似，是一个跳跃，也是经典灰色Verhulst模型预测不准确的问题所在[16]。为了克服这一缺点，并结合式(7)所表现出来的性质，通过借鉴离散化思想，本文建立了离散灰色Verhulst模型。

由式(7)可知，原始负荷序列一阶累加生成序列的倒数变换序列呈现出非齐次指数增长规律，这就为构建非齐次指数的离散灰色模型提供了基础[16]。对 y(0)(k )进行一阶累加生成，得

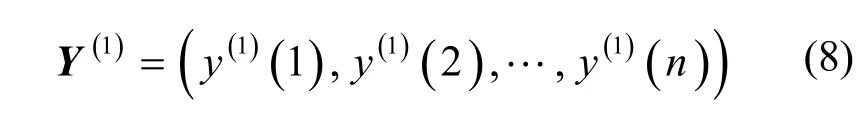
为灰色离散Verhulst模型。

值得说明的是，本文提出的模型与文献[15]提出的模型的最大区别是：后者是基于序列 y(0)(k)直接建立起如式(9)所示的灰色离散Verhulst模型，而本文则是先对 y(0)(k)进行一次累加生成而后建立起灰色离散Verhulst模型。

3 灰色离散Verhulst模型求解

对式(9)所示的灰色离散Verhulst模型中的带估计参数 β =(β ,β ,β)T，运用最小二乘法得参数

1 2 3估计为

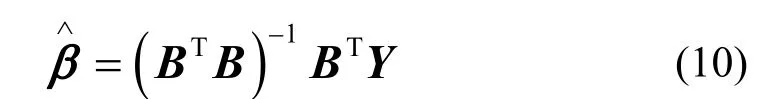
式中：

很显然，由灰色离散Verhulst模型的建模过程可知，从参数估计到预测表达式均为离散形式的方程，从而有效地避免了经典灰色Verhulst模型缺陷。

4 灰色离散Verhulst模型预测方法改进

灰色系统理论是利用系统实现的少数几个数据，通过数据生成变换建立起模型，其图解说明如图1所示[18]。

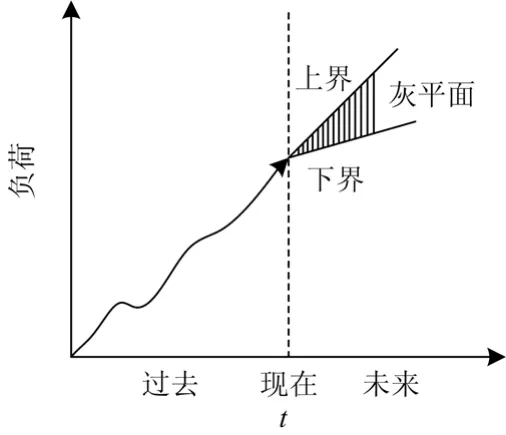
图 1 灰色理论的图解说明Fig. 1 Illustration of gray model

由图1可知，预测值上界和下界所夹部分称之为灰平面，它由原点（现在时刻）向未来时刻呈“喇叭型”展开，其大小由各个未来时刻预测值的灰区间决定。随着时间的推移，预测值灰区间会越来越大，这就决定了灰色预测的一个重要特点，即真正具有实际意义并且预测精度较高的预测值仅仅是整个预测序列中的第一、第二个预测值，而其他更远的预测值则只能反应未来发展的趋势[12]。

为了解决这个问题，文献[18]中列举了新息预测法、等维灰数递补预测法和等维新息预测法等三种方法。基于此，对于本文提出的灰色离散Verhulst模型采用等维灰数递补预测法。即由所得模型进行单步预测，将所得预测值补充到已知数列中，同时去掉最老的一个数据，保持序列维数不变，然后再根据新的已知数列建立模型，进行下一步预测，如此反复，依次递补，直到完成预测目标为止。

5 案例分析

为了说明本文提出的灰色离散Verhulst模型的有效性。本文采用文献[12]中陕西省某市1984~1990年用电量作为预测样本，对该市1996和1997年的用电量进行预测。数据如表1所示。

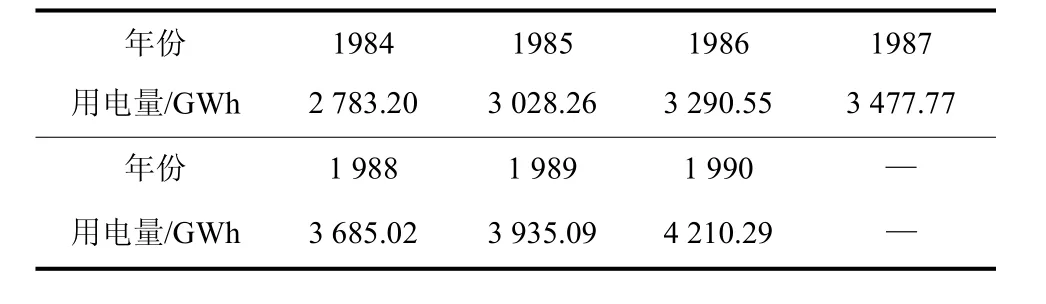
表1 陕西省某市1984~1990年用电量数据Table 1 Electric energy data of a certain city of Shaanxi province from 1984 to 1990

为了便于比较模型的优劣，在这里设经典灰色Verhulst模型为模型1，文献[12]中模型即经典灰色Verhulst模型的等维灰数递补预测模型为模型2，文献[15]所提出的灰色离散Verhulst模型为模型3、其等维灰数递补预测模型为模型4，本文提出的灰色离散Verhulst模型为模型5、其等维灰数递补预测模型为模型6。预测结果的优劣通过预测值相对误差ε来体现，其计算公式为

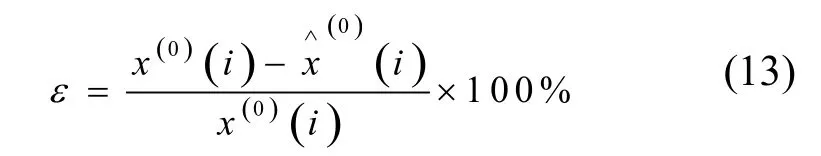
式中：x(0)(i)第i年负荷实际值；x∧

( 0

)(i )为第i年负荷预测值。

因为本文案例分析数据本身呈现出“S型”，按第1节所述在原始负荷数据的基础上直接建立起模型1，模型3和模型5。其所得参数估计分别为

其模型的响应式分别为

采用模型1~模型6预测1991~1997年的负荷电量值。由于受条件的限制，仅知道1996和1997年实际电量值，分别为6 078.16 GWh和6 364.68 GWh。各模型的预测结果如表2所示。

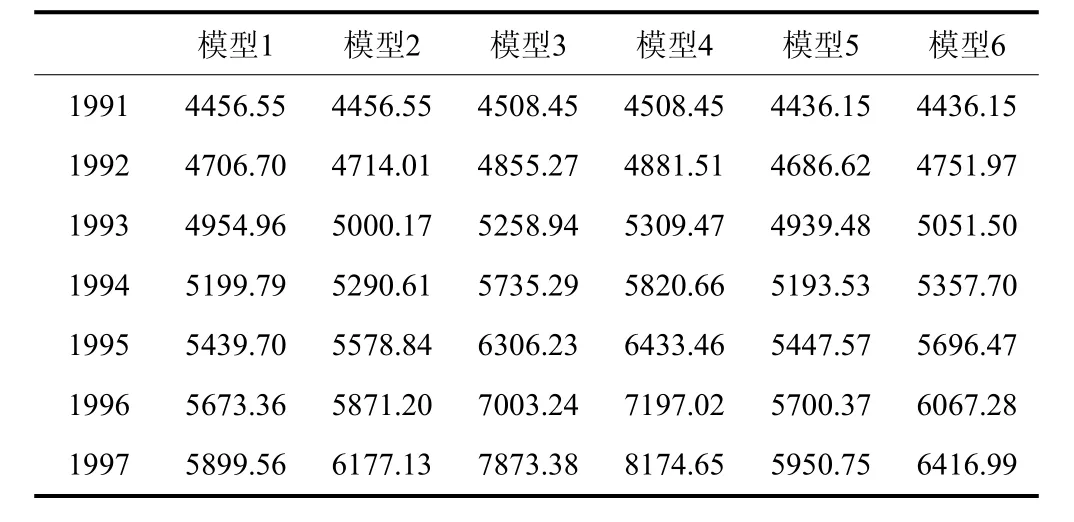
表 2 1991~1997年不同模型的预测结果Table 2 Forecasting results of different models from 1991 to 1997

根据1996所和1997年实际电量值以及各模型的预测值，由式(13)可计算得各模型预测结果的相对误差，如表3所示。

表 3 1996~1997年不同模型的预测相对误差Table 3 Forecasting relative errors of different models from 1996 to 1997%

由表2和表3的结果，比较模型1、3和5可知模型5使预测精度在一定程度上有所改观，但模型3则明显变差，其原因如下：

(1) 文献[15]中提出的模型3是基于原始数据序列一阶累加生成序列的倒数序列直接建立起灰色离散Verhulst模型，而序列 y(0)(k)实际上呈现出非齐次指数规律，其一阶累减还原序列呈现出齐次指数增长规律，直接用这种规律的序列建立形如非齐次指数的离散灰色模型的灰色离散Verhulst模型缺乏理论依据，因此会产生较大误差。

(2) 本文根据 y(0)(k)序列所呈现的规律，首先对 y(0)(k)序列进行一阶累加生成，而后建立灰色离散Verhulst模型，整个建模过程符合非齐次指数增长离散灰色模型的建模理论，所以能够在一定程度上提高预测精度。

比较模型2、4和6可知模型2和模型6都提高了预测精度，尤其是模型6使得预测精度得到大幅度提高，而模型4则变差，其原因是三种模型都采用等维灰数递补预测法，将预测值补充入原始序列，并剔除掉与目标相距最远的原始值，这符合新息优先原则[2]，理论上每种模型的预测精度都应该得到提高，但模型4由于其预测值即灰数灰度太大，灰度积累使得后面的预测值越来越不可信，故精度变差[18]。

综上所述本文提出的模型5和模型6符合建模理论，并且具有更好的预测精度。

6 结论

通过分析呈“S型”增长的负荷序列的一阶累加生成序列的倒数序列的特点，对最终的倒数序列进行一阶累加生成，在此基础上利用非齐次指数增长离散灰色模型的建模理论建立起了灰色离散Verhulst模型，并给出了该模型的递推解的形式。

借鉴灰色离散化理论建立起来的灰色离散Verhulst模型克服了经典灰色Verhulst模型由于参数估计采用离散形式的方程，模拟和预测采用连续形式的方程这一缺点所带的系统误差。从案例分析可以看出离散的参数估计到离散的预测模型更符合建模规律，具有更高的预测精度。

根据灰色预测理论的预测特点，采用等维灰数递补预测法对灰色离散Verhulst模型进行改进，克服了其随着时间的逐渐外推，预测逐渐失真的缺点，使得灰色预测模型对于后推若干年的预测仍然有效成为可能。

通过实例证明，本文提出的方法是正确的和有效的。

[1] 牛东晓, 曹树华, 卢建昌, 等. 电力负荷预测技术及其应用[M]. 2 版. 北京: 中国电力出版社, 2009.

[2] 康重庆, 夏清, 刘梅. 电力系统负荷预测[M]. 北京:中国电力出版社, 2007.

[3] 康重庆, 夏清, 张伯明. 电力系统负荷预测研究综述与发展方向的探讨[J]. 电力系统自动化, 2004, 28(17):1-11.KAN Chong-qing, XIA Qing, ZHANG Bo-ming. Review of power system load forecasting and its development[J].Automation of Electric Power Systems, 2004, 28(17):1-11.

[4] 毛李帆, 江岳春, 姚建刚, 等. 采用正交信号修正法与偏最小二乘回归的中长期负荷预测[J]. 中国电机工程学报, 2009, 29(16): 82-88.MAO Li-fan, JIANG Yue-chun, YAO Jian-gang, et al.Medium and long term load forecasting based on orthogonal signal correction and partial least-squares reggression[J]. Proceedings of the CSEE, 2009, 29(16):82-88.

[5] 黎灿兵, 杨朋, 刘玮, 等. 短期负荷预测中考虑夏季气温累积效应的方法[J]. 电力系统自动化, 2009, 33(9):96-99.LI Can-bing, YANG Peng, LIU Wei, et al. An analysis of accumulation effect of temperature in short-term load forecasting[J]. Automation of Electric Power Systems,2009, 33(9): 96-99.

[6] 周平, 杨岚, 周家启. 电力系统负荷灰色预测的新方法[J]. 电力系统及其自动化学报, 1998, 10(3): 45-50.ZHOU Ping, YANG Lan, ZHOU Jia-qi. The new method of electric power system load gray forcast[J].Proceedings of the CSU-EPSA, 1998, 10(3): 45-50.

[7] 张红旭, 姚建刚, 曹伟, 等. 基于改进灰色模型的超短期负荷预测[J]. 电力系统及其自动化学报, 2009, 21(6):74-77.ZHANG Hong-xu, YAO Jian-gang, CAO Wei, et al.Ultra-short term load forecasting based on improved gray model[J]. Proceedings of the CSU-EPSA, 2009, 21(6):74-77.

[8] 王捷, 吴国忠, 李艳昌. 蚁群灰色神经网络组合模型在电力负荷预测中的应用[J]. 电力系统保护与控制,2009, 37(2): 48-52.WANG Jie, WU Guo-zhong, LI Yan-chang. Application of ant colony gray neural network combined forecasting model in load forecasting[J]. Power System Protection and Control, 2009, 37(2): 48-52.

[9] 周德强. 基于最小一乘法的 GM(1,1)模型及在负荷预测中的应用[J]. 电力系统保护与控制, 2011, 39(1):100-103.ZHOU De-qiang. GM(1,1) model based on least absolute deviation and its application in the power load forecasting[J]. Power System Protection and Control,2011, 39(1): 100-103.

[10] 周德强, 武本令. 灰色BP神经网络模型的优化及负荷预测[J]. 电力系统保护与控制, 2011, 39(21): 65-69.ZHOU De-qiang, WU Ben-ling. Optimization and power load forecasting of gray BP neural network model[J].Power System Protection and Control, 2011, 39(21):65-69.

[11] 王成山, 杨军, 张崇见. 灰色系统理论在城市年用电量预测中的应用[J]. 电网技术, 1999, 23(2): 15-18.WANG Cheng-shan, YANG Jun, ZHANG Chong-jian.Application of grey system theory in city electricity demand forecasting[J]. Power System Technology, 1999,23(2): 15-18.

[12] 张伏生, 刘芳, 赵文彬, 等. 灰色 Verhulst模型在中长期负荷预测中的应用[J]. 电网技术, 2003, 27(5): 37-40.ZHANG Fu-sheng, LIU Fang, ZHAO Wen-bin, et al.Application of grey Verhulst model in middle and long term load forecasting[J]. Power System Technology, 2003,27(5): 37-40.

[13] 周德强. 改进的灰色 Verhulst模型在中长期负荷预测中的应用[J]. 电网技术, 2009, 33(18): 124-127.ZHOU De-qiang. Application of improved gray Verhulst model in middle and long term load forecasting[J]. Power System Technology, 2009, 33(18): 124-127.

[14] 王正新, 党耀国, 刘思峰. 无偏灰色Verhulst模型及其应用[J]. 系统工程理论与实践, 2009, 29(10): 138-144.WANG Zheng-xin, DANG Yao-guo, LIU Si-feng.Unbiased grey verhulst model and its application[J].Systems Engineering-Theory ＆amp; Practice, 2009, 29(10):138-144.

[15] 崔立志, 刘思峰, 李致平. 灰色离散 Verhulst模型[J].系统工程与电子技术, 2011, 33(3): 590-593.CUI Li-zhi, LIU Si-feng, LI Zhi-ping. Grey discrete verhulst model[J]. Systems Engineering and Electronics,2011, 33(3): 590-593.

[16] 谢乃明. 灰色系统建模技术研究[D]. 南京: 南京航空航天大学, 2008.

[17] 刘思峰, 党耀国, 方志耕, 等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2004.

[18] 傅立. 灰色系统理论及其应用[M]. 北京: 科学技术文献出版社, 1992.