针对独立风光发电中混合储能容量优化配置研究

杨 珺 ，张建成，周 阳，牛 虎，梁廷婷

（1.新能源电力系统国家重点实验室（华北电力大学），河北 保定 071003；2.国网新源张家口风光储示范电站有限公司，河北 张家口 075000）

0 引言

为了保护环境和人类的可持续发展，各种可再生能源的利用和研究已经日益受到人类的重视。目前众多可再生能源技术开发中，潜力最大、发展应用前景最好的是风能和太阳能。它们作为可再生的能源具有分布广泛、再生、无污染等优点，近年来得到了快速的发展[1-2]。风光发电系统是可再生能源发电系统的一种重要形式，其相对于风力发电或光伏发电具有更平稳的电力输出能力和更高的可靠性，同时还能降低对储能的要求[3]。

目前，风光发电系统和光伏发电系统中常用的储能装置是铅酸蓄电池[4-5]。蓄电池的比能量高，便于长期存储电能，能使整个风光发电系统的能量调节范围增加。但它循环寿命短、功率密度低、环境污染严重，加之风光发电系统输出功率的不稳定性和间歇性，往往导致蓄电池过早失效或容量损失，加大了系统成本，限制风光发电系统的大规模快速发展。超级电容器作为一种新型的储能器件，具有功率密度大、充放电速度快、循环寿命长等无可替代的优良特性，可以有效抑制系统的短时功率波动，成为处理尖峰负荷的最佳选择。有关研究也表明，将蓄电池和超级电容器同时作为储能装置能够使蓄电池工作在优化的充放电状态，显著减少蓄电池充放电次数，延长其使用寿命[5]，从而大大降低系统运行成本。

目前，国内外已经开展了对风光发电系统储能容量优化配置的研究[6-7]，但这些研究基本上仅考虑单一储能装置的容量优化，仍不能有效的降低储能成本。本文将超级电容器和蓄电池混合共同作为独立风光发电系统的储能装置，对独立风光发电中储能容量优化配置展开研究。

1 模型分析

1.1 风光发电系统结构与原理

基于蓄电池/超级电容器混合储能的独立风光发电系统主要由风力发电机、光伏阵列、储能系统、逆变器、负载等部分组成，其结构简图如图1所示。

图1 基于混合储能的独立风光发电系统结构图Fig. 1 Structure of independent Wind/PV system based on hybrid storage system

在风光资源充足时，储能装置处于充电状态，将多余的电能存储起来，提高风光资源利用率；在风光资源不足或遇峰值负荷时储能装置释放储存的电能供给负荷，以保证系统平稳连续的供电；当遇到长期阴雨天气且风力较弱时，风光电源无法正常发电，储能系统仍能够满足重要负荷一定时间内的用电要求，提高系统的供电可靠性。

1.2 储能装置模型

现建立蓄电池和超级电容器的数学模型，为下一节储能系统容量优化研究奠定基础。

a. 蓄电池组模型

记单体蓄电池的标称额定容量为baC (Ah)，额定电压为baU (V)，则对于级联数量为m的蓄电池组，其储能总量banE（单位MWh⋅，本节统一能量单位MWh⋅，功率单位MW）为

假设给定蓄电池的最大放电深度为DOD，则该蓄电池组最小的剩余能量

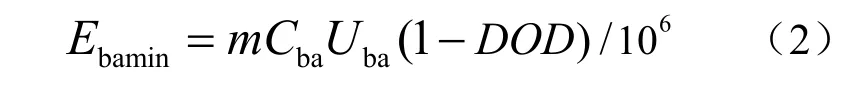
通常情况下，蓄电池以C10的时间率放电，则上述蓄电池组的额定输出功率为

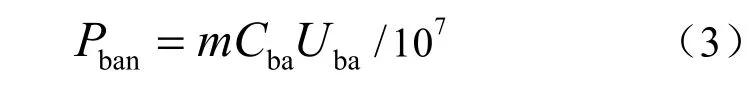
b. 超级电容器组模型

假设超级电容器的电容值为 Cuc，端电压为Uuc，则对于级联数量为n的超级电容器储存的能量公式为

在实际的应用中，超级电容器的端电压会有一个工作范围，记为：Uucmin~ Uucmax，则该超级电容器组存储能量的上下限分别为

2

9

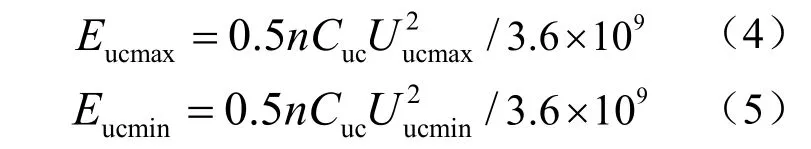
记单体超级电容器最大工作电流为ucmaxI ，则级联数量为n的超级电容器组的最大输出功率可表示为

由于电源输出功率 Ps和负荷功率 Pl均具有很强的随机波动性，因此储能装置的储能量也在随时间相应地不断变化。

当 Ps( kt)ηc＆gt; Pl(kt )时储能装置处于充电状态，储能装置的储能量可以表示为

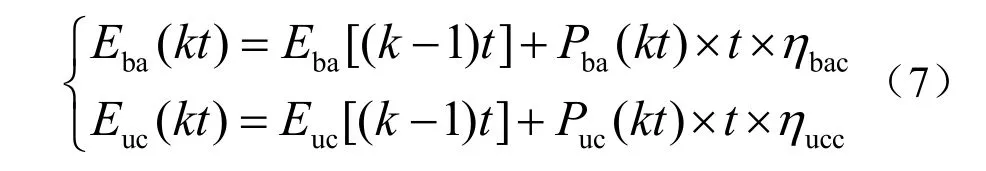
当 Ps( kt)ηc＆lt; Pl(kt )时储能装置处于放电状态，储能装置的储能量可以表示为

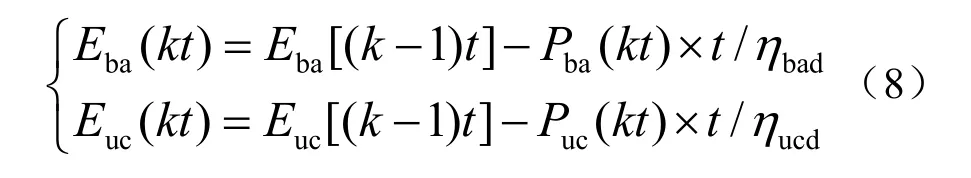
式中：ηc是系统逆变器的功率转换效率；Eba(kt)，Euc(k t)分别为蓄电池组和超级电容器组kt时刻的储能量； Eba[(k −1)t]，Euc[(k−1)t]分别为蓄电池组和超级电容器组(k−1)t时刻的储能量；Pba(kt)，Puc(kt)分别为蓄电池组和超级电容器组在kt时刻的充放电功率；ηbac，ηbad，ηucc，ηucd分别为蓄电池组和超级电容器组充放电效率。

2 混合储能系统能量管理策略

2.1 能量管理策略

考虑到间歇式电源功率的波动性，并结合蓄电池和超级电容器互补的储能特性，提出适合该混合储能系统的能量管理策略如下：为充分发挥超级电容器功率密度大，循环寿命长，响应速度快的优势，同时有效回避其能量密度低的缺陷，超级电容器主要承担不平衡功率dp中的频繁波动功率；蓄电池只负责承担不平衡功率dp中的基本功率，这样可以有效避免蓄电池频繁充放电造成的小循环充放电现象，且蓄电池均以额定功率充放电，保证蓄电池处于优化的工作状态，延长蓄电池的使用寿命，提高储能系统整体的经济性。

2.2 LPSP计算流程

所谓负荷的缺电率(Loss of Power Supply Probability，LPSP)就是在系统运行过程中，负荷缺电量(LPS)与负荷总需求量的比值，满足下式[8]

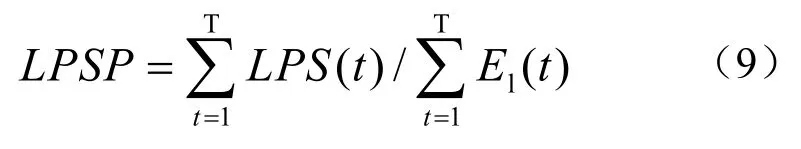
其中：t为单位时间间隔；T为总计算次数。

针对上述能量管理策略，分析该风光发电系统的 LPSP计算流程如图 2。当风光电源功率足以满足负荷要求，即时，负荷缺电量(LPS)为零，储能装置充电，具体过程见图3；当风光电源功率不足，即时，储能装置放电弥补电源功率缺额，负荷缺电量(LPS)的计算示于图4。

图2 LPSP计算流程图Fig. 2 Flowchart of Loss of Power Supply Probability

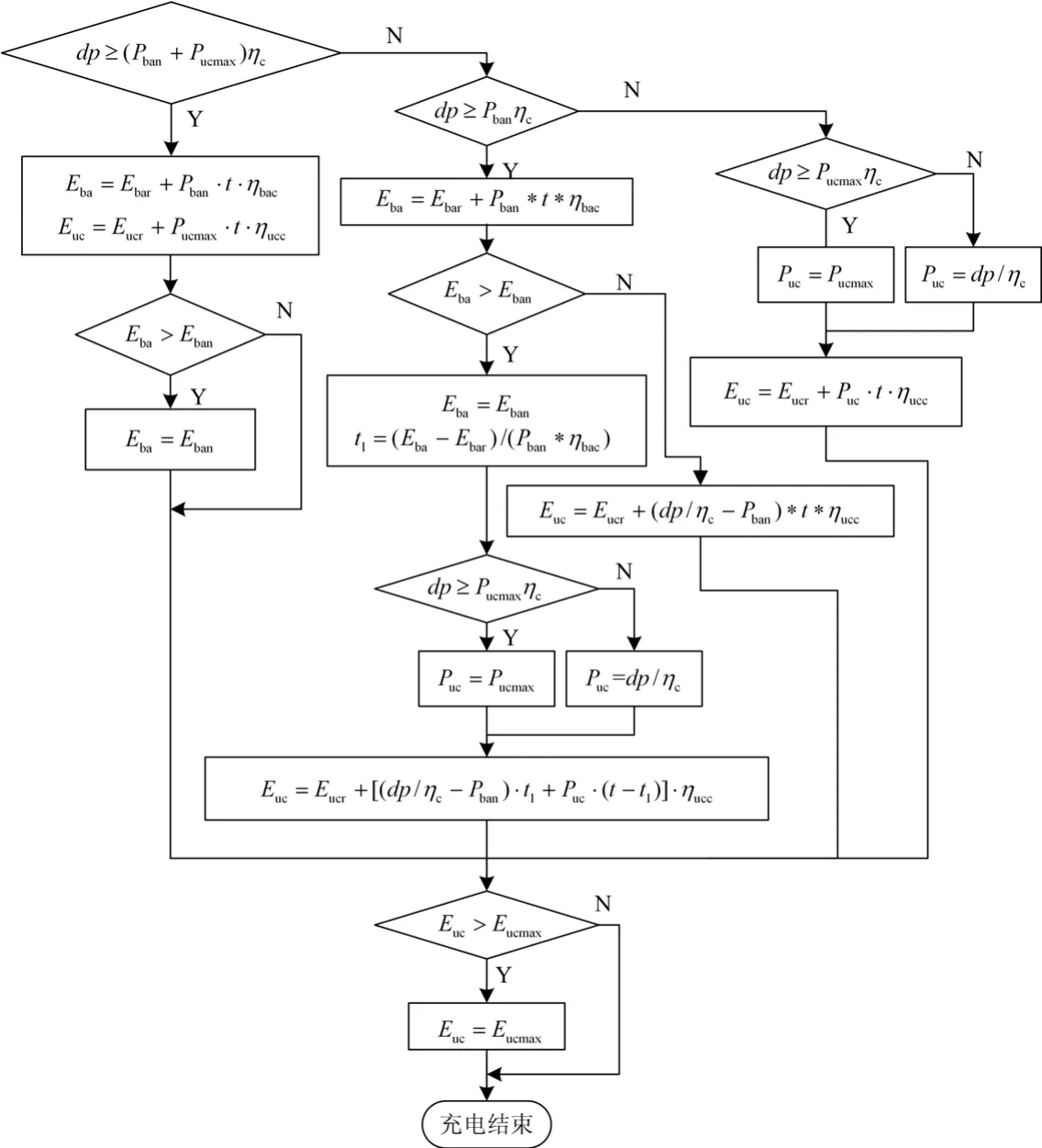
图3 储能装置充电时LPSP的计算流程图Fig. 3 Flowchart of Loss of Power Supply Probability when energy storing device is charging

图4 储能装置放电时LPSP的计算流程图Fig. 4 Flowchart of Loss of Power Supply Probability when energy storing device is discharging

3 储能系统容量优化模型

3.1 优化目标函数

根据IEC60300-3-3（国际电工委员会制定的全寿命周期成本计算的标准）的规定[9]，设备的全寿命周期成本（Life Cycle Cost，LCC）是指整个寿命周期内所消耗的总成本，包括购置成本(Acquisition Cost)，拥有成本(Ownership Cost)和废弃成本(Disposal Cost)。

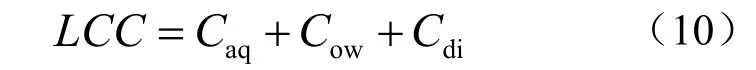
其中：LCC是全寿命周期成本； Caq是设备的购置成本； Cow是设备的拥有成本（运行和维护成本）；Cdi是设备的废弃成本（报废成本和残值）。

对LCC模型的主要构成要素进行具体的分析，将储能系统优化目标模型定义为四大成本之和，即IEC标准中的购置成本、运行成本、维护成本以及处置成本，并给出具体的表达式[10]

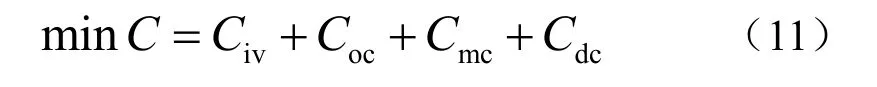
其中：ivC 指储能装置的购置成本（investment cost），包括储能装置及其附加设备的购置成本；ocC 指储能装置的运行成本（operating cost），包括储能装置的试验、安装、损耗、停运成本、人工费用等；mcC指储能装置的维护成本（maintenance cost），包括故障前的检修成本和故障后的维修成本；dcC 指储能装置的处置成本（disposal cost），包括储能装置的报废成本和残值。

上述优化目标模型克服了传统经济性优化问题中只注重降低初始购置成本的局限性，将储能装置成本延伸到安装、运行、维护、失效报废等整个寿命期过程中使得优化结果更符合实际情况，更具有现实意义。

3.2 优化约束条件

根据上述能量管理策略，并考虑独立风光发电系统的运行特性，研究适用于独立风光发电系统的储能系统容量优化配置的约束条件如式（12）

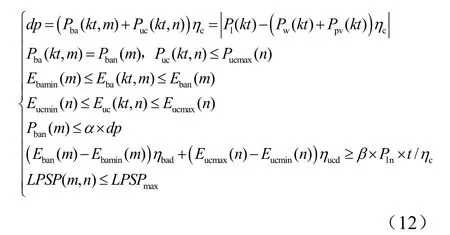
式中：m，n表示蓄电池组和超级电容器组的个数；α表示不平衡功率dp中基本功率所占比例；β是额定负荷lnP中重要负荷的比例系数。

第一个公式属于系统合理性的要求；第二、三、四个公式是保证蓄电池和超级电容器正常运行的基本约束，可以看出为延长蓄电池寿命，蓄电池功率值设定为其额定功率；第五个公式体现了所提的能量管理策略，即蓄电池的功率输出维持在基本负荷以内；第六个公式表示用户对独立风光发电系统自主能力的要求，即当遇到连续阴雨且无风天气时，风机与光伏电源无法正常发电，储能系统仍能够保证重要负荷不间断供电小时数；第七个公式是指独立风光发电系统需要满足一定的供电可靠性，这里以负荷缺电率（LPSP）作为供电可靠性指标。

4 算例分析

以某国家示范工程一期建设项目为例进行分析计算，该建设项目包含100 MW的风电系统和40 MW 的太阳能光伏发电系统，假设当地负荷为 80 MW，且独立运行，现在为其配置储能容量。详细参数如表1。

本文采取50个蓄电池单体、100个超级电容器单体串并联分别组成蓄电池组和超级电容器组，根据图5所示，风电年发电预测数据、光伏年发电预测数据、负荷年用电预测数据，运用改进粒子群优化算法[11-12]对优化问题进行求解。

当采用基本能量管理策略进行优化计算时，即不考虑对蓄电池的工作状态进行优化，蓄电池和超级电容器工作不分优先次序，平等的弥补不平衡负荷，优化计算结果如表2所示。

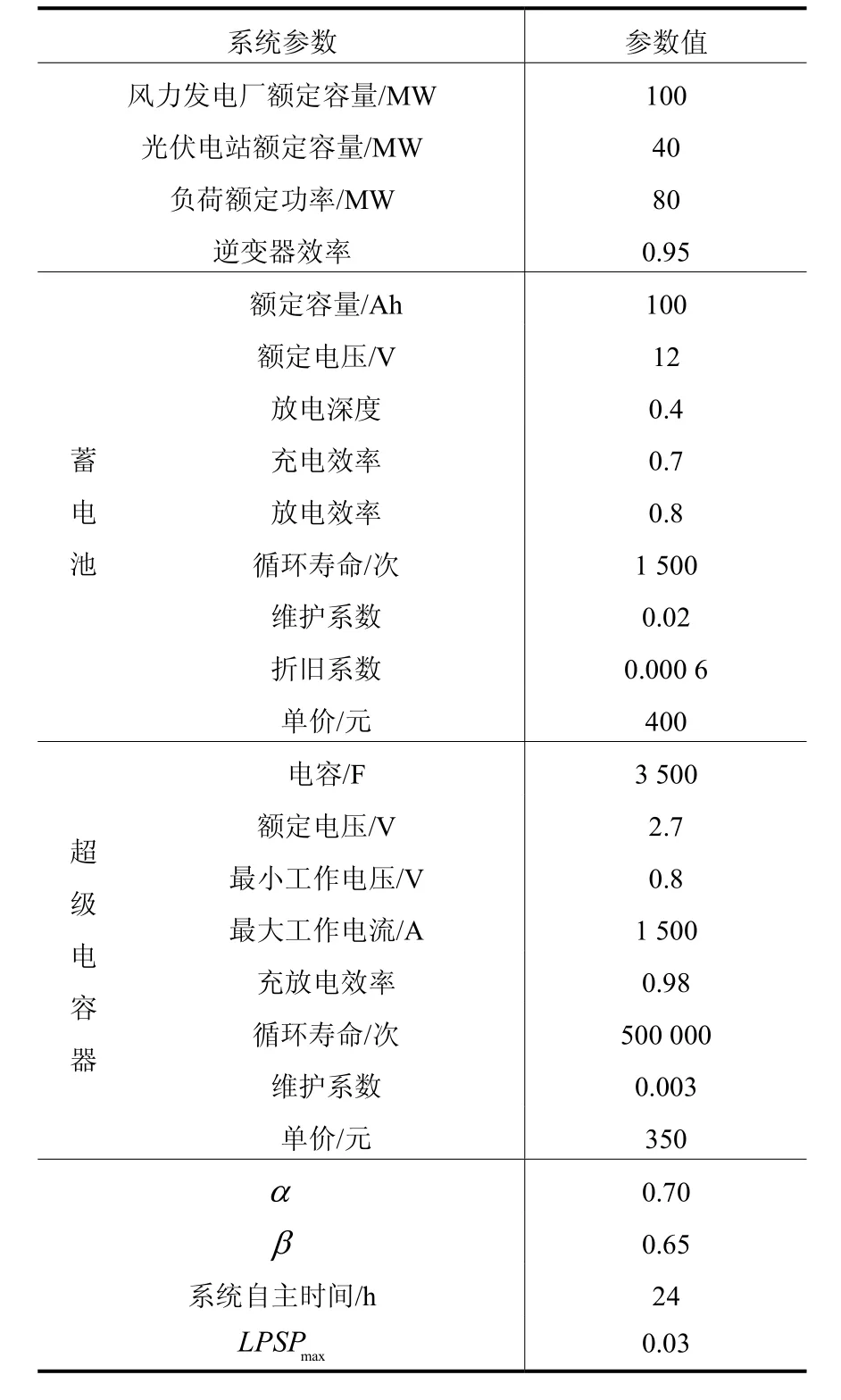
表1 系统参数Table 1 System parameters

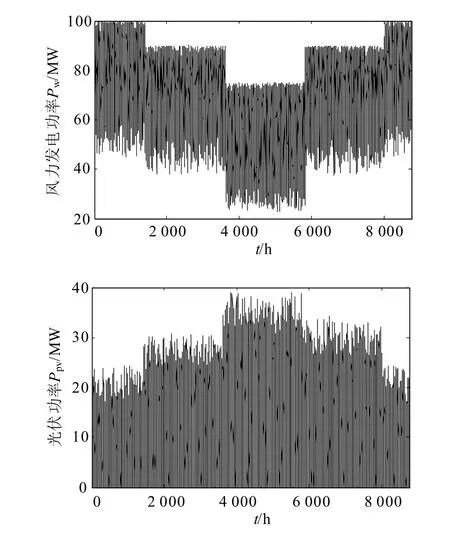
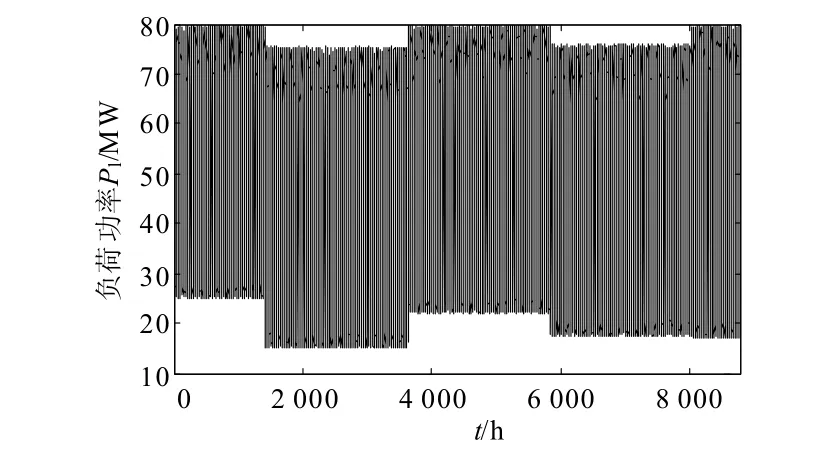
图5 风电功率/光伏发电功率/负荷功率0.5 h发电预测值Fig. 5 Forecast of half an hour of wind power / photovoltaic power / load power

表2 基本能量管理策略优化计算结果Table 2 Optimization results of basic energy management strategy

采用本文所提能量管理策略进行优化计算，优化计算结果如表3所示。

表3 新能量管理策略优化计算结果Table 3 Optimization results of new energy management strategy

通过表2和表3的数据可以看出，在相同的供电可靠性约束下，本文所提能量管理策略比基本策略计算所得年平均最小费用要少近20万，同时可以发现蓄电池的折旧程度相差两倍多，因此本文所提能量管理策略可以使整个储能系统的运行年限延长，这就在相当程度上节省了储能开支。由此得出新的能源管理策略能够更加充分地发挥两种储能元件的互补优势，有效降低储能系统成本。

根据表3优化结果数据，绘制蓄电池组和超级电容器组在一年中4300 h~4400 h时间段的输出功率变化曲线如图6所示，其中Pba表示蓄电池输出功率，Puc表示超级电容器输出功率。

由图6可以看出，由于超级电容器组的参与，蓄电池组的输出功率变化很平坦，峰值不平衡功率和频变不平衡功率主要由超级电容器组提供，这样可以有效地优化了蓄电池组的工作状态，延长了其使用寿命，最终减少了储能系统的运行维护等费用。

图6 超级电容器组/蓄电池组输出功率曲线Fig. 6 Power curves of ultracapacitor pile / storage battery pile

5 结论

本文通过分析超级电容器和蓄电池的储能特性，建立了其数学模型；根据风光电站功率输出特性以及负荷功率波动特性，充分利用超级电容器和蓄电池优良的互补性，提出了适合该类混合储能系统的能量管理策略，并分析了此能量管理策略下的系统负荷缺电率（LPSP）的计算流程；建立以全生命周期费用（LCC）理论为基础的储能容量优化目标函数，以独立风光发电系统负荷缺电率（LPSP）等可靠性指标为约束条件的优化模型，运用改进粒子群算法进行优化问题的求解。最后通过算例验证了所提能量管理策略能够更加充分地发挥两种储能元件的互补优势，有效降低储能系统成本。本文所提出的容量优化方法与策略为风光发电系统独立运行时储能系统的配置提供了方法，对于联网运行系统容量优化设计方法同样具有参考意义。

[1] 冬雷, 廖晓钟, 刘广忱, 等. 分布式风光互补发电系统及其多目标优化控制策略研究[J]. 仪器仪表学报,2005, 26(8): 750-753.DONG Lei, LIAO Xiao-zhong, LIU Guang-chen, et al.Multi-index optimization control strategy based on distributed PV and wind energy complemental generation system[J]. Chinese Journal of Scientific Instrument, 2005,26(8): 750-753.

[2] 刘立群, 王志新, 顾临峰. 基于改进模糊法的分布式风光互补发电系统MPPT控制[J]. 电力系统保护与控制, 2011, 39(15): 70-74 , 79 .LIU Li-qun, WANG Zhi-xin, GU Lin-feng. MPPT control based on improved fuzzy method for distributed hybrid wind-solar power[J]. Power System Protection and Control, 2011, 39(15): 70-74, 79.

[3] 徐大明, 康龙云, 曹秉刚. 风光互补独立发电系统的优化设计[J]. 太阳能学报, 2006, 27(9): 919-922.XU Da-ming, KANG Long-yun, CAO Bing-gang.Optimal design of standalone hybrid Wind/PV power systems[J]. Acta Energiae Solaris Sinica, 2006, 27(9):919-922 .

[4] 李少林, 姚国兴. 风光互补发电蓄电池超级电容器混合储能研究[J]. 电力电子技术, 2010, 44(2): 12-14.LI Shao-lin, YAO Guo-xing, Research on ultracapacitor /battery energy storage in Wind/Solar power system[J].Power Electronics, 2010, 44(2): 12-14.

[5] 周林, 黄勇, 郭珂, 等. 微电网储能技术研究综述[J].电力系统保护与控制, 2011, 39(7): 147-152.ZHOU Lin, HUANG Yong, GUO Ke, et al. A survey of energy storage technology for micro grid[J]. Power System Protection and Control, 2011, 39(7): 147-152.

[6] Zhao Y S, Zhan J, Zhang Y, et al. The optimal capacity configuration of an independent Wind/PV hybrid power supply system based on improved PSO algorithm[C] //Advances in Power System Control, Operation and Management (APSCOM 2009), 8th International Conference on, 2009: 1-7.

[7] Fatemeh Jahanbani Ardakani, Gholamhossein Riahy,Mehrdad Abedi. Design of an optimum hybrid renewable energy system considering reliability indices[C] //Electrical Engineering (ICEE), 2010 18th Iranian Conference on, 2010: 842-847.

[8] Testa A, de Caro S, La Torre R, et al. Optimal design of energy storage systems for stand-alone hybrid Wind/PV generators[C] // Power Electronics Electrical Drives Automation and Motion (SPEEDAM), 2010 International Symposium on, 2010: 1291-1296.

[9] International Electrotechnical Commission. Life cycle costing[S]. International Standard 60300-3-3, 2004.

[10] 崔新奇, 尹来宾, 范春菊, 等. 变电站改造中变压器全生命周期费用(LCC)模型的研究[J]. 电力系统保护与控制, 2010, 38(7): 69-73.CUI Xin-qi, YIN Lai-bin, FAN Chun-ju, et al. Study of LCC for power transformer in modification of transformer substation[J]. Power System Protection and Control, 2010, 38(7): 69-73.

[11] 黄友锐. 智能优化算法及其应用[M]. 北京: 国防工业出版社, 2008.HUANG You-rui. Intelligent optimization algorithms and its application[M]. Beijing: National Defense Industry Press, 2008.

[12] 姜文, 严正. 基于一种改进粒子群算法的含风电场电力系统动态经济调度[J]. 电力系统保护与控制, 2010,38(21): 173-178, 183.JIANG Wen, YAN Zheng. Dynamic economic dispatch considering wind power penetration based on IPSO [J].Power System Protection and Control, 2010, 38(21):173-178, 183.