地波雷达目标方位角估计算法

卢庆广，梁艳红，周东瑜

(海军工程大学海洋电磁环境研究所，湖北武汉430033)

地波雷达目标方位角估计算法

卢庆广，梁艳红，周东瑜

(海军工程大学海洋电磁环境研究所，湖北武汉430033)

地波雷达由于其良好的超视距目标探测性能得到广泛重视与研究。而作为参数估计的重要组成部分，获取精确的目标方位估计算法一直是地波雷达阵列信号处理的主要工作。近年来，地波雷达阵列天线不断趋向于小型化，使得在进行方位角估计过程中，高分辨算法得到了研究与应用。本文针对地波雷达阵列接收信号数据特点，重点对比分析3种高分辨算法的性能，为DOA估计提供算法选择依据，具有重要的工程应用价值。

地波雷达;方位估计;高分辨算法

0 引言

地波雷达(HFSWR)又称表面波雷达，工作在高频波段(频率一般为3～30 MHz)，波长较长，工作在目标谐振区，具有很好的超视距探测性能。但由于其工作在高频段，电磁环境恶劣［1］，工作频带常常受限。为保证系统较高的信噪比与良好的角度分辨力，一般需要使用大型接收阵列天线，而在工程实践中，阵列的大小又受到限制，使小型化阵列天线备受亲睐。然而，小型化阵列孔径宽度有限，常规波束形成方法经常造成目标不能正确分辨，测角误差较大，因此大量的高分辨算法 (超过瑞利限的方法)应运而生，实现了与大型化天线阵相当的角度分辨力［2］，其中以MUSIC算法最为经典。

目标到达方向 (DOA)估计问题是地波雷达阵列信号处理中的一个基本问题，也是宽波束雷达信号处理的难点。本文针对几种经典高分辨DOA估计方法进行深入研究，根据地波雷达数据特点，对比分析几种算法各自的优缺点，从而为选择合理的DOA估计方法，提高地波雷达测角精度提供重要依据。

1 阵列信号模型

地波雷达常用接收天线阵列有线阵、平面阵、圆阵和不规则阵列等。其中均匀线阵(ULA)最具有代表性，为简单起见，假设接收阵列为间距为d的N元均匀线列阵。假定ULA位于x轴上，考虑阵列接收为窄带信号，为平面波入射，波长为λ，由于地波雷达电磁波沿海面传播，这里只考虑水平方位角θi，单个信号入射如图1所示。

图1 N元ULA平面波入射Fig.1 N element ULA with incident uniform beam

阵列θi方向响应向量为

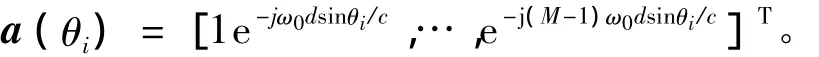
上标T表示转置，由L个方向上入射信号得到阵列输出端的测量模型为

其中，矩阵 A(θ)=［a(θ1)a(θ2)…a(θl)］为由 L 个响应向量构成的矩阵，也称作阵列的阵列流形;s(t)为接收到信号的复包络;n(t)为阵列上的附加噪声向量，阵列接收端噪声可通过文献［3］中的预白化处理，使各个通道的输出噪声为相互独立的零均值高斯白噪声。

2 三种高分辨DOA估计方法

2.1 Capon最小方差法

Capon算法［4］(也称为最小方差法MVM)能够提供远高于常规波束形成法(CBF)的分辨能力，其求解的目标函数为

式中R=E［x(t)xH(t)］为阵列输出协方差矩阵。Capon算法试图使期望方向信源功率不变的同时，尽量消除期望以外方位的任何干扰所贡献的功率最小。通过使用标准Lagrange乘子法求解式(2)可得，最优加权矢量为

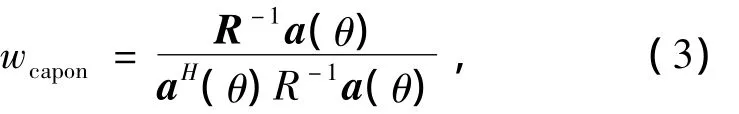
从而得到空间谱为

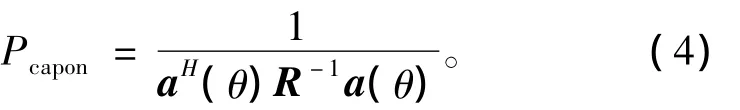
式中a(θ)为阵列扫描向量。目标DOA估计由式(4)最大值点给出。可见Capon算法仍然是直接通过利用采样数据的阵列输出协方差矩阵R进行DOA估计。

2.2 MUSIC多重信号特征法

基于特征分解的MUSIC法［5］具有普遍的适用性，其主要思想是通过对采样协方差矩阵进行特征分析，将其划为信号子空间和噪声子空间，即阵列协方差矩阵可用特征值和特征向量表示为

假设阵列上接收到的L个信号两两互不相干，且各个阵元上噪声相互独立且功率相等，由矩阵理论可知信号子空间与噪声子空间正交，也即阵列流形向量与噪声子空间的各个向量正交，可知

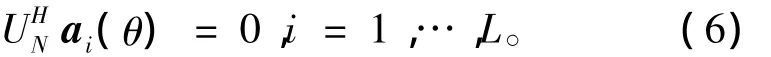
因此，可定义MUSIC的阵列空间谱函数为

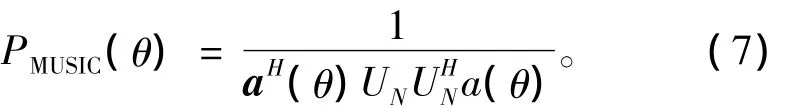
在实际应用中，通过改变扫描向量a(θ)，寻找式(7)的谱峰值来确定信号的方位角。

2.3 ES-DOA算法

ES-DOA算法［6］为基于特征空间的DOA估计算法，通过对接收信号的协方差矩阵进行重构，即

其中：I为N×N维单位矩阵的反转矩阵。将RX进行特征值分解后得到重构后的信号子空间和噪声子空间，得到一个新的空间谱函数为

3 仿真与性能分析

3.1 仿真数据与结果

根据第2节的阵列模型，假设接收天线阵为16元各向同性线阵，阵元间距为λ/2，阵元间不存在耦合，各通道幅相特性完全一致，以阵中心点为坐标原点，接收信号范围为［－90°，90°］，信源数为4，方位为［－10，0，10，20］，功率分别为［0.9，0.8，1，0.5］，且处在同一个距离多普勒单元中，各通道噪声与信号相互独立且信噪比为10 dB。

图2(a)中，快拍数为65，信号间相互独立，可以看到相同信噪比下，Capon，MUSIC和ES－DOA都能够较好地对准DOA方向，而谱峰依次更加尖锐，旁瓣也依次降低，可见估计性能依次升高。

图2(b)中，快拍数为9，信号间相互独立，可以看到在低快拍数情况下Capon算法估计明显发生误判，MUSIC算法估计谱峰不如ES－DOA尖锐，且其谱峰基底较图2(a)中明显上升，旁瓣升高。

图2(c)中，快拍数为65，信源1和信源3相干，并均与信源2和信号源4独立。可以看到，Capon和MUSIC算法估计在－10°，10°处均没有产生明显的谱峰，会发生误判，而ES－DOA算法依旧性能良好。

图2(d)中，快拍数为65，信号间相互独立，阵元数减少为10。可以看到，Capon算法在－10°，10°处均没有产生明显的谱峰，会发生误判，MUSIC算法估计谱峰不如ES－DOA尖锐。

图2(e)中，快拍数为65，信号间相互独立，阵元数仍为16，估计信源数为3。可以看到，MUSIC算法和ES－DOA算法发生了误判，而Capon算法虽然谱峰没有其他2种算法尖锐，但估计正确。

3.2 性能分析

通过仿真对比得到表1。

表1 空间谱估计效果对比表Tab.1 The contrast table of normalized spatial spectrum

表1中，差表示不能正确估计，中为能够较好估计，优为能很好估计。

因此，对表1进行分析得到以下结论：

1)随着快拍数的增加3种算法的信源估计性能都会更好，而Capon算法对快拍数最为敏感，低快拍数不能有效地进行信源DOA估计，MUSIC算法次之，ES-DOA算法最优。

图2 归一化空间谱Fig.2 Normalized spatial spectrum

2)在有相关信源存在的情况下，Capon算法和MUSIC算法非常敏感，不能有效地进行信源DOA估计，而ES-DOA算法最优。

3)在阵元数较少的情况下，MUSIC算法和ESDOA算法有较好分辨力，能够正确估计目标，Capon算法则效果非常不理想。

4)当信源数估计有误时，Capon算法性能表现良好，而MUSIC算法和ES-DOA算法非常敏感，不能有效估计目标方位。

对3种算法的空间谱公式分析可以看到，Capon算法直接利用了阵列接收信号协方差矩阵信息，仍属于常规技术;MUSIC算法只利用了噪声子空间信息，提高了估计性能;而ES-DOA通过对阵列协方差矩阵进行重构，得到RX为Toeplitz矩阵，使得在充分利用信号子空间和噪声子空间信息的同时具有很好的相干信源DOA估计能力;且后两者都属于超分辨算法。3种算法运算量相当且各有利弊，数据决定方法，因此需要对数据特点进行具体分析而后进行算法的优化选择。以成熟的FMICW波形地波雷达为例，由于宽波束和高多普勒分辨性质，需要进行长时间积累，快拍数因此也比较小，为了构造样本矩阵，一般通过多普勒维的滑窗获得足够的快拍数，但快拍数仍然有限，且造成样本具有很强的相关性;在使用信息论等方法做信源数估计时常常有误;同时，天线阵趋于小型化，阵元数较少，且由于地波雷达工作的电磁环境复杂，入射到阵列的信号很可能有相干信源存在。因此，综上可知，3种算法中ES－DOA算法相对于工程中较常使用的MUSIC算法有更强的适用性，不失为一种更好的选择。

4 结语

本文针对地波雷达DOA估计的数据特点，通过仿真，分别比较了3种算法在低快拍数、信号源相干、阵元数较少、信源数估计有误情况下的估计性能。分析表明，ES－DOA算法性能最优，MUSIC算法次之，Capon算法较差。为选择地波雷达DOA估计方法提供了重要依据，具有重要的工程实践价值。随着技术的发展，新的DOA估计方法层出不穷，在处理方法上有了更多的选择，如神经网络法［7］和时频分析法［8］等，需要进一步的研究创新，具体问题具体分析，以得到更好的效费比。

［1］FABRIZIO G A，GERSHMAN A B，TURLEY M D．Robust adaptive beam forming for HF surface wave over－thehorizon radar［J］．IEEE Trans．on Aerospace and Electronic Systems，2004，40(2)：510 －525．

［2］杨绍麟．高频海洋遥感雷达的天线阵设计与空间超分辨率算法［D］．武汉：武汉大学电子信息学院，2001．

［3］XIE J H，YUAN Y S，LIU Y T．Super-resolution processing for HF surface wave radar based on pre-whitened MUSIC［J］．IEEE Journal of Oceanic Engineering，2000，25(4)：458－471．

［4］CAPON J．High resolution frequency wave number spectrum analysis［J］．Proc．IEEE，1969，57：1408 －1418．

［5］SCHMIDT R O．Multiple emitter location and signal parameter estimation［J］．IEEE Trans．on Antennas Propagation，1986，34(3)：276 －280．

［6］ZHANG X F，XU D Z．A novel DOA estimation algorithm based on eigen space［C］．IEEE 2007 International Symposium on Microwave，Antenna，Propagation and EMC Technologies for Wireless Communications．

［7］严颂华，吴世才，吴雄斌．基于神经网络的高频地波雷达目标到达角估计［J］．电子与信息学报，2008，30(2)：339－342．

YAN Song-hua，WU Shi-cai，WU Xiong-bin． DOA estimation based on neural network for HFGWR［J］．Journal of Electronics ＆ Information Technology，2008，30(2)：339－342．

［8］周浩，文必洋，等．基于时频分析的高频雷达目标检测与定向［J］．电子学报，2005，33(12)：2265 －2268．

ZHOU Hao，WEN Bi-yang，et al．Target detection and direction finding with HF radars based on time-frequency analysis［J］．Acta Electronica Sinica，2005，33(12)：2265－2268．

Research on DOA estimation of HFWAR

LU Qing-guang，LIANG Yan-hong，ZHOU Dong-yu
(Institute of Ocean Electromagnetic Environment，Naval University of Engineering，Wuhan 430033，China)

HFSWR has got wide attention and research because of its good performance on BVR detection．As the important part of parameter estimation，how to obtain accurate DOA estimation algorithm is the major work all along．In recent years，as the miniaturization of the array antenna of HFSWR，high resolution algorithm has been studied an applied．In this text，we studied three kind of high resolution algorithm contrastively，based on the features of data of array antenna．It is very significant for project application to provide the choice of algorithm．

HFSWR;DOA;high resolution algorithm

TN911

A

1672－7649(2013)04－0107－04

10.3404/j.issn.1672－7649.2013.04.025

2012－05－03

卢庆广(1989－)，男，硕士研究生，研究方向为信号与信息处理。