视景仿真中运动目标的航迹平滑外推算法

张萍萍，孙永侃，张 莉，林宗祥

(1.海军大连舰艇学院博士队，辽宁大连116018;2.海军大连舰艇学院科研部，辽宁大连116018)

视景仿真中运动目标的航迹平滑外推算法

张萍萍1，孙永侃2，张 莉2，林宗祥1

(1.海军大连舰艇学院博士队，辽宁大连116018;2.海军大连舰艇学院科研部，辽宁大连116018)

为满足视景仿真中运动目标状态的高更新频率的需求，需要对目标进行航迹平滑外推。设计了运动目标的航迹平滑外推算法，建立了目标运动模型和运动目标的航迹平滑外推模型。重点研究了阻塞情况下运动目标的航迹平滑外推的原则和方法。仿真结果及工程应用验证了该算法的有效性。

视景仿真;航迹平滑外推;目标运动模型;跳变;阻塞;阀值

0 引言

水面舰艇作战仿真系统运行过程中，需要对运动目标 (包括舰船、飞行器、导弹等)进行航迹显示，航迹由目标的运动状态信息 (包括位置、航向、航速)来确定。在仿真过程中，目标的运动状态信息一般以秒级的速率发布。如果视景仿真中运动目标的航迹以接收到的信息频率显示，则由于存在跳变现象而无法达到显示要求。因此，需要以1/30 s或更短的时间间隔更新仿真目标的运动状态。为视景仿真的需求，实现视景中目标航迹的平滑无跳变，仿真子系统需要根据接收的目标状态信息和目标当前状态信息对目标未来的运动状态进行推算。本文就视景仿真中的运动目标航迹平滑外推算法进行研究。

1 运动目标航迹平滑外推的基本原则

如图1所示，假设目标状态信息的发送速率为Δt。在视景仿真子系统中，已知t0时刻，目标位置为L0。在t0～t1(ti+1=ti+Δt)时间段内，不发送目标状态信息。为满足仿真需求，视景仿真子系统需要对目标位置进行外推。

图1 目标位置推算原则Fig.1 Reckoning principle of the target position

假设t0时刻开始，目标匀速直线运动，根据t0时刻的位置和航速信息可推算得到t1时刻的目标位置为。则t1时刻，视景仿真子系统中目标位置为。与此同时，视景仿真子系统还不断接收目标状态信息。假设t1时刻，接收到目标位置为L1，则根据目标匀速直线运动的假设，可推算得到t2时刻位置为。

为保证目标的推算航迹与接收到的航迹尽可能一致，应使t2时刻目标的推算位置为。即从t1时刻开始，经过Δt时间，目标应从L'1运动到。根据以上分析，目标的位置推算原则如下：假设目标匀速直线运动，t1时刻目标位于，接收到的目标位置为L1，由目标位置L1推算得到下1个目标位置为，则目标应由位置运动并在t2时刻能够到达位置。

2 运动目标航迹平滑外推的计算模型

如图1所示，已知仿真时刻t0，运动目标的位置 L0(x0，y0，z0)， 速 度 V0(vx0，vy0，vz0)， 航 向 角(目标中心轴线与正北的水平夹角)为φ0，俯仰角(目标中心轴线与水平面的夹角)为θ0，经过Δt时

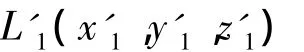
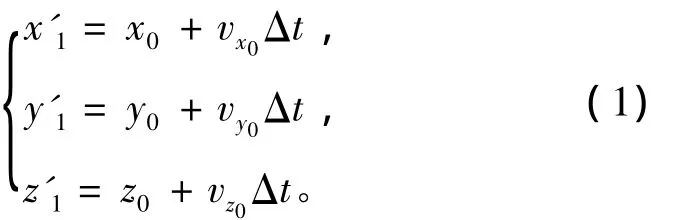
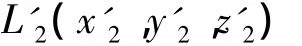
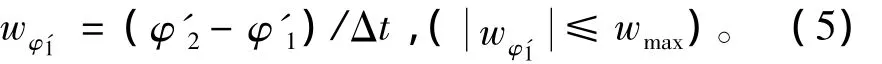
3 阻塞情况下的处理方法

上述运动目标的航迹平滑外推的计算模型适用于目标状态信息能够及时接收到的情况。若仿真系统发生阻塞，可能在一段时间内难以接收到目标信息。此时，视景仿真系统仍需根据以前的目标信息推算位置。当重新接收到目标信息后，目标可能无法从当前位置到达下一个时刻应到达的预定位置。下面对这种情况进行讨论。

3.1 目标可达位置的判断条件

假设t0时刻，目标位置为L0(x0，y0，z0)，速度为V0，航向为 C0，航向角为 φ0，俯仰角为 θ0。由于目标自身性能的限制，在Δt时间内，目标的位置只能在一定的空间范围内变化。假设目标的最大速度为Vmax，最大加速度为amax，最大转向角速度为ωmax。将目标的运动简化为以下3个步骤：①转向到达预定航向;②加速 (或减速)到达预定速度;③匀速运动到预定位置。从t0时刻到t1时刻，目标的速度为V1，航向为C1，则：

设Q为从航向C0到C1的夹角，则

图2 目标以最小速度运动时的可能位置曲面Fig.2 Possible positional surface while the target moves with the minimum velocity

当以最大速度V1=V0+amaxΔt运动时，目标可能的位置为圆锥L0BC，如图3所示。

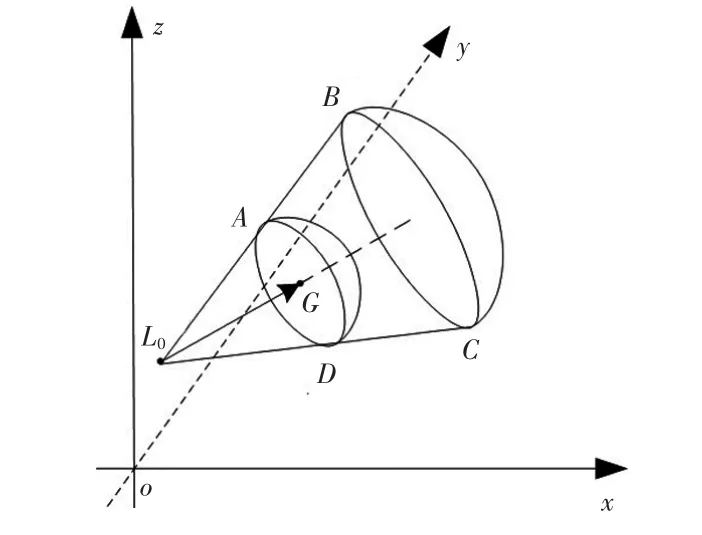
图3 目标以最大速度运动时的可能位置曲面Fig.3 Possible positional surface while the target moves with the maximum velocity

因此，2个曲面之间的空间即为目标可能的位置空间。

设L为下一时刻目标要到达的位置，令V1_min=max{V0－ amaxΔt，0}，V1_max=min{V0+amaxΔt，Vmax}，则L点满足：

且L和L0连线与目标初始航向的夹角∠LL0G满足：

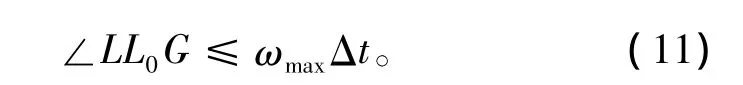
式(10)和式(11)即为目标下一时刻能到达预定位置的判断条件。

3.2 目标预定位置无法达到时的平滑外推模型

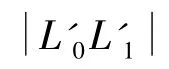
具体求解的数学推导过程如下：

1)若目标在t1时刻在点即使以最大速度也无法到达下一时刻的推算位置点，则令目标以保持航向约束下的最大速度运动到t2时刻，当t2时刻收到新的目标信息后重复上述判断过程。只要判断出目标即使以最大速度也无法到达下一时刻的推算位置，则令目标继续以保持航向约束下的最大速度运动，直到判断出在某一时刻目标以小于或等于最大速度的运动速度能够到达下一时刻的推算位置时，即满足了正常情况的条件，则目标的运动可由正常情况的式(1)～式(3)进行推算。具体数学描述如下：

则推算出目标在L'1点处的运动速度为：

2)同理，若目标在t1时刻在点即使以最小速度运动其位移也超出下一时刻的推算位置运动点，则令目标以最小速度运动到t2时刻，然后在t2时刻重复上述判断过程，只要判断出目标即使以最小速度运动其位移也超出下一时刻的推算位置，则令目标继续以最小速度运动，直到判断出在某一时刻目标以大于或等于最小速度的运动速度能够不超出下一时刻的推算位置时，即满足了正常情况的条件，则目标的运动可由正常情况的式(1)～式(3)进行推算。

3)若目标在t1时刻在点即使以最大转向角速度也无法到达下一时刻的推算航向，则令目标以最大转向角速度运动到t2时刻，然后在t2时刻重复上述判断过程，只要判断出目标即使以最大转向角速度也无法到达下一时刻的推算航向，则令目标继续以最大转向角速度运动，直到判断出在某一时刻目标以小于或等于最大转向角速度运动能够到达下一时刻的推算航向时，则满足了正常情况的条件，目标的转向角速度可由正常情况的式(4)～式(7)进行推算。

3.3 异常情况下的算法处理

由于某些原因，有可能导致阻塞时间较长，有可能持续几秒都收不到目标的状态信息。此时，为保证仿真系统的平稳运行，仿真子系统应根据仿真时间的推进对目标状态进行合理外推。

在这种情况下，目标将以阻塞前最后一次收到的状态信息进行推算，推算方法采用本文前面所述的方法。当阻塞结束，仿真子系统收到导演部发布的位置和状态信息时，由于阻塞时间间隔长，目标当前的推算位置和状态可能与当前收到的位置和状态信息产生较大偏差，当偏差超出允许的精度时，可以考虑使目标跳变到所收到的实际位置，此时可以根据仿真精度的需求设置阀值，作为跳变的判断条件。

4 仿真结果与分析

为验证该算法的有效性，对收到的原始目标运动数据进行平滑处理，为检验各种复杂运动状态下的预测效果，选用一组包含多种运动状态的数据进行预测。这组数据可理解为运动目标从0 s开始以初速度为0 m/s，加速度为2 m/s2运动5 s，然后俯仰角从0°以角速度为1°/s抬高至5°，再保持姿态运动3 s，随后俯仰角从5°以角速度－1°/s降为0°，横滚角从0°以角速度5°/s左倾为－10°，并左转弯30°后调平其姿态，然以1 m/s2的加速度运动。

仿真结果表明，平滑处理前的运动轨迹 (见图4)是由时间间隔为1 s的点组成的，这将导致视景显示中运动目标的轨迹显示为断续的跳变点迹，这样的显示效果无法达到视景仿真的精度需求。

运用本文提出的算法进行平滑处理后的运动轨迹如图5所示。由图可见，平滑后的运动轨迹与原始位置数据吻合精准，且实现了轨迹的平滑。由图6～图8可见，平滑后的轨迹在东向、北向和高度3个方向上均实现了与原始数据的精准拟合。可见，该算法对运动目标航迹的推算精度较高，同时实现了轨迹的平滑。

图4 平滑前的航迹图Fig.4 Unsmoothed trajectory graph

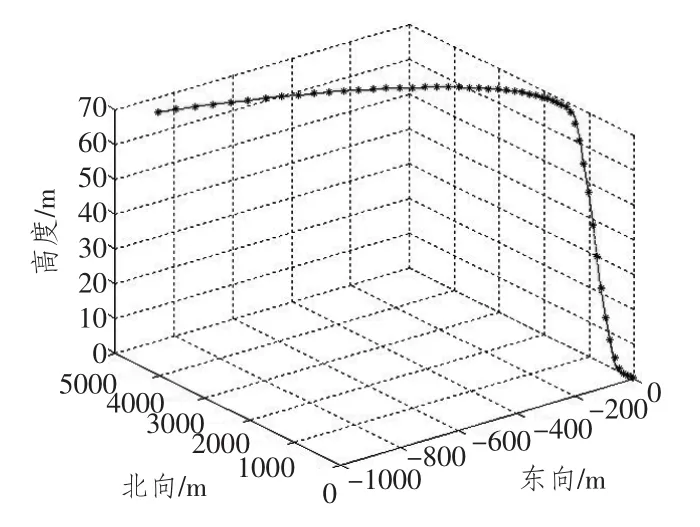
图5 平滑后的航迹图Fig.5 Smooth trajectory graph

图6 航迹东向平滑图Fig.6 Eastward smooth trajectory graph

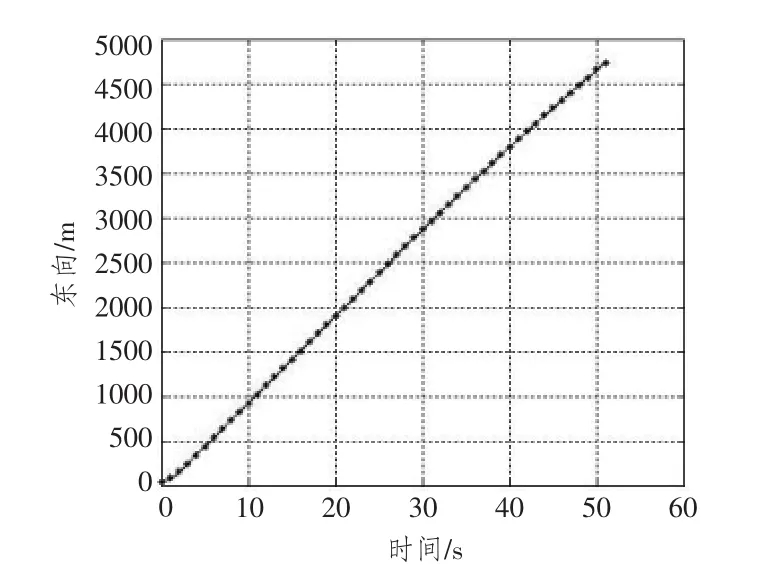
图7 航迹北向平滑图Fig.7 Northward smooth trajectory graph

图8 航迹高度平滑图Fig.8 Height smooth trajectory graph

5 结语

本文提出的视景仿真中运动目标的航迹平滑外推算法解决了仿真目标运动航迹的跳变问题，考虑了目标状态信息阻塞情况下的处理，使仿真目标的运动航迹显示达到了仿真要求。上述算法在实现仿真运动目标航迹平滑的同时，以牺牲一定的精度为代价，使目标的运动状态与实际产生一定误差。后续工作应使算法在实现航迹平滑外推的同时尽量提高推算精度。

［1］王艳.船舶航迹保持算法的研究与实现［D］.哈尔滨：哈尔滨工程大学，2008.

WANG Yan.Research and realization of the alporithm onthe ship track keeping［D］.Harbin：Harbin Engineering University，2008.

［2］鞠世琼.船舶航迹舵控制技术研究与设计［D］.哈尔滨：哈尔滨工程大学，2007.

JU Shi－qiong.The research and design ofthe ship coursecontrolautopilot［D］.Harbin：Harbin Engineering University，2007.

［3］王继森.船舶航迹智能控制系统研究［D］.哈尔滨：哈尔滨工程大学，2008.

WANG Ji－sen.Study ofintelligentcontrolsystem of shiptrack［D］.Harbin：Harbin Engineering University，2008.

［4］朱志宇.基于UKF的闪烁噪声机动目标跟踪［J］.计算机仿真，2007，24(11)：120 －123.

ZHU Zhi－yu.Unscented Kalman filterformaneuver targettracking under glint noise［J］.Computer Simulation，2007，24(11)：120 －123.

［5］吕泽均，肖先赐.基于时延分数阶相关函数时空处理的子空间测向算法［J］.信号处理，2003(1)：51－54.

LV Ze－jun，XIAO Xian－ci.A subspace－based directionfinding algorithm using temporal and spatial processing oftime lag fractonal order correlation function［J］.Signal Processing，2003(1)：52－54.

［6］HAOM S，et al.Signal processing with fractional lowerorder moments：stable processes and their applications［J］.Proceedings of the IEEE，1993，87(1)：986 －1010.

［7］CHAMBERS J A，TANRIKULU O，CONSTANTINIDES AG.Least mean mixed － norm adaptive filtering［J］.Electronics Letters，1994，30(19)：1574 －1575.

［8］BODENSCHATZ J S，NIKAS C L.Symmetric alpha－stablefilter theory［J］.IEEE Transactions on Signal Processing.1997，45(9)：2301－2306.

［9］MA X Y.Robust signal processing in impulsive noise withstable distributions：estimation，identification andequalization［D］.USA：A BELL＆Howell Information Company，University of Southern California，1996.

［10］DAEIPOUR E，BAR－SHALOM Y.An interacting multiplemodel approach for target tracking with glint noise［C］.Record of the IEEE National，Radar Conference，1994.

［11］GEORGIOU P G.Alpha－stable modeling of noise and robusttimedelay estimation in the presence of implusive noise［J］.IEEE Transactions on Multimedia，1999，1(3)：291 －301.

Algorithm research on smooth track extrapolation of moving target in scene simulation

ZHANG Ping－ping1，SUN Yong－kan2，ZHANG Li2，LIN Zong－xiang1
(1.PHD Team，Dalian Naval Academy，Dalian 116018，China;2.Department of Scientific Research，Dalian Naval Academy，Dalian 116018，China)

In order to meet the requirements of highly update frequency of moving target's state in scene simulation system，smooth track extrapolation of moving target is needed.A smooth track extrapolation algorithm is proposed，the kinematic model and smooth track extrapolation model of moving target are established.Principle and method of smooth track extrapolation in conditions of congestion is mainly researched.The simulation result and engineering application show the effectiveness of the method.

scene simulation;smooth track extrapolation;jump;congestion;threshold value

TP391.9

A

1672－7649(2013)04－0049－05

10.3404/j.issn.1672－7649.2013.04.011

2012－08－06;

2012－08－23

张萍萍(1975－)，女，博士研究生，研究方向为舰艇作战仿真。