流体系统网络变流阻系数解算方法

廖金军，邹学新，李宝仁

(1．华中科技大学机械科学与工程学院，湖北武汉430074;2．中国铁建重工集团有限公司，湖南长沙410100;3．第二炮兵工程大学士官学院教研部，山东青州262500)

流体系统网络变流阻系数解算方法

廖金军1，2，邹学新3，李宝仁1

(1．华中科技大学机械科学与工程学院，湖北武汉430074;2．中国铁建重工集团有限公司，湖南长沙410100;3．第二炮兵工程大学士官学院教研部，山东青州262500)

现代计算方法和手段的进步，使得基于图论的流体网络解算方法研究不断深入。针对流体网络图论解算算法，分解了拟牛顿法的解算过程，并结合实际流体网络，首次提出了流体系统网络变流阻系数的解算方法，分析了采用管路恒流阻系数和变流阻系数的拟牛顿法在实际流体网络解算中的差异。计算结果表明：采用变流阻系数的拟牛顿法能够提高当流量初始化值与迭代收敛值相差较大时流体系统网络解算的精度，变流阻系数解算法为提高大型、复杂流体系统网络解算精度提供了一种有效的方法。

流体系统网络;图论;拟牛顿法;变流阻系数

0 引言

随着计算机技术的发展，网络图论在流体系统网络中的应用已日益广泛［1］。网络图论又称网络拓扑理论，它是通过网络拓扑关系，并通过分析网络各元素的空间和特性参数等，实现对网络特性的多方位分析和衡量［2］。将流体系统网络中的管段抽象成一条分支，分支与分支通过节点相连，将流体系统管网图转化成为图论意义上网络图，而且对于一般的流体网络中，各管道中流体流动具有方向性，如果定义网络图中分支的方向为其内部流体流动的方向，则此时网络图就是有向网络图［3］。网络图论方法作为网络分析的主要手段和工具，在流体系统网络水力特性分析中，结合矩阵计算技术，既能充分发挥图论理论的优势，使系统建模和仿真计算过程快捷、准确，同时扩展和丰富了流体系统分析的内容和手段［4］。

现有基于图论建模和分析的流体系统网络解算算法，通常以采用恒流阻系数的拟牛顿法或者哈代－克罗斯迭代算法为主，以上算法中忽略了流体系统网络流量迭代中修正流量对解算结果的影响［5］，在管路雷诺数变化较大的流体系统网络中，管路流阻系数将发生明显的变化，其对系统网络解算的影响不容忽视，特别是对于流体流态对系统分析结果影响较大的流体网络。因此，基于以上分析，采用变流阻系数的迭代算法，在计算中实时更新任意迭代时步的流阻系数，以提高系统网络解算的精度。

1 流体网络解算原理

1.1 网络节点流量守恒

从流体网络节点流量守恒定律可知，流体系统网络图G=(V，E)，具有网络节点数m=|V|，网络分支数n=|E|，系统网络可以列出m个节点流量守恒方程，且m个节点流量守恒方程可表示为［6］

式中：B=(bij)m×n为系统网络G的关联矩阵;Q=(q1，q2，q3，…，qn)为网络分支流量矩阵，其元素排列次序与系统网络关联矩阵一致;QT为Q的转置矩阵。

1.2 系统回路能量守恒

按照系统网络回路矩阵C=(cij)l×m的分支顺序排列，回路能量守恒方程可用回路阻力矩阵H=(h1，h2，h3，…，hn)和回路附加阻力矩阵 H'=(h'1，h'2，h'3，…，h'n)表示为

式(2)也可改写为

式中：HT和H'T分别为H和H'的转置矩阵;l为回路总数。

1.3 系统回路阻力平衡

流体系统网络运行时，流体流动在管网中的压降 (习惯上也称阻力，能量损失、压力损失等)由达西公式得：

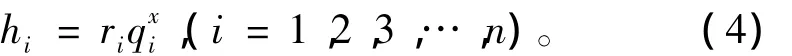
式中：hi为各网络分支ei∈C上的阻力压降;ri为对应分支上的阻力值;qi为对应分支上的流量值;x为对应分支上的流态因子。流态因子取决于流体在对应分支中的流动状态，当流动状态为层流时，x取1;当流动状态为紊流时，x取2;过渡状态流时，x在1～2之间取值。

由于管路雷诺数对流阻系数影响较大，直接影响着系统网络分支流阻值的计算。因此，从提高系统网络解算精度出发，提出采用变阻力系数迭代法，在计算过程中动态更新系统网络各分支管路中雷诺数的计算。

根据图论理论，系统网络图G的基本关联矩阵Bk和基本回路矩阵Ck的秩分别为rank(Bk)=m－1和rank(Ck)=n－m+1;根据流量守恒方程，如果定义系统流体网络各分支流量为未知数，则通过系统网络图基本关联矩阵可以构造出m－1个线性无关的n元一次方程组。同理，根据能量守恒方程，确定系统网络各分支流阻值后，利用系统网络图基本回路矩阵可以构造出n－m+1个线性无关的n元二次非线性方程组，于是联立流量守恒和能量守恒方程可得到(m－1)+(n－m+1)=n个n元线性无关的方程组：式中：bij和cij分别为流体系统网络图G的基本关联矩阵Bk和基本回路矩阵Ck的元素;qj为系统网络分支流量;fi为回路阻力平衡方程。f(ri，qj，Re)为回路各分支动态阻力矩阵，其是根据系统网络管路的流态而得的分段函数

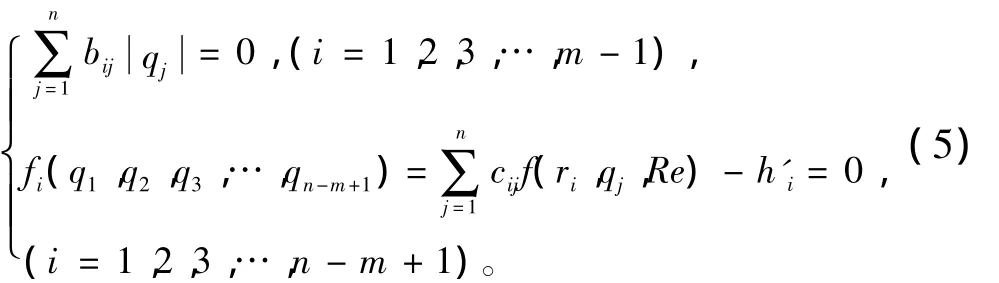
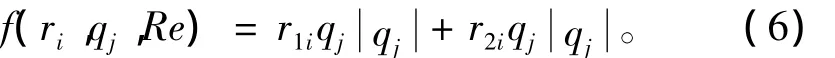
式中：r1i为流体系统网络支路管路附件、弯头、变径管和多通接头时的阻力系数矩阵元素;r2i为流体系统网络支路管段阻力系数矩阵元素。

流体流经管路附件、变径管、弯头和多通接头的阻力系数统一迭算为

式中：hak和qak分别为系统网络第i支路上第k个阀门工作时，对应的压降和流量;ξb为弯头局部阻力系数;ξd为渐扩管局部阻力系数;ξt为渐缩管局部阻力系数;ξse为突扩管局部阻力系数;ξsc为突缩管局部阻力系数;ξc为多通接头局部阻力系数。

将流体流经系统网络支路直管的沿程阻力系数跌算为r2i，其表达式为

式中：li为第i支路中直管段的长度;di为第i支路管道通径;Si为第i支路管道截面积。

2 流体网络分析迭代步骤

1)回路能量守恒方程Taylor展开

按照系统网络节点流量守恒定律，初始化系统网络各分支流量，其矩阵表达式为

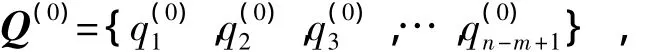
将系统网络回路能量守恒方程组进行Taylor展开，能量守恒方程 fi(q1，q2，q3，…，qn－m+1)在第 k 次展开 (k=1，2，3，…)的表达式为

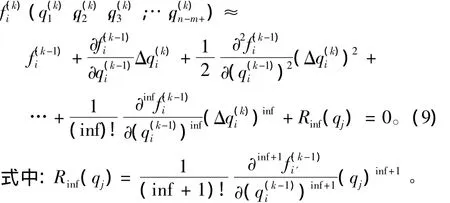
式(9)可用矩阵形式表示为：

2)修正余支流量矩阵

根据式(11)得余支流量修正矩阵ΔQ(k)L为则余支流量修正为

3)修正树枝流量矩阵

根据图论理论中基本关联矩阵和基本回路矩阵之间的转换关系，树枝流量修正矩阵Q(k)T可表示为

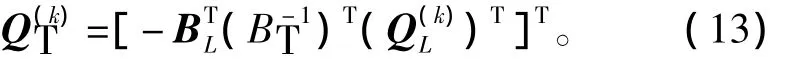
4)迭代误差判别

由于在式(9)中忽略了第k次迭代前的函数初始二阶导数矩阵，因此存在舍入误差。为保证系统网络解算的计算精度，采用第k次迭代后余支流量修正矩阵和第k次迭代后回路阻力函数矩阵的行和范数作为迭代误差的判别条件：

5)更新网络流阻系数矩阵

经过迭代后，系统网络余支和树枝流量矩阵往往不能立即收敛，需要在修正流量矩阵的基础上进行迭代。同时，由于经过修正的流量，其值发生改变，这将直接引起该时步流阻系数矩阵的变化，采用恒流阻系数法迭代，忽略其影响。因此，为了提高系统网络解算精度，将该时步流阻系数矩阵进行迭代更新，以体现流量修正对其流阻系数的影响，流阻系数在k+1步迭代时的更新值为

3 计算实例

流体系统的工作原理和系统流阻系数分别如图1和表1所示。按照给定参数，根据上述流体系统网络解算原理和变流阻迭代算法，完成对流体系统网络解算。

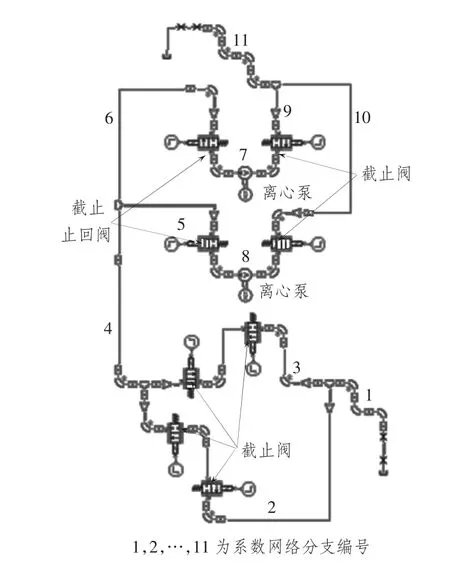
图1 流体系统工作原理Fig.1 The principle of system work

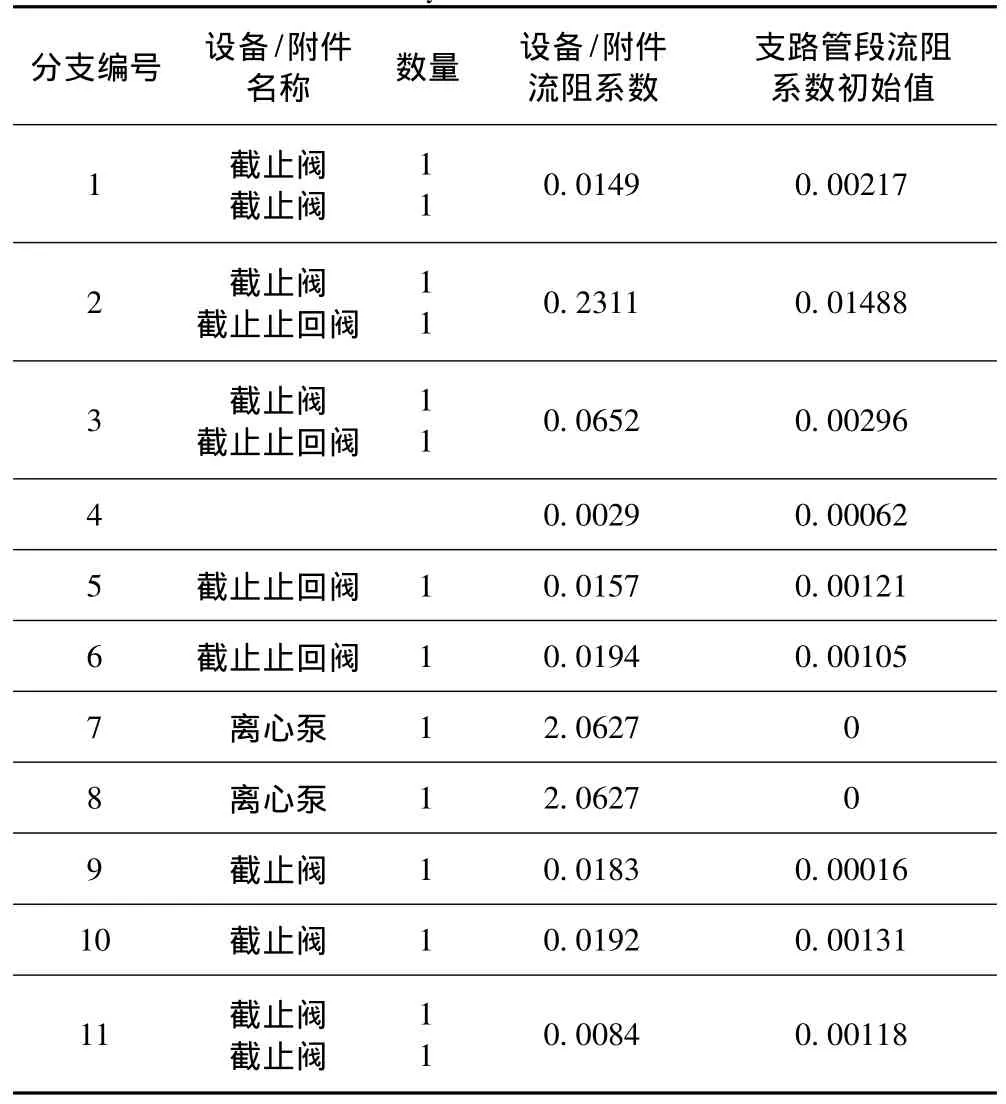
表1 系统流阻系数表Tab.1 System flow resistance

4 结果对比

恒流阻迭代法以支路管段流阻系数初始值进行迭代，解算过程中流阻系数不发生变化，而变流阻迭代法通过支路管段流阻系数初始值进行初始迭代，在下一时步将管路流阻系数根据系统流量修正值进行更新计算，得到新的管路流阻系数并进行迭代。以下对系统分别采用恒流阻和变流阻迭代方法进行网络解算，其计算结果如图2～图5所示。

采用恒流阻和变流阻系数迭代法解算，得到支路7离心泵流量分别为33.51 t/h和33.52 t/h(如图2所示)，二者相差0.01 t/h。

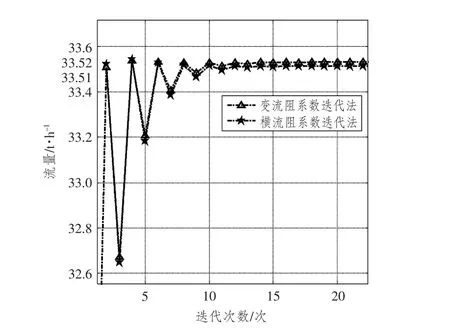
图2 支路7离心泵流量解算Fig.2 The flow calculation of centrifugal pump in branch 7

采用恒流阻和变流阻系数迭代法解算，得到支路8离心泵流量分别为31.43 t/h和31.45 t/h(如图3所示)，二者相差0.02 t/h。

图3 支路8离心泵流量解算Fig.3 The flow calculation of centrifugal pump in branch 8

采用恒流阻和变流阻系数迭代法解算，得到支路2流量分别为22.6 t/h和22.54 t/h(如图4所示)，二者相差0.06 t/h。

图4 支路2流量解算Fig.4 Flow calculation in branch 2

采用恒流阻和变流阻系数迭代法解算，得到支路3流量分别为42.34 t/h和42.43 t/h(如图5所示)，二者相差0.09 t/h。

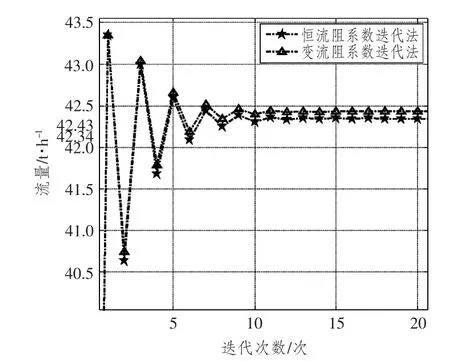
图5 支路3流量解算Fig.5 Flow calculation in branch 3

从以上数据分析可以看出，系统流量修正对系统网络流量解算结果有影响，而且由于流量修正矩阵的非一致性，因系统流量修正引起的系统网络解算结果的变化由系统阻力矩阵决定。

5 结语

通过对系统网络流量解算算法和迭代过程的分析，提出了变流阻系数的迭代算法，针对实际流体网络系统，分别采用恒流阻系数和变流阻系数迭代方法进行系统网络流量求解，从解算结果对比分析中可以发现，原有采用恒流阻系数的网络流量迭代算法，存在忽略系统流量初始化对系统解算结果的影响，而系统固有阻力特性矩阵将决定其对系统解算结果的影响程度。

因此，为进一步提高流体系统网络流量的解算精度，变流阻系数迭代算法将是有效的保证。

［1］卢开澄，卢华明．图论及其应用［M］．北京：清华大学出版社，2005．

［2］张立勇．供热管网的流体网络分析及水力平衡研究［D］．天津：天津大学，2003．

［3］KESAVAN H K，CHANDRASHEKAR M．Graph-theoretic models for pipe network analysis［J］．Journal of The Hydraulics Division，ASCE，1972(10)：55 －61．

［4］FIGUEIREDO R，LIU Ben-yuan，GUO Yang．On the effieieney of fluid simulation of networks［J］．Computer Networks，2006，50(12)：1974 －1994．

［5］KOROLEVA O I，KLSTIE M．Averaging analysis of periodically foreed fluid networks［J］．Automatiea，2005，41(l)：129－135．

［6］刘剑，贾进章，郑丹．流体网络理论［M］．北京：煤炭工业出版社，2002．

［7］李聪江，郑书兵，张志峰．矿井通风计算机模拟系统的应用［J］．煤矿开采，2006，51(3)：45－52．

［8］陈彬．舵机电液伺服调节器耦合振动特性及其控制研究［D］．武汉：华中科技大学，2007．40 －42．

Study on variable flow resistance method for analysis on fluid system network

LIAO Jin-jun1，2，ZOU Xue-xin3，LI Bao-ren1
(1．School of Mechanical Science and Engineering，Huazhong University of Science and Technology，Wuhan 430074，China;2．China Railway Construction Heavy Industry Co．Ltd．，Changsha 410100，China;3．Officer College of The Second Artillery Engineering University，Qingzhou 262500，China)

With the development of modern calculation means，the research of fluid network numerical method based on graph-theory becoming more deep．In connection with the numerical method analyzing fluid network based on graph-theory，the process of quasi-Newton method is decomposed，then，integrating with a practical fluid system，the difference between the method of constant resistance and variable resistance used to compute the system is analyzed，and the calculation results shows that using the variable resistance method can prove the precision of calculation，when the system initial flow and the iterative convergence value is large different．The variable resistance method can also be used for a large and complex fluid system．

fluid system network;graph-theory;quasi-Newton method;variable flow resistance method

TH38;TK79

A

1672－7649(2013)04－0040－05

10.3404/j.issn.1672－7649.2013.04.009

2011－05－20;

2013－03－01

廖金军(1982－)，男，博士，工程师，研究方向为流体传动与控制，电液比例、伺服控制和流体系统网络特性等。