水下爆炸作用下固支平板动态响应分析

吴国民，周心桃，李 俊

(中国舰船研究设计中心，湖北武汉430064)

水下爆炸作用下固支平板动态响应分析

吴国民，周心桃，李 俊

(中国舰船研究设计中心，湖北武汉430064)

基于MSC．Dytran软件，对固支平板在水下非接触爆炸作用下的动态响应试验工况进行建模仿真分析，其计算结果与试验结果吻合较好。得到的平板在不同大小的水下爆炸冲击波载荷作用下的失效模式也与试验相一致，由此说明利用有限元软件MSC．Dytran模拟仿真水下爆炸作用下的结构动态响应过程的可行性，为工程应用提供了借鉴和参考。

水下爆炸;固支平板;动态响应;MSC．Dytran

0 引言

舰船在作战使用过程中可能遭到来自鱼雷、水雷等武器的水下爆炸冲击，而舰船的外板板格作为承受水下爆炸冲击的直接作用对象，其动态响应特性是舰船设计关注的重要方面，因此，国内外学者对平板在水下爆炸冲击波作用下的动态响应进行了大量的研究。K.Ramajeyathilagam进行了一系列水下爆炸作用下的固支平板动态响应试验，研究固支平板在不同冲击因子作用下的失效模式［1－2］;朱锡等针对固支方板在爆炸载荷作用下的应变场和破裂形式进行了试验和理论分析，并给出破裂临界压力值［3］;相对于成本较高的水下爆炸试验而言，更多学者选择利用数值仿真分析方法对该问题进行研究，如金乾坤、谭海涛等分别利用有限元软件 LSDYNA、ABAQUS对平板在水下爆炸冲击波作用下的塑性动力响应进行了数值仿真分析，其计算精度也得到了一定的验证［4－6］。而本文则主要利用有限元软件MSC.Dytran对水下爆炸作用下固支平板的动态响应特性进行计算模拟分析。为便于验证数值仿真计算方法，选取文献 ［2］中的试验工况进行数值仿真建模，然后将数值仿真结果与试验结果进行对比，以验证数值仿真计算方法的准确性。

1 水下爆炸作用下固支平板动态响应仿真

1.1 有限元建模

文献 ［2］中将尺寸为0.55m×0.45m×0.002m的钢制平板四周用螺栓紧固在箱体强力框架上，然后置于水中进行不同药量的水下爆炸试验，平板的背爆面由箱体形成空腔，平板的试验目标区域即迎爆面区域大小为0.30m×0.25m，药包位于平板中心法向0.15 m处，药包药量分别为10g，20g，30g，40g，50g，60g，70g和80g，分别对应工况1～工况8。针对上述试验模型在MSC.Dytran软件中建立有限元模型如图1所示，平板四周采用固支边界条件，水域大小为0.30m×0.25m×0.35m，平板与水域之间采用ALE耦合方式。试验在15m×12m×10m的爆炸水池中进行，药包置于水池中心水深2 m处，因此，除耦合面外水域的其余5个面用FLOWDEF卡片定义为无反射流出边界。平板被划分为3 000个4节点shell单元，整个水域划分为270 000个8节点六面体欧拉单元。

图1 有限元模型Fig.1 The finite-element model

1.2 材料模型

上述有限元模型中共有炸药、水和钢板3种材料，对于欧拉网格中的炸药和水分别利用状态方程来定义其压力与密度及比内能之间的函数关系，对于钢板采用考虑应变率效应的Cowper-Symonds本构模型，具体如下：

1)炸药的状态方程

炸药爆炸过程用下列JWL状态方程 (EOSJWL)来模拟：

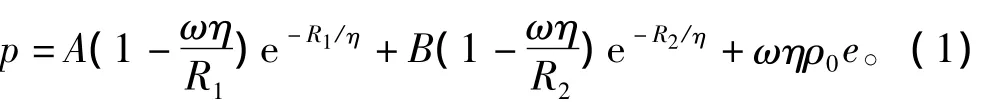
式中：η=ρ/ρ0，ρ0为炸药的初始密度，ρ为材料整体密度;e为单位质量比内能;A，B，ω，R1及R2为常数。

文献 ［2］中使用的是PEK-1型塑胶炸药，将其转化为1.17倍的TNT炸药当量进行数值仿真计算。对于TNT炸药，密度为1 580 kg/m3，比内能为4.19 MJ/kg，初始爆轰波速度为6 930 m/s，A=371.2 GPa，B=3.231 GPa，ω =0.3，R1=4.15，R2=0.95。

2)水的状态方程

在绝热的条件下，水的状态方程可用下式表示［7］：

其中：p为压力;ρ0为水在常温状态下的密度;ρ为整体密度;B和n为常数，B=3 045 kg/cm2，n=7.15。在MSC.Dytran中，水的状态方程用多项式状态方程 (EOSPOL)来模拟，其中压力是相对体积及比内能的多项式函数［8］：

p=a1μ +a2μ2+a3μ3+(b0+b1μ +b2μ2+b3μ3)ρ0e。 (3)式中：e为单位质量比内能;μ=(ρ/ρ0) －1。计算中，取p=a1μ，体积模量a1=2.2 GPa，取ρ0=1 000 kg/m3，e=83.950 kJ/kg。

3)钢板的本构模型

该钢板密度为7 860 kg/m3，弹性模量为210 GPa，剪切模量为250 MPa，泊松比为0.3，静态屈服应力为300 MPa，极限拉伸应力为380 MPa，失效应变为0.36。由于该低碳钢板属于应变率敏感材料，在水下爆炸作用下有应变率强化效应，因此钢板在数值仿真中采用如下的Cowper-Symonds模型：

其中：σd为动态屈服应力;σs为静态屈服应力;ε·为等效应变率;D和q为应变率强化效应的参数，一般取D=40/s，q=5。

1.3 计算结果分析

1)水下爆炸冲击波压力计算结果

在平板中心法线方向，选择离药包中心0.15 m处31531号单元作为考核点，考核该处的冲击波压力峰值及随时间的变化规律。根据前述试验条件，该考核点初期的水下爆炸冲击波传递边界条件近似于自由场，对于自由场中水下爆炸冲击波的传递，库尔在早期提出了如下的冲击波压力峰值及时历变化计算经验公式［9］，并得到了广泛认可，可用作仿真计算结果校核：

式中：Pm为冲击波压力峰值，Pa;W为TNT球状药包质量，kg;R为爆心到测点的距离，m;R0为药包的初始半径，m;θ为冲击波时间衰减常数，s;为 R/R。

工况1中31531号单元的冲击波压力时历曲线如图2所示，其中数值仿真计算的冲击波压力峰值为79.5 MPa，而利用上述经验公式计算得出的冲击波压力峰值为83.7 MPa，数值仿真的计算结果误差约为5%，而数值仿真得到的冲击波衰减规律也与经验公式中的指数衰减规律较吻合。各个工况对应的考核点31531号单元的峰值压力仿真计算结果与经验公式计算结果对比见图3。从图中可知，各工况的数值仿真结果均与经验公式计算结果相差不大，之所以药量小的工况数值仿真结果偏小，而药量大的工况数值仿真结果偏大，这是因为在水下爆炸数值仿真中，冲击波压力计算值与水域欧拉单元的网格密度有较大关系，单元网格尺寸与药包半径满足一定的比例关系时，仿真结果才能达到较好的精度［10］。本文计算中，各工况的网格尺寸不变，变化的是药包质量即半径，因此，数值仿真结果出现前面偏小后面偏大的情况。经过大量的计算表明，针对不同的药包半径调整响应的网格密度，各个工况考核点处的压力值都可以得到更高精度的仿真结果。

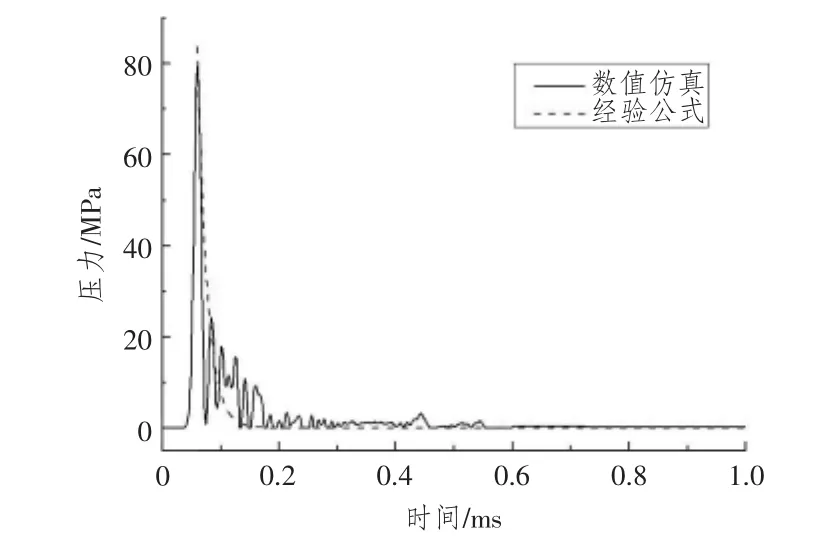
图2 31531号单元 (离爆心0.15 m处)冲击波压力时历曲线数值仿真与经验公式的对比Fig.2 The comparison of shock wave pressure-time between simulation and experimental formulations(element 31531，0.15 m from the center of the charge)

图3 各工况31531号单元冲击波压力峰值计算值与经验公式的对比Fig.2 The comparison of peak pressure between simulation and experimental formulations with 8 cases(element 31531，0.15 m from the center of the charge)

2)平板中心位移计算结果

由上述有限元模型计算得到的前5个工况下的平板中心位移结果与试验结果对比如表1所示。

表1 平板中心位移计算结果与试验结果对比Tab.1 The comparison of the flat plate's central displacement between simulation and experiment

从表1中的数据可以看出，除工况5误差较大外，其他工况的平板中心位移计算结果均与试验结果较吻合。大部分的计算结果与试验结果相比均有所偏小，这是由于计算中选用的是平板固支边界条件，而试验中平板是用螺栓紧固，平板在爆炸冲击瞬态作用下其边界处产生较大的滑移变形。从试验照片来看，药量越大的工况，此滑移变形效应越突出，平板上的部分螺栓孔孔径在上述拉伸变形作用下明显增大，在未测得平板中心最终位移的工况7和工况8中，平板四周甚至有一边沿着螺栓孔被完全撕毁断裂。

对于工况6，试验测得平板中心点最终位移为0.125 m，并且在平板的边界处和板中心附近出现破裂，数值仿真结果显示，平板在板的边界处和板中心附近等效塑性应变均超过失效应变值0.36，出现了与试验结果类似的破坏模式，但板中心位移已经不是变形位移，无法与试验结果进行比对。

3)平板3种失效模式分析

固支平板在空中爆炸冲击波作用下有3种失效模式，即模式Ⅰ：塑性大变形;模式Ⅱ：边界处拉伸断裂失效;模式Ⅲ：边界处剪切断裂失效［11］。而固支平板在不同大小的水下爆炸冲击波作用下同样呈现出上述3种失效模式［2］。

选取典型的工况1、工况6和工况8的计算结果进行分析。由于计算模型定义的是最大塑性应变为0.36的材料失效判据，因此，对比分析上述3个工况同一时刻的塑性应变分布规律。工况1、工况6和工况8中平板在t=0.000 8 s时的等效塑性应变分布规律如图4所示。从图中可看出，对于工况1，该时刻平板中间部位产生较大的塑性变形，其次是边界部位，而中间部位的等效塑性应变比边界部位大一个量级;对于工况6，同样是平板中间部位和边界部位产生很大的塑性变形，但二者等效塑性应变的量级相当，并且在平板的长边边界处等效塑性应变已经超过定义的失效塑性应变值而发生破裂;而在工况8，边界部位的等效塑性应变值要比中间部位大很多，并且平板的4个边界处的等效塑性应变均超过了失效塑性应变值，4个边界均产生了破裂。

图4 t=0.000 8 s时等效塑性应变分布云图Fig.4 The effective plastic strain's contour at t=0.000 8 s

进一步提取平板x方向 (即长边方向)中心线处在t=0.000 2 s，t=0.000 5 s和t=0.000 8 s三个时刻的等效塑性应变数据，分析其动态响应变化规律如图5所示。从图中可以看出，平板的动态响应初始阶段，均是边界处先产生相对较大的塑性变形。随着冲击波的进一步作用，工况1中平板中间部位的塑性变形迅速增加，而边界处的塑性变形变化不大;工况2中则是平板中间部位和边界部位的塑性变形同步增加，产生较强的面内拉伸作用;工况3与工况1相反，平板边界处的塑性变形迅速增加，而中间部位的塑性变形变化相对较小，且比较均匀，这是因为边界处由于剪切作用，很快发生了剪切断裂，整块板形成了一种冲塞式的剪切破坏。

上述3个工况数值仿真得出的平板失效模式与试验结果完全一致，即，工况1属于塑性大变形的失效模式Ⅰ，工况6属于边界处拉伸断裂的失效模式Ⅱ，工况8属于边界处剪切断裂的失效模式Ⅲ。

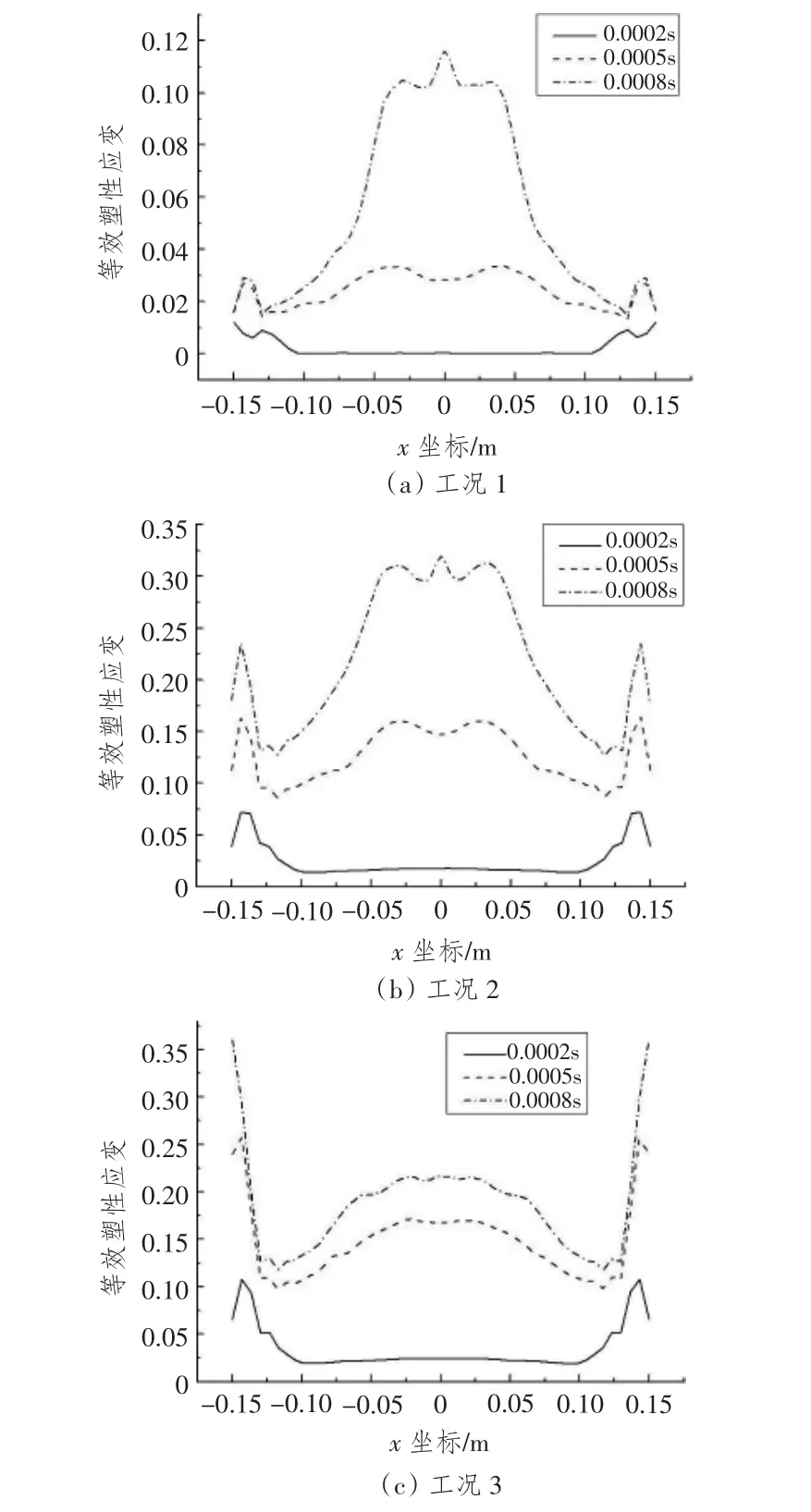
图5 平板x方向中心线处不同时刻的等效塑性应变Fig.5 The effective plastic strain on the plate's central line in x direction

2 结语

本文利用大型通用有限元软件MSC.Dytran对固支平板在水下非接触爆炸作用下的试验工况进行了建模仿真分析，模拟得到的水下爆炸冲击波压力和平板中心位移分别与理论值和试验结果吻合较好，分析得到的平板在不同大小的水下爆炸冲击波载荷作用下的失效模式也与试验结果相一致，说明通过选择合适的材料方程、边界条件以及网格划分等，可利用有限元软件MSC.Dytran较好地模拟仿真水下爆炸作用下的结构动态响应过程，为实际工程应用提供了借鉴和参考。

［1］RAMAJEYATHILAGAM K，VENDHAN C P，BHUJANGA V R．Non-linear transient dynamic response of rectangular plates under shock loading［J］．International Journal of Impact Engineering，2000(24)：999 －1015．

［2］RAMAJEYATHILAGAM K，VENDHANB C P．Deformation and rupture ofthin rectangularplates subjected to underwater shock［J］．International Journal of Impact Engineering，2004(30)：699 －719．

［3］朱锡，冯刚，张振华．爆炸载荷作用下固支方板的应变场及破坏分析［J］．船舶力学，2005(2)：83－89．

ZHU Xi，FENG Gang，ZHANG Zhen-hua．Strain field and damage analysis of clamped square plates subjected to explosive loading［J］．Journal of Ship Mechanics，2005(2)：83 －89．

［4］金乾坤，丁刚毅．水下爆炸对船板冲击作用仿真［J］．计算机仿真，2005(6)：28－31．

JIN Qian-kun，DING Gang-yi．Computer simulation of response of ship hull to underwater shock［J］．Computer Simulation，2005(6)：28 －31．

［5］谭海涛，王善．水下爆炸载荷作用下空背板动态响应研究［J］．船海工程，2009(5)：50－53．

TAN Hai-tao，WANG Shan．Dynamic response of air-backed plate under underwater explosion［J］．Ship ＆ Ocean Engineering，2009(5)：50 －53．

［6］贾宪振，胡毅亭，董明荣，等．水下爆炸冲击波作用下平板塑性动力响应的数值模拟［J］．舰船科学技术，2007，29(6)：41－44．

JIA Xian-zhen，HU Yi-ting，DONG Ming-rong，et al．Numerical simulation of dynamic plastic response of flat plates subjected to underwater explosion shock waves［J］．Ship Science and Technology，2007，29(6)：41 －44．

［7］J．亨利奇．爆炸动力学及其应用［M］．熊建国，等译．北京：科学出版社，1987．

［8］MSC．Dytran User's Manual．MSC Corporation，2008．

［9］库尔．水下爆炸［M］．罗耀杰，等译．北京：国防工业出版社，1960．

［10］张振华，朱锡，白雪飞．水下爆炸冲击波的数值模拟研究［J］．爆炸与冲击，2004(2)：182 －188．

ZHANG Zhen-hua，ZHU Xi，BAI Xue-fei．The study on numerical simulation ofunderwaterblastwave［J］．Explosion and Shock Waves，2004(2)：182 － 188．

［11］OLSON M D，NURICK G N，FAGNAN J R．Deformation and rupture of blast loaded square plates－predictions and experiments［J］．International Journal of Impact Engineering，1993(23)：279－291．

Dynamical response of flat plates subjected to underwater explosion

WU Guo-min，ZHOU Xin-tao，LI Jun
(China Ship Development and Design Center，Wuhan 430064，China)

Using the software MSC．Dytran，the experiments about dynamical response of flat plates subjected to underwater explosion were simulated by numerical model．The results of numerical simulation were agreeable with the ones of the experiments．The failure modes of the plats subjected to different underwater explosions in simulation were also consistent with the results of the experiments．So it is feasible to simulate dynamical response of structures subjected to underwater explosion by MSC．Dytran，and it can be used for reference to the actual engineering problems．

underwater explosion;flat plate;fynamical response;MSC．Dytran

O383+．1;TP391．9

A

1672－7649(2013)04－0025－04

10.3404/j.issn.1672－7649.2013.04.006

2012－10－19;

2012－11－26

吴国民(1980－)，男，博士研究生，工程师，研究方向为水面舰船结构抗爆抗冲击设计。