超声作用下水中微气泡的运动特性

梁坤峰，王全海，阮春蕾，王 林

(河南科技大学a.车辆与动力工程学院;b.数学与统计学院;c.规划与建筑工程学院，河南洛阳471003)

0 引言

近年来，人们在结晶、流体力学和外界因素干预之间相互关联方面的认识取得了重大的进步，已开始积极寻找各种外界因素动态干预结晶过程与环境［1－5］。外加超声强化水或溶液结晶的研究越来越受到科研工作者的重视，虽然超声强化水或水溶液结晶的原因仍不十分清楚，但普遍认为超声作用于两相或多相体系产生的空化效应，即液体中存在或生成的气体微泡和空穴微泡，在超声场作用下振动、缩放和崩溃等一系列动力学过程促进了晶体的形成［4］。由于微气泡广泛存在于化工、动力设备、热能、医药等领域，对微气泡运动规律的研究对实际生产、流体力学及多相流动的发展具有重要意义。

目前，对气泡的上浮速度、气泡分布及超声应用等问题的研究已受到国内外学者广泛的关注。文献［6］测定了单个气泡在水及不同黏度甘油水溶液中的形变特性及上升终速度;文献［7］研究了气泡半径变化和上升运动的耦合影响，建立了运动方程，并用数值计算得出了气泡半径变化对上升运动的影响;文献［8］从力学平衡方程的角度，对气泡上浮过程中所受的各种主要力学影响因子进行了考虑，并详细讨论了黏滞系数与气泡运动阻力系数对气泡运动的重要影响;文献［9］研究了单个气泡在远程尾流中的运动特性及影响要素，重点考虑了上浮速度与传质速率相互影响的耦合因素。然而，上述研究在考虑气泡上浮过程中所受的主要力学影响因子，气泡半径变化对气泡上升运动特性影响以及外加超声场作用下微气泡运动特性等方面的研究尚不完善。

本文从力学平衡角度出发，建立了水中单个气泡的运动平衡方程，研究了各种力学影响因子对单个气泡上浮过程运动特性的影响;分析了不同粒径气泡时上浮速度的变化规律;进而重点探讨了气泡在外加超声波作用下，气泡粒径的变化规律以及气泡的运动特性。

1 模拟理论与方法

气泡运动过程由其受力情况决定，为了研究方便，做出以下假设:

(Ⅰ)气泡在运动过程中保持球形状态。

(Ⅱ)气泡内气体温度不变。

(Ⅲ)液体处于静止状态，无流动。

根据假设，分析气泡的各个受力，建立单个气泡运动平衡方程，如下:

其中，Fg为气泡的重力;Fb为气泡受到的浮力;Fd为运动黏性阻力;FA为虚拟质量力;FB为Basset 力［10］。

将各力的表达式代入平衡方程式(1)，经过整理化简可得:

由气泡运动微分方程式(2)可知:式中关于Basset 力的积分式包含一奇异端点，对其求解需要妥善处理该广义积分项。文献［11］基于广义积分的极限审敛法，判定该广义积分项必定收敛，提出小区间［t－△t］内近似公式，消除奇异点，直接由复化梯形公式求解积分项，如式(3)所示。

为提高数值计算结果的精度，采用先预测再校正的方法即改进的Eular 法［12－13］，通过自适应变步长联立求解方程。即当解的变化较慢时采用较大的计算步长，从而使计算速度加快;当方程的解变化较快时，积分步长适当变小，从而使得计算的精度提高。模型求解中，一些关键参数的取值如表1 所示。

表1 各参数取值

2 计算结果及分析

2.1 力学因子影响

图1 为气泡在力的影响下上浮运动速度随时间的变化曲线，由图1 可以看出:随着时间的增加速度逐渐增加，运动到某一时刻速度趋于稳定。在图1 中，曲线a 表示考虑虚拟质量力和Basset 力时的速度曲线，曲线b 表示不考虑Basset 力时的速度曲线，对比这两条曲线，发现不考虑Basset 力时，气泡运动速度比考虑Basset 力时速度大很多，表明Basset 力不仅持续影响气泡的运动，而且起主要作用。而在不考虑虚拟质量力和Basset 力及不考虑虚拟质量力时，气泡上浮过程的初始阶段，气泡能从零突变到稳态速度，不考虑Basset 力与不考虑虚拟质量力及Basset 力时的曲线在3 ms 时刻后基本重合，表明虚拟质量力及Basset 力对气泡的运动有影响。此外，为清晰展示初始阶段不考虑虚拟质量力和Basset 力及不考虑虚拟质量力时气泡上浮速度突变的规律，图2 给出了气泡上浮初始阶段各个力的影响曲线放大视图;由图2 可知:气泡运动初期，速度变化非常剧烈，具有显著的震荡特征，但很快趋于稳定，时间为0.01 ms，由此进一步表明虚拟质量力和Basset 力需要同时考虑。

图1 气泡上浮过程各个力的影响曲线

图2 气泡上浮初始阶段各个力的影响曲线

2.2 气泡粒径影响

图3 为粒径分别取30 μm、50 μm、100 μm、200 μm、300 μm 时，气泡上浮过程的速度随时间的变化曲线。由图3 可见:不同粒径，随着时间的增加气泡速度均呈递增趋势，且初始时刻速度增长较快，在气泡上浮过程后期其速度大小趋于稳定;同一时刻，气泡的粒径越大其上浮速度越大，反之，气泡的粒径越小其上浮速度越小;此外，当气泡粒径小于50 μm 时，随着时间的增加，气泡上浮速度增加趋势不明显。图3 曲线表明:气泡的上浮速度与气泡自身的粒径有直接关系，因为粒径大的气泡受到液体的浮力大，所以气泡运动速度就快，而对于粒径小的气泡，即气泡粒径小于50 μm 时，如要获得较大的速度，则须借助外力作用。

图3 定粒径气泡速度变化图

表2 为气泡粒径分别取30 μm、50 μm、100 μm、200 μm、300 μm 时，气泡运动末速度的实验值与模拟值的对比表。模拟值可以根据方程(3)计算得出，实验值则依据文献［4］可得，由表2 可以看出:实验值与模拟值的变化规律一致，即气泡的粒径越大其上浮速度越大，且气泡上浮过程中，模拟值与实验值误差均小于8.0%，表明本文所提出的求解方法可行。

2.3 超声波影响

当外加超声Pasin［2πf(t－x/c)］作用于气泡时，气泡受到激励声波的拉伸和压缩作用产生振动。假设液体是理想的、不可压缩的连续介质，黏滞系数为常数，并设激励声场频率和强度恒定，声波波长远大于空化气泡半径，气泡在运动中内部蒸汽压保持常数，与周围液体无热量交换，可由流体Navier-Stokes 方程、状态方程、无限处和气泡壁处的边界条件而建立RP 方程［14］。

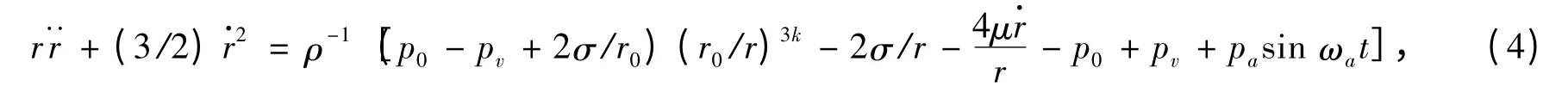
表2 实验与模拟结果对比

式中，r0为气泡初始半径;r 为气泡运动半径;ρ 为气泡外液体的密度;σ 为气泡外液体的表面张力;p0为气泡外大气压;pv为水蒸气压;pa为超声激励声压;μ 为液体的黏度系数;γ 为等压比热容与等容比热容的比值。各参数取值如表3 所示。

表3 参数取值

在超声波作用下，气泡既受重力、浮力、黏性阻力、虚拟质量力和Basset 力的影响，还会受到声压梯度力的作用，位于x 处声压梯度力可由式(5)计算［15］:

此时，气泡的运动平衡方程变为:

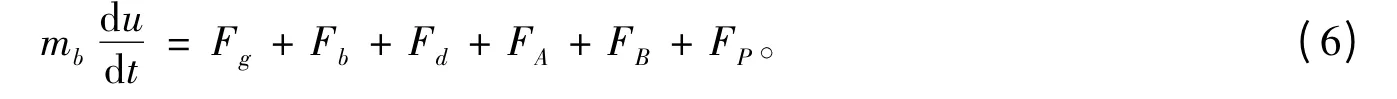
图4 为声波作用下气泡速度变化曲线。设初始时刻气泡处于超声波1/8 波长处，即x =1/8λ，采用Runge-Kutta 法数值求解方程(4)，得到气泡粒径随时间t 的变化关系，如图4a 所示，表明在超声波作用下气泡的粒径呈震荡波动变化。根据新的平衡方程式(6)，采用改进的Eular 法模拟求解，得到超声波作用下气泡上浮速度曲线，其结果如图4b 所示，其中，实线为考虑声压梯度力时气泡速度变化曲线，其纵坐标对应左侧的纵坐标;虚线为不考虑声压梯度力时气泡的速度变化曲线，其纵坐标对应右侧的纵坐标。由图4b 可知:超声波作用下，不考虑声压梯度力时，气泡速度变化整体上呈递增趋势，但其速度值量级较小;当考虑声压梯度力时，气泡速度呈近似正弦波动状态，且其振动的振幅逐渐增大，速度数量级比不考虑声压梯度力时的大很多;表明超声波作用下，气泡受到声压梯度力作用，并对气泡的运动产生很大的影响，研究气泡运动时必须考虑超声引起的声压梯度力。

图4 声波作用下气泡速度变化曲线

图5 为初始位置x=1/4λ、1/2λ、3/4λ、λ 时，气泡速度随时间变化的曲线图。由图5 可知:不同的初始位置x 处，其速度变化规律不同，其原因为在外加超声作用时，气泡受声压梯度力FP的大小、方向与气泡初始时刻的位置x 有关。对比x=1/4λ 与x=3/4λ 时的速度曲线可以看出:两条曲线是对称的，同样，x=1/2λ 与x=λ 时的速度曲线也是对称的，因为在x=1/4λ 与x=3/4λ 和x=1/2λ 与x=λ 处气泡受声压梯度力FP的方向相反;对比x =1/4λ 与x =1/2λ 时的速度曲线可见:x =1/4λ 时的速度峰值比x=1/2λ 时速度峰值略高，因为x=1/4λ 时的声压梯度力FP较大。

图6 为初始时刻x=1/4λ、1/2λ、3/4λ、λ 时，气泡上浮运动的位移随时间的变化曲线图。由图6 可见:气泡速度的波动变化引起气泡位移的波动;当x =1/4λ、1/2λ 时，运动后期气泡的位移向下，x =3/4λ、λ 时，运动后期气泡的位移向上;x=1/4λ 与x =3/4λ时，气泡的位移曲线对称，同样，在x =1/2λ与x=λ 时，气泡的位移曲线亦呈对称特征，均因其所受的声压梯度力FP的方向相反。

图5 气泡初始位置对速度的影响

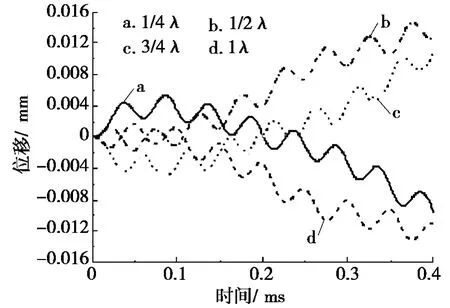
图6 气泡初始位置对位移的影响

3 结论

(1)静水中气泡的上浮速度随时间增加而逐渐增大，计算值与实验值具有很好的一致性。上浮初始阶段必须考虑由于加速度所引起的虚拟质量力和Basset 力对上浮速度的影响，且在不考虑虚拟质量力时，上浮速度具有震荡特征;气泡上浮后期，上浮速度趋于稳定;在所计算的气泡粒径范围(30 ～300 μm)内，气泡上浮速度从静止变化到稳定所经历的时间均在10 ms 量级。

(2)静水中气泡初始半径越大，气泡上浮速度越大，气泡初始粒径越小，气泡上浮速度越小，但达到稳定的时间越短;当气泡初始粒径小于50 μm 时，依靠气泡上浮的各种力学影响因子难以达到较大的上浮速度。

(3)声压梯度力对气泡运动的影响强于其他力学影响因子，速度相差两个数量级;气泡速度的变化与超声波发生规律一致，近似呈现正弦波动的变化规律，速度波动的振幅逐渐增大;气泡的初始位置处于超声波的不同波长处，气泡运动的方向相异，使得气泡具有上下两个方向的位移变化。

［1］ Yu D Y，Liu B L，Wang B C.The Effect of Ultrasonic Waves on the Nucleation of Pure Water and Degassed Water［J］.Ultrasonics Sonochemistry，2012，19(3):459－463.

［2］ Heneghan A F，Haymet A D J. Liquid-to-crystal Heterogeneous Nucleation Bubble Accelerated Nucleation of Pure Supercooled Water［J］.Chemical Physics Letters，2003，368(1/2):177－182.

［3］ Mathieu S，Roman P，Julien A. A Theoretical Model for Ice Primary Nucleation Induced by Acoustic Cavitation［J］.Ultrasonics Sonochemistry，2010，17(1):98－105.

［4］ Thomas L，Muthupandian A，Sandra K.The Fundamentals of Power Ultrasound:A Review［J］.Acoustics Australia，2011，39(2):54－63.

［5］ 李玉刚，王程远，陈卫锋，等.液－液雾化液滴的粒径分布特性［J］.河南科技大学学报:自然科学版，2010，31(3):29－32.

［6］ 郭容，蔡子琦，高正明.黏性流体中单气泡的运动特性［J］.高校化学工程学报，2009，23(6):916－921.

［7］ Chakraborty B B，Tuteja G S.Motion of an Expanding Spherical Gas Bubble in a Viscous Liquid Under Gravity［J］.Phys Fluids A，1993，5(8):1879－1882.

［8］ 石晟玮，王江安.水中微气泡上浮过程的力学影响因子研究［J］.海军工程大学学报，2008，6(3):83－87.

［9］ 田恒斗，金良安，王涌，等.考虑单气泡运动特性的舰船尾流气泡分布研究［J］.兵工学报，2011，9(9):1126－1131.

［10］ Zhang J，Fan L S.On the Rise Velocity of an Interactive Bubble in Liquids［M］.Chemical Engineering Journal，2003，92:169－176.

［11］ Carrica P M，Bonetto F J，Drew D A，et al.The Interaction of Background Ocean Air Bubbles with a Surface Ship［J］.Number Meth Fluids，1998，28(4):571－600.

［12］ 李庆扬，王能超，易大义.数值分析［M］.武汉:华中科技大学出版社，2002:88－90.

［13］ Chen M.An Automatic Recognition of the Best Threshold for Image［J］. Computer Applications and Software，2006，23(4):85－86.

［14］ Stride B E.The Influence of Surface Adsorption on Microbubble Dynamics［J］.Philos Trans A Math Phys Eng Sci，2008，366(1873):2013－2015.

［15］ 袁竹林，李伟力.细微颗粒在行波和驻波声场中运动特性数值实验［J］.东南大学学报，2005，35(1):140－144.