海水中电偶极子电场分布有限元分析

刁爱民，杨庆超，王杏青

(海军工程大学 a.科研部;b.电气与信息工程学院 电磁环境与防护系，武汉 430033)

海水中电偶极子的电磁场是目前水下通讯和水下目标探测方面的研究重点。电偶极子是指由离开一定距离的电量相同、符号相反的两个点电荷组成的系统，两个点电荷之间的距离与待求场点到他们中心的距离相比很小，是最简单也是最基本的一种电磁场场源，求解电偶极子产生的电场也就可计算出任意场点的电场值。

海水是一种导电媒质，当海水的深度较大时，假定海水的电导率恒定不变，可将海水看作无限大导体空间，并利用有限元方法对感兴趣的区域进行有限分割，选取适当的插值函数，就可近似推导电场的解析表达式。当海水深度较小时，可将深海等效为空气-海水两层模型。

1 计算模型

1.1 深海点电荷模型［1］

将海水的电导率视为恒定不变，如图1 所示，电荷量为Q 的点电荷的电场公式为:

用一个半径为r 的实心等势铁球体代替点电荷，若在球体上加上均匀的固定电势φ0，则由高斯定律可得:

取另一半径为R 的高斯面，由高斯定理得:

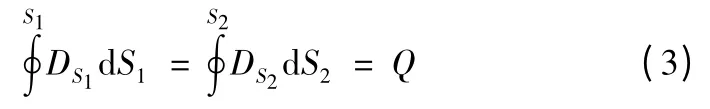
由E=εD，可得即电势为φ0，半径为r 的等势球体与带电量为Q=4πεrφ0的点电荷产生的远场一样，可以相互代替。即深海点电荷模型可以是一个等势小球。

图1 点电荷模型

2 深海中电偶极子有限元模型

由点电荷模型可知，可用2 个实心等势铁球体来代替点电荷构建一个电偶极子模型，如图2 所示。由于电偶极子是指由相距很小距离的电量相同，符号相反的2 个点电荷组成的系统，故应满足2 个条件:①小球的半径比二者之间的距离至少小1 个数量级;②求解的范围比二者之间的距离至少高1 个数量级。即该模型中电场源为2 个电势相反的球体，求解域为充分大的充满海水的立方体，边界条件为自然边界条件。

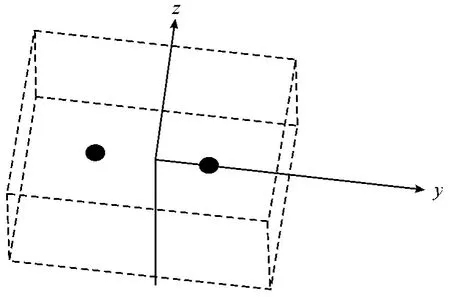
图2 电偶极子有限元模型

2 电偶极子电场的微分方程和边界条件［2］

2.1 深海电偶极子有限元模型

式中:φ 表示介质中以及金属表面的电位值;φ0是边界上电位的给定值，该模型中边界的电位为0。

2.2 空气-海水两层有限元模型［3］

当空间分成如图3 所示的2 个平面，其中一半充满空气，另一半为不流动的海水，空气为区域1，海水为区域2。以空气-海水界面为z =0 的平面，空气占据z ＞0 的上半空间，而海水则占据下半空间，空气的电磁特性为常数ε0、μ0和σ0(σ0=0)，假定海水的电磁特性为常数ε、μ0和σ，则两部分介质中的传播常数分别为:

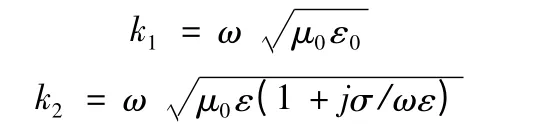
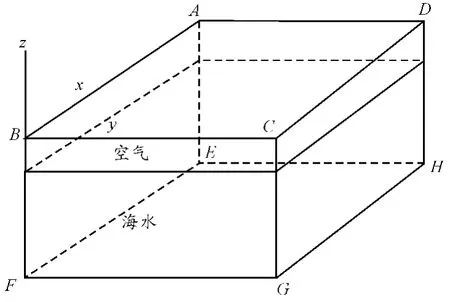
图3 空气—海水两层模型

假设在海水中有一电流源J，取时谐因子为ejωt，则电场波动方及边界条件为［4］:

选取一个足够大的六面体区域包围电流源J，则在六面体的外边界上，电磁场的边界条件是:

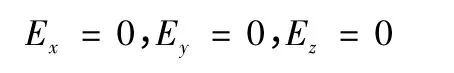
3 有限元方程的求解

应用广义变分原理，对于研究的电磁场方程及对应的边界条件的变分为［5］:

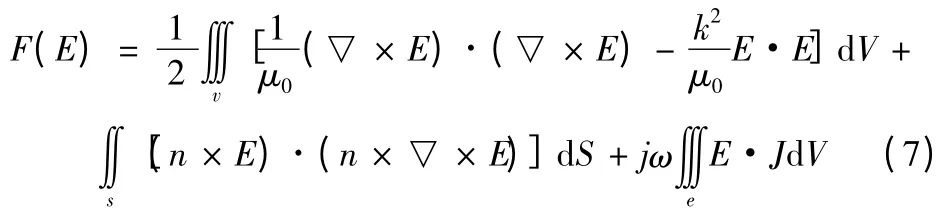
采用的基本单元是六面体单元，并采用了与常规有限元不同的网格剖分技术。具体方法是将场域划分成若干个网曲面，每个曲面层由若干个六面体单元组成。由于在海水平面剖分单元的密度要求高，而在所取区域上部空气中和深部单元的密度要求低，因而在实际剖分时对于空气中和不同深度海水中的曲面层是永不等距的网格剖分，分别采用向上收缩网格和向下收缩网格的方法，大大地减少了单元和节点数。经求导，并整理，综合后得总刚度矩阵K:

式中:K 为n×n 方阵;b 为1 ×n 列阵;n 为剖分节点数。

将其代入式(8)即可求得垂直电偶极子的电场有限元方程组。

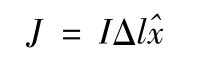
将其代入式(8)即可求得水平电偶极子的电场有限元方程组。

对于式(8)的有限元方程，可通过多种解方程组的方法进行求解，直接解法中有LU 分解、Gasuss 法和带状矩阵算法等;迭代法有共轭梯度法和复双共轭梯度法。当线性方程组系数矩阵的条件数较差时，LU 分解方法最为稳定。如果系数矩阵中将散度效正项考虑进去，则方程组的系数矩阵变为不对称，系数矩阵需要存储满阵，这样就很难满足三维电磁问题的求解。复双共轭梯度法收敛速度快，适用于大型稀疏对称矩阵，采用一维压缩内存存储方法，在计算机上可实现三维电磁问题的求解。

4 误差分析

在深海模型中，海水的介电常数为81，球体半径为0.1 mm，两球间距离l=10 mm，球表面的电位为φ0= ±105V，则该模型等效于一个电荷量q=320π(C)，距离l=10 mm 的电偶极子产生的场［6］。

用Matlab 计算得到该电偶极子的场如图4 所示。

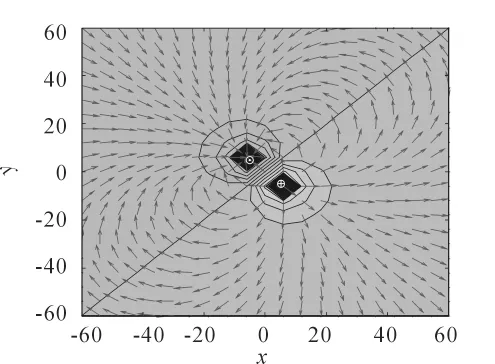
图4 电偶极子电势分布

穿过电偶极子的对角线上的电场分布如图5 所示。

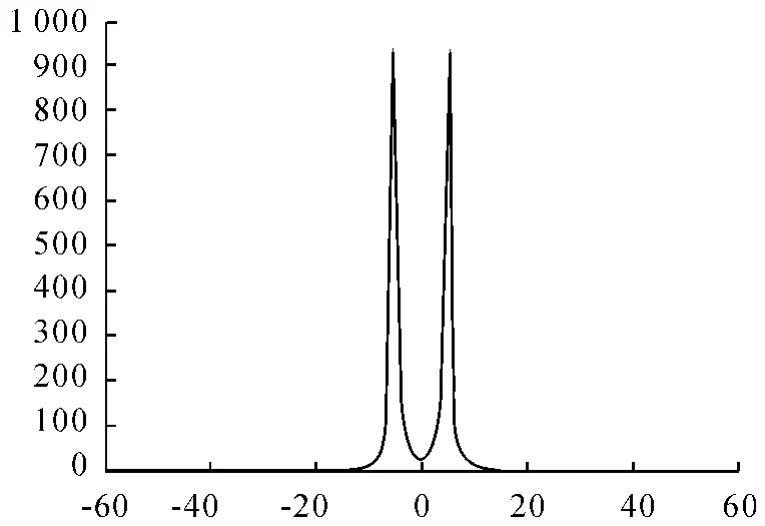
图5 电偶极子对角线上的电场分布

有限元法求得的两小球的产生的电场分布如图6所示［7］。

图6 ansoft 仿真电偶极子的电场分布

将二者对角线的(-3，3)部分的电场分布进行比较，结果如图7 所示，有限元的计算结果变化较为平缓，误差较大，原因是小球的半径再小也不能近似为零，所以近场的误差较大，符合实际。结果表明小球的曲率越大，附近的电场也就越大，计算结果也会更加陡峭，跟理论的结果更相近，但对剖分精度的要求加大，同时增加了计算量。

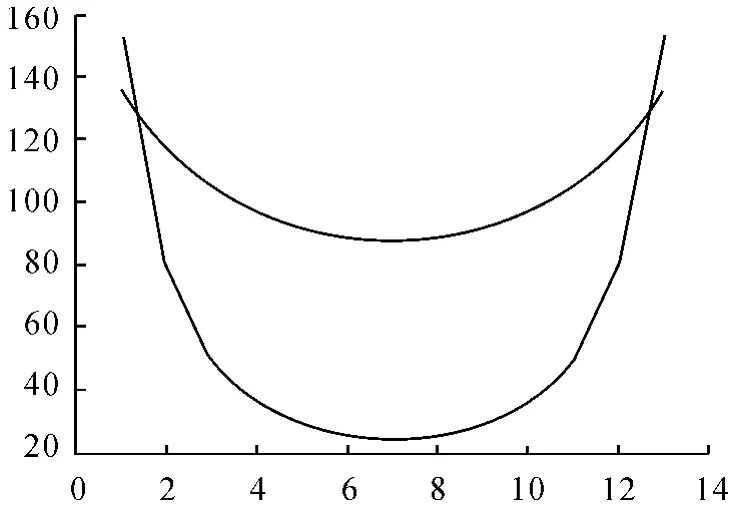
图7 对角线上(-3，3)部分的电场分布比较

将二者对角线(-60，-8)部分的电场分布进行比较，如图8 所示，结果表明二者几乎重合，表明小球的电偶极子模型的远场效果很好，同时对小球的半径的数量级要求不高，较为容易实现。

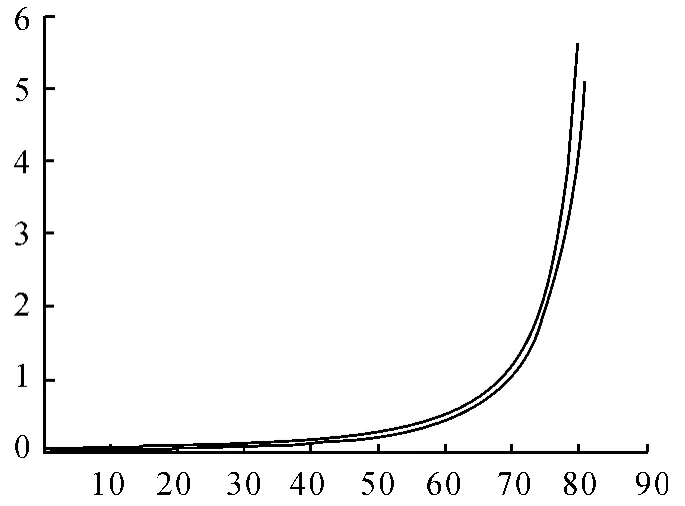
图8 对角线上(-60，-8)部分的电场分布比较

5 结束语

本文利用高斯定律从理论上分析了等势小球和点电荷的电场分布的一致性，同时利用有限元方法推导出了海水中静态和时谐电偶极子的电场有限元方程，通过对有限元方程的求解计算得到海水中任意场点的电场值。同时利用Matlab 建立的电偶极子模型比较、分析了静态电偶极子模型的误差，结果表明有限元电偶极子模型具有很好的远场效果。可见，运用文中提出的模型在深海区域对电场偶极子进行分析是可行的。

［1］威廉·H·海特，约翰·A·巴克.工程电磁场［M］.西安:西安交通大学出版社，2009.

［2］倪光正，杨仕友，钱秀英，等.工程电磁场数值计算［M］.北京:机械工业出版社，2006.

［3］Kasper C，April M G.Electroglalvanic Finite Element Analysis of Partially Protected Marine Structures［M］.CORROSION/82，Huaston，TX:NACE，1982:168.

［4］黄临平，戴世坤.复杂条件下3D 电磁场有限元计算方法［J］.武汉:中国地质大学学报，2002，17(4):373-377.

［5］刘胜道，龚沈光.并矢格林函数法求解海水中电偶极子电场［J］.电波科学学报，2002.

［6］LI Yong，LIN Pin rong，XU Bao li，et al.Computing the electromagnetic response of the time-harmonic horizontal electric dipole in a homog-enous half-space under ionosphere coupling［C］//China:Computing Techniques for Geophysical and Geochemical Exploration，2008.

［7］赵博，张洪亮.Ansoft12 在工程电磁场中的应用［M］.北京:中国水利水电出版社，2011.