考虑振动模态耦合的结构声振特性
高晟耀,王德石,代仁文
(海军工程大学 兵器新技术应用研究所,武汉 430033)
板是广泛应用于舰船、航空、车辆、土木等工程领域的基本结构单元,获得其声学特征量解析解,对掌握结构辐射噪声控制机理具有普遍的意义。结构声振耦合问题的模态分析中,辐射阻抗表示结构振动和辐射声场之间相互作用,成为评价振动结构声辐射性能前提和关键,尤其是结构向重流体中辐射时,需要快速、精确地计算模态辐射阻抗。比较代表性的是将结构表面划分网格,利用波数近似以及傅氏变换的方法求得单元辐射阻抗并求和[1],然而稠密单元网格带来巨大计算量的同时,严重制约了频率分析范围。而且,各阶振动模态对结构声学量的贡献并不相互独立[2-4]。由此需要改进辐射阻抗计算方法,进一步研究考虑振动模态耦合的结构声振特性。在文献[5 -7]的基础上,本文采用坐标变换和级数逼近的方法,推导任意频率下简支板结构的模态辐射阻抗,研究其声辐射特性随振动模态耦合的变化规律,为噪声控制提供技术基础。
1 板结构声辐射模型
为利用经典的板结构振动和声辐射理论,获得结构辐射噪声控制机理,首先建立结构的声辐射模型,分析板结构辐射噪声产生原因及其组成。考虑嵌在无限障板中的矩形平板,以角频率ω 作简谐振动,法向振动速度为v (x,y ) 。假设平板位于z=0 平面,向无穷大空间辐射声波,选取空间中任意一点A( x,y,z ) ,B( x,y ) 为平板上的点,声场介质密度为ρ,声速为c,如图1 所示。
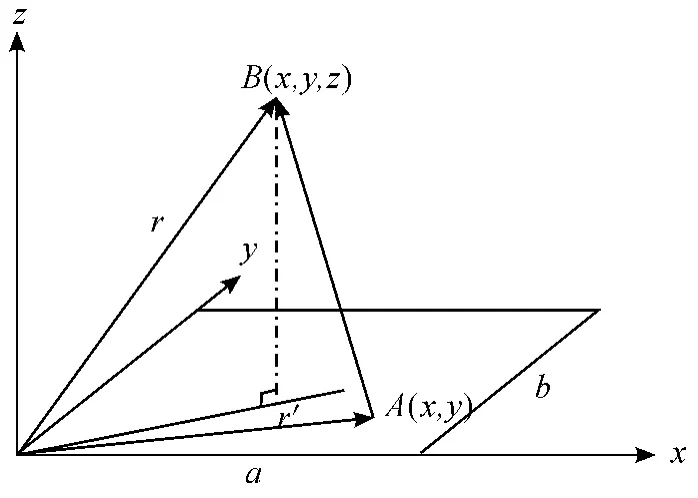
图1 嵌在无限障板中矩形板
由根据瑞利积分公式,声场中任意一点r (x,y,z) 的声压
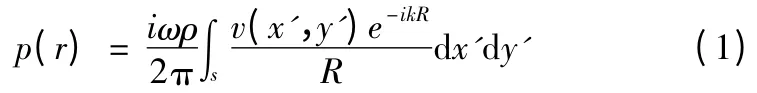

表示成矩阵形式

式(3)中,umn为模态振速幅值,ψmn振型函数。利用结构振动表面处的声强积分,可以得到板结构辐射声功率:
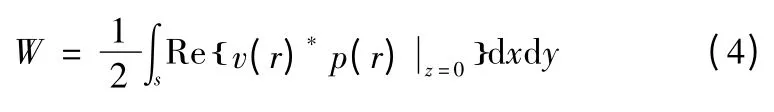
将式(1)和(2)代入方程(4),则

式(5)中,R 为声辐射阻即声功率传递矩阵,其第项元素:
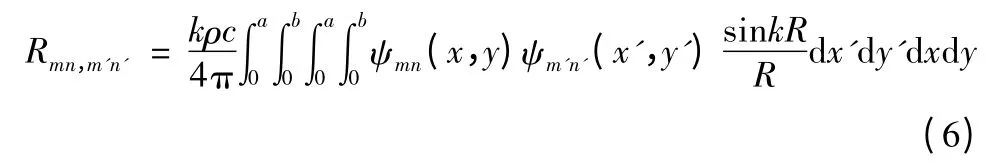
由声场互易性原理知,辐射阻矩阵是对称矩阵,其对角线元素对应自辐射阻,表示第(m,n)阶振动模态对声功率贡献,非对角线项对应互辐射阻抗,表示第(m,n)与(m',n')阶模态之间的耦合对声功率贡献。
为研究结构振动模态耦合对辐射声功率的影响,将其记:
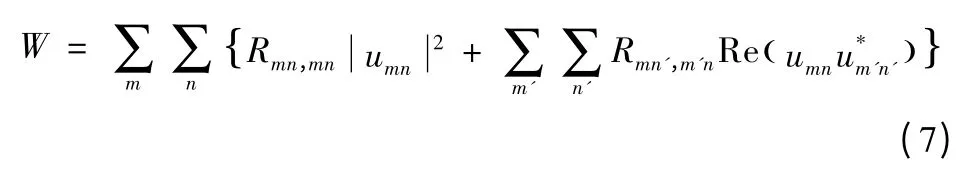
可知声功率由两部分组成,其一是各阶振动模态自身产生的自辐射声功率,即
借助于计算机信息技术所构成的银行系统数据库,其能够促使银行的管理效率得到大幅度的提升,从而在一定层面上提高该银行的竞争能力。就工商银行为例进行分析,其是我国最早应用计算机信息技术构建强大数据库的银行。在银行系统数据库构建完成之后,工商银行能够在银行的数据管理工作以及业务管理过程中进行信息计划管理技术的合理应用,进而实现银行整体信息化管理的雏形。借助于银行系统数据库的构建,还帮助工商银行实现了集中化的管理模式,促使该银行的管理水平得到大幅度的提升。

是正定矩阵,其特征值恒为正,则对角线元素Rmn,mn>0,对于任意的模态振动速度umn≠0 恒有Wmn,mn>0,故各阶模态的自辐射声功率将增强结构的总辐射功率。
其二是,声场使得振动模态发生耦合,模态耦合产生互辐射声功率。将第与阶模态振速表示为,则
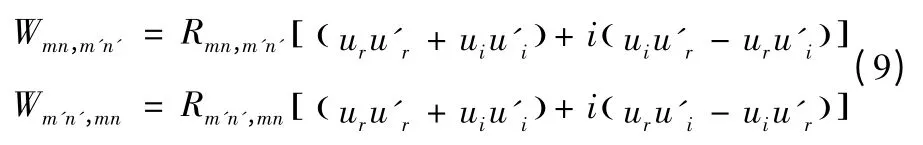
可以看出,和虚部相抵消,互辐射声功率:
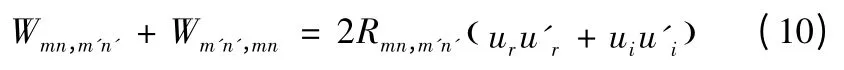
式(10)中,互辐射阻Rmn,m'n'是结构的固有属性,它与结构的材料、尺寸、形状、以及边界条件与激励频率等因素有关,而uru'r+uiu'还与激励力位置和相位相关。因此,结构振动模态间的耦合对辐射声功率的影响存在不确定性,需要进一步从模态分析的角度比较自辐射阻抗与互辐射阻抗下的声学特征量。
结构辐射效率是衡量结构声辐射能力的重要指标,定义

根据式(8)、(10)和(11),求得第(m,n)阶结构振动模态的自辐射效率
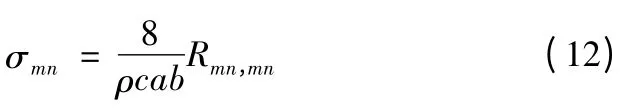

2 模态辐射阻推导
研究典型的简支板模型,对不同边界和形状辐射体的声振特性分析具有参考价值。简支板的振型函数ψmn表示:
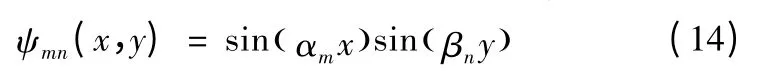
式(14)中,αm=mπ/a,βm=nπ/b。
由于模态辐射阻表达式是四重积分,直接计算比较困难,需运用坐标变换化简为二重积分。即令ε =x -x',ν =y-y',η=x+x',τ=y+y'。根据模态数m 与m'、n 与n'的关系,得到
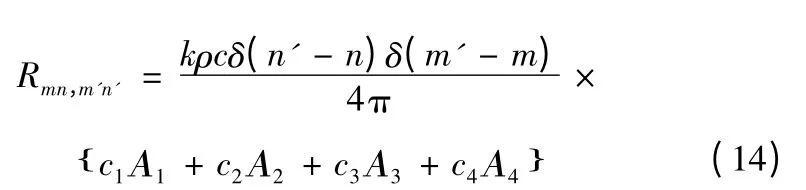
式(14)中
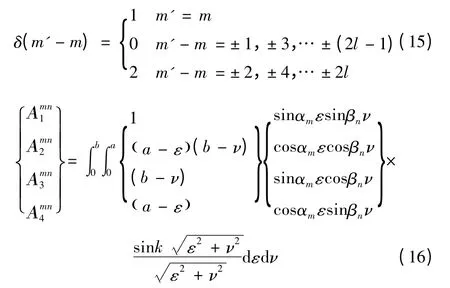
1)在中低频情况下,考虑到解析解式(16)的积分实现,对应用麦克劳林级数,并结合函数幂级数展开式,可以得到辐射阻矩阵简化后的解析式:
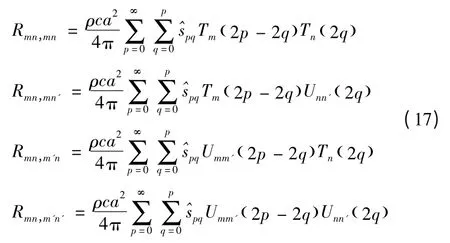
其中

2)在高频情况下,波数增大时,式(18)需要足够多的级数展开项才能保证其截断误差,为此sin(mπε)和cos(mπε)需用其泰勒级数展开替代,得到一组Bm(2p)和Tm( 2p )的修正式:
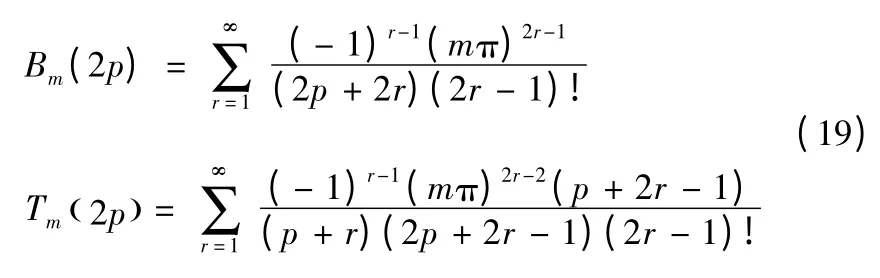
3 案例分析
选取四边简支的薄板,其几何尺寸为1 m ×0.75 m ×0.003 m,材料密度ρ =7 800 kg/m3,泊松比υ =0.3,弹性模量E=2.1 ×e11N/m2,模态阻尼因子η=0.01,空气密度ρ0=1.21 kg/m3,声速c=343 m/s。
3.1 模态辐射阻抗变化规律
从图2 中可以看出,变化趋势上,模态自辐射阻随波数增大而变大,达到峰值后逐渐趋于1,模态互辐射阻与其相比较小,在本征频率附近出现较大起伏振荡后趋于0;取值上,自辐射模态阻恒为正,而模态耦合项可能为负,低阶模态间的辐射阻明显大于高阶模态间辐射阻,并随着波数增加,各振动模态之间的耦合项减弱,即在高频段,振动结构的辐射声功率无需考虑模态之间的耦合作用。
图3为不同纵横比下模态自辐射和互辐射阻随波数变化曲线。图(a)表明,随着纵横比的减小,自辐射阻的驼峰增宽并向较高波数偏移;图(b)利用第1 阶模态的自辐射阻对互辐射阻作归一化处理,可看出,两较宽薄板自辐射阻最大值出现在ka=0 处,矩形板变窄时,互辐射阻抗的峰值向高波数偏移,印证模态耦合在低频段对方板的辐射特性影响显著。以上两图反映了结构振动向声能的转化能力与振动面的几何特征相关。
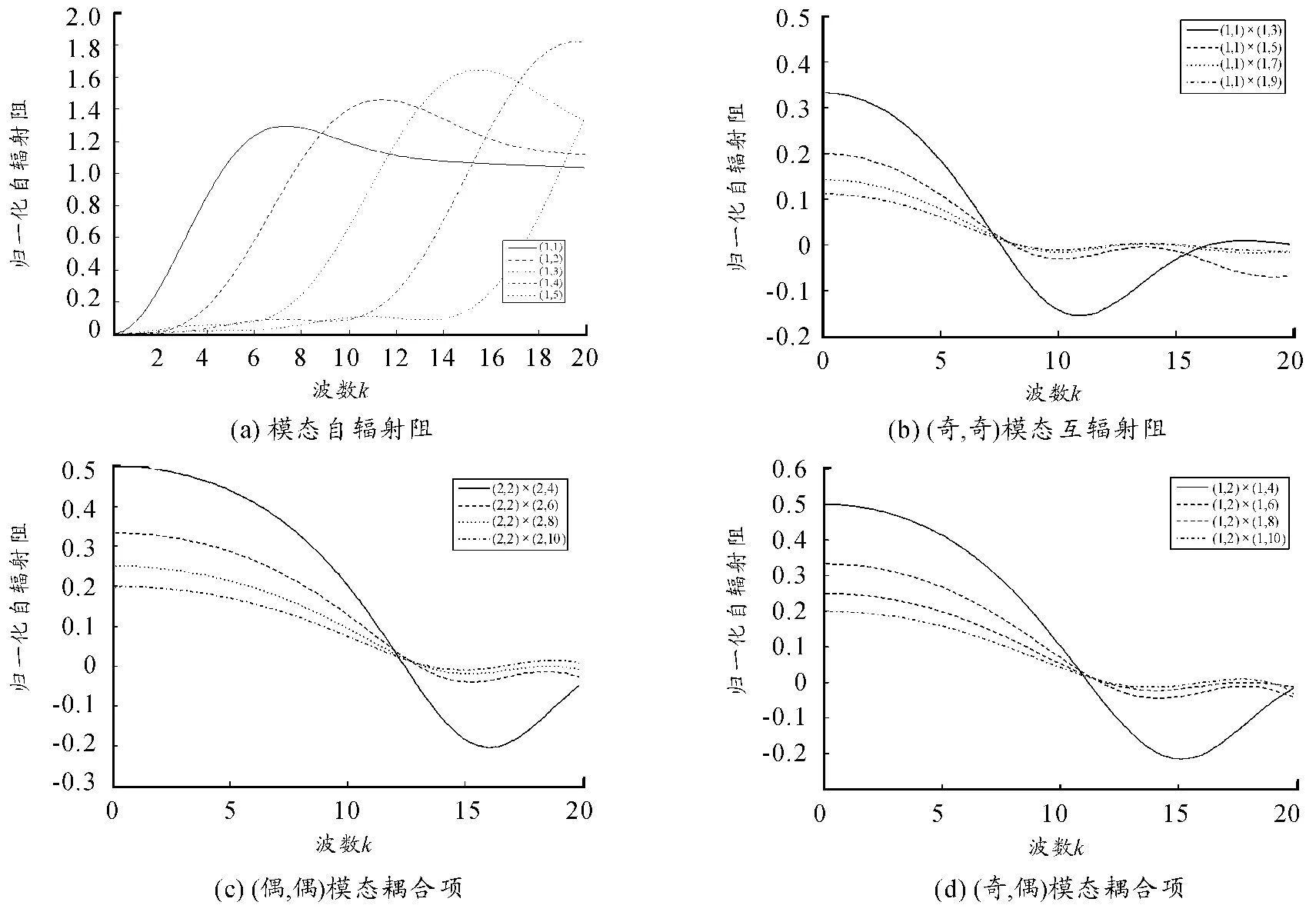
图2 模态自辐射与互辐射阻
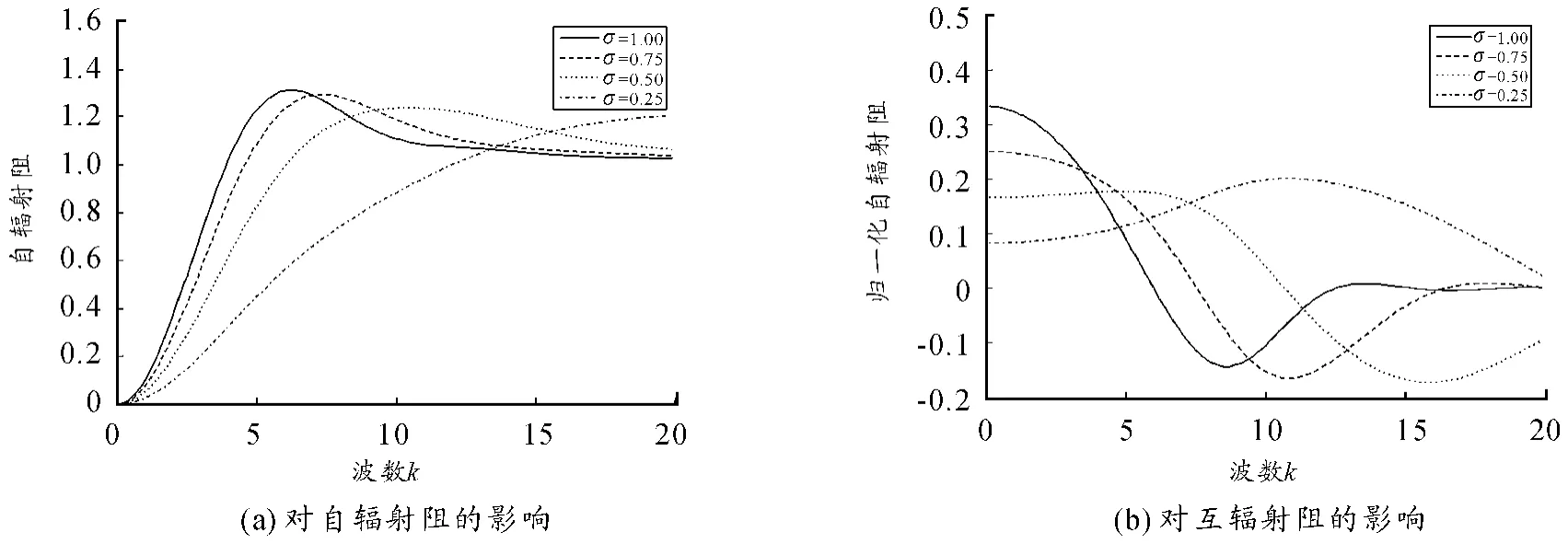
图3 纵横比对辐射阻影响
3.2 振动模态耦合对声辐射特性影响
考虑简支薄板在位置(x0,y0)处受集中简谐力Fsin(ωt)的激励,模态分析理论知其(m,n)阶模态速度表达式
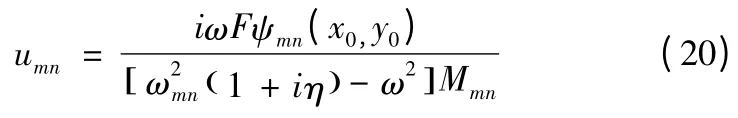
式(20)中,η 为阻尼损耗因子,模态质量 Mmn=板的固有频率弯曲刚度B=Eh3/12 ( 1 -υ2)。
结构模态辐射效率反映了简支板不同模态所辐射声功率能力的大小。对应(1,1),(2,1),(3,1),(1,2)模态自辐射效率为σ11,σ22,σ33,σ44,(1,1)阶模态与(3,1)阶模态的互辐射效率为σ14,(2,1)阶模态与(2,3)阶模态的互辐射效率为σ28,计算结果如图所4 所示。
由图4 看出,低频时的各阶模态自辐射模态效率有较大差异,模态阶数越高,其辐射效率越小。对于同一阶振动模态,频率越高,波长越短,辐射效率愈大。(奇,奇)模态的自辐射效率最高,(偶,奇)或(奇,偶)模态次之,(偶,偶)模态的自辐射效率最低。随着波数的增大,各阶振动模态的自辐射效率逐渐提高,最终趋向于1。对于振动模态的耦合,低频时,模态(1,1)和(1,3)的互辐射效率仅(1,1)低于阶模态的自辐射效率。高频时,各阶模态的自辐射频率均大于其互辐射频率,表明结构(奇,奇)振动模态低频时有较强耦合作用,高频时这种耦合相对振动模态自身的辐射声功率能力较弱。
为考虑结构振动模态耦合对辐射声功率的影响,分别在矩形板(0.25 m,0.187 5 m)和(0.5 m,0.35 m)处施加单位大小的简谐激励力时,结构(偶,奇)振动模态(2,1)和(2,3)之间耦合项对应的取值符号sign(w21,23),如图5 所示。从图中可以看出,振动模态间的耦合对辐射声功率的影响与激励频率和激励位置有关。在某段频率内,耦合项对辐射声功率的贡献可能为负,如果适当调整模态振速的相位,式(10)第2 项与第1 项抵消,可以降低振动结构的辐射声功率,正是结构有源噪声控制的机理,即在不改变系统的能量输入和耗散的情况下,重置结构表面振速分布,使其成为弱辐射体[8]。
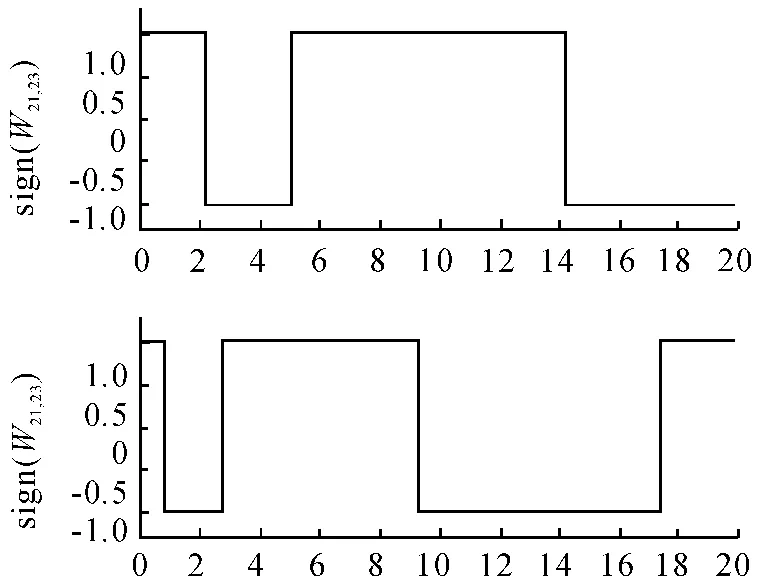
图5 不同激励位置的模态耦合项取值符号
图6给出了激励力作用在第一个位置时考虑模态间耦合和不考虑模态间的耦合的辐射声功率曲线。两条曲线基本吻合,模态耦合对辐射声功率的影响较小,仅在局部小幅改变曲线的数值,此算例中的耦合作用可以忽略不计。所以,抑制表面模态振速幅值,可减小结构的辐射声功率,达到控制噪声的目的。模态耦合项与结构材料、尺寸、形状、边界条件以及激励频率、位置和相位等因素都有关系,虽然难以给出是否考虑模态耦合项的具体准则,但可看出它对结构声振特性影响的程度较小。
取前1、2、4、6 阶模态时的辐射声功率,如图7 所示,可以看出,在分析频段内选取较少数目的低阶振动模态可以保证辐射声功率的计算精度。从侧面反映了,若在该频段进行结构噪声的控制,仅对前n 阶振动模态加以控制,便可显著降低结构的辐射声功率。结构发生共振时,共振结构模态对结构振动响应贡献最大,需对此共振模态予以控制。
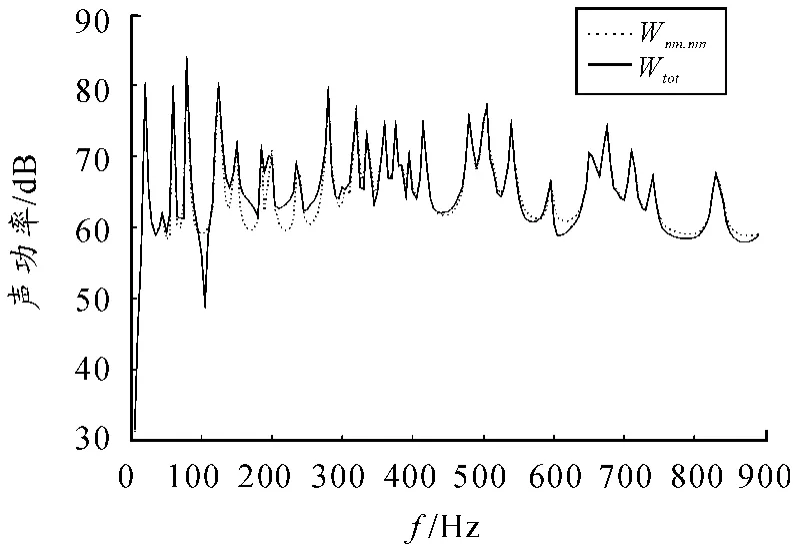
图6 考虑模态耦合和不考虑模态耦合的辐射声功率
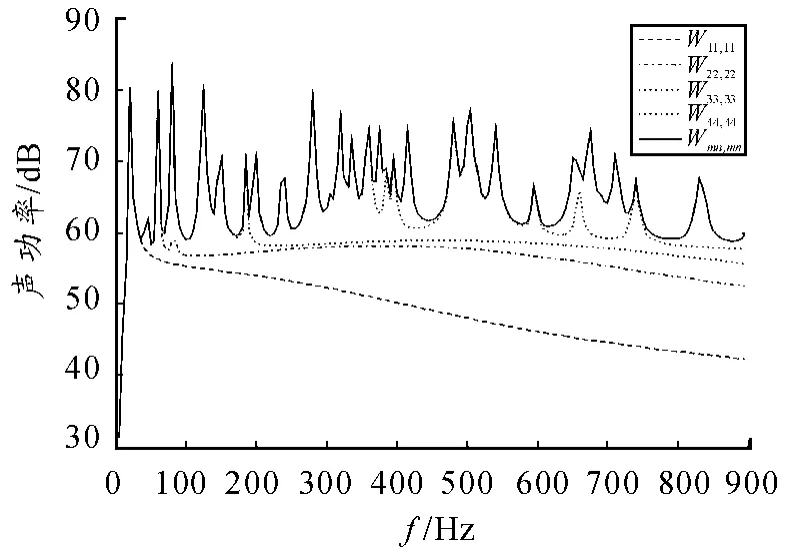
图7 结构各阶振动模态对声功率贡献
4 结束语
上述研究表明,采用坐标变换和级数逼近的方法计算模态辐射阻抗计算方法是准确有效的,可用于任意频率范围的结构振动和声辐射研究。振动模态耦合与结构几何和物理参数、边界条件以及激励频率、位置和相位等因素有关,在不改变系统的能量输入和耗散的情况下,可通过重置结构表面振速分布的方式使其成为弱辐射体,并给出了改变振动时空分布的基本原则和方法,为噪声控制提供了技术基础。
[1]SHA K,YANG J,GAN W S.A simple calculation methdod for the self-and mutual-radiation impedance of flexible rectangular patches in a rigid infinite baffle[J]. Journal of Sound and Vibration,2005,282:179-195.
[2]沈苏,刘碧龙,李晓东,等.简支矩形板模态辐射抗的一种快速计算方法[J].声学学报,2010,35(2):126-133.
[3]黎胜,赵德有.结构声辐射的振动模态分析和声辐射模态分析研究[J].声学学报,2004,29(3):200-208.
[4]SYDER S,TANAKA N. Calculating total acoustic power output using modal radiation efficiencies[J].Journal of the Acoustical Society of America,1995,97:1702-1709.
[5]Li W L,Gibeling H J.Determination of the mutual radiation resistances of a rectangular plate and their impact on the radiated sound power[J]. Journal of Sound and Vibration,2000,229(5):1213-1233.
[6]Li W L.An analytical solution for self- and mutual radiation resistances of a rectangular plate[J].Journal of Sound and Vibration,2001,245(1):1-16.
[7]GRAHAM W R.Analytical approximations for the model acoustic impedance of simply supported rectangular plates[J].Journal of the Acoustical Society of America,2007,122(2):719-729.
[8]KOOPMANN G H,Belegundu A D.Tuning a wine glass via material tailoring-an application of a method for optimal acoustic design[J]. Journal of Sound and Vibration,2001,239(4):665-678.

