一类具有常数移民和分布时滞的SIRS传染病模型分析

朱春娟

（广东韶关学院数学与信息科学学院，韶关 512005）

一类具有常数移民和分布时滞的SIRS传染病模型分析

朱春娟

（广东韶关学院数学与信息科学学院，韶关 512005）

通过恰当的Liapunov函数，研究了一类在易感者类和移出者类具有常数移民、通过媒介传播和含分布时滞的SIRS传染病模型.在不存在染病者移民时，得到了地方平衡点存在的阈值R0.当R0＜1时，无病平衡点是全局渐近稳定的；当R0＞1时，无病平衡点不稳定，地方平衡点全局渐近稳定.在染病者存在常数输入时，模型不存在无病平衡点，地方平衡点全局渐近稳定.

传染病模型；分布时滞；平衡点；稳定性

一般讨论的传染病模型，染病者类都没有常数移民，但对某些疾病，除易感者具有常数移民率外，染病者及移出者也有常数移民，如爱滋病、非典等，尽管各国海关进行控制，但仍然有少量的带病者进入某一地区，使疾病在这一地区流行.关于传染者也具有常数移民率的传染病模型，目前所见的文章还很少，主要有陈军杰.李建全等［1-2］.

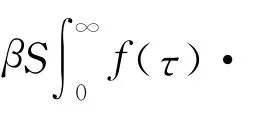
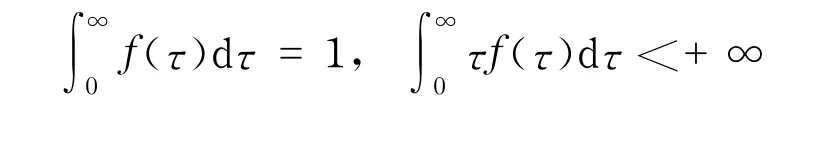
1 模型的建立

研究系统

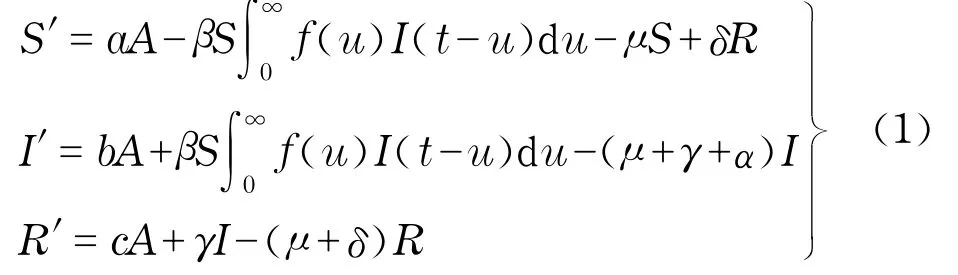
总人口方程为

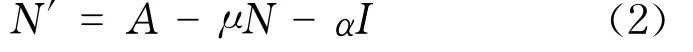
式中，N=N（t）表示t时刻总人口；A为单位时间从外界迁入的总人口；a＞0，b≥0，c≥0，a+b+ c=1，a，b，c分别为输入人群中易感者S、染病者I和移出者R所占的比例；γ，δ，μ，α分别为染病者成为移出类的恢复率、免疫失去率、出生（死亡）率、因病死亡率.其中，β，γ，μ，α均为正常数，δ为非负常数.假设新生儿均为易感者.

由于N=S+I+R，并结合式（2），系统（1）等价于系统

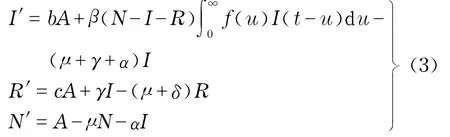
当b=0时，系统（3）有无病平衡点；当b＞0时，没有无病平衡点.分b=0和b＞0两种情形进行研究.

2 平衡点的稳定性

现分两种情形进行研究.

情形1 b=0.

则系统（3）等价为

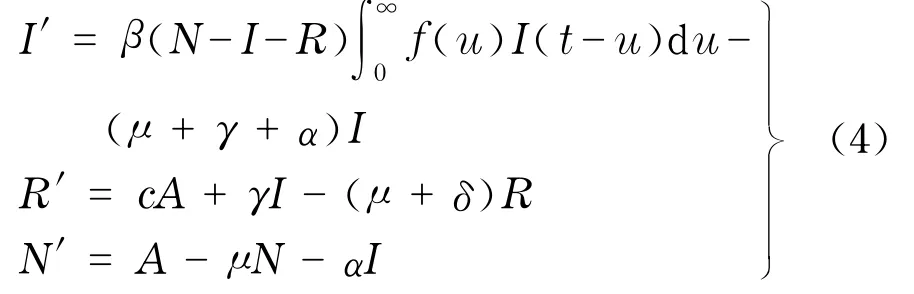
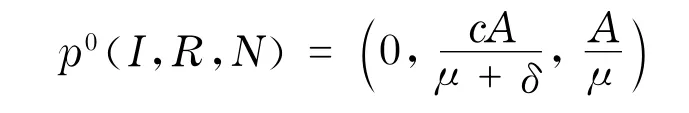
记

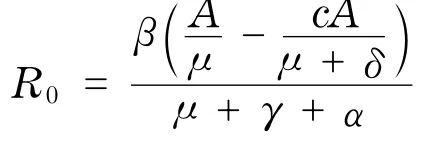
由系统（4）的后两个方程解出

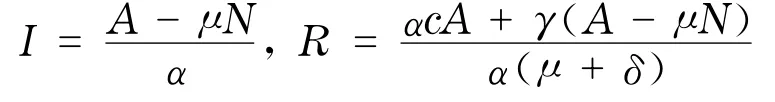
将I和R代入系统（4）的第一个方程，得

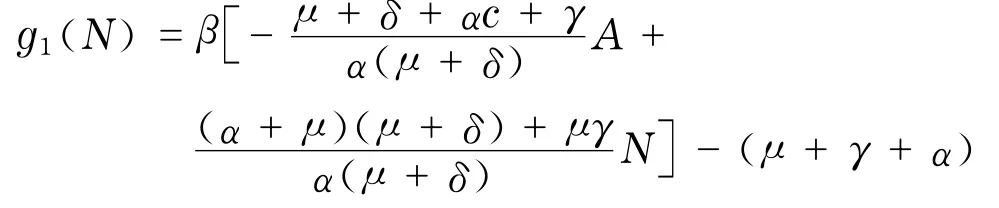
显然，g1（0）＜0，

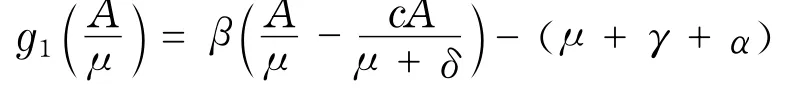
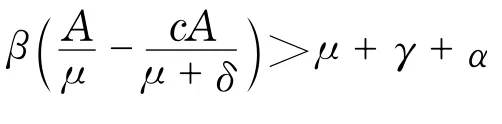
定理1 记

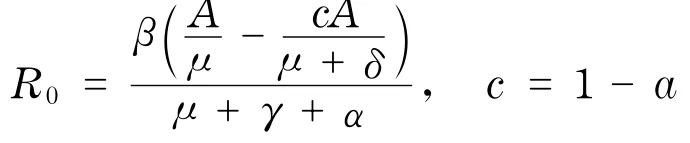
系统（4）始终存在无病平衡点

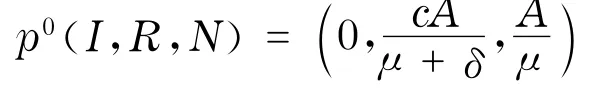
当R0＞1时，系统（4）存在唯一地方病平衡点p*（I*，R*，N*）.

2.1 无病平衡点p0的全局渐近稳定性

定理2 对于系统（4），当R0＜1时，无病平衡点p0是全局渐近稳定的；当R0＞1时，p0是不稳定的.

证明 容易得到系统（4）对应于平衡点p0的线性化系统为

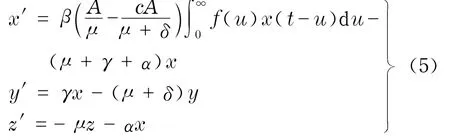
将x=c1eλt，y=c2eλt，z=c3eλt代入式（5），得到对应于平衡点的特征方程为

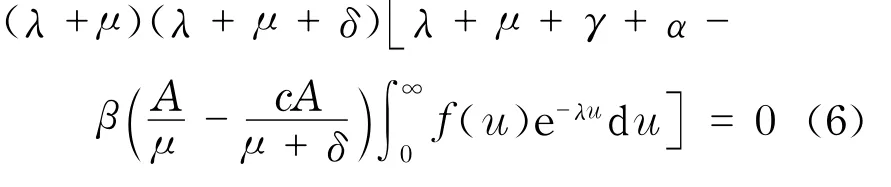
方程（6）除有根λ=-μ，λ=-（μ+δ）外，其余的根由方程

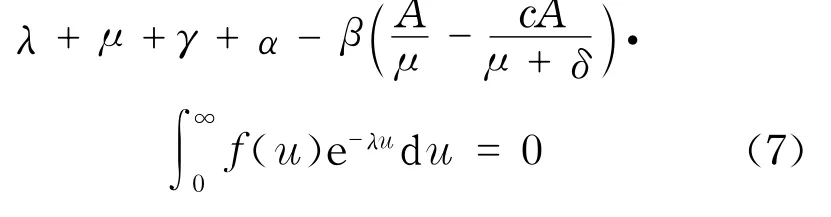
来决定.

设方程（7）有根λ=m+n i，其中，m≥0，则将λ=m+n i代入式（7），比较两端实部，得

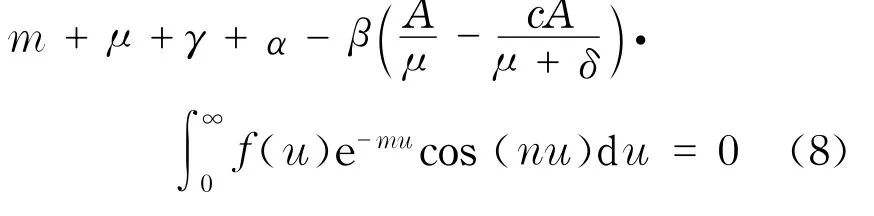
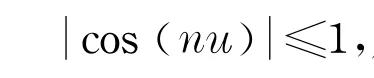
设

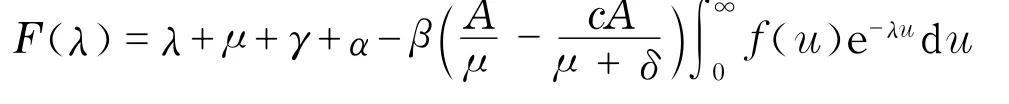
当R0＞1时，即

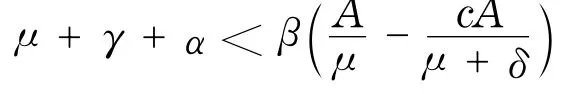
考虑Liapunov函数

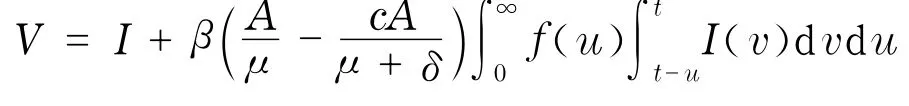
则

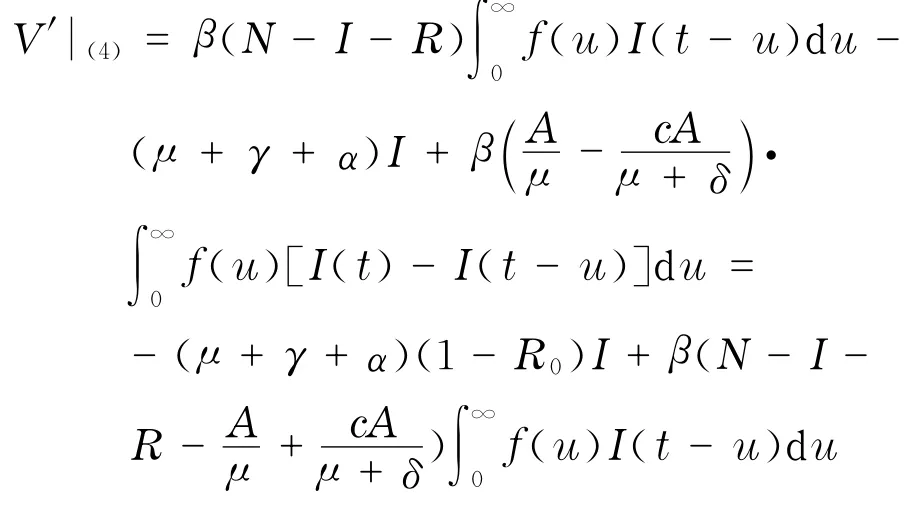
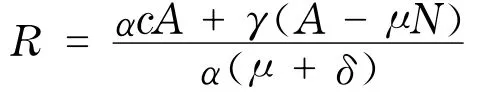
2.2 地方平衡点p*的全局渐近稳定性

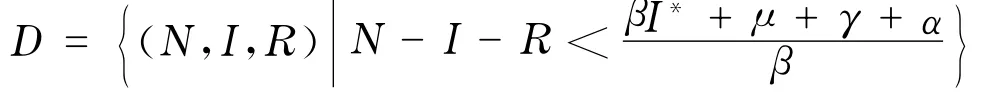
证明 系统（4）在p*处的线性化系统为

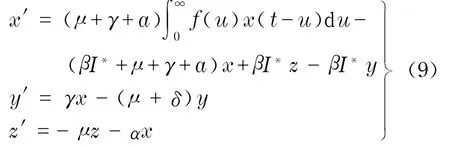
类似于前面的推导，地方平衡点p*是局部渐近稳定的.

对系统（4）作变换

x=I-I*，y=R-R*，z=N-N*

则式（4）变为

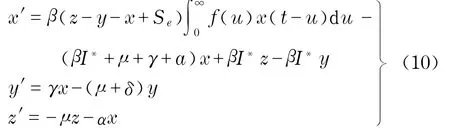
其中，Se=N*-I*-R*.

考虑Liapunov函数

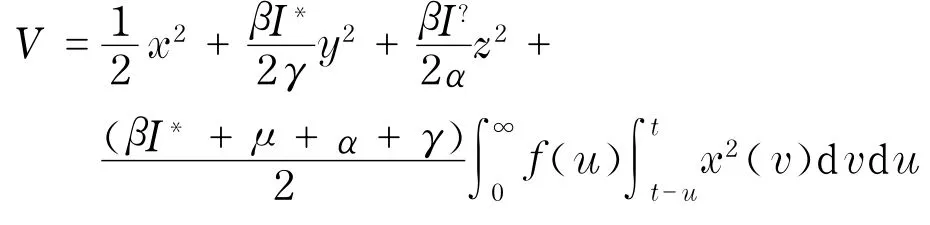
则

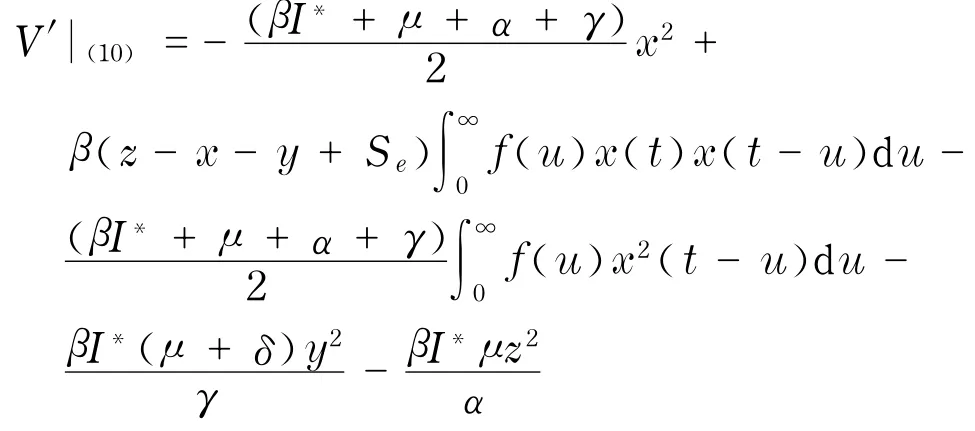
记

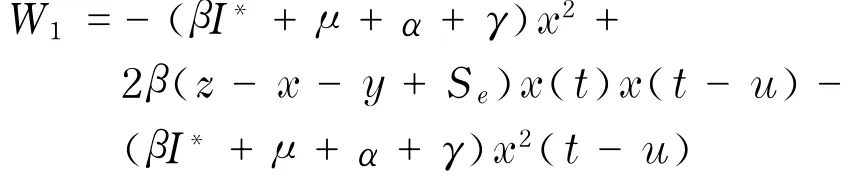
则

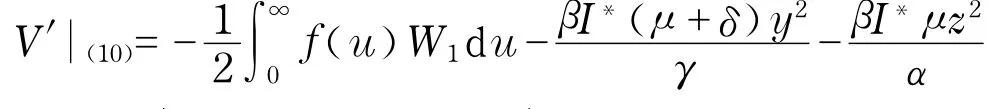
情形2 b＞0.

当b＞0时，系统（3）不存在无病平衡点.同样，由系统（3）的后两个方程可解出

将I和R代入系统（3）的第一个方程，得

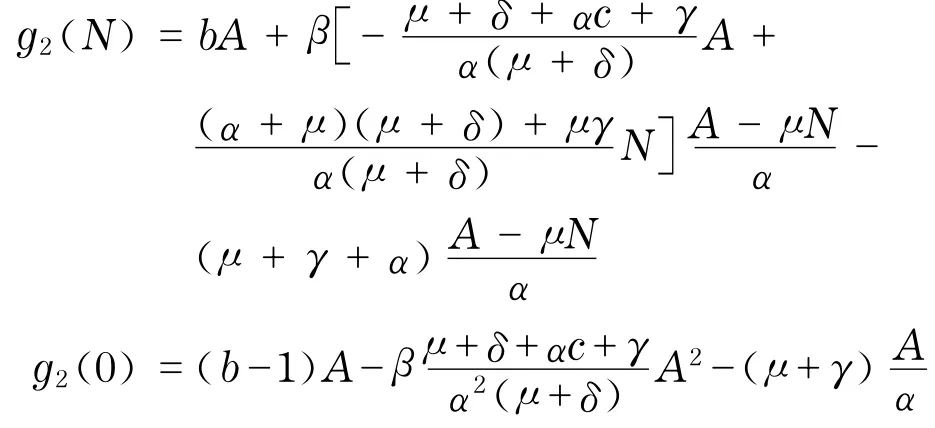
因为，b＜1，所以，g2（0）＜0.

引理1 当b＞0时，系统（3）不存在无病平衡点，只存在唯一的地方平衡点（I*，R*，N*）.

3 结束语

考虑了常数移民中具有染病者和无染病者的两种情况，利用恰当的Liapunov函数讨论了地方病平衡点全局渐近稳定的情况.

［1］ 陈军杰.一类具有常数迁入的且总人口变化的SIRI传染病模型的稳定性［J］.生物数学学报，2004，19（3）：310-313.

［2］ 李建全，张娟，马知恩.一类一般接触率和常数输入的流行病模型的全局分析［J］.应用数学与力学，2004，18（4）：359-367.

［3］ Cooke K L.Stabity analysis for a vector disease［J］. Rocky Mount J Math，1979，7（2）：253-263.

［4］ Li Jianquan，Zhang Juan，Ma Zhien.Global analysis of some epidemic models with general contact rate and constant immigration.［J］Applied Mathematics and Mechanics，2004，25（4）：396-404.

［5］ 徐金瑞，王美娟，张拥军.连续接种的具有饱和传染率和垂直传染的SIRS传染病模型［J］.上海理工大学学报，2010，32（4）：311-314.

［6］ 王贺桥，周艳丽，王美娟.具有连续预防接种的双线性传染率SIQR流行病［J］.上海理工大学学报，2007，29（2）：578-584.

［7］ 王拉娣，李建全.一类带有分布时滞的传染病模型的分析［J］.上海大学学报，2003，9（4）：354-357.

（编辑：石 瑛）

Epidemic Models of SIRS Type with Constant Immigration and Distribution Delay

ZHUChun-juan
（Colleage of Mathematics and Information Science，Shaoguan University，Shaoguan 512005，China）

An epidemic model of SIRStype with constant immigration of each class and distribution delay was dealt with by means of suitable Liapunov functions.In the absence of infectious individuals，the threshold of existence of endemic equilibrium was found.Below the threshold，the disease-free equilibrium is globally asympototically stable；above the threshold，the disease-free equilibrium is unstable and the endemic quilibrium is globally asymptotically stable.In the existence of input of infectious individuals，the models have no disease-free equilibrium and the SIRSmodel is globally stable in the corresponding region.

infectious disease model；distribution delay；equilibrium；stability

O 175.1

A

1007-6735（2013）03-0261-04

2012-04-17

朱春娟（1982-），女，讲师，研究方向：生物数学.E-mail：zhuchunjuan0079＠sina.com.cn