基于图像矩和矢量积法的六自由度机械臂视觉伺服控制

董志丹， 刘士荣， 姜宏超

（1.杭州电子科技大学自动化学院，杭州 310018；2.华东理工大学自动化研究所，上海 200237）

基于图像矩和矢量积法的六自由度机械臂视觉伺服控制

董志丹1， 刘士荣1， 姜宏超2

（1.杭州电子科技大学自动化学院，杭州 310018；2.华东理工大学自动化研究所，上海 200237）

针对眼在手上的六自由度机械臂系统，提出一种基于图像的视觉伺服控制.通过图像矩和矢量积法，建立机器人正向、逆向运动学模型，引入雅可比矩阵解决机器人逆运动学解析问题.建立了图像矩特征变化量和笛卡尔空间的关节角速度之间的映射关系即复合雅可比矩阵，由矩特征变化量得到伺服过程中六自由度机器人各关节角速度.保证在图像逼近期望图像时，机械臂末端到达期望位置，并且此时关节角速度将收敛到零.仿真结果表明，计算复合雅可比矩阵的方法可控制机械臂渐近稳定到期望位置.

图像矩；矢量积；复合雅可比矩阵；视觉伺服

Key words：image moment；vector product；composite Jacobian matrix；visual servoing

对于工作在结构化或非结构化环境中的机器人来说，视觉系统是非常重要的，将视觉和机器人控制结合起来的机器人视觉伺服最早出现于20世纪80年代，在90年代中后期发展迅速［1］.视觉伺服控制与基于传统传感器的机器人控制相比，具有更高的灵活性和精度，能够对机器人标定误差具有强的鲁棒性等优点.利用视觉位置测量，可以构成两种类型的视觉控制系统：一种利用视觉测量的位置作为给定，构成位置给定型机器人视觉控制；一种利用视觉测量的位置作为反馈，构成位置反馈型机器人视觉控制.其中位置反馈型机器人视觉控制是目前研究的主要问题，从反馈信息类型的角度，机器人视觉系统可分为基于位置的视觉伺服（PBVS）［2］、基于图像的视觉伺服（IBVS）［3］和混合视觉伺服［4］.前者的反馈偏差在3D笛卡尔空间进行计算，后者的反馈偏差在2D图像平面空间进行计算.基于图像的控制方式其期望给定值直接以图像特征信息表示，所以不需要将特征信息投影逆变换到工作空间的过程，因此基于图像的控制方式对标定误差和空间模型误差不敏感，具有更高地定位精度，为多数的视觉伺服系统所采用.

基于图像的六自由度机械臂视觉伺服控制中，最重要的是计算机械臂雅可比矩阵和图像雅可比矩阵，他们分别反映了机械臂末端运动空间与机械臂关节空间的微分映射关系和机械臂末端运动空间与任务所选择的图像特征空间的微分映射关系，即相互关系矩阵［5］.从相互关系矩阵的定义来看，它实际上是非线性的手眼映射关系在当前位置的线性近似，是一个时变模型.基于图像的视觉伺服需要根据所选用的视觉特征求取相应的图像雅可比矩阵，目前大多采用图像的简单几何特征，如点、线、圆和面积等［6-7］.图像矩是一个全局特征，虽然计算全局图像特征需要处理整幅图像数据，然而近年来在图像矩方法的研究方面有了很大的进展，计算图像矩的运算量有了显著的降低［8］.

本文提出通过图像矩特征来构造图像雅克比矩阵，克服了因纹理、照明、噪声等条件造成的匹配精度差的弱点，以机械臂为研究对象建立正向、逆向运动学模型，利用矢量积法求取机械臂雅可比矩阵.在图像雅可比矩阵和机械臂雅可比矩阵的基础上，提出了反映图像空间与机械臂关节空间微分映射关系的复合雅可比矩阵，完成基于图像的六自由度机械臂视觉伺服任务.

1 基于图像的视觉伺服系统

基于图像的视觉伺服系统如图1所示.将实时测量得到的图像信号与给定的期望图像信号直接进行在线比较，然后利用所获得的图像误差进行反馈来形成闭环控制.建立基于图像视觉伺服控制目标是将差值e（t）最小化，其定义为

式中，s是通过视觉测量的3维图像特征向量；s*是在期望位置处获得的相应图像特征向量.

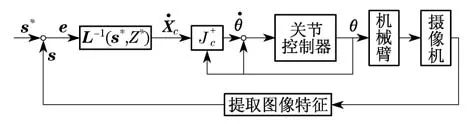
图1 基于图像的伺服系统Fig.1 Image-based visual servoing

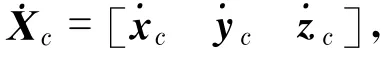
式中，Ls为图像空间和摄像机空间之间的相互关系矩阵，即图像雅可比矩阵.抓取一个静止不动的球形目标，易知˙s*=0，那么图像特征s的改变则依赖于摄像机的运动；一般情况下，如果为了保证指数收敛且˙e（t）以一定的比例减少，那么用导数等式表示闭环动态模型为

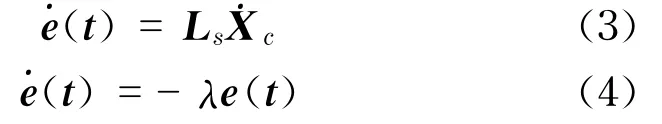
式中，λ为一个正的衰减常数.通过式（3）和式（4）可得出摄像机空间速度与差值之间的关系

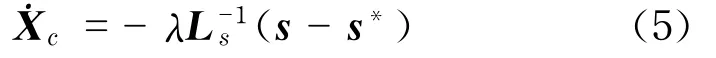
在绝大多数机器人系统中，控制量输入的都是关节运动速度˙θ，对于图1所示的系统，建立微分映射关系，即

由式（5）和式（6）可得到机器人关节运动与相应的图像特征运动之间的关系，即

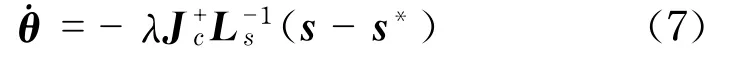
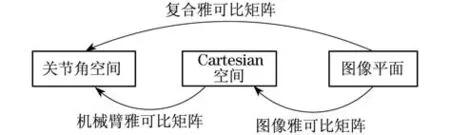
图2 复合雅可比矩阵Fig.2 Composite jacobian matrix

一般情况下，为了实现视觉伺服，必须要在线计算Ls（s，Z），即需要实时的获取深度信息Z，而目前比较常用的方法是用期望位置处的Ls（s*，Z*）作为Ls（s，Z）的估计值，这样Ls（s*，Z*）是一个常量，只需知道期望位置处目标的深度信息即可［12-13］.

2 伺服系统复合雅可比矩阵

2.1 基于图像矩的图像雅可比矩阵

一般情况下，图像矩的定义为

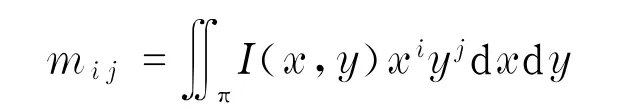
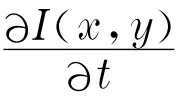
其中

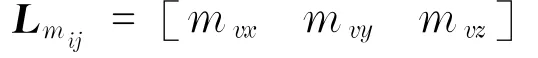
图像矩的重心和面积可以代表物体在三维Euclidean空间的位置，因此选取图像特征向量s=［xg，yg，a］T，期望位置图像特征向量s*=［x*g，y*g，a*］T，所以与所选取特征相关的图像雅可比矩阵表示为

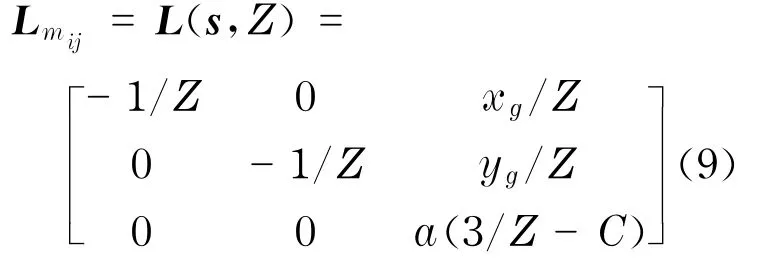
选取在期望位置处的图像雅克比矩阵L（s*，Z*）为雅可比矩阵的估计值［14］.

2.2 基于矢量积的机械手雅可比矩阵

考虑机械臂运动学方面，由于摄像机固定在机械臂的末端，故机械臂末端坐标系原点的线性速度与摄像机坐标系原点的线性速度相同.反映机械臂末端笛卡尔空间速度与关节空间速度之间关系的机器人雅可比矩阵Jc，其定义为

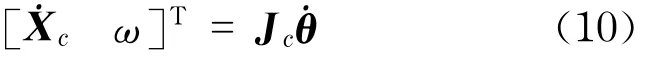
式中，ω为末端关节的角速度.通过矢量积法求取Jc，研究对象MT- ARM是具有6个旋转关节（6R）的六自由度模块化机械臂，如图3所示.根据其结构特点，使用D- H表示法确定各个旋转关节坐标系.先需定义机械臂的初始位置，然后，使用D- H方法建立基坐标系以及各个关节坐标系［15］，x0-z0表示机械臂基座的坐标系，即基坐标系，同时为关节1的坐标系，依次建立关节2～6的坐标系，x6-z6表示机械臂末端执行器的坐标系，如图4所示（见下页）.

图3 六自由度模块化机械臂Fig.3 The 6-DOF robot manipulator

建立了关节坐标系后，根据相邻关节坐标系确定关节的D- H参数表，机械臂的关节运动约束与参数如表1所示（见下页）.其中，θ表示相邻关节坐标系之间的关节角变量，d表示相邻关节之间的连杆长度，a表示相邻关节之间的连杆偏移量，α表示相邻关节坐标系之间的扭转角，各个关节角变量均以顺时针旋转方向为正.

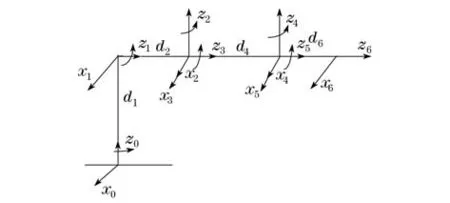
图4 六自由度模块化机械臂坐标系Fig.4 Coordinates of 6-DOF robot manipulator

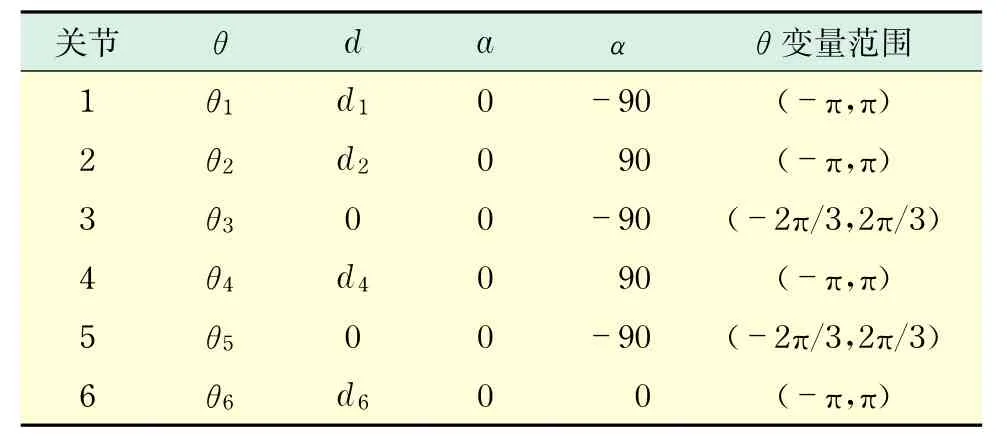
表1 MT- ARM机械臂的D- H参数表Tab.1 The D- H parameter of MT- ARM manipulator

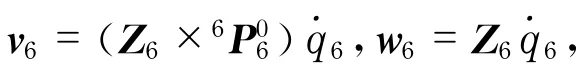
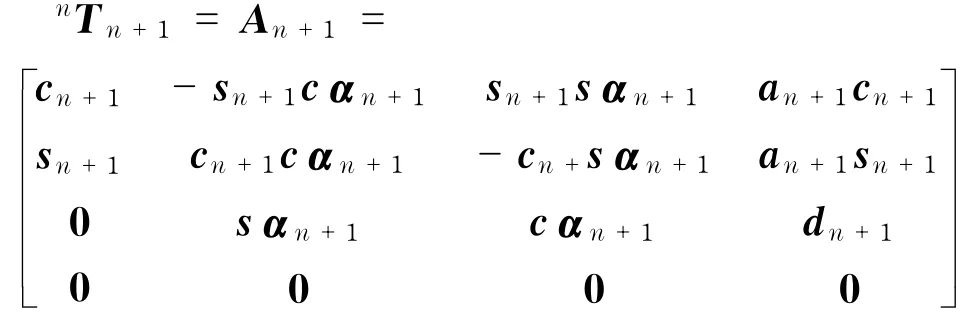
其中，nTn+1为坐标系n+1相对于坐标系n的变换，记为An+1；sαn+1，cαn+1分别为sinαn+1、cosαn+1；0Tn为关节n的坐标系相对于基座的变换矩阵，0Tn=A1…An；Zn为矩阵0Tn的第三列，旋转部分的奇次变换矩阵R是0Tn的左上角3×3的子矩阵.nT6=An…A6，末端执行器坐标原点O6到坐标系n的坐标原点On的连线矢量在坐标系n中的描述nPn6为nT6的第四列.由以上运算可得

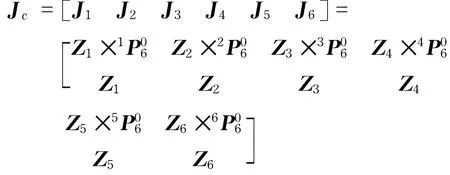
3 系统收敛性证明及离散化处理

3.1 系统收敛性证明

对图1所示的系统，建立Lyapunov函数

式中，Q为任意给定的正定矩阵.对V求导，得

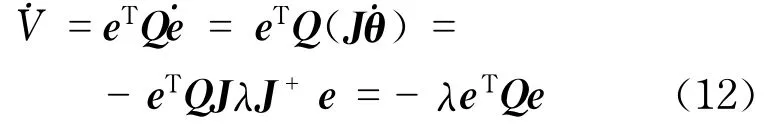
式中，J为复合雅可比矩阵，为方便起见，将矩阵Q选为单位矩阵，即Q=I，则式（12）变为

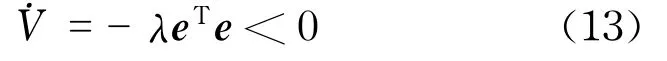
由Lyapunov稳定性判定定理，控制器在领域内渐近稳定，λ也为比例控制系数，能控制机械臂运动到期望位置.

3.2 系统离散化处理

视觉伺服是对图像特征实施提取，并根据实时获取的图像特征误差更新机械臂关节角的速度，而在伺服过程中，实际输入的是在机械臂末端上的摄像机随着机械臂运动实时拍摄的视频，下面将介绍怎么处理视频使之转化为需要的图像特征.

已知的机械臂初始位姿，得到6个关节的初始关节角θ0，得到机械手的雅克比矩阵Jc（θ0），处理视频中的第一帧图片，求出初始的关节角速度的˙θ0，计算出视频流中每一帧图像处理所需的时间Δt，由此可以求得下一帧图像处理时的关节角θ1= θ0+˙θ0Δt；根据处理得到的关节角机械臂开始运动后处理采集到的下一帧时图像，重复前面的处理计算工作，同理可以总结出t-1帧时刻˙θ（t-1），得到t帧时刻的θ（t）=θ（t-1）+˙θ（t-1）Δt，从而获得任何帧时刻的机械手雅克比矩阵，直至机械手运动至期望位置，图像特征收敛至期望图像特征，相应的关节角速度收敛至零，到达期望位置机械臂运动终止，伺服完成.实验流程如图5所示.

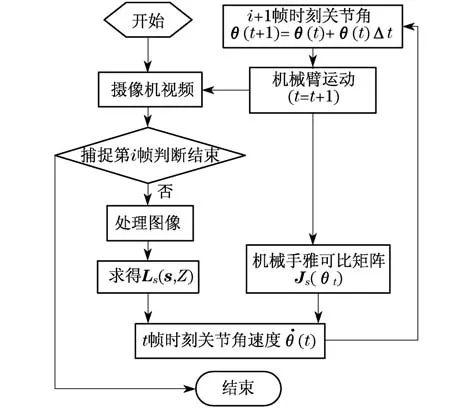
图5 实验流程图Fig.5 Flow diagram of experiment

4 仿真结果与分析

通过本文提出的视觉伺服方法，对图1描述的闭环系统进行仿真测试之后，得到如图6和图7所示的仿真结果，实验中机械臂相邻关节连杆长度d1=366.5 mm，d2=242 mm，d4=356 mm，d6= 280 mm.其中，图6表示图像特征差值随着视频帧变化的曲线，横坐标表示帧（从视频中捕捉的图片），纵坐标表示像素个数，随着图像越来越接近期望图像，矩特征变化量逼近零，机械臂末端抵达期望位置；图7表示机械臂6个关节的角速度随着视频帧变化曲线，横坐标表示帧，纵坐标表示相应关节角的角速度.随着图像趋近期望图像，相应的关节角速度也逼近零，相应的机械臂末端也抵达期望位置.

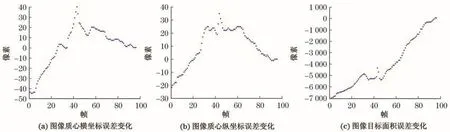
图6 图像特征差值变化Fig.6 Image characteristics difference

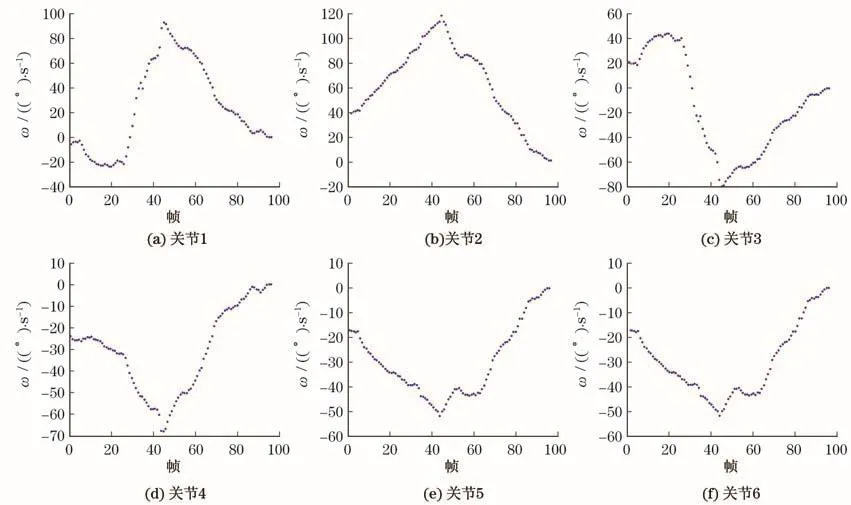
图7 六自由度机械臂6个关节角速度Fig.7 Joint angular velocity of 6-DOF robot manipulator

从仿真结果可以看出，本文所提出的计算图像雅克比矩阵的方法可控制机械臂渐近稳定的到期望位置处.

5 结束语

提出了图像不变矩和矢量积法相结合的方法，完成基于图像的六自由度机械臂视觉伺服控制，选取的图像矩特征可以很好反映目标与机械臂末端的相对位置关系.当图像矩特征与期望位置处图像矩特征匹配时，关节角速度收敛至零，并且机械臂末端抵达期望位置，运动停止.实验结果表明，在图像特征逐渐靠近期望位置图像特征的过程中该方法的有效性.未来主要工作将研究机械臂对运动目标的伺服控制.

［1］ 徐德，谭民，李原.机器人视觉测量与控制［M］.北京：国防工业出版社，2011：200-255.

［2］ Wilson W J，Hulls C C，Bell G S.Relative end-effector control using Cartesian position-based visual servoing［J］.IEEE Trans on Robotics and Automation，1996，12（5）：684-696.

［3］ Deguchi K.Optimal motion control for image-based visual servoing by decoupling translation and rotation，in proceedings intelligent robots and systems［C］∥IEEE／RSJ International Conference.Victoria：1998，705-711.

［4］ Malis E，Chaumette F.2 1／2 d visual servoing with respect to unknown objects through a new estimation scheme of camera displacement［J］.Int Journal of Computer Vision，2000，37（1）：79-97.

［5］ Chaumette F，Hutchinson S.Visual servo control，part i：Basic approaches［J］.IEEE Robotics and Automation Magazine，2006，13（4）：82-90.

［6］ Feddema J T，Lee C S G，Mitchell O R.Weighted selection of image features for resolved rate visual feedback control［J］.IEEE Trans on Robotics and Automation，1991，7（1）：31-47.

［7］ Papanikolopoulos N P，Khosla P K.Feature based robotic visual tracking of 3-D translational motion［J］.Proc of the 30th on Decision and Control，1991（17）：1877-1882.

［8］ Martinez J，Thomas F.A reformulation of gray-level image geometric moment computation for real-time applications［J］.Proc of IEEE Int，Conf on Robotics and Automation，1996（3）：2315-2320.

［9］ Chaumette F，Hutchinson S.Visual servo control，part ii：advanced approaches［J］.IEEE Robotics and Automation Magazine，2007，14（1）：109-118.

［10］ Espiau B，Chaumette F，Rives P.A new approach to visual servoing in robotics［J］.IEEE Trans on Robotics and Automation，1992，8（3）：313-326.

［11］ Siradjuddin I，Behera L，McGinnity T M，et al.Image based visual servoing of a 7 DOF robot manipulator using a distributed fuzzy proportional controller［C］∥IEEE International Conference on Fuzzy Systems（FUZZ），Barcelona：2010，1-8.

［12］ Chaumette F.Image moments：a general and useful set of features for visual servoing［J］.IEEE Trans On Robotics，2004，20（4）：713-723.

［13］ Corke P，Hutchinson S.A new partitioned approach to image based visual servo control［J］.IEEE Trans Robot Automat，2001（17）：507-515.

［14］ Chaumette F，Hutchinson S.Visual servo control part I：basic approaches［J］.IEEE Robotics and Automation Magazine，2006，（6）：82-90.

［15］ 谭民，徐德，侯增广，等.先进机器人控制［M］.北京：高等教育出版社，2007：20-81.

［16］ 蒋刚，龚迪琛，蔡勇，等.工业机器人［M］.成都：西南交通大学出版社，2010：26-46.

（编辑：金 虹）

Visual Servoing Control of a 6-DOF Robot Manipulator Based on Image Moments and Vector Product

DONGZhi-dan1， LIUShi-rong1， JIANGHong-chao2
（1.School of Automation，Hangzhou Dianzi University，Hangzhou 310018，China；2.Research Institute of Automation，East China University of Science and Technology，Shanghai 200237，China）

A visual servoing method based on image for a 6 DOF robot manipulator was proposed. On the basis of image moments and vector product，Jacobian matrix was introduced to resolve problems in robotic inverse kinematics by building robotic forward kinematics model and inverse kinematics model.Furthermore the composite Jacobian matrix was established，which stands for the mapping relationship between the image characteristic variation and joint angular velocity in Descartes space.The joint angular velocity of the manipulator in visual servoing was obtained from the variation of moments characteristic，ensuring that when the image approximates to the expected one，the manipulator can reach the desired place and the joint angular velocity converges to zero at the same time.The simulation results show that the method proposed to calculate the composite Jacobian matrix can control the manipulator to reach the expected position.

TP 24

A

1007-6735（2013）03-0221-06

2013-05-10

国家自然科学基金资助项目（61175093）

董志丹（1986-），女，硕士研究生.研究方向：先进机器人与智能系统.E-mail：dongzhi.dan＠163.com

刘士荣（1952-），男，教授.研究方向：新能源电力与智能微电网技术、智能机器人与智能控制.E-mail：liushirong＠hdu.edu.cn