结渣初始层沉积物热力学性质的第一性原理计算
李明强, 杜梅芳, 乌晓江, 张忠孝
(1.上海理工大学理学院,上海 200093;2.上海锅炉厂有限公司,上海 200245;3.上海交通大学机械与动力工程学院,上海 200240;)
结渣初始层沉积物热力学性质的第一性原理计算
李明强1, 杜梅芳1, 乌晓江2, 张忠孝3
(1.上海理工大学理学院,上海 200093;2.上海锅炉厂有限公司,上海 200245;3.上海交通大学机械与动力工程学院,上海 200240;)
为了解煤灰在洁净的水冷壁附近选择性沉积的微观机理,以及进一步解决复杂的结渣问题,采用第一性原理(first-principles)的超软赝势平面波方法,对Al2O3、SiO2、和Fe2O3的电子结构、热力学性质进行了计算;结构优化,使这3种矿物质达到最稳定的结构,并计算出这3种矿物质的电子结构、晶胞参数;根据声子谱态密度方法,得出这3种矿物质的温熵积、焓、吉布斯自由能及比定压热容;由相关的数据拟合图像.
热力学性质;电子结构;声子谱;煤灰;第一性原理
由于煤灰结渣过程涉及多个学科,包括材料科学、煤及灰渣化学、反应动力学、锅炉原理、多相流体力学、燃烧理论与技术、传热传质学等,所以其过程非常复杂.目前在工程领域,预测结渣倾向的方法是基于经验指标,因此在效果上不很理想.据统计,我国有一半以上的电站锅炉有积灰结渣的问题[1].对于结渣的机理,已经有大量的文献从宏观方面进行了讨论[2-4],从宏观的研究结果可以看出,初始沉积层是结渣最终生成的基础,它一旦形成,就为煤灰的进一步沉积创造了有利条件,此后沉积层的厚度将随时间按指数的关系增长.炉内灰粒向水冷壁扩散的机理有3种,其中的扩散和热迁移在初始沉积层的形成过程中起着主要作用[5],只有当灰粒的尺寸小于5 um时才能受这两个作用的影响,石英SiO2、矾土Al2O3和赤铁矿Fe2O3[6]是这些灰粒的主要成分,值得注意的是,在煤灰中含量较少的Fe2O3却在初始沉积层中大量的沉积.对于这种选择性沉积的解释还少有报道,所以,对这3种矿物作更深入的微观分析对比是非常必要的.
第一性原理即从头算方法(first-principles or ab initio),其仅用最基本的常数,没有任何其它经验数据的依赖,求出薛定谔方程,就可以去预测特定材料体系的性质和状态.因此,它是基于量子力学和量子密度泛函理论而发展起来的一种理论性很强的方法.随着计算机技术飞速发展,近年来,在固体力学的性质和电子结构等方面,用第一性原理的研究方法取得了很大的成效[7-8].在煤灰中无机矿物质的结构模型的研究方面,也对矿物质宏观的特性作了很好的解释,并且预测了一些现象[9].本文通过对SiO2、Al2O3和Fe2O3的电子结构、热力学性质的计算,给出了煤灰结渣初始层主要沉积矿物质的热力学性质随温度的变化规律,以此为进一步研究提供理论依据.
1 实验和计算方法
1.1 实 验
实验所用样品取自一台来自扬子石化公司热电厂的220 t/h四角切圆的燃烧锅炉,该炉用平朔烟煤做燃料,它的煤质分析数据是挥发分Vad=25.23%,水分Mad=3.23%,发热量Q net,ad=20.74 MJ/kg,灰分Aad=32.46%,硫含量St,d=0.97%.4种样品的质量分数和X—射线衍射的分析结果见表1.
表中数据表明,实验室煤灰与炉内飞灰的成分相差不大,这是由于煤中无机组分在炉内转变成煤灰后绝大多数以飞灰的形式排出炉外;与此相比,结渣沉积物中则出现了明显的铁富集现象,无论内层还是外层沉积物都是如此,且以内层沉积物中更为明显.

表1 各试样的灰成分分析和X-射线衍射分析结果[6]Tab.1 Results of sample compositions analysis and X-ray diffraction analysis
Al2O3、SiO2和Fe2O3都属于三方晶系,其空间群分别为R- 3cH、P3221、R- 3cH,晶面角都为α= β=90°,γ=120°,晶格常数分别为:Al2O3,a=b= 0.475 400 nm,c=1.299 001 nm;SiO2,a=b= 0.491 370 nm,c=0.540 512 nm;Fe2O3,a=b= 0.503 800 nm,c=1.377 201 nm.计算模型体系的晶胞三维结构如图1所示.
1.3 计算方法和理论
在密度泛函的总能计算中,依据Perdew等提出的广义梯度近似[10],并且利用Materials Studio软件包中的CASTEP[11]模块,基于第一性原理的超软赝势[12]平面波方法,用赝势替代离子势,用平面波基组将电子波函数展开,采用BFGS算法进行结构优化[13],对Al2O3、SiO2和Fe2O3的结构进行模拟计算,该理论的关键是求解Kohn-Sham方程

1.2 模型构建
其中
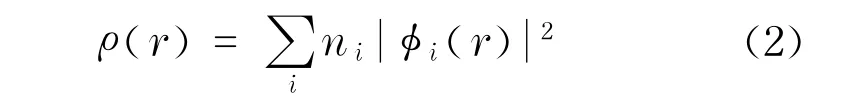
式中,hks为本征值;Zq为原子核电荷数;r,r′为电子矢量位置;Rq为原子核的矢量位置;φi(r)为波函数;右端中括号中第一项为动能;第二项为分子中各个原子核和电子的库仑相互作用项;第三项是电子间的库仑相互作用项;Vxc为交换相关项;ρ(r)为电荷密度;ni为占有数;φi(r)为原子簇与分子单电子的波函数.在此基础上,用平面波的赝势公式对这3种矿物质的结构进行几何优化,得出相应矿物质的晶胞结构参数.在几何优化计算的过程中,为了保证计算的精度,总能量精度设置一个原子的能量为1.0×10-5eV,能量截断值设置为350.0 eV.每个原子所受的晶体内的作用力小于0.3 eV/nm,每个结构单元的应力小于0.005 GPa,从而使其在几何优化下尽量地接近真实结构.在计算时,选取这些矿物质的晶体原胞为周期性边界条件,采用Monkhost-Pack方法,布里渊区积分的K点网格尺寸依次为3 ×3×2,3×3×4,3×3×2.

图1 Al2O3、SiO2和Fe2O3三维结构Fig.1 3D-structures of bauxite,quartz and hematite
求得基态的电荷密度后,经过自洽迭代的方法求得声子频率分布.通过声子的态密度,就能得知这3种矿物质的热力学性质.
晶格振动对自由能的贡献
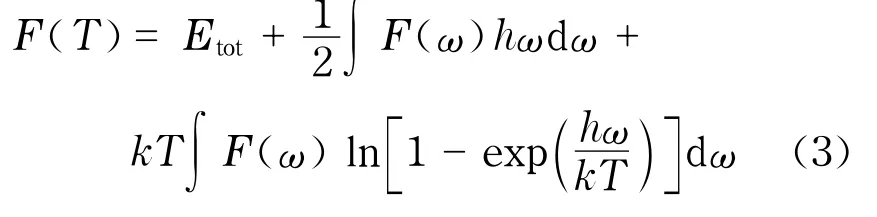
式中,F为自由能;Etot为平衡晶格能量;h为普朗克常数;ω为格波频率;k为波尔兹曼常数;T为温度.
熵S随温度变化

热容cv随温度变化

式中,cp为比定压热容;α线性热膨胀系数;B为体弹模量.

讨论是在定压情况下压强和体积变化的值很小,可以忽略,所以用自由能代替吉布斯自由能.
2 结果与讨论
2.1 优化结构与分析
经几何优化与计算后,得到Al2O3、SiO2和Fe2O3最稳定的结构,对应的晶胞参数、晶胞体积V0如表2所示(见下页).图2为经过优化与计算后而得到的3种矿物质电子结构示意图.

图2 Al2O3、SiO2和Fe2O3三维电子结构Fig.2 Electronic structures of bauxite,quartz and hematite
其中Al2O3、SiO2和Fe2O3中各原子参与计算的价层电子组态分别为Al 3s23p1,Si 3s23p2,Fe 3d64s2,O 2s22p4.由于考虑到晶胞顶点、晶向、晶面的原子对晶体单元的贡献依次为1/8,1/4和1/2,由此可得各矿物质晶胞内有效原子个数分别为Al2O3中 Al原子、O原子依次为12个和18个;SiO2中的Si原子、O原子依次为3个和6个;Fe2O3中的Fe原子、O原子依次为12个和18个.与计算模拟的结果完全一致.表2给出了经过优化后得到3种矿物质的各项晶胞参数.

表2 优化后的晶胞参数Tab.2 Optimized crystal cell parameters
由上表可知,在这样的参数设置下计算得出的结果与实验值很相符,其它性质的计算也与实际相符.
2.2 热力学性质计算
经过几何优化,使Al2O3、SiO2和Fe2O33种矿物质达到稳定结构,然后根据第一性原理求得基态电荷密度,经过自洽迭代求得声子频率分布,再由声子谱态密度,相应求得这3种矿物质的热力学性质.对于热力学性质的计算,是在1个大气压下,热力学温度是从5~1 000 K,间隔为20 K,这样,每种矿物质的各热力学量均得到50组数据.根据以上的计算结果,作出这3种矿物质的温熵积TS、比定压热容cp、焓H及吉布斯自由能G随温度变化的曲线,见图3所示.

图3 各参数随温度变化曲线Fig.3 Parameters change with temperature curve
由图3可看出,3种矿物质的TS、cp、H均随温度升高而增大,只有G随温度的升高而减小,符合基本的热力学规律.图3(a)显示,在0~100 K的范围内,3种矿物质的温熵积基本不变,且近似相等.之后开始增加,在500 K之后几乎都成线性增长,且Fe2O3的增率始终低于其它两种矿物质.图3(b)显示,在0~200 K的范围内,3种矿物质的比定压热容几乎成线性增长,且增率几乎相同.在200~600 K的范围内,SiO2和Fe2O3的比定压热容增率一直是减小的趋势,而Al2O3的比定压热容增长率确是先增大后减小.600 K之后,3种矿物质的比定压热容都趋于一个定值,其中Fe2O3的比定压热容最小.图3(c)显示,在0~100 K的范围内,3种矿物质的温焓基本不变,且近似相等.200~400 K它们的焓还是增加,且Al2O3增率大于其它两种,400 K之后,3者的焓几乎都成线性增长,且SiO2和Fe2O3的焓值相近.图3(d)显示,3种矿物质的吉布斯自由能随温度升高而减小.在0~400 K的范围内,3种矿物质的吉布斯自由能变化趋势相近,之后,SiO2和Fe2O3的吉布斯自由能降低的趋势高于Al2O3.
3 结 论
从微观的角度出发,利用第一性原理的方法对初始层的物质进行模拟计算,先求出基态的电荷密度,进而,通过自洽迭代得到声子频率的分布,然后利用声子谱的态密度,相应求得Al2O3、SiO2和Fe2O3的热力学量在不同温度下的数值.结合相应的数据作出这3种矿物质的各热力学量随温度的变化规律曲线并作比较.通过这样的方法,在不需要经验或半经验的条件下,研究了初始层主要矿物质的热力学性质和微观结构,为进一步研究除渣的问题提供一定的理论依据.
[1] 徐志明,杨善让,王建国,等.管式换热器积灰特性的实验研究[J].工程热物理学报,2002,23(2):203 -205.
[2] Bryers R W.The physical and chemical characteristics of Pyrite and their influences on fireside problems in steam generators[J].Journal of Engineering for Power-Transactions of the ASME,1976,98(4):517-527.
[3] Srinivasachar S,Boni A A,Kinetic A.Model for pyrite transformations in a combustion environment[J]. Fuel,1989,68(7):829-836.
[4] Erickson T A,Allan S E,Mccollor D P.Modeling of fouling and slagging in coal-fired utility boilers[J].Fuel Processing Technology,1995,44(1/3):155-171.
[5] Wang H F,Habr J N.Modeling of ash deposition in lgare-scale combustion facilities burning pulverized coal[J].Progress in Energy and Combustion Sciences,1997,23(3):267-282.
[6] 盛昌栋,华永明,周强泰,等.煤中FeS2和含铁粘土矿物在锅炉结渣过程中的作用[J].燃烧科学与技术,1999,5(3):246-250.
[7] 杜晔平,陈敬超,冯晶.不同SnO2晶体结构的力学性能及电子结构[J].物理化学学报,2009,25(2):278 -284.
[8] 管嵘清,杜梅芳,李洁,等.煤灰中霞石与钠长石的光学性质对熔融特性影响[J].上海理工大学学报,2010,32(6):597-601.
[9] 王宝俊,张玉贵,谢克昌.量子化学计算在煤的结构与反应性研究中的应用[J].化工学报,2003,54(4):477 -488.
[10] Perdew J P,Chevary J A,Vosko S H,et al.Atoms,molecules,solids,and surfaces:applications of the generalized gradient approximation for exchange and correlation[J].Phys Rev B,1992,46(11):6671 -6687.
[11] Segall M D,Lindan P J D,Probert M J,et al.Firstprinciples simulation:ideas,illustrations and the CASTEP code[J].J Phys:Condens Matter,2002,14(11):2717-2744.
[12] Vanderbilt D.Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J].Phys Rev B,1990,41(11):7892-7895.
[13] Fischer T H,Almlof J A.General methods for geometry and wave function optimization[J].J Phys Chem,1992,96(24):9768-9774.
[14] Ishizawa N,Miyata T,Minato I,et al.A structural investigation of ALPHA-Al2O3at 2170 K[J].Acta Crystallographica B,1980,36(2):228-230.
[15] Smith G S.Alexander L E.Refinement of the atomic parameters of ALPHA-QUARTZ[J].Acta Crystallographica,1963,16(3):462-471.
[16] Blake R L,Hessevick R E,Tibor Z,et al.FINGER,Refinement of the hematite structure[J].American Mineralogist,1966,51(1):123-129.
(编辑:金 虹)
First-principles Calculation of Thermodynamic Properties of Initial Layer Sediments
LIMing-qiang1, DUMei-fang1, WUXiao-jiang2, ZHANGZhong-xiao3
(1.College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China;2.Shanghai Boiler Works Co Ltd,Shanghai 200245,China;3.School of Mechanical Engineering,Shanghai Jiaotong University,Shanghai 200240,China)
In order to know the microscopic mechanism of selective deposition of coal ash in the area nearby clean water wall and to provide some theoreticsl basis to solve the problem of complex slagging,the ultrasoft pseudo-potential plane-wave method was introduced based on the firstprinciple to calculate the electric structure and thermodynamic properties of Al2O3,SiO2and Fe2O3. The most stable structure was achieved and the electric structure and cell parameters of the three materials were calculated.Then the thermodynamic properties were derived and the temperature entropy product T*S,heat capacity cp,enthalpy H and Gibbs free energy G of the three minerals were obtained in the light of the metod of phonon spectra state density.Corresponding curves were fitted with the data acguired.
thermodynamic property;electronic structure;phonon spectra;coal ash;first-principles
O 641;O 642
A
1007-6735(2013)03-0265-05
2012-05-29
国家自然科学基金资助项目(51276212);上海市青年科技启明星计划资助项目(11QB1402100)
李明强(1983-),男,硕士研究生.研究方向:煤灰量化研究.E-mail:limingqiang911@163.com
张忠孝(1959-),男,教授.研究方向:分级燃烧、气流床气化及节能减排技术.E-mail:zhzhx222@163.com

