惯性质量对馈能悬架阻尼特性和幅频特性的影响
刘松山,王庆年,王伟华,林 鑫
(吉林大学 汽车仿真与控制国家重点实验室,长春130022)
馈能悬架指能够回收悬架振动能量并衰减车轮与车身间振动的新型减振器。本文研究的馈能悬架由滚珠丝杠式馈能减振器和与之并联的弹簧组成,其中馈能减振器由滚珠丝杠、电机和电池组成,分别作为运动转化、回收能量以及电能储存的部件。相比于传统的减振器,馈能减振器包含丝杠和电机等旋转部件,这使得其输出力不仅仅包含与悬架的相对运动速度有关的阻尼力,还包含与悬架的相对运动加速度有关的惯性力。惯性力的引入将使传统减振器的阻尼特性和传统悬架的幅频特性发生改变,从而对悬架的性能产生影响。过去20年间,学者们对悬架的振动能量回收潜力、馈能结构和控制策略等方面进行了大量研究[1-3],也有一些文献提到了惯性质量的存在[4-6],但均未对其进行深入研究。
本文首先建立了馈能减振器模型,分析了惯性力对阻尼特性的影响。然后利用结构振动分析方法,求得惯性力对于馈能悬架固有频率及传递特性的影响,进而求得惯性质量对馈能悬架性能指标幅频特性的影响。
1 馈能减振器的阻尼特性分析
馈能减振器通过滚珠丝杠将悬架的直线运动转化为旋转运动,随着悬架的上下跳动带动电机转动,同时电机产生与运动方向相反的扭矩,电机处于发电状态,从而能够回收能量和衰减振动。通过对馈能电机的主动控制可以产生所需的制动扭矩,丝杠将电机的扭矩转化为悬架的直线阻尼力Fd此外,馈能减振器中旋转部件在悬架加减速运动过程中,会产生与馈能减振器系统惯量成正比的惯性力Fi,因此馈能减振器的输出力Frg将是阻尼力和惯性力的合力,如式(1)所示:

1.1 馈能减振器模型
馈能减振器的Matlab/Simulink模型包括永磁同步电机(PMSM)及其矢量控制模型[7](VECT)、电池模型、馈能减振器控制器模型4个部分。整个模型的输入为悬架运动的速度和加速度,输出为馈能减振器的阻尼力Frg。馈能减振器的作用力包含馈能阻尼Fd和惯性力Fi两部分,如图1所示。
馈能减振器的控制系统根据悬架的运动速度v和加速度a计算出相应的馈能电机转速ω,参考扭矩T*和惯性力Fi,ω作为馈能电机的输入,T*作为馈能电机控制器的输入。馈能电机控制器通过矢量控制使馈能电机的输出扭矩跟随参考扭矩。馈能电机输出扭矩Tm通过丝杠转化为馈能阻尼力Fd,并和惯性力Fi之和作为馈能减振器的输出。馈能电机和电池模型分别为Simulink自带的永磁同步电机模型(PMSM)和Lithium-Ion模型。
1.1.1 馈能阻尼力的确定

图1 馈能减振器模型Fig.1 Regenerative damper model
匹配的馈能减振器的阻尼系数Cs=1500N·s·m-1,所匹配的馈能电机的额定功率Prated=500W,过载系数为2,最高转速为6000r/min,基速比为3,二者的阻尼区间对比如图2所示(参考文献[8滚珠丝杠式馈能型减振器的结构设计及参数匹配的方法)。馈能电机的最大速度为1.6m/s,额定工作范围内可满足的减振器速度-力特性的最大速度点为0.59m/s,在过载区间内可满足的最大速度点为0.83m/s,如图2所示。

图2 馈能电机阻尼区间与传统阻尼区间对比Fig.2 Comparison of regenerative motor and conventional damping region
根据悬架的运动速度v计算所需阻尼力,再与此速度对应的馈能电机的最大阻尼力进行比较,两者取较小值得出阻尼力的参考值,再转化为参考扭矩T*发送给电机控制器,如图3所示。

图3 馈能悬架阻尼力计算Fig.3 Calculation of regenerative damping force
由电机特性可知,当旋转速度大于额定转速时,电机可以提供的制动扭矩会随着速度的增大而减小。因此,当减振器的速度大于馈能电机满足速度-力特性的最大速度点(0.83m/s)后,会进入阻尼不足区间,其可提供的阻尼会随着速度的增大而减少,这种现象也会对馈能减振器的阻尼特性造成影响,但此匹配结果基本可以满足E级路面行驶要求,即不会出现阻尼不足的情况,因此本文暂不讨论阻尼不足对阻尼特性的影响,馈能阻尼力与所匹配的传统阻尼力相同,可由下式表示:

1.1.2 惯性力的计算
馈能减振器旋转部件包括电机转子和丝杠,这部分旋转质量引入的惯性力可由下式表示[8]:

式中:Jm和Js分别为馈能电机和丝杠的转动惯量;z··为悬架的相对运动加速度;mr为馈能减振器的等效惯性质量。
1.2 阻尼特性分析
馈能减振器输出力中阻尼力仅与激励速度有关系,而惯性力还与激励频率有关,因此令正弦激励的最高速度均为0.524m/s,分别取低、中、高3个频率去考虑馈能减振器的阻尼特性。图4和图5分别为激励频率为2、5、10Hz时,馈能阻尼器的速度-力特性和示功特性。

图4 减振器阻尼特性曲线Fig.4 Characteristic diagram of damper

图5 减振器示功图Fig.5 Indicator diagram of damper
图5 中虚线和实线分别表示馈能减振器和与之对应的传统减振器的示功特性,从图中可以看出:惯性力的引入使传统的阻尼特性曲线和示功特性曲线产生滞环和相位差,而且随着激励频率的增大,滞环和相位差会增加。经分析可知,滞环现象是由于馈能减振器受正弦激励时,速度项的阻尼力和加速度项的惯性力之间相位差为90°。在半个周期内,速度从0到最大值vmax与从最大值vmax再到0以及速度从0到最小值vmin与从最小值vmin到0时,惯性力对于阻尼力的影响正好相反,一个是增强一个是减弱,因此表现在阻尼特性时,就会出现滞环。另外滞环现象与惯性质量的大小有直接关系。
2 馈能悬架的幅频特性分析
惯性力的引用使得悬架的运动方程发生改变,这种改变将会对悬架的传递特性产生影响。图6为二自由度的馈能悬架示意图,馈能电机置于车身上方,可以有效地减小馈能减振器的安装空间。建立其运动方程如式(4)所示:

式中:z=zw-zb;mb为簧载质量;mw为非簧载质量;mr为等效惯性质量;ks为弹簧刚度;kt为轮胎刚度;Cr为馈能减振器等效阻尼系数。

图6 馈能悬架1/4车辆模型Fig.6 1/4Vehicle model with regenerative suspension
2.1 馈能悬架的固有频率
惯性质量的引入会改变悬架系统的固有频率,若求该振动系统的固有振型,首先将式(4)变成无阻尼自由振动方程:

由于馈能悬架的质量阵和刚度阵均不是对角阵,所以无法直接求得系统的固有频率。由结构振动分析[9]可知,馈能悬架的簧载质量和非簧载质量无阻尼自由振动为同步运动,设两个质量zw、zb以相同的圆频率ω和相角φ作简谐运动,振幅分别为z10、z20,则其解为

将同步解带入无阻尼运动方程组(5得:

该方程组有非零解的条件是系数行列式等于零,即:

进而得到馈能悬架系统的两个固有频率:


2.2 馈能悬架的传递特性
传递特性可描述馈能悬架簧载质量和非簧载质量对外部激励的响应情况。当路面激励q为谐波激励时,q=Qeiωt,其中Q为谐波激励的幅值。设系 统 的 稳 态 响 应 分 别 为zw=Zweiωt、zb=Zbeiωt,代入式(4),经整理可得:

式中:

根据克莱姆(Cramer)法则[10],可求得车轮和车身的频率响应。对于馈能悬架,当匹配的阻尼系数为Cr时,悬架的阻尼比可表示为激励频率ω与无惯性质量的车身固有频率ω0的比值为λ=ω/ω0,经过整理可得馈能悬架系统的传递特性:

通过与汽车理论[11]中传统悬架的传递特性对比,可发现当令β=0时,二者完全相同。
本文研究的馈能减振器系统惯量主要取决于馈能电机的惯量,而馈能电机的惯量主要与所匹配的电机的功率有关(同功率的电机用途不同其惯量也有较大的差别),功率越大惯量越大。为了研究惯量比β对悬架的传递特性的影响,取参数μ=0.1,ζ=0.25,分别取β=0,0.25,0.5,0.75,1,谐波激励的频率为0~30Hz,可得到不同β的馈能悬架的传递特性,如图7所示。
图7(a)为车轮对路面激励的幅频特性|zw/q|。相比于传统悬架,馈能悬架的车轮共振频率随着β的增大而减小(共振频率可以通过式(10)求得),而且共振峰值随着β的增大而增大,这导致车轮中频振动特性变坏,而高频特性有一定的改善。
图7(b)为车身对车轮激励的幅频特性。当激励频率增大时,传统悬架的该幅频特性收敛于零,而馈能悬架则不收敛于零,这点对高频振动是不利的。从式(11)可看出,激励频率趋于无穷大,β=0(即为传统悬架)时,|zw/zb|→0;而当β≠0(即为馈能悬架)时,|zw/zb|→μβ/(1+μβ),随着β的增加,幅频特性将收敛于更大值。
图7(c)为车身相对路面激励的幅频特性|zw/q|,它可由幅频特性|zb/q|和|zw/zb|相乘得到。从图中可看出:相对传统悬架,馈能悬架的车身共振频率随着β的增大而减小,而共振峰值有一定程度的减小,但影响不大;而车轮共振峰处,共振峰值随着β的增大而增大;而在高频时,由于|zw/zb|不收敛于零,导致车身高频传递特性变差。
2.3 车身加速度、悬架动挠度和车轮相对动载的幅频特性

图7 馈能悬架的传递特性Fig.7 Transfer characteristics of regenerative suspension
由前面的分析可知,惯性质量的引入使得阻尼特性、悬架的固有频率及传递特性发生改变。但最终关注的是β对悬架系统性能指标(车身加速度(z··w)、悬架动挠度(fd)和车轮相对动载荷(Fd/G))的影响。分别取β=0,0.25,0.5,0.75,1,分析其对3个性能指标的影响。
2.3.1 车身加速度幅频特性
车身加速度是车辆平顺性的重要指标。根据式(12)中|zw/q|幅频特性,可求得车身加速度对于路面激励q·的幅频特性:


图 8的幅频特性曲线Fig.8 Amplitude-frequency curve of
前节仿真所选用的馈能减振器等效惯性质量mr=12kg,假设车轮的质量mw=40kg,可得β=0.3。从图8中可看出:惯性质量对馈能悬架的共振峰值和高频特性影响并不严重,但仿真采用的馈能电机为小功率和小惯量电机,惯性质量较小,实际馈能电机惯量大于这个值。
2.3.2 悬架动挠度的幅频特性
悬架动挠度(fd)代表悬架系统在振动中压缩的程度,其随激励频率的变化会影响悬架系统在不同频率路面激励的情况下,悬架系统撞击限位块的概率,从而间接影响车辆平顺性,根据式(12)中|zw/q|和|zb/q|的幅频特性,可求得悬架动挠度fd对路面激励q·的幅频特性:

2.3.3 车轮相对动载的幅频特性
车轮的相对动载是车辆行驶安全性的重要指标。根据式(12)中幅频特性|zw/q|,可求得车轮相对动载对路面激励q·的幅频特性

图9 的幅频特性曲线Fig.9 Amplitude-frequency curve of
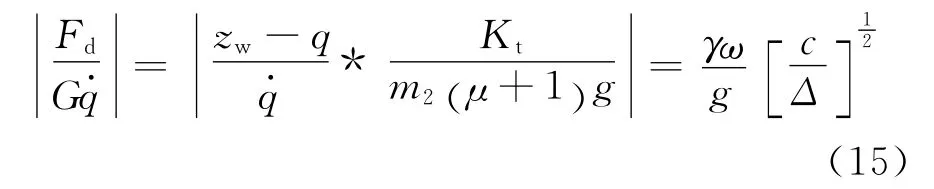

图10 )的幅频特性曲线Fig.10 Amplitude-frequency curve of
3 结束语
针对以往关于惯性质量对馈能悬架的影响理论分析不足,本文通过仿真和结构振型的方法对二自由度的馈能悬架进行了分析。结果表明:惯性质量会使馈能减振器的线性阻尼特性曲线出现滞环和相位差,且二者随激励的频率和惯性质量的增加而增加。馈能悬架的车身和车轮固有频率会降低,使得低频段和车身共振段性能有所改善,而恶化了车轮共振段的性能;更高激励频率时主要是对平顺性不利,对安全性则影响不大。因此必须对馈能系统的惯性质量进行限制或者通过对馈能电机的主动控制来减小惯性力对车轮共振段和高频的不利影响。
[1]Suda Y,Nakadai S,Nakano K.Hybrid suspension system with skyhook control and energy regeneration[J].Vehicle System Dynamics,1998,29(Sup.1):619-634.
[2]于长淼,王伟华,王庆年.混合动力车辆馈能式悬架的节能潜力[J].吉林大学学报:工学版,2009,39(4):841-845.Yu Chang-miao,Wang Wei-hua,Wang Qing-nian.Analysis of the potential benefits of energy regenerative suspension system on hybrid vehicle[J].Journal of Jinlin University(Engineering and Technology E-dition),2009,39(4):841-845.
[3]Sagiv Bar David,Ben Zion Bobrovsky.Actively controlled vehicle suspension with energy regeneration capacities[J].Vehicle System Dynamics,2011,49(6):833-854.
[4]Yasuhiro K,Yoshihiro S,Hirofumi I.Modeling of electromagnetic damper for automobile suspension J.Journal of System Design and Dynamics2007 1(3):524-535.
[5]Jonasson M,Roos F.Design and evaluation of an active electromechanical wheel suspension system[J].Mechatronics,2008,18(4):218-230.
[6]于长淼,王伟华,Subhash R,et al.双超越离合器式电磁馈能阻尼器原型机试验测试与分析[J].吉林大学学报:工学版,2012,42(2):292-297.Yu Chang-miao,Wang Wei-hua,Subhash R,et al.Experiments and analysis of the dual-overrunning clutches electro-mechanical regenerative damper prototype[J].Journal of Jilin University(Engineering and Technology Edition),2012,42(2):292-297.
[7]王成元,夏加宽,孙宜标.现代电机控制技术[M].北京:机械工业出版社,2008.
[8]Liu Song-shan,Wei Hao,Wang Wei-hua.Investigation on some key issues of regenerative damper with rotary motor for automobile suspension[C]∥2011International Conference on Electronic and Mechanical Engineering and Information Technology(EMEIT),Harbin,China,2011:1435-1439.
[9]陈宇东.结构振动分析[M].长春:吉林大学出版社,2008.
[10]Dave Corolla,喻凡.车辆动力学及其控制[M].北京:人民交通出版社,2003.
[11]余志生.汽车理论[M].北京:机械工业出版社,2006.

