高频链矩阵式正弦波变换器控制策略的改进

吴胜华 钟炎平 赖向东 权建洲

（空军雷达学院 武汉 430019）

1 引言

1970年，MeMurray 提出的高频链相控DC-AC变换器，取消了传统的工频变压器，既提高了装置的功率密度，减轻了重量，而且功率可以双向流动。因此，该类变换器可广泛应用于要求装置“小型轻量”且需电气隔离的场合，如车载或某些移动设备中特殊电源、小功率UPS，光伏及燃料电池等新能源以及特殊电机驱动系统等[1-3]。然而，由于在矩阵（周波）变换器功率环节采用了双向开关，其安全换流便成为该变换器大功率、实用化的技术关键。40年来一直是电力电子变换技术的研究热点之一[4-8]。

在以往的控制策略中，通常采用单沿调制的锯齿波，其垂直边很难理想化，占空比不能充分利用。其频谱特性及动态特性也不及双沿调制的三角波优越，SPWM的优点得不到充分发挥；另外，双向开关的两个门极也都是共用一个驱动信号，当同一个桥臂的两个双向开关动作不同步时会引起严重的电压过冲振荡，危及功率器件的安全。针对上述问题，本文提出了相应的改进策略：高频变压器一次侧的高频逆变环节产生占空比为0.5的高频高压双极性等宽方波，二次侧的矩阵变换器再将其变换为常规的SPWM 高频高压脉冲序列（矩阵变换器仍采用成熟的SPWM 方式，载波为三角波），经LC 滤波器后便可得到需要的正弦波输出。该方式保留了常规单相逆变器单极倍频等优点。矩阵变换器的双向开关则采用解耦分时驱动方式，可以消除共用一个驱动信号引起的电压过冲，无需识别负载电流的极性即可实现自然换流及ZVS、ZCS。

文中重点阐述了矩阵变换器的工作原理及解耦分时驱动的实现方法，并给出了仿真及实验结果，表明了方案的正确性。

2 矩阵变换器的新型控制策略

2.1 主电路拓扑

图1a 为电路框图，它由高频逆变器、高频变压器和矩阵变换器3 个功率环节组成。矩阵变换器为2×2 结构，在行与列的交叉处由双向开关将行与列连接起来。双向开关的构成方式如图1 所示，这种结构可以用两个RB-IGBT 直接代换。图1b 为电路原理图，为简化且不失一般性，LR 支路可认为是矩阵变换器输出滤波网络Lf、Cf及感性负载的等效负载。

图1 高频链矩阵式正弦波变换器Fig.1 Matrix sinusoidal converter with high frequency link

2.2 双向开关门极控制策略

矩阵式结构是为了适应高频逆变级输入的高频、高压正负交变双极性方波，其结构可以等效为正组逆变器和负组逆变器两组并联。当高频、高压方波的正半周输入时，正组逆变器工作；反之，负组逆变器工作。由于两组并联，当一组逆变器工作时，另一组逆变器被反向截止，并为工作逆变器提供续流通道。

矩阵变换器的开关频率是高频逆变器开关频率的两倍。所以在正组或负组逆变器的工作周期内，可将输入视作稳定的直流高压。两组逆变器“交替接力”地工作，矩阵变换器便可将高频逆变器输入的高频、高压方波变换为常规的SPWM 脉冲序列，经滤波后便可得到需要的正弦波输出。矩阵变换器解耦等效电路如图2 所示。

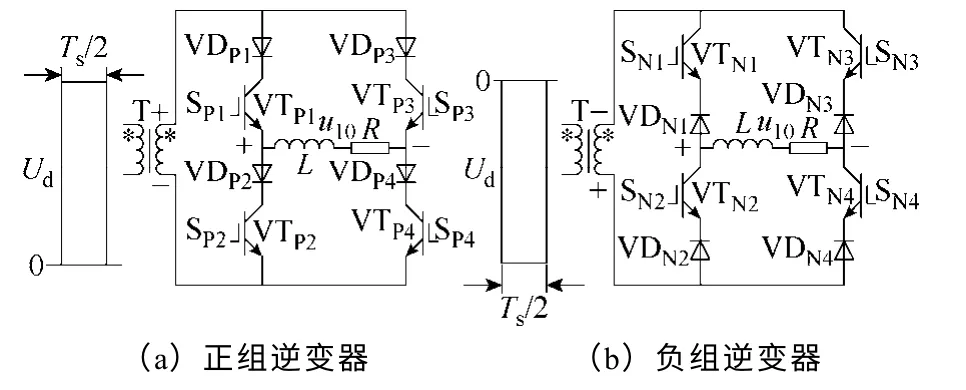
图2 矩阵变换器解耦等效电路Fig.2 Decouple equivalent circuits of MC

矩阵变换器双向开关函数Sij可定义为

式（2）为开关函数的约束条件，也是矩阵变换器驱动策略的依据。根据上述矩阵变换器的解耦原理及式（2）的约束条件，矩阵变换器中一个桥臂的4 路驱动信号逻辑表达式可写为

式中，SPWM1 为其中一路参考正弦与三角波载波相 比较得到的正弦脉宽调制信号；为其逻辑非；VP 是与高频逆变器驱动信号同频率，占空比为0.5且与VN 互为反相的方波。

以此类推不难得出另一桥臂驱动信号的逻辑关系。主要工作波形如图3 所示。

图3 高频链矩阵式正弦波变换器工作波形Fig.3 Working waveforms of matrix sinusoidal converter with high frequency link

3 矩阵变换器工作原理

3.1 工作模式分析

忽略功率器件的管压降，约定门极高电平开通，低电平关断。RL为感性负载，高频变压器一二次匝比为1，即Up=Us=UHV，Up、Us分别为高频变压器一二次电压。图4 所示为是将高频逆变器的一个工作周期分为10 个时段的工作波形，图5 所示为相应时段的等效电路。各工作模式分析如下。

图4 矩阵变换器工作波形Fig.4 Working waveforms of MC

t1之前，高频逆变器VT1、VT4导通，Us=UHV。SP1、SN1、SP3、SN3为高电平，VDP1、VTP1、VTN3、VDN3导通，负载电流i0续流，并线性下降。u10（未经滤波的负载两端电压）为零。VTP3、VTN1中无电流。

（1）工作模式1（t1～t2）。t=t1时，SP3为低电平，VTP3零流零压断开；SP4高电平，VTP4、VDP4导通，VTP1、VDP1（t1之前已开通）和正组逆变器工作，Us=u10=UHV。i0、is线性增加，负载获得能量。VTN3与VTP4换流不存在同步问题，因SN3自t1～t5始终为高电平，即使VTP4延迟导通，VTN3仍保持续流通道，待VTP4开通后再行换流，而后VTN3自然截止。类似情况以下不再复述。等效电路如图5a所示。

（2）工作模式2（t2～t3）。t=t2时，SP1为低电平，VTP1断开；SP2为高电平，VTP2导通。i0通过VDP4、VTP4、VDN2、VTN2续流，i0线性下降，u10为零。因t1之后SN2一直为高电平，所以VTP1与VTN2换流不存在同步问题。VTN2导通后，VTP2截止。等效电路如图5b 所示。

（3）工作模式3（t3～t4）。t=t3时，SP2为低电平，VTP2零流零压关断；SP1为高电平，VTN2截止，VTP1、VTP4导通，正组逆变器工作。u10=UHV，is、i0线性增长，负载获得能量。VTN2与VTP1换流同样不存在同步问题。等效电路如图5a 所示。

（4）工作模式4（t4～t5）。t=t4时，SP4为低电平，VTP4断开，i0沿VDN3、VTN3、VDP1、VTP1续流，i0线性下降，u10为零。SN2为高电平，VDN2截止。t4之前VTN3已开通，所以VTP4与VTN3换流也无同步问题。SP3虽为高电平，但VTP3被VDN3、VTN3截止。等效电路如图5c 所示。

图5 各工作模式等效电路Fig.5 Equivalent circuits of deferent work modes

（5）工作模式5（t5～t6）。在t=t5的邻域里，是高频逆变器的死区时间td（约1μs），变压器贮存的能量沿VD2、VD3向Ud反馈，随之VT2、VT3零电压导通。UP极性翻转。SP4为高电平，VTP4导通。SN3为低电平，VTN3零压截止；SP2为高电平，但由于UHV极性翻转，VTP2截止。SN1为低电平，VTN1零流零压截止。VTN3与VTP4换流情况同模式4，i0沿VDP4、VTP4、VDN2、VTN2续流，i0继续线性下降，u10为零。等效电路如图5d 所示。

（6）工作模式6（t6～t7）。t=t6时，SN4为低电平，VTN4零压零流截止；SN3为高电平，VDN2、VTN2、VDN3、VTN3导通，负组逆变器工作，u10=UHV。i0、is分别向正、负方向线性增长，负载获得能量。等效电路如图5e 所示。

（7）工作模式7（t7～t8）。t=t7时，SN2为低电平，VTN2截止；SN1为高电平，VTN1导通。因VTP1在t3之后一直导通，i0沿VDN3、VTN3、VDP1、VTP1续流，i0线性下降，u10为零。等效电路如图5f 所示。

（8）工作模式8（t8～t9）。t=t8时，SN1为低电平，VTN1零压零流截止；SN2为高电平，VDN2、VTN2、VDN3、VTN3导通，负组逆变器工作。u10=UHV。i0、is分别向正、负方向线性增长，负载获得能量。等效电路如图5e 所示。

（9）工作模式9（t9～t10）。t=t9时，SN3为低电平，VTN3截止。i0经VDP4、VTP4、VDN2、VTN2续流，i0线性下降，u10为零。等效电路如图5d 所示。

（10）工作模式10（t10～t11）。t=t10附近为高频逆变器的死区时间td，变压器储存的能量沿VD1、VD4向Ud反馈，随之VT1、VT4零电压导通；t=t10时，SN3为高电平，VTN3导通；SP4为高电平，VTP4导通。VTP4与VTN3换流。i0沿VDN3、VTN3、VDP1、VTP1继续续流并线性下降，u10为零。其他开关动作与t1之前相同。等效电路如图5f 所示。

t11之后重复上述工作模式。

3.2 控制策略及换流情况分析

（1）由以上分析知，在矩阵变换器的一个开关周期内，可以产生两个SPWM 脉冲波，等效开关频率提高了1 倍,经过数学推导可得[10]

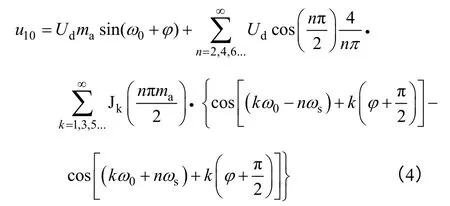
上式表明：基波分量为Udmasin(ω0+φ)，调节ma即可调节输出电压。谐波分量(kω0±nωs)，谐波振幅为，第一组谐波(2ωs±kω0)。式（4）与文献[9]中单相逆变器输出表达式一致，说明该方式保留了常规单相逆变器的倍频特性。

（2）矩阵变换器8 路驱动信号每一瞬间均有6路处于高电平，保证一组逆变器工作，另一组提供续流通道；另2 路为低电平，以阻止二次电压被短路。

（3）同一个双向开关的2 路驱动信号是分离（解耦）的，开通和断开是分时的。

（4）模式2、模式4、模式5、模式7、模式9、模式10 矩阵变换器为续流模式，其间动作的开关为ZVS、ZCS；其中模式5、模式10 还包括能量回馈模式，VT1～VT4为ZVS。

（5）模式1、模式3、模式6、模式8 为供电模式。起始时刻为t1、t3、t6、t8，终了时刻为t2、t4、t7、t9。功率开关虽为常规操作，但不会由于双向开关的不同步而引起高频变压器一二次及双向开关两端电压过冲。

各模式换流过程中，不存在由于采用同一个驱动信号双向开关的不同步而引起的电压过冲[1-8]，并可克服采用判别负载电流极性换流而导致负载电流过零点的畸变现象[5]。

4 仿真与实验

4.1 仿真分析

建立模型，主要仿真参数如下：Ud=300V，LF=300μH，CF=20μF，高 频 逆 变 器 开 关 频 率fs=10kHz，三角波载波频率fc=20kHz，调制频率fr=50Hz，感性负载L=10mH、R=40Ω，高频变压器匝比 1 1.27∶。输出 50Hz、220Vrms，视在功率为1kV•A。图6 所示为仿真波形。

其中图6a 为矩阵变换器输出电压U10（滤波前）及负载电压(滤波后)u0、电流i0波形，u0的总谐波含量(THD)＜1%。图6b 为双向开关S11两端电压波形。图6c 为变压器二次电压波形。图6d 为矩阵变换器输出电压u10展开后的波形细节。图6e 为高频变压器二次电流is的波形。图6b～6e 为同一时间坐标（波形底部）。图6f 为u10的频谱图。以上可以看出第一组谐波在40kHz 处，这证明了该方式保留了常规单相逆变器倍频的优点。从仿真波形可看出，由于采用了新型解耦分时驱动策略，各电压波形的前后沿干净，无电压过冲，软开关效果比较理想。

图6 仿真波形与频谱Fig.6 Waveforms and spectrum of simulation

4.2 实验研究

依照图 1b 所示的电路拓扑，构建了一台S=1kV•A 高频链矩阵式正弦波变换器。输入直流高压Ud=300V，开关频率 10kHz，三角波载波频率20kHz，幅度调制比ma=0.8，输出50Hz、220Vrms。高频逆变器和矩阵变换器功率开关分别选用Infineon 公司IGBT 单管IKW30N60T、SGW20N60及快恢复二极管IDD23E60。高频变压器铁心选用ONL644020 超微晶合金，一二侧匝比1 1.3∶。滤波电感、电容分别为400μH、20μF。感性负载L=15mH、R=40Ω。实验波形如图7 所示。可以看出，高频变压器一二次电压、双向开关（S11）两端电压及矩阵变换器的输出电压（u10）均无电压过冲毛刺。仿真与实验结果十分吻合，表明了新型解耦分时驱动策略有效地克服了双向开关的电压浪涌。

图7 实验波形Fig.7 Experiment waveforms

5 结论

本文提出的高频链矩阵式正弦波变换器双向开关两个门极解耦分时驱动及常规的SPWM 控制策略，不需要检测负载电流的极性，简单且易于实现。避免了负载电流过零点的畸变，实现了双向开关安全自然换流，有效地克服了电压浪涌；保留了常规单相逆变器的倍频特性，有利于滤波网络的小型化。仿真和实验都表明了分析的正确性和工程实现的可行性。对于超前功率因数的容性负载同样可以得到满意的效果，由于篇幅限制不便述及。总之，新型解耦分时驱动及SPWM 策略为该类变换器大功率、实用化提供了依据。

[1]Tian Feng,Alatrash H,Kersten R,et al.A single-staged PV array-based high-frequency link inverter design with grid connection[C].IEEE Conference on Industrial Electronics and Applications,2006:1451-1454.

[2]Ma Xianmin.Analysis and design of PDM converter with high fre-quency link for HEV drive system[C].IEEE International Power Electronics and Motion Control Conference 2006:1928-1931.

[3]Zhu Li,Zhou Keliang,Zhu Wenjie,et al.High frequency link single-phase grid-connected PV inverter[C].IEEE ISPEDGS,2010:133-137.

[4]Tang Difei,Li Lei.Analysis and simulation of push-pull three level AC-AC converter with high frequency link[C].14th IEEE Conference on Industrial Electronics and Applications,2009:3366-3371.

[5]Chen Daolian.Novel current-mode AC-AC converters with high-frequency AC link[J].IEEE Transactions on Industrial Electronics,2008,55(1):30-37.

[6]De D,Ramanarayanan V.A proportional+multiresonant controller for three-phase four-wire high-frequency link inverte[J].IEEE Transactions on Power Electronics,2010,25(4):899-906.

[7]Li Hui,Li Xiaobing,Hu Tianyou.Simulation of SPWPM high-frequency link inverter for EPS[C].Proceedings of IEEE Mechatronics and Automation,2008:1106-1110.

[8]吴胜华,钟炎平,权建洲.高频链矩阵式正弦波变换器研究[J].电力电子技术,2010,44(9):11-13.Wu Shenghua,Zhong Yanping,Quan Jianzhou.Research on matrix sinu-soidal waveforms converter with high frequency link[J].Power Electronics,2010,44(9):11-13.

[9]De D,Ramanarayanan V.A DC-to-three-phase-AC high-frequency link converter with pensation for nonlinear distortion[J].IEEE Transaction on Industrial Electronics,2010,57(11):3699-3677.

[10]曹立威,吴胜华,张成胜,等.SPWM 谐波分析的一般方法[J].电力电子技术,2002,36(4):62-65.Cao Liwei,Wu Shenghua,Zhang Chengsheng,et al.A general method of SPWM harmonic analysis[J].Power Electronics,2002,36(4):62-65.