永磁-感应子式混合励磁发电机三维暂态温度场的计算与分析
付兴贺 林明耀 徐 妲 房淑华
(东南大学电气工程学院伺服控制技术教育部工程研究中心 南京 210096)
1 引言
混合励磁发电机既有永磁电机体积小、效率高的特点,又具有电励磁电机输出电压可调的特性,近年来混合励磁电机的研究不断涌现。但是,关于混合励磁电机温度场的研究则相对较少,仅查到文献[1]分析了混合励磁同步电机安全运行的温升极限问题,文献[2]建立了混合励磁磁通切换电机的三维温度场计算模型。永磁-感应子式混合励磁发电机(PM-IHEG)内的热源较多,影响热源的因素较为独特,对该电机进行温度场计算,揭示电机内的温度场分布规律,对掌握该电机的运行特性以及优化设计具有重要的意义。
目前,有限元法是研究电机温升问题的常用方法[3,4]。文献[5-7]采用有限元法对永磁电机的温度场进行了计算与分析,取得了大量有意义的结论,验证了有限元方法在计算电机温度场时具有较高的计算精度。
本文建立了电磁稳态条件下PM-IHEG 三维暂态温度场的求解模型,给出了基本假设和边界条件,确定了相关部件的导热系数及表面散热系数,采用三维有限元法对电机的暂态温度场进行了计算,分析了相关因素对电机温度场的影响,并进行了实验验证。
2 永磁-感应子式混合励磁发电机的结构
所研究的PM-IHEG的结构如图1 所示。
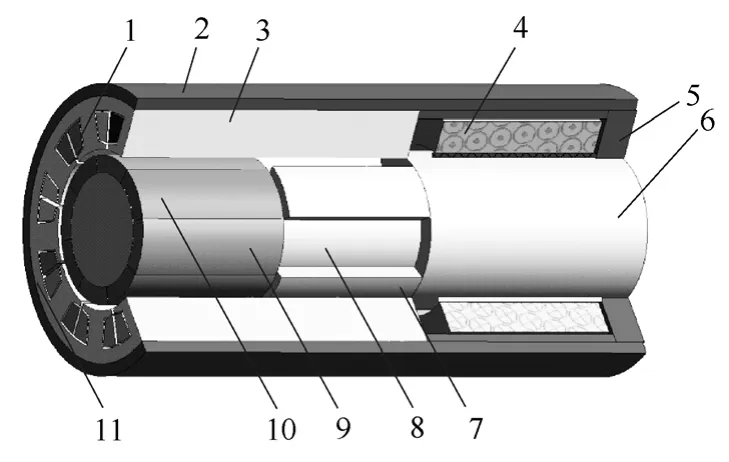
图1 PM-IHEG的结构示意图Fig.1 Structure diagram of the PM-IHEG
PM-IHEG 由永磁部分和感应子部分组成,永磁部分位于电机中部,感应子部分位于电机两端。电机的定子铁心采用传统的叠片式结构,电枢绕组为三相对称绕组,永磁部分和感应子部分共用一套定子铁心和电枢绕组。电机永磁部分的转子为表贴磁钢结构,感应子部分电枢绕组所对应的转子为齿槽凸极结构,齿槽数等于电机极对数,齿槽中心线与永磁体中心线重合。两部分转子间留有一定间隔,以减少磁路耦合。环形励磁绕组放置在电枢绕组与端盖之间,通过励磁绕组支架与电机机壳相连,励磁绕组的中心线与定子铁心及转轴的中心线重合。
3 温度场数值计算基础
3.1 求解区域及边界条件
考虑PM-IHEG 几何结构的对称性,以轴向二分之一及周向二分之一电机为研究对象,确定电机三维温度场的求解区域如图2 所示。
根据传热学理论,暂态运行时电机内的三维温度场所满足的导热微分方程可描述为


图2 PM-IHEG 三维温度场的求解区域Fig.2 Solved region of the temperature field computation of the PM-IHEG
电机各部分的边界面上,满足如下边界条件

式中T——温度(℃);
TW——已知壁面温度(℃);
T0——周围介质的温度(℃,时间的函数);
q——热源密度(W/m3);
q0——通过边界面的热流密度(W/m3);
c——比热容(J/(kg·℃));
γ——密度(kg/m3);
t——时间(s);
α——散热系数(W/(m2·℃));
Ai(i=1,2,3)——第i类边界条件的物体边界;
λn——边界面的法向导热系数(W/(m·℃));
λx,λy,λz——各介质x、y、z方向的导热系数(W/(m·℃))。
本文所研究的求解域内各个物质边界上的传热和散热边界条件如下:
(1)对于电机内温度场定解问题的研究,不存在第一类边界。
(2)第二类传导散热边界条件为:边界上热传导的热量为q0,即边界的法向温度梯度已知。当q0=0时,此面上无热传导,为绝热边界条件。在PM-IHEG温度场的求解区域中,符合绝热边界条件的边界面包括电机的轴向对称面和周向对称面。考虑电机结构的对称性,电机轴向中间断面S1为绝热面,即断面S1上满足如下边界条件

考虑电机结构的对称性,电机周向二分之一处的断面S2为绝热面,即断面S2上满足如下边界条件:

(3)第三类对流换热边界条件为:边界上从物体内部传到边界上的热流量与通过该边界散失到周围介质中的热流量相等。在PM-IHEG 温度场的求解区域中,满足第三类边界条件的边界面包括图2中的S3~S10。
3.2 导热系数及散热系数的确定
3.2.1 导热系数的确定
考虑求解区域中导热体几何形状的不规则性,可用等效导热系数来描述各导热体的传热性能[8]。
(1)定子铁心的导热系数。电机的定子铁心由硅钢片叠压而成,铁心沿轴向的热传递可以等效为多层平壁的串联,沿径向导热可以等效为多层平壁的并联。因此,定子铁心的轴向导热系数要比径向导热系数小得多。
(2)绝缘材料的导热系数。电机中的绝缘部分常由多种材料组合而成,各种材料也并非完全均质,而且绝缘材料各层间存在一定空隙,因此,宜采用等效导热系数来描述定子铁心槽内绝缘材料的传热效果。将定子铁心槽内绕组(包括漆膜、绕组间的浸渍漆及空气层)等效为两个导热体;槽内的绝缘材料(包括浸渍漆、槽绝缘、层间绝缘以及空气层)等效成一个导热体,等效前后槽内绕组的分布如图3 所示。
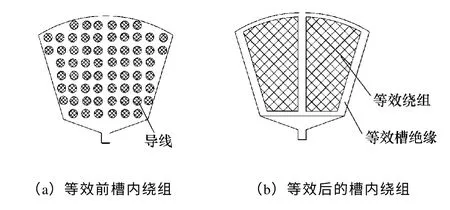
图3 等效前后槽内的绕组排列Fig.3 Armature winding arrangements before and after equivalent transformation
(3)电枢绕组的导热系数。将电枢绕组等效成导热体,等效导热体沿绕组绕制方向为热的良导体,在其他方向上受导线漆膜以及绕组间残留气隙的影响导热性能下降,等效导热体仍然具有各向异性的特点,可参考文献[9]计算等效导热体的导热系数。
电枢绕组在端部位置处绕制方向发生变化,求解域中电枢绕组直线段和绕组端部的坐标系分别选用相互独立的直角坐标系和圆柱坐标系,直线段的轴向导热系数等于绕组线芯的导热系数,绕组端部圆周方向的导热系数等于绕组线芯的导热系数。
(4)励磁绕组的导热系数。参照电枢绕组及铁心槽绝缘的导热系数的确定方法,计算励磁绕组和绝缘材料的等效导热系数。电机感应子部分的励磁绕组为与转子同轴的环形绕组,在圆柱坐标系下描述励磁绕组各个方向上的导热系数,考虑导线漆膜、绕组间残留空气及浸渍漆对励磁绕组导热系数的影响,励磁绕组仍然可按各向异性来处理。励磁绕组绕制方向上的导热系数等于绕组线芯的导热系数。
(5)定转子间气隙的等效导热系数。电机定转子间的换热过程包括对流和热传导,可引入等效导热系数的概念,用静止流体的导热系数来等效描述流动介质的换热能力[10]。当电机定转子间的气隙区域为环形时,若流体的雷诺数小于临界雷诺数,热量是通过纯热导由一个表面传递到另一个表面,并且热交换强度与电机转速无关,此时可认为气隙的等效导热系数λδeff等于气隙介质的导热系数λδ;若流体的雷诺数大于临界雷诺数,则此时气隙的等效导热系数可按如下公式计算:
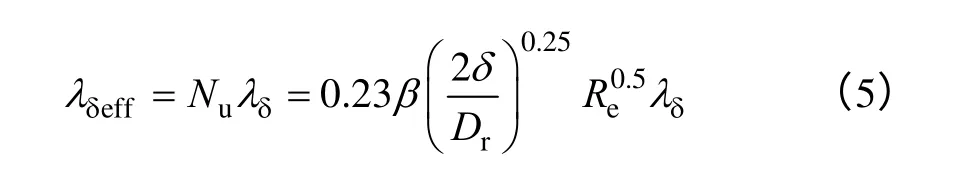
式中Nu——气隙中的努塞尔数;
β——考虑转子表面粗糙度的经验系数,β取值为1.15~1.25;
δ——气隙长度(m);
Dr——转子外径(m);
Re——气隙中的雷诺数。
当定转子表面开槽时,在离心力的作用下,临界雷诺数比定转子壁面均是圆筒时的临界雷诺数低得多,此时气隙内的努塞尔数Nu可表示为
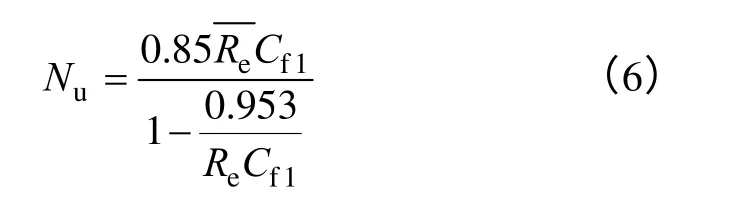
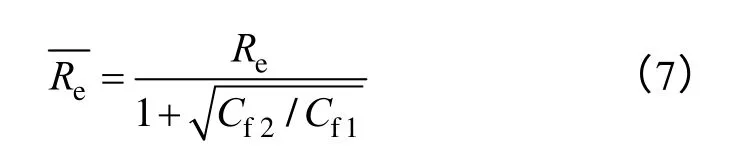
式中Cf1,Cf2——定转子表面的摩擦阻力系数。
当定转子表面的粗糙度相同时,可按下式计算摩擦阻力系数
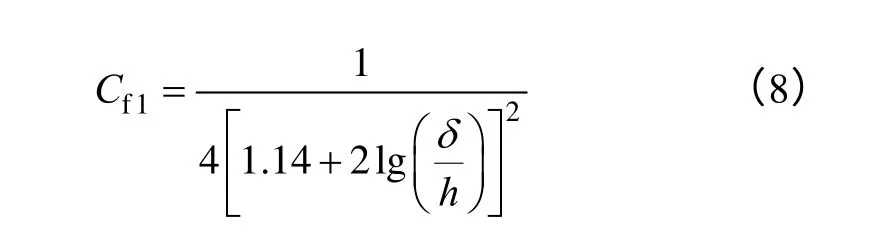
式中h——转子表面上的突起高度(m)。
基于以上分析,可计算出定转子间气隙的等效导热系数。
3.2.2 散热系数的确定
电机表面散热系数与很多因素有关,如导热系数、动粘系数、流体的速度、密度以及比热容等,这些物理量之间的关系比较复杂,可以根据经验并结合实验的方法来确定电机各部件的表面散热系数。PM-IHEG的表面散热系数包括铁心端部表面散热系数、转子端部表面散热系数、机壳外表面散热系数、端盖散热系数等,这些系数可参考普通电机散热系数的计算方法来确定。
3.3 热源的确定
PM-IHEG 内的热源主要包括铁心损耗、电枢绕组铜耗、励磁绕组铜耗、永磁体涡流损耗、凸极转子涡流损耗以及机械损耗。受材料特性的影响,电机中的各种损耗在电机运行过程中是时刻变化的,为简化计算,忽略各种损耗的时变特性,即不考虑温度变化引起的电机电磁性能及热源的变化,只考虑温度的平均效应。
4 三维暂态温度场的数值计算与分析
PM-IHEG 三维暂态温度场的分布与电机工作状态有关,下面分别讨论。
4.1 励磁电流对暂态温度场的影响
以发电机空载运行为例,当励磁电流为零时,电机的热源主要为永磁部分的铁心损耗,随着励磁电流的增加,电机内的热源主要包括永磁部分的铁心损耗、感应子部分的铁心损耗以及励磁绕组铜耗。在额定转速下,当励磁电流为零以及额定电流时,发电机的温度场分布如图4 所示。

图4 不同励磁电流时电机内的温度场分布Fig.4 Temperature field with different excitation currents
计算结果表明,当励磁电流为零时,电机内的温度场沿轴向方向的变化梯度较大,永磁部分与电机端部最热点的温差约10℃。在额定励磁电流的作用下,电机端部的温度升高了近10℃,励磁绕组的温度升高了近15℃。原因在于,尽管电机感应子部分磁场的交变分量小于永磁部分磁场的交变分量,但受直流偏磁的影响,电机感应子部分的铁心损耗增加较多,故感应子部分温度上升的幅度较大。
不同励磁电流时,发电机励磁绕组的温升变化如图5 所示。励磁电流不同时,铁心损耗和励磁绕组铜耗不同,所以励磁绕组温升曲线的拐点出现的时间不同。随着励磁电流的增加,励磁绕组的稳定温升呈非线性的增加。一方面是由励磁绕组铜耗随励磁电流的变化趋势所决定的,另一方面是受电机轴向导热的影响。
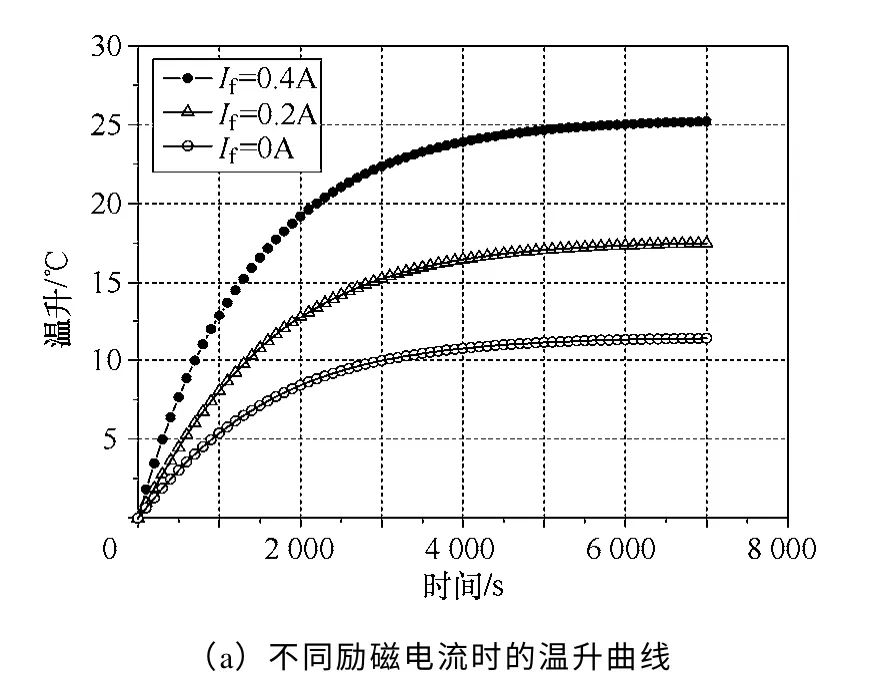
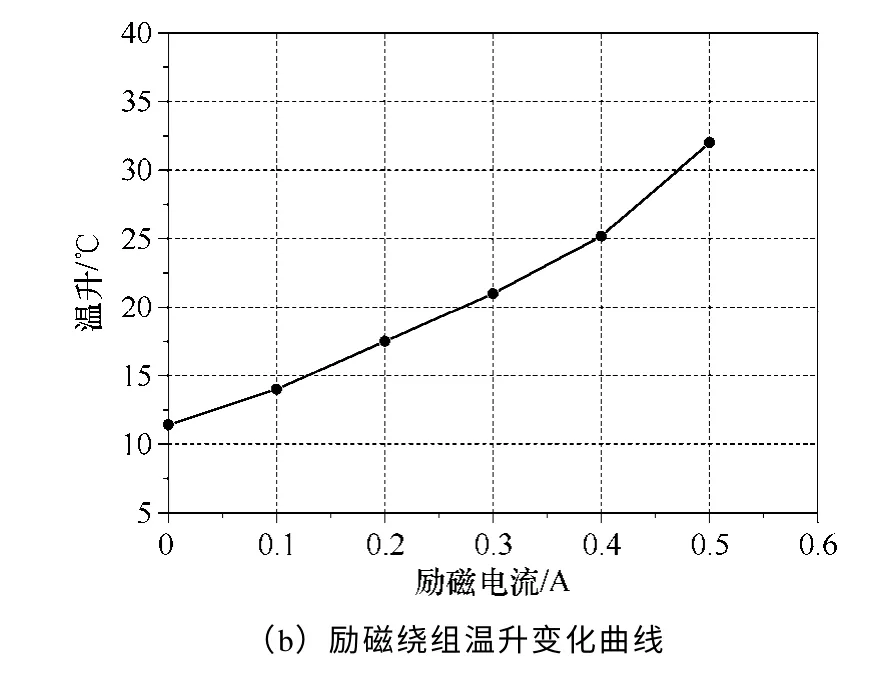
图5 励磁电流对励磁绕组稳定温升的影响Fig.5 Influence of the excitation current on stable temperature rise of the excitation coil
4.2 电机转速对电机温度场的影响
额定励磁电流作用下电机空载运行,此时电机内的热源主要包括永磁部分的铁心损耗、感应子部分的铁心损耗以及励磁绕组铜耗。
不同转速时电机定子铁心和励磁绕组的温升曲线如图6 所示。可见电机转速的增加不仅使得定子铁心的稳定温升增加,而且受轴向传热及空间散热的影响,励磁绕组的稳定温升也有所增加,但增加的幅度相对较小。

图6 不同转速时的温升曲线Fig.6 Temperature rise with different speeds
定子铁心和励磁绕组的稳定温升随电机转速的变化曲线如图7 所示。随着电机转速的增加,定子铁心的稳定温升增加较快,励磁绕组的稳定温升增加较慢。原因在于:尽管电机转速增加的同时,励磁绕组的铜耗不变,但受电机轴向导热的影响,励磁绕组的稳定温升也有所增加。

图7 电机转速对电机稳定温升的影响Fig.7 Influence of the speed on the stable temperature rise
4.3 负载类型对电机温度场的影响
发电机带三相对称负载和整流负载时,电机内的定子铁心损耗、绕组铜耗以及转子涡流损耗存在差异,这种差异将影响电机的温度场分布。在额定转速、额定励磁电流及输出功率相同的前提下,带三相对称负载与整流负载时电机主要部件的温升曲线如图8 所示。
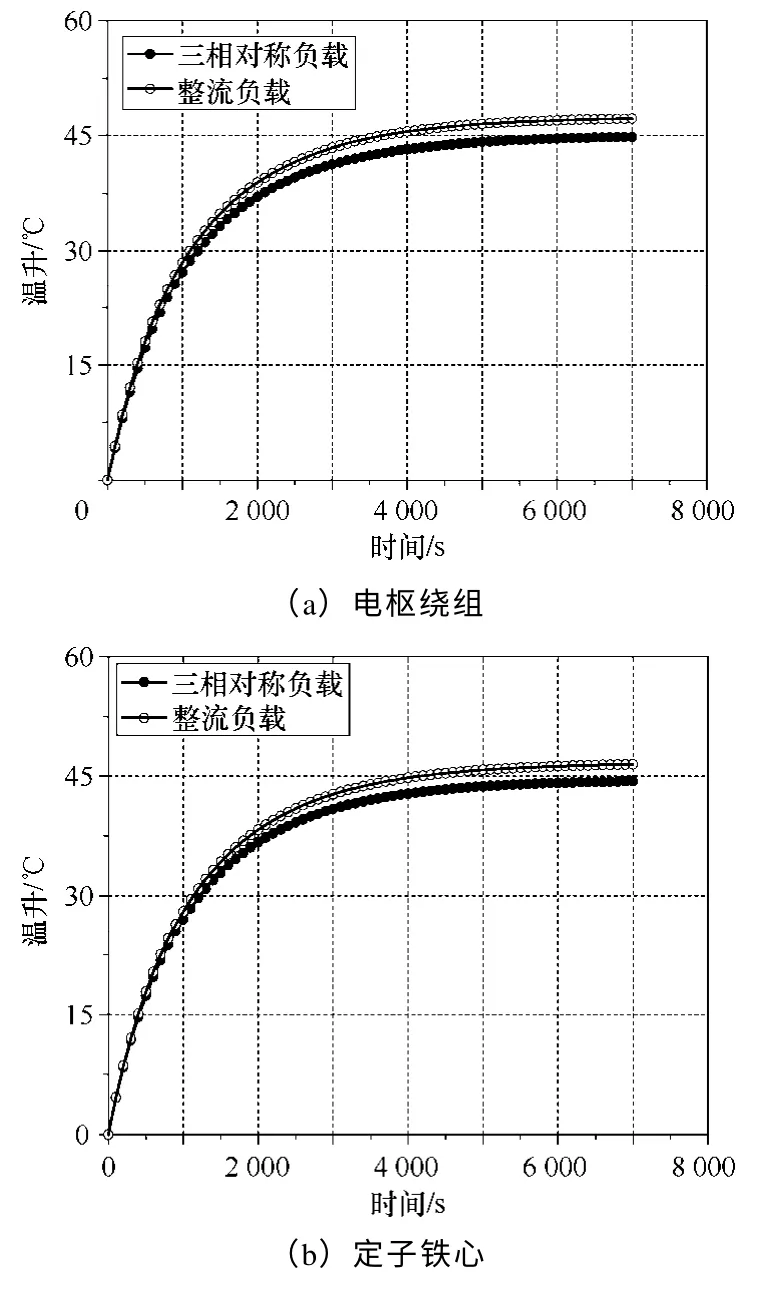
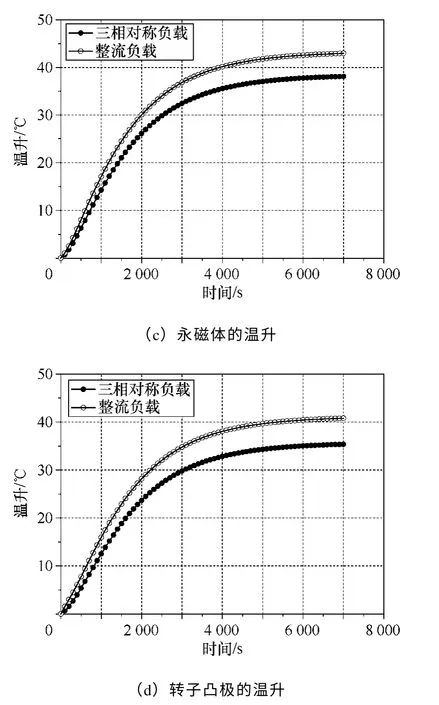
图8 负载类型不同时电机的温升曲线Fig.8 Temperature rise with different loads
可以看出,带整流负载时电机主要部件的稳定温升高于带三相对称负载时的情况,尤其是永磁体和感应子部分的转子凸极,两种负载下两者的稳定温升相差约7℃。原因在于,带整流负载时,发电机电枢绕组的谐波电流产生的谐波磁场在永磁体和感应子部分转子凸极表面产生较大的涡流损耗,进而导致电机转子的发热严重。
5 实验
根据电磁计算结果设计并制作PM-IHEG 样机如图9 所示。在样机绕组、机壳、端盖等部件的表面放置温度传感器用来测量温度。用原动机拖动样机在不同工况下运行,进行相关温升实验。

图9 PM-IHEG 样机Fig.9 PM-IHEG prototype
励磁电流为零时,机壳温升曲线的实验结果和有限元计算结果如图10 所示。可见,机壳表面温升的计算结果与实验结果基本吻合,两者最大相差4℃。
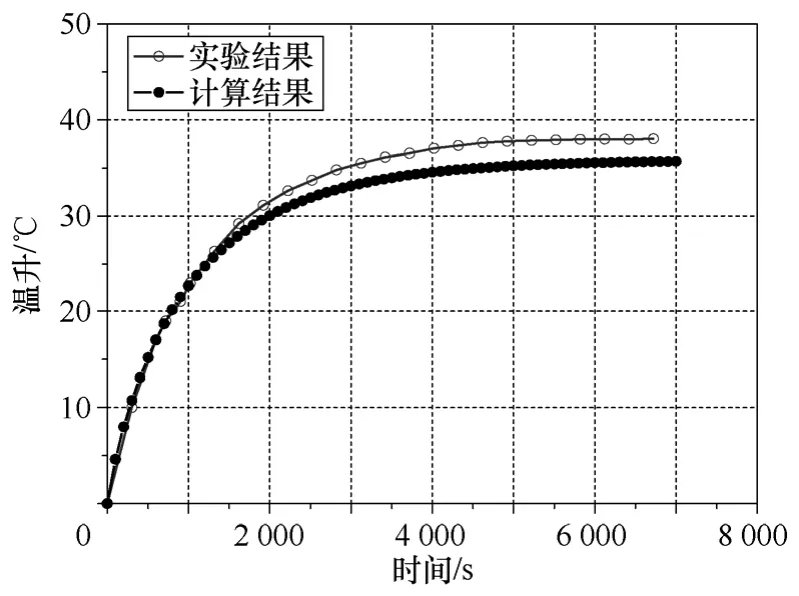
图10 机壳温升曲线的计算结果与实验结果Fig.10 Comparison of the temperature rise of cabinet
在额定转速及额定励磁电流条件下,带纯阻性的整流负载运行时,发电机机壳及电枢绕组温升曲线的实验结果和有限元计算结果如图11 所示。负载运行时发电机机壳表面及电枢绕组的温升计算结果与实验结果存在一定偏差,分析原因可能在于导热系数及散热系数的偏差所引起的。

图11 样机温升曲线的计算结果与实验结果Fig.11 Comparison of the temperature rise of PM-IHEG between calculation and experimental results
总体而言,PM-IHEG 三维暂态温度场的计算结果与实验结果比较接近,文中所选取和计算的导热系数、散热系数以及热源、求解模型等基本正确。所做的研究工作为PM-IHEG的电磁设计和性能优化奠定了基础。
6 结论
本文建立了PM-IHEG 三维暂态温度场的计算模型,对电机内的温度场进行了计算与分析,得到以下结论:
(1)揭示了不同工况下PM-IHEG的温度场分布规律及最大温升位置,获得了各部分元件的温升变化曲线。
(2)温度场计算结果与实验结果基本吻合,验证了文中所用的散热系数、导热系数、热源及计算方法的正确性。
(3)当设计PM-IHEG 时,应考虑以下特点:额定励磁电流时,电机中感应子部分的温升超过永磁部分;带整流负载时电机的温升高于带三相对称负载时的情况。
[1]Fodorean D,Miraoui A.Permanent magnets thermal operation limits in a hybrid excited synchronous machine used on wide speed applications[C].IEEE International Conference on Optimization of Electrical and Electronic Equipment,Brasov,Romania,2008:21-26.
[2]Hoang E,Lecrivain M,Gabsi M.3-D thermal model of an hybrid excitation flux switching synchronous machine using a 2-D FE method software[C].International Symposium on Power Electronics Electrical Drives Automation and Motion,Pisa,Italy,2010:101-104.
[3]Kolondzovski Z.Determination of critical thermal operations for high-speed permanent magnet electrical machines[J].International Journal for Computation and Mathematics in Electrical and Electronic Engineering,2008,27(4):720-727.
[4]Gerada D,Mebarki A,Mokhadkar R P,et al.Design issues of high-speed permanent magnet machines for high-temperature applications[C].IEEE International Electric Machines and Drives Conference,Miami,FL,USA,2009:1036-1042.
[5]Jiqiang W,Fengxiang W,Xiaoguang K.Losses and thermal analysis of high speed PM machine[C].International Conference on Power System Technology,New Delhi,India,2008:1-5.
[6]Aldo Boglietti,Andrea Cavagnino,David Staton,et al.Evolution and modern approaches for thermal analysis of electrical machines[J].IEEE Transactions on Industrial Electronics,2009,56(3):871-882.
[7]李俊卿.采用混合单元的汽轮发电机定子温度场的分析与计算[J].中国电机工程学报,2009,29(18):78-82.Li Junqing.Analysis and calculation on temperature field of turbo-generators with dual elements[J].Proceedings of the CSEE[J].2009,29(18):78-82.
[8]Kyle A Brucker,Joseph Majdalani.Equivalent thermal conductivity for compact heat sink models based on the churchill and chu correlation[J].IEEE Transactions on Components and Packaging Technolo-gies,2003,26(1):158-164.
[9]胡敏强,黄学良.电机运行性能数值计算方法及其应用[M].南京:东南大学出版社,2003.
[10]Kwon O.Analysis and experiment on the thermal characteristics of electric motors[D].Berkeley:University of California,2001.

