基于预测无差拍算法的永磁同步发电机无传感器控制

童 力 邹旭东 丰树帅 黄清军 张 允 康 勇

（1.华中科技大学强电磁工程与新技术国家重点实验室 武汉 430074 2.湖南省电力公司供电服务中心 长沙 410007）

1 引言

风能因其可大规模开发和无污染利用，而被广泛视作传统化石能源发电应用的替代能源[1,2]。当前，主流的风力发电技术包括双馈式和直驱式，而适应更低转速[3]的永磁同步发电机（PMSG）使直驱式风力发电系统在省却齿轮箱的同时，呈现出高效、可靠以及出色的电网故障适应性[4,5]，因而极具应用前景。为实现PMSG的高效运行，常用光电编码器或旋转变压器为其高性能矢量控制提供精确的转子位置和转速信息。但随着风电机组功率等级和机械尺寸的提升，机械式传感器变得难以安装且极易受工作环境干扰，运行可靠性大幅降低、甚至会影响到发电机组的安全与稳定运行。为此，研究PMSG的无传感器控制技术具有十分重要的理论意义和工程应用价值[6,11]。

永磁同步发电机的无传感器控制需要观测转子的位置和转速，来参与发电机的磁场定向与速度反馈控制。一方面，基于高频信号注入的观测方法[6]利用电机的凸极效应在转速低至零时仍可实现观测，但局限于凸极电机，且额外引入的高频信号会降低电机的控制性能。另一方面，基于反电动势的观测方法[7,9]，其本身具备出色的动静态性能，但在极低转速时难以满足观测精度。考虑到实际风力机组仅在切入风速以上发电运行，PMSG 无需零速启动且不会运行在过低的转速区域，本文提出基于估算反电动势的同步锁相环（SRF-PLL）技术[10,11]，来观测转子的位置角和转速以实现无传感器控制。

一般地，反电动势的估算精度依赖于电机模型参数和定子电流的跟踪控制性能，并影响着PMSG无传感器控制的整体性能。在数字控制系统中，由电流采样、占空比更新和死区等因素引起的控制延迟[12]，会降低系统的控制性能，而电机参数的变化会使性能进一步恶化。为此，需要有效的定子电流环控制方案，以适应控制延迟和参数时变对控制性能造成的影响。目前，PMSG的电流控制方法主要包括：滞环控制、同步旋转坐标系下的PI 控制和预测控制。滞环控制实现简单、动态性能好[13]，但开关频率不确定且存在较大的电流跟踪误差。同步旋转坐标系下的PI 控制具有出色的稳态跟踪性能，但受制于带宽限制、动态性能较差，需要额外的延时补偿来提高电流环的性能[12,14]。相比较而言，预测控制可以得到更出色的动态响应和稳态跟踪性能。其中，基于目标函数直接确定变换器开关动作的直接预测控制[10,15,16]，电流响应速度快，但较高的实时性要求和受效率限制的开关频率降低了其控制性能，会产生较大的电流纹波；而根据预测方程得到电流跟踪所需的电压指令，并结合空间矢量调制（SVPWM）技术将电压指令转换成开关状态的无差拍控制[17-19]，可有效减少算法对实时性的要求，并具有较好的动态性能和较小的电流纹波。

本文在建立永磁同步发电机数学模型的基础上，利用电流控制器生成的定子电压指令实现反电动势的估算后，给出了基于SRF-PLL的转子位置与转速的观测模型。为了获得优异的无传感器控制性能，本文提出了一种预测无差拍控制算法：通过对估算反电动势进行串联补偿再引入到无差拍控制器中，改善系统稳定性的同时，实现了定子电流的无静差跟踪；在此基础上，基于Luenberger 算法对定子电流超前预测以补偿数字控制一拍滞后的影响，并在维持系统稳定性的前提下，根据离散控制模型设计控制器参数，改善了定子电流环的动态响应及其适应电机参数变化的鲁棒性。最后，通过仿真和实验证明了本文所提控制方案的有效性及其在实际风力发电应用中的可行性。

2 系统拓扑与数学建模

2.1 系统拓扑结构

基于永磁同步发电机的直驱式风力发电系统结构如图1 所示。风力机与PMSG（表贴式或内置式）同轴相连，并通过由公共直流环节耦合形成背靠背结构的并网变流器连接至电网。通常，只有当检测到预设的切入风速时，接触开关K1导通，并同时启动机侧变换器（Generator Side Converter,GSC）对PMSG 实施相应的控制策略进行风能捕获。与此同时，经由LC 滤波器和隔离变压器连接于电网的网侧变换器（Network Side Converter,NSC）则始终维持直流母线电压的恒定，以实现高质量的电能传输以及所需的无功补偿。本文将针对直驱风力发电系统中PMSG的无传感器控制技术进行理论分析和实验研究。

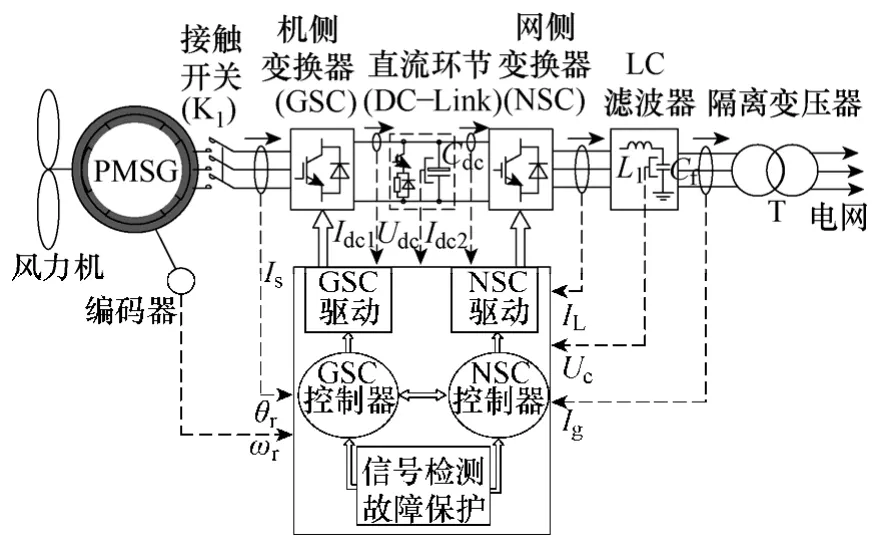
图1 基于永磁同步发电机的直驱风力发电系统结构Fig.1 System structure of PMSG-based driect-driven wind power generation system

2.2 PMSG的离散域数学模型

一般地，永磁同步发电机的高性能矢量控制是在转子位置角参与同步定向的旋转坐标系下实施的。取定子电流矢量为Is(t)=[Isd(t)Isq(t)]T，反电动势矢量为Es(t)=[Esd(t)-Esq(t)]T以及定子端电压矢量为ur(t)=[urd(t)urq(t)]T，式中下标d 和q 表示在旋转坐标系下所对应的状态量。于是，选择定子电流为状态变量，得到PMSG 在同步定向后的连续域状态空间模型为

式中ωr——转子的电气角速度；

Rs——定子相电阻；

Ld，Lq——交、直轴同步电感。

忽略数字采样过程中的延迟，由式(1)求解出连续时间状态的定子电流可表示为

取离散采样时间分别为t0=kTs和t=(k+1)Ts，可以得到离散时间状态的定子电流为

式中，“k”代表离散的采样时间点，k=1,2,3,…,n。

在系统采样周期Ts较小的情况下，同步旋转坐标系中的反电动势矢量Es和定子端电压矢量ur在kTs～(k+1)Ts的时间间隔内可近似视作恒定，于是

联立式（3）～式（5）并结合泰勒级数展开式，得到PMSG 离散域状态空间模型如下：

于是，根据式（6）可以执行基于电机模型的反电动势估算，以实现转子位置角和转速的观测。

3 基于SRF-PLL的无传感器观测算法

当PMSG 在永磁体磁场定向的参考坐标系下采取“零d 轴电流控制”策略时[20]，电磁转矩与定子q 轴电流间的正比例关系将使得发电机呈现出如直流电机般出色的控制性能。因此，无传感器控制方案的实现，首先需要观测转子的位置角。图2 所示为实际磁场定向的γ-Δ参考坐标系与观测的d-q 轴参考坐标系的空间矢量图。其中，两个旋转坐标系分别以电气角速度ωr和ωe旋转。

图2 实际与观测的同步定向坐标系空间矢量图Fig.2 Space vector diagram with actual and observed synchronized orientation frames

图2 中，θr和θe分别代表着实际的和观测的转子位置角。初始阶段，两者间存在一定的角度误差（即Δθ≠0）。此时，观测定向参考坐标系下的d-q轴反电动势Esd和Esq，实际是由永磁体磁通量ψf所确定的反电动势空间矢量投影所得，因而可得到其d 轴分量Esd与观测误差角Δθ之间近似相等的关系。因此，可将Esd作为同步锁相环的反馈输入，并通过 PI 控制器来调节观测输出的转子位置角θe，使Esd趋近于零（即Δθ≈0），实现转子信息的无传感器观测。为了避免直接采样PWM 波形状的定子端电压，本文利用电流控制器生成的电压指令来参与基于电机模型的反电动势估算。于是，在观测定向的d-q 坐标系下，基于电机模型参数新生成的系数 矩阵Jm和1m-H，得到估算的反电动势矢量如下：

式中，“m”定义为测量的与实际电机参数间的比值，即m=Lm/L=Rsm/Rs。

取式（7）中的d 轴分量Esd作为反馈，并进一步将基于q 轴反电动势Esq的前馈控制量式（8）叠加至PI 控制器的输出。最终，得到观测的转子电气角速度，如式（9）所示。

式中Kp和KI——锁相环PI 控制器的比例和积分 控制系数；

ΔEsd——d 轴反电动势的估算误差。

事实上，基于式（9）的观测转速已包含转子的位置角信息，但也同时存在着高频噪声[10]。为此，常采用低通滤波器（LPF）滤除式（9）中的高频分量后再对其进行积分运算，得到转子位置角观测的离散状态表达式为

根据式（7）～式（10），可以得到基于反电动势估算、采用SRF-PLL的无传感器观测模型，如图3 所示。当选取适当的PI 控制器和低通滤波器参数，便可有效地改善该观测方法的动态响应、扰动抑制能力及其他系统响应特性[10]。

图3 基于SRF-PLL的无传感器观测模型原理框图Fig.3 Block diagram of SRF-PLL based sensor-less observation model

尽管锁相环本身具备出色的动态响应特性，但转子位置角的观测很大程度上还将由反电动势的估算精度所决定。通过与精确磁场定向和无静差定子电流跟踪控制下的参考反电动势相比较，近似得到观测误差角Δθ的表达式为

式中，上标“*”表示参考指令值。

通过式（11）可以看到，在基于反电动势估算的SRF-PLL 无传感器观测方法中，转子位置角的观测精度是由电机模型参数和定子电流的跟踪控制所决定，而转子的位置角与其转速紧密相关。因此，在准确测量电机参数的前提下（即m=1.0 时），定子电流出色的静态跟踪特性（即）将能够实现观测误差的最小化控制。

4 鲁棒的预测无差拍电流控制

期望在下个控制周期(k+1)Ts结束之前实现电流指令跟踪的无差拍控制器，无疑将使无传感器控制的PMSG 呈现出优异的动静态响应特性。首先，为了实现定子电流的无静差跟踪，引入式（7）中的估算反电动势，并由此得到当前时刻kTs的电压控制指令表达式为

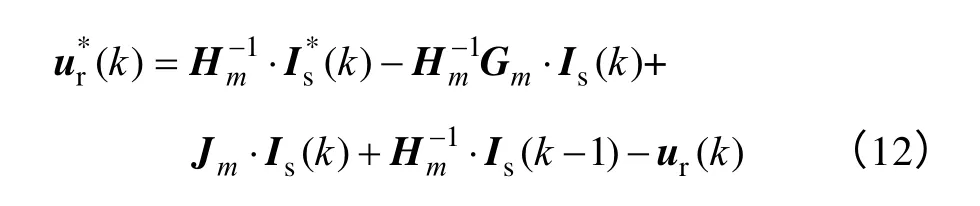
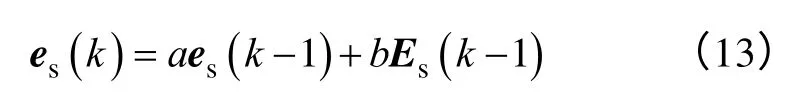
式中，a和b是串联补偿器的控制系数。

于是，由式（12）、式（13）可得到新的无差拍电压控制指令为

考虑数字控制的一拍滞后，基于式（7）、式（13）和式（14）可得到如图4 所示的采用串联补偿器的无差拍控制系统模型。

图4 带有串联补偿器的无差拍控制系统模型Fig.4 Model of dead-beat algorithm based control system with the cascade compensator

图5 有、无串联补偿器的无差拍控制系统闭环特性分析Fig.5 Closed-loop characteristics of dead-beat control based system with or without compensator

在不考虑电机参数变化的前提条件下（即m=1.0 时），串联补偿前、后的无差拍控制系统闭环特性如图5 所示。图5a 中，补偿前的系统闭环主导 极点处在远离单位圆之外的位置，而补偿后的主导极点将回到单位圆内。但此时系统的主导共轭极点十分靠近单位圆，这意味着恶劣的动态响应以及匮乏的稳定裕度。此外，如图5b 中系统的闭环频率响应特性所示，尽管能够在低频段实现零增益、零相移的控制特性，但额外引入的谐振峰还可能在定子电流中产生一定谐波分量，进而造成电机控制性能的下降。

通过上述分析可知，需要补偿滞后一拍对电流环动、静态响应特性的影响，尤其是当电机参数发生变化时，进一步提高PMSG 无传感器控制的鲁棒性。为此，在对估算反电动势引入串联补偿器的基础上，本文基于Luenberger 算法[19]对定子电流进行一拍超前预测，得到预测电流的表达式为

式中，系数D定义为预测权值，并设定在[0,1]的范围内变化。

将超前预测的定子电流Is(k+1)代入式（14）中，得到基于预测无差拍算法的电压控制指令为

同样地，结合式（7）、式（13）和式（16），在观测的d-q 参考坐标系下，可以进一步得到基于预测无差拍算法的系统控制模型，如图6 所示。

图6 基于预测无差拍控制算法的系统模型Fig.6 Model of predictive dead-beat algorithm based control system

通过离散传递函数的推导，可知图6 中所示的控制模型是一个四阶系统，其响应特性很大程度上是由预测权值“D”和电机参数的变化程度“m”所共同决定的。近似忽略所有的无穷小项，得到简化后的闭环系统特征方程表达式为

式中，a4=1；a3=–(1+a)；a2=2Dm+a–b；a1=b–(2a+1)Dm+bm；a0=aDm–bm。

于是，在保证系统稳定性的前提条件下，通过Juri 判据将能够分析得到本文预测无差拍控制算法的鲁棒性能，即不同预测权值“D”所能够适应的电机参数变化范围“m”，如图7a 所示。可以看到，图中所示的阴影区域界定了预测无差拍控制算法适应电机参数变化的稳定运行范围，其单调递减的曲线特性表明选取较小的预测权值“D”将使控制系统具有更出色的鲁棒性。

图7 基于预测无差拍控制的闭环特性分析Fig.7 Closed-loop characteristics of predictive dead-beat algorithm based control system

不过，由图7b 中所示系统的闭环特征根曲线图可知，过分优化的电机参数鲁棒性反而会降低系统的动态响应速度。伴随着预测权值“D”的增大，系统的特征根曲线将移向高带宽区域，此时系统的动态响应速度得到提高，但适应的电机参数变化也会随之减小。因此，预测无差拍控制参数的设计，需要同时兼顾系统的动态响应和适应电机参数变化的鲁棒性能。

事实上，在长期的运行过程中，电机参数的变化趋势通常无法预测。因此，本文建议：优化选取的预测权值“D”能够在±50%的电机参数变化范围内（即m=[0.5,1.5]），满足定子电流控制对动态响应和鲁棒性能的要求。于是，本文取D=0.3，并由此得到系统的闭环频率响应Bode 图，如图8 所示。

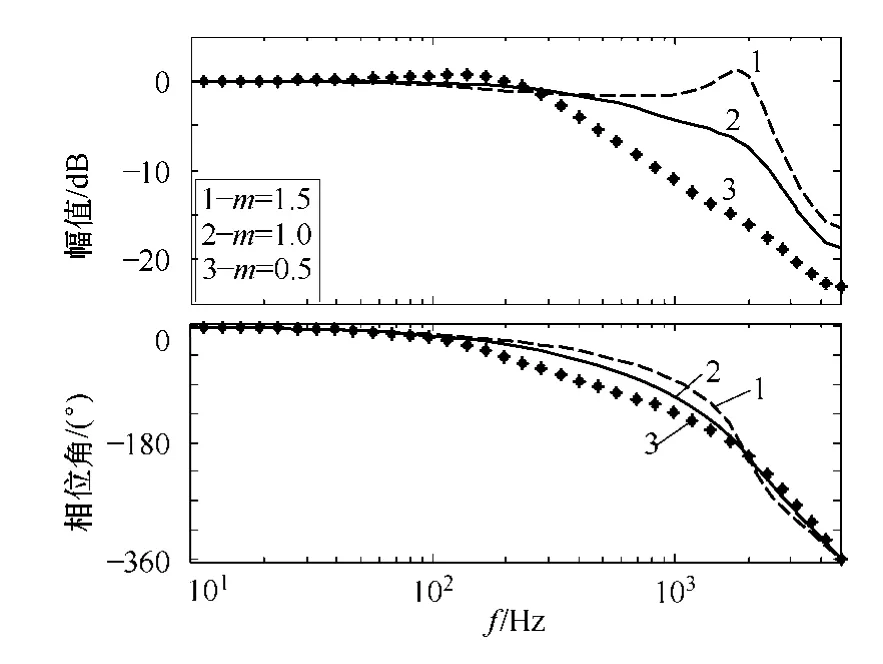
图8 不同电机参数条件下的闭环频率响应曲线Fig.8 Closed-loop frequency responses with vaired motor parameters

为了进一步实现PMSG的无传感器速度反馈调节，基于式（13）中串联补偿后的q 轴反电动势，可得到观测转速的离散状态表达式为

最后，在观测定向的d-q 参考坐标系下，采用预测无差拍电流控制，并基于式（18）实现电机的转速反馈，得到PMSG 完整的无传感器控制方案原理框图，如图9 中所示。

图9 完整的PMSG 无传感器控制原理框图Fig.9 Complete block diagram of the sensor-less control schecme for the PMSG

5 实验研究

5.1 试验系统说明

为了验证本文基于预测无差拍算法的无传感器控制方案，如图1 构建一套基于10kW PMSG的直驱发电试验系统，参数见下表。系统中采用独立调速的永磁同步电动机代替风力机，直接与PMSG 同轴相连，如图10 所示，而直流母线电压则由NSC建立并维持恒定，以使PMSG 能够由GSC 实施正常的发电控制。

表 试验系统的主要参数Tab. Main parameters of the experiment system

图10 原动机与发电机的试验模型Fig.10 Prototype of prime-motor and PMSG

控制单元以32 位浮点运算的TMS 320F 28335 DSP 为核心，并采集两相定子电流和电压分别实现控制与保护功能。PMSG 装载的11 位光电编码器，则作为本文无传感器观测算法的参考依据。在系统启动以前，接触开关K1隔离发电机组与并网变流器的连接，此时PMSG 由原动机带动，在50r/min的初始转速条件下空载运行。

5.2 基于预测无差拍的无传感器控制实验

在实验过程中，根据精确测量的电机参数（即m=1.0）和优化设计的控制器（D=0.3），实现如图9中所示的方案。考虑到原动机的转速由其调速装置独立调节的，无法完全模拟实际的风力机特性，但其足以验证本文对PMSG 所提出的无传感器控制。于是，首先在没有转速外环的条件下，通过人为设定PMSG的转速和转矩电流，得到PMSG 无传感器控制的动静态响应波形，如图11～图13 所示。

当电机空载运行在50r/min 时，闭合K1并以6A的转矩电流启动PMSG 进入发电状态。如图11 所示，SRF-PLL 在经过短暂的调节过程后，观测到的转子位置角θe迅速跟踪编码器输出的参考位置角θr，考虑编码器和D-A 芯片本身的精度，图中示出的观测误差角近似为零（Δθ≈0），满足对观测精度的要求。于此同时，A、B 两相定子电流几乎没有 超调地达到稳态，充分证明了本文预测无差拍控制出色的动态响应特性。随后，将转速和转矩电流分别提高至100r/min 和10A，如图12 所示，看到此时的观测位置角θe与其参考θr基本重合，而通过FFT 分析，A、B 相定子电流的THD 分别为1.23%和1.42%，具有较好的静态跟踪性能。图13 所示为估算反电动势在α-β 坐标系下的李萨如图，平滑的近似圆形间接验证了本文无传感器控制方案的出色性能。

图11 PMSG 无传感器控制的动态响应波形Fig.11 Dynamic performance of the sensor-less vector controlled PMSG

图12 PMSG 无传感器控制的静态响应波形Fig.12 Static performance of the sensor-less vector controlled PMSG

图13 估算反电动势在静止α-β坐标系下的李萨如图Fig.13 Lissajous figure of the estimated back EMF in stationary α-β frame

5.3 电机参数鲁棒性实验

在长期发电运行过程中，电机参数的变化不可避免、且无法预测，因而要求所采用的控制方案在一定范围内对参数变化具有鲁棒适应性。为此，本文采取主动改变电机模型参数的方式，包括交、直轴电感Ld和Lq,，以及电枢电阻Rs，使其发生±50%变化（即m=0.5 或1.5），以验证控制方案的鲁棒性。于是，当电机运行在100r/min，突然将转矩电流由6A 增大至10A，得到增大（m=0.5）和减小（m=1.5）电机模型参数时PMSG的动态响应过程，分别如图14a 和14b 所示。通过对比分析，除了θe与θr之间出现短暂的偏离过程，PMSG的无传感器控制性能几乎未受影响；而伴随转矩电流突减至6A，通过另一组鲁棒性实验波形，如图15a 和15b 所示，也可以得到同样的结论：即本文所提出的无传感器控制方案具有出色的鲁棒性能。

图14 改变电机模型参数的鲁棒性实验：PMSG 突增 发电功率的动态响应Fig.14 Robustness experiments with varied motor parameters:dynamic performances by suddenly increased power generation

图15 改变电机模型参数的鲁棒性实验：PMSG 突减 发电功率的动态响应Fig.15 Robustness experiments with varied motor parameters:dynamic performances by suddenly decreased power generation

随后，在增大预测权值（即D=0.5）的条件下，使控制模型中的电机参数发生相同程度的变化（即m从1.0 升至1.5），将导致PMSG的异常运行，包括畸变的定子电流、观测的转子位置角θe及其参考值θr，如图16 所示，这样充分验证了系统动态响应与鲁棒性之间需要协调设计、合理兼顾。

图16 改变预测权值系数“D”的鲁棒性实验：突增 电机模型参数“m”的动态响应波形Fig.16 Robustness experiments with predictive weight value “D”:dynamic performances by suddenly increased motor parameters “m”

5.4 观测转速的反馈调节实验

最后，加入观测转速反馈，进一步实现图9 中所示完整的无传感器控制方案，此时，原动机停止运行而仅作为大惯性环节，PMSG 则控制运行在电动状态。当人为设定转速指令由 30r/min 升高至150r/min 再回落至30r/min 时，得到PMSG 无传感器控制的动态响应波形，如图17 所示。由图17 可以看到，基于观测转速ωme的反馈调节能够快速、准确地实现速度指令跟踪；而转矩电流则在转速的突变过程中，总是会快速上升至限幅值，以便增大电磁转矩、加快转速跟踪的调节过程。而在完成速度跟踪后，PMSG 又将以很小的转矩电流来维持转矩的平衡和速度的恒定，这也间接地证明了此时转子位置角观测的准确性。

图17 无传感器控制PMSG的速度调节响应性能Fig.17 Speed regulation performance of the sensor-less controlled PMSG

6 总结

本文针对直驱风力发电系统中的永磁同步发电机提出了一套基于预测无差拍算法的无传感器控制方案，通过深入的理论分析和实验研究，可以得到以下结论：

（1）基于估算反电动势、采用同步锁相环的无传感器观测方法，能够快速、准确地获得转子的位置角和转速信息。

（2）预测无差拍控制算法使无传感器控制的PMSG 呈现出优异的动静态响应特性，并具有满意的电机参数鲁棒性能。

（3）最后，基于观测转速的速度反馈调节实验充分证明了本文所提控制方案在实际直驱式风力发电系统中的可行性。

[1]Chinchilla M,Arnaltes S,Burgos J C,et al.Control of permanent-magnet generators applied to variable speed wind-energy systems connected to the grid[J].IEEE Transactions on Energy Conversion,2006,21(1):130-135.

[2]赵仁德,王永军,张家胜.直驱式永磁同步风力发电系统最大功率追踪控制[J].中国电机工程学报,2009,29(27):106-111.Zhao Rende,Wang Yongjun,Zhang Jiasheng.Maximum power point tracking control of the wind energy generation system with direct-driven permanent synchronous generators[J].Proceedings of the CSEE,2009,29(27):106-111.

[3]Spooner E,Williams A C.Direct coupled permanent magnet generators for wind turbine applications[J].IEE Electronic Power Application，1996，143(1)：1-8．

[4]Li H,Chen Z.Overview of different wind generator systems and their comparisons[J].IET Renewable Power Generation,2008,2(2):123-128.

[5]Hansen A D,Michale G.Multi-pole permanent magnet synchronous generator wind turbines’ grid support capability in uninterrupted operation during grid faults[J].IET Renewable Power Generation,2009,3(3):333-348.

[6]Bianchi N,Bolognai S,Jang Ji Hong,et al.Comparison of PM motor structures and sensorless control techniques for zero-speed rotor position detection[J].IEEE Transactions on Industry Electronics,2007,22(6):2466-2475.

[7]齐放,邓智泉,仇志坚,等.一种永磁同步电机无速度传感器的矢量控制[J].电工技术学报,2007,22(10):30-35.Qi Fang,Deng Zhiquan,Qiu Zhijian,et al.A method of sensorless vector control of PMSM[J].Transactions of China Electrotechnical Society,2007,22(10):30-35.

[8]Qiao W,Yang X,Gong X.Wind speed and rotor position sensorless control for direct-drive PMG wind turbines[J].IEEE Transactions on Industry Electronics,2012,48(1):3-11.

[9]Kim H,Son J B,Lee J Y.A high-speed sliding-mode observer for the sensor-less speed control of PMSM[J].IEEE Transactions on Industry Electronics,2011,47(3):1337-1343.

[10]Prendl M,Schaltz E.Sensorless model predictive direct current control using novel second-order PLL observer for PMSM drive systems[J].IEEE Transactions on Industry Electronics,2011,58(9):4087-4095.

[11]年珩,李嘉文,万中奇.基于参数在线辨识的永磁风力发电机无位置传感器控制技术[J].中国电机工程学报,2012,32(12):146-154.Nian Heng,Li Jiawen,Wan Zhongqi.Sensor-less control technique of PMSG for wind power application based on on-line parameter identification[J].Proceedings of the CSEE,2012,32(12):146-154.

[12]王宏佳,杨明,牛里,等.永磁交流伺服系统电流环带宽扩展研究[J].中国电机工程学报,2010,30(12):56-62． Wang Hongjia,Yang Ming,Niu Li,et al.Current loop bandwidth extension for permanent magnet AC servo system[J].Proceedings of the CSEE,2010,30(12):56-62.

[13]Ho C N,Cheung V,Chung H S H.Constant-frequency hysteresis current control of grid-connected VSI without bandwidth control[J].IEEE Transactions on Power Electronics,2009,24(11):2484-2495.

[14]Kim K H,Youn M J.A simple and robust digital current control technique of a PM synchronous motor using time delay control approach[J].IEEE Transactions on Power Electronics,2001,16(1):72-82.

[15]Rodriguez J,Pontt J,Silva C A,et al.Predictive current control of a voltage source inverter[J].IEEE Transactions on Industrial Electronics,2007,54(1):495-503.

[16]Cortes P,Kazmierkowski M,Kennel R,et al.Predictive control in power electronics and drives[J].IEEE Transactions on Industrial Electronics,2008,55(12):4312-4324.

[17]Morel F,Shi X F Lin,Retif J M,et al.A comparative study of predictive current control schemes for a permanent magnet synchronous machine drive[J].IEEE Transactions on Industry Electronics,2009,56(7):2715-2728.

[18]Huerta J M E,Moreno J C,Fischer J R,et al.A synchronous reference frame robust predictive current control for three-phase grid-connected inverters[J].IEEE Transactions on Industry Electronics,57(3):956-962.

[19]Huerta J M E,Castello J,Gil R G,et al.An adaptive robust predictive current control for three-Phase grid-connected inverters[J].IEEE Transactions on Industry Electronics,58(8):3537-3546.

[20]陈荣.永磁同步电机的控制系统[M].北京:中国水利水电出版社,2009.