六相永磁容错磁通切换电机及其单相故障的容错控制

吴一丰 邓智泉 王 宇 王晓琳

（南京航空航天大学自动化学院 南京 210016）

1 引言

自1997年法国学者提出经典的12/10 永磁磁通切换（Flux Switching Permanent Magnet,FSPM）电机以来[1]，磁通切换电机吸引了国内外学者的广泛关注和研究[2-9]。FSPM 电机具有双极性正弦磁链，呈现出较强的聚磁效应，功率密度高，且永磁体无退磁风险，适用于交流无刷场合。针对目前各应用领域对电机调速系统可靠性要求的提高，目前国内外诸多学者致力于电机容错的研究[7-23]。容错电机系统不仅要求电机本体及功率变换器能够减小故障传染，抑制短路电流，同时须在故障状态下满足一定要求的转矩输出[10]。

目前，在容错电机本体方面，研究较为广泛的是转子永磁式容错电机[10-17,21-23]，而容错磁通切换电机本体的研究相对较为有限：文献[8]比较了磁通切换电机在不同的绕组绕制方法下的电磁性能，指出绕组隔齿绕制的磁通切换电机的自感更大，互感自感比更小，具备一定的容错潜质。文献[9]沿用转子永磁式容错电机的设计方法，在电机本体结构上获取了容错能力，但降低了电机的功率密度。

容错控制包含两方面：一是系统所采用的功率变换器结构，二是适用于特定变换器拓扑的容错控制策略。容错电机系统中采用较多的功率变换器拓扑有双功率变换器[9,12,18,19]、多相全桥变换器[13-15]、多相独立H 桥变换器等[10,16,17]。容错控制策略的目标是要保证电机在故障状态下仍能输出满足要求的转矩，现有的文献从磁动势不变或瞬时转矩不变的角度出发，其目标均是保证转矩的平滑。文献[13-15]根据故障前后旋转磁动势不变，得到容错补偿电流，但是均只考虑了开路缺相故障情况，未涉及短路故障容错。文献[16-20,22]的故障补偿策略均以瞬时转矩不变为出发点：最优转矩控制策略[16-17]结合拉格朗日乘数法等数学优化手段，达到转矩平滑输出且铜耗最小的目的，但是需要在线迭代计算；文献[19]针对绕组开路故障，将转矩分解为基波转矩和谐波转矩，在容错运行中施加补偿电流保证谐波转矩为零，从而保证瞬时转矩不变；最优电流控制策略[22]根据瞬时转矩不变得到瞬时电流幅值，在实现转矩无脉动输出的同时，保证铜耗最小。对于正弦波磁场电机，在不考虑空间谐波的情况下，根据磁动势不变得到的补偿电流仍为正弦，仅在相位和幅值上相应调整，而最优转矩控制、最优电流控制等方法的补偿电流中均含有大量谐波，增大了电机铁耗[23]。

本文在容错电机本体及控制策略两方面着手，研究了一种具备容错能力的六相永磁磁通切换电机，阐述分析了该电机的工作原理和电磁性能。基于磁动势守恒原则进行开路故障补偿，实现转矩脉动最小化的同时优化转矩铜耗比；针对短路故障提出一种故障分解补偿法，实现容错控制的同时避免了复杂的在线计算。样机的实验结果验证了该电机的高转矩密度和强容错能力，证明了所提容错控制策略的有效性。

2 电机结构和工作原理

图1 为本文研究的六相FTFSPM 电机结构，定子由六个单元组成，每一单元包含电枢绕组、永磁体和“E”形定子齿，“E”形的两个边齿的端部又分成两个齿。每个定子槽中只安放一个电枢绕组，实现绕组间的物理隔离和热隔离，以减小故障的传染。没有绕组的定子齿作为磁通回路，起到相与相之间磁隔离的作用，称之为隔磁齿。随着转子位置的变化，电枢绕组匝链的磁链呈双极性变化，电机工作原理如图2 所示。

图1 六相FTFSPM 电机截面示意图Fig.1 Profile configuration of 6-phase FTFSPM motor

图2 六相FTFSPM 电机工作原理Fig.2 Operational principle of 6-phase FTFSPM motor

在传统的12/10 FSPM 电机中，由于绕组的一致性和互补性，磁链呈双极性正弦变化。在六相FSPM 电机中，为解决绕组互补性缺失的问题，本文研究了轴向双层结构的拓扑。电机三维结构如图3所示，转子分成两部分，转子I 与转子II 相差机械角度1/2×(360°/p)≈9.5°，即电角度180°，其中p为转子极对数，在该电机中转子极对数为19。两部分定子结构相同，切向相同位置的两块永磁体充磁方向相反，两部分定子公用电枢绕组。以A 相绕组为例，定义位于定子I 中的部分为AI，位于定子II中的部分为AII，AI的磁路与AII的磁路相差半个周期，并且运动方向相反，即AI与AII存在互补性。图4 给出六相FTFSPM 电机在两部分定转子单独作用时的A 相磁链以及双层结构同时作用时的A、B、C 三相磁链。由图4 可见，轴向双层结构的设计解决了绕组互补性缺失的问题，提高了磁链正弦度。

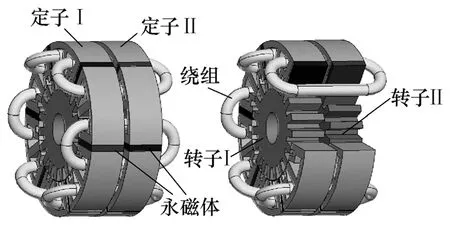
图3 六相FTFSPM 电机三维图Fig.3 3D model of the 6-phase FTFSPM motor

图4 FTFSPM 电机的相磁链Fig.4 Phase fluxes of FTFSPM motor

3 电磁性能分析

原理样机的主要参数见表1。

表1 优化FTFSPM 电机主要参数Tab.1 Major parameters of optimized FTFSPM motor

由有限元仿真得到的电机六相绕组的自感互感（只给出三相）及通过派克变换得到的交直轴电感如图5 所示，表2 给出了各项电感参数的平均值。可见电机的自感远大于互感，一相绕组与相邻相的互感约为该相自感的10%，非相邻相的互感约为零，可以忽略。较小的互感自感比说明了电机具有良好的磁隔离能力，故障影响小。交直轴电感基本保持恒定，两者在数值上相差甚微，该电机凸极效应不明显。图6 为用原动机拖动该电机，测得的a 相绕组短路前后的各相空载反电动势，与a 相相邻的b、f 相反电动势在a 相短路前后保持不变，验证了该电机具有较好的故障隔离能力。

图5 FTFSPM 电机电感特性Fig.5 Inductance characteristics of the FTFSPM motor

表2 FTFSPM 电机电感平均值Tab.2 Average inductance of FTFSPM motor

图6 空载反电动势Fig.6 Back-EMF at no load

FTFSPM 电机的转矩特性如图7 所示，定位力矩仅为额定平均转矩的2.6%。由于FTFSPM 电机定转子采用多齿结构，减小了磁路磁阻及磁阻变化率，在提高电机的出力的同时，减小了定位力矩，降低了转矩脉动。电流-转矩特性如图8 所示。

图7 FTFSPM 电机转矩特性Fig.7 Torque characteristics of the FTFSPM motor

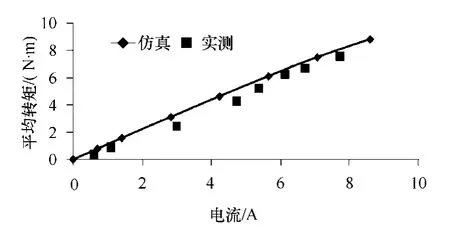
图8 FTFSPM 电机转矩-电流特性曲线Fig.8 Torque-current characteristic of FTFSPM motor

由于本文研究的电机为定、转子双凸极结构，而空间相对的两个线圈独立为一相，故障情况下存在不平衡磁拉力。本文讨论的是单相故障，在后续的研究中涉及了多相开路、短路以及两者的综合故障，在不对称多相故障中，不平衡磁拉力的影响更为显著。而磁拉力的研究涉及到电机径向力数学模型的理论推导分析[24-26]，出于篇幅的限制，本文中暂不涉及不平衡磁拉力的讨论。

4 开路故障控制

4.1 FTFSPM 电机的数学模型

由六相H 桥逆变器驱动的六相FTFSPM 电机如图9 所示，每相绕组由一个H 桥独立供电，以实现容错电机系统的电气隔离要求。

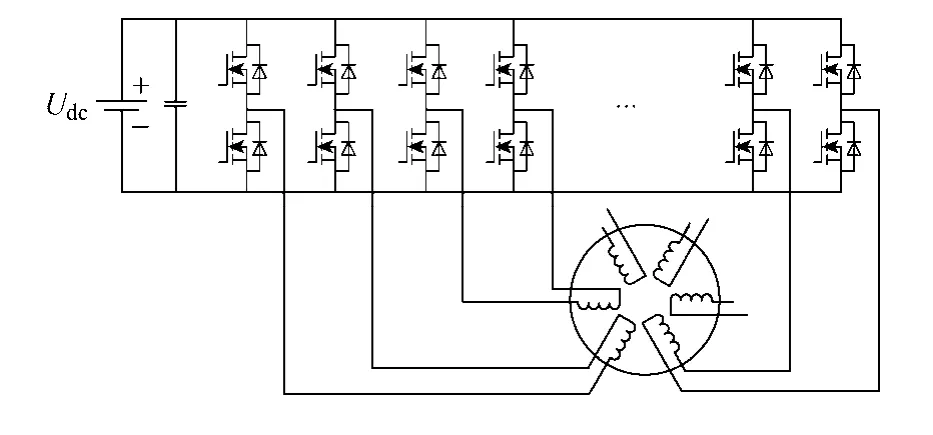
图9 六相H 桥和FTFSPM 电机Fig.9 six-phase H bridge and FTFSPM motor

在转子同步旋转坐标系中，稳态电压方程

式中ωe——电角速度，且ωe=pωr；

id1，iq1——直轴、交轴电流；

R——相绕组电阻；

ψm——永磁磁链幅值。

电磁转矩为

式中Pem——电磁功率。

系数3 是为了保证在自然坐标系下和dq 坐标系下功率守恒，因为本文中采用磁动势不变坐标变换，包含系数1/3。

4.2 开路补偿

由于FTFSPM 电机磁链呈双极性正弦变化，故一般采用正弦波控制方式。采用id1=0 控制，正常工作时电流为

式中Im——相电流幅值；

θ——转子电角度。

当某一相发生开路故障后，该相电流为零，缺失该相转矩，造成转矩脉动。此时需调节剩余五相的电流，补偿故障相缺失转矩，消除转矩脉动。

按照磁动势不变变换原则，从六相自然坐标系到正交坐标系的变换矩阵扩充为方阵

不失一般性，以a 相故障为例，下同。当a 相开路后，删除变换矩阵T6中与a 相相关的第1 列，剩余6 行中去除与第1 行不正交的3、5、6 行后，将剩余的三行扩充成正交方阵[14,15]

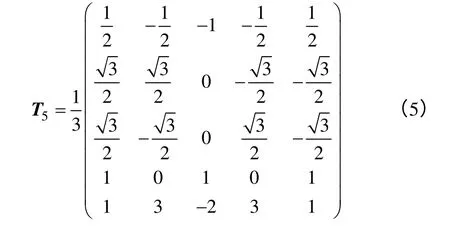
由于变换矩阵3～5 行对应的电流分量不能独立形成旋转磁场，因此相应的基波同步转速下变换矩阵3～5 行与转角θ无关，作为零序分量[15]，则选取旋转变换矩阵

自然坐标系下的电流变换成旋转正交坐标系下的电流

在id1=0 控制下，由式（2）可知，调节交轴电流iq1即可调节电磁转矩。在故障状态下，要输出与正常态下相同的转矩，则维持iq1不变。在各相绕组由H 桥逆变器独立供电的电机系统中，不存在零序电流为零的要求，但零序电流的大小会影响电机的铜耗。在上述所选的变换矩阵下，a 相开路后电机铜耗为

由式（8）可见，当满足

时，铜耗最小。结合id1=0，iq1保持不变，解方程（7）可得一组优化的补偿电流解

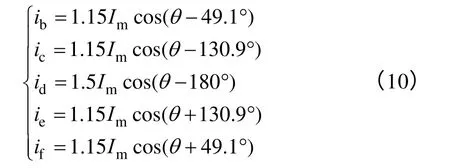
由式（10）可见，满足铜耗最小条件时，各相电流幅值不等。考虑到变换器功率的限制，用各相铜耗相等条件（11）替代铜耗最小条件（9）

式中，Ib～If分别表示b～f 相的电流幅值。

可解得一组补偿电流为

各相电流幅值相等，均为六相正常工作时电流幅值的1.236 倍。

5 短路故障控制

5.1 短路补偿策略

与开路故障相比，短路故障不仅存在由于缺相造成的转矩缺失与转矩脉动，还存在短路电流引起的转矩脉动。针对短路故障，本文提出一种故障分解补偿策略，补偿电流仍为正弦；在测得短路电流的情况下，无需复杂的在线计算，不额外增加数字控制器的负担。

某一相短路可分解为两种故障的合成：故障一由该相短路电流引起，故障二由该相正常电流缺失引起，可认为由该相开路引起。因此故障补偿分解为两步：一是用非故障相补偿故障相短路电流，消除短路电流造成的脉动磁动势，使得合成磁动势为零，即消除短路电流引起的转矩脉动；二是补偿故障相开路，直接采用开路故障的补偿策略，无需重复计算。将两部分的优化补偿电流矢量合成，即可得到短路故障的优化电流。

不失一般性，以a 相短路为例，短路电流为

式中Ik——短路电流幅值。

忽略绕组电阻的影响，短路电流幅值为常值，不随转速变化

由有限元仿真得到的磁链幅值和自感值计算得到短路电流Ik=6.3A。设补偿a 相短路电流的非故障相电流为ibI，icI，idI，ieI，ifI，则合成磁动势为

式中N——一相绕组匝数；

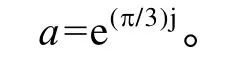
令合成磁动势MMFI=0，得

若不加约束条件，补偿电流有无穷多组解。为利用Matlab 数值求解工具，设

设置表征绕组铜耗的目标函数为

将式（17）代入式（16）可得方程组

以函数f取得最小值为目标，利用Matlab 数值优化工具可得一组最优解

因此优化的补偿电流为

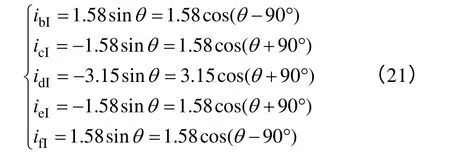
对非故障相b～f 施加上述电流后，与a 相短路电流合成磁动势为零，因此此时可视为a 相绕组开路，应对开路故障进行补偿。

第二部分，作为a 相开路故障进行补偿，采用第3.2 节中得到满足最大转矩铜耗比或铜耗相等的补偿电流，即可补偿缺相转矩及脉动转矩。两部分补偿电流矢量合成，得到合成补偿电流为

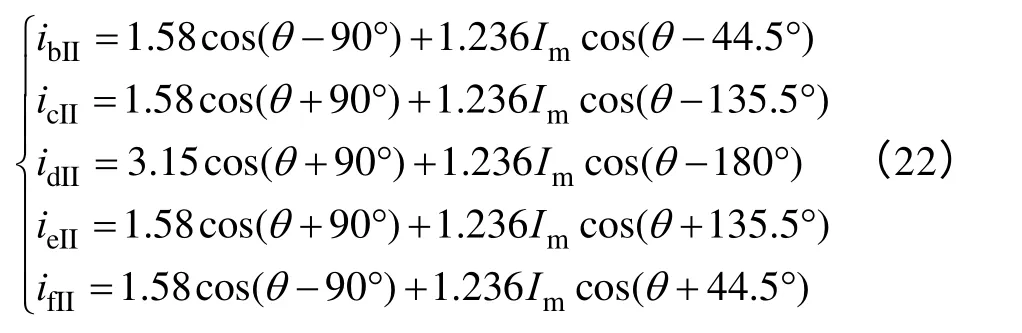
5.2 不同短路补偿策略的比较

故障分解法在两步补偿中均实现了铜耗最小，最后补偿电流矢量合成。为探究该补偿策略合成铜耗的大小，本小节对故障分解补偿法和最优电流控制策略[22]的铜耗进行了比较，以最优电流法的铜耗为基值，结果见表3。表中故障分解法1 表示补偿开路故障部分采用铜耗相等原则，故障分解法2 表示补偿开路故障部分采用铜耗最小原则。可见，一方面，不同补偿策略的铜耗相差甚微，另一方面，随着负载的增大，故障分解补偿策略铜耗增加的速度小于最优电流控制策略。

表3 不同补偿策略铜耗Tab.3 Copper loss of different compensation strategies

6 实验验证

原理样机实物如图10 所示，给出了定转子叠片结构、电机整体及加载试验图，电机负载由加载器控制给定。系统控制框图如图11 所示，采用矢量控制，转速环PI 得到交轴电流幅值，结合id1=0，通过旋转坐标到自然坐标系的变换得到相电流给定值；采样得到相电流值与给定值PI 得到H 桥开关管状态。功率变换器相电流最大值限制为9A。

图10 FTFSPM 电机样机及加载试验系统Fig.10 Prototype of FTFSPM motor and load experiment setup

图11 FTFSPM 电机系统id1=0 矢量控制框图Fig.11 Diagram of id1=0 vector control of FTFSPM motor

6.1 正常工作

电机六相正常工作时，各相电流按式（3）给定，在转速400r/min，70%额定负载情况下的实验结果如图12 所示，转速和电流均能较好地跟踪给定。

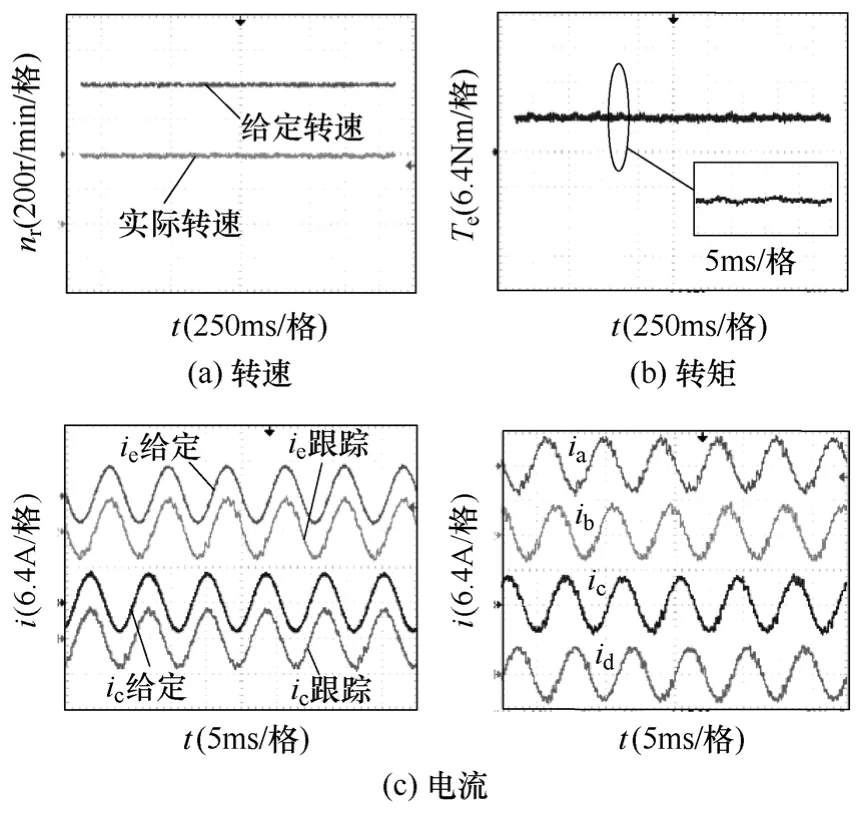
图12 六相正常工作Fig.12 Healthy work

6.2 单相开路故障试验

根据控制框图可知，开路故障后若不进行补偿，由于平均转矩的缺失使得转矩不平衡，此时转速PI自动调节输出，给定电流1增大，维持输出转矩的平均值不变，但是无法对转矩脉动进行补偿。图13和图14 分别为a 相开路故障不补偿转矩脉动和补偿后的转速、转矩和相电流。考虑到功率变换器电流的限制，采用铜耗相等原则，补偿电流各相幅值相等。比较图12c 和图14c，相电流幅值为六相正常工作时的1.3 倍，与3.2 节理论计算值基本相符。比较图13b 和图14b，补偿后脉动减小，验证了补偿策略的有效性。

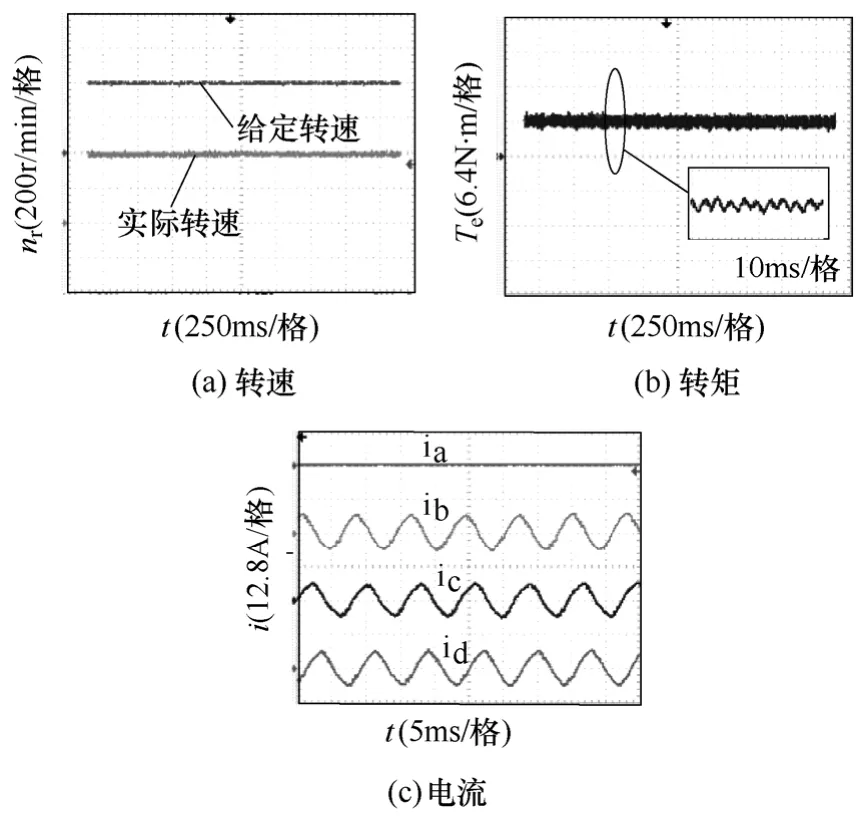
图13 a 相开路不补偿Fig.13 Phase a open-circuit fault without compensation

图14 a 相开路补偿Fig.14 Phase a open-circuit fault with compensation

6.3 单相短路故障试验

考虑到功率变换器对相电流幅值的限制，在短路故障中降额使用，转速保持400r/min，输出转矩5N·m。采用4.1 节中故障分解法对a 相短路故障进行补偿，补偿前后转速、转矩和相电流分别如图15和图16 所示。比较图15b 和图16b，补偿后的转矩脉动减小。

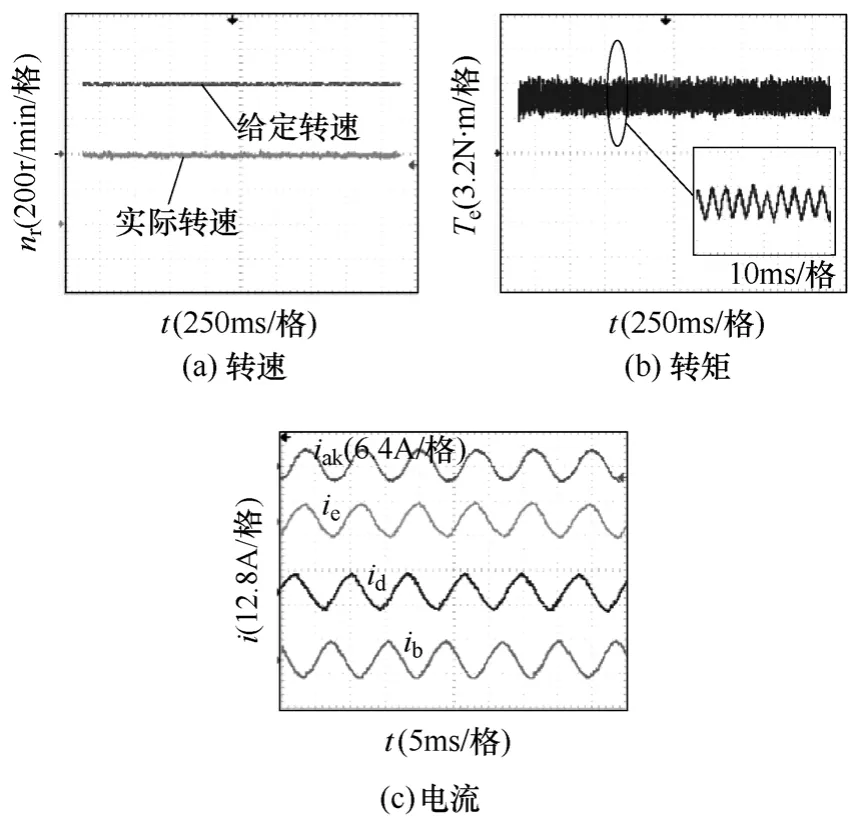
图15 a 相短路不补偿Fig.15 Phase a short-circuit fault without compensation

图16 a 相短路补偿Fig.16 Phase a short-circuit fault with compensation

7 结论

本文研究了一种新型的六相永磁容错磁通切换电机，有限元仿真和实验验证了该电机具备强容错能力。研究了单相开路故障和短路故障的补偿策略，实验验证了补偿策略的有效性。具体结论如下：

（1）FTFSPM 电机继承了永磁磁通切换电机的结构特点和功率密度优势，磁链双极性变化，正弦度高。多齿结构在提高电机的出力的同时，减小了定位力矩，降低了转矩脉动。绕组自感大，互感自感比小，具备故障隔离和抑制短路电流的能力。

（2）针对电机开路故障，通过坐标变换，在同步旋转坐标系下扩充零序分量，通过对零序分量的控制解析得到优化的补偿电流。

（3）针对短路故障，提出短路故障可分解为两种故障的合成，进一步提出故障分解补偿策略。首先根据磁动势相等原则，利用非故障相补偿故障相短路电流，消除短路电流引起的转矩脉动；其次直接采用开路故障的补偿策略补偿开路转矩脉动。在每一步中均优化设计达到最大转矩铜耗比或最大转矩输出的要求。

（4）在测得短路电流的前提下，故障分解补偿法无需复杂的在线计算，降低了对数字控制器要求。矢量合成的补偿电流不含高次谐波，提高了电机的容错运行性能。

[1]Hoang E,Ben Ahmed A H,Lucidarme J.Switching flux permanent magnet polyphased synchronous machines[C].The 7th European Conference on Power Electronic and Applications,1997:3903-3908.

[2]Zhu Z Q,Pang Y,Iwasaki S.Analysis of electromagnetic performance of flux-switching permanent-magnet machines by nonlinear adaptive lumped parameter magnetic circuit model[J].IEEE Transactions on Magneties,2005,41(11):4277-4287.

[3]Hua W,Cheng M,Zhu Z Q,et al.Analysis and optimization of back EMF waveform of a flux-switching permanent magnet motor[J].IEEE Transactions on Energy Conversion,2008,23(3):727-733.

[4]Zhu Z Q,Chen J T,Pang Y,et al.Analysis of a novel multi-tooth flux-switching PM brushless AC machine for high torque direct-drive applications[J].IEEE Transactions on Magnetics,2008,44(11):4313-4316.

[5]Chen J T,Zhu Z Q.Winding configurations and optimal stator and rotor pole combination of flux-switching PM brushless AC machines[J].IEEE Transactions on Energy Conversion,2010,25(2):293-302.

[6]Zhu Z Q.Recent advances on permanent magnet machines[J].Transitions of China Electrotechnical Society,2012,27(3):1-11.

[7]Chen J T,Zhu Z Q,Iwasaki S,et al.A novel e-core flux-switching PM brushless AC machine[C].Energy Conversion Congress and Exposition,2010:3811-3818.

[8]Chen J T,Zhu Z Q.Comparison of all and alternate poles wound flux-switching PM machines having different stator and rotor pole numbers[J].IEEE Transitions on Industry Applications,2010,46(4):1406-1415.

[9]Raminosoa T,Gerada C.Novel fault tolerant design of flux switching machines[C].Power Electronics,Machines and Drives(PEMD 2010),2010:1-6.

[10]Mecrow B C,Jack A G,Haylock J A,et al.Fault-tolerant permanent magnet machine drives[J].IEE Proceedings Electric Power Applications,1996,143(6):437-442.

[11]赵文祥,程明,朱孝勇,等.驱动用微特电机及其控制系统的可靠性技术研究综述[J].电工技术学报,2007,22(4):38-46.Zhao Wenxiang,Cheng Ming,Zhu Xiaoyong,et al.An overview of reliability of drive system for small and special electric machines[J].Transactions of China Electrotechnical Society,2007,22(4):38-46.

[12]杨金波,李铁才,杨贵杰.一相开路双三相永磁同步电机建模与控制[J].电工技术学报,2011,26(10):167-173.Yang Jinbo,Li Tiecai,Yang Guijie.Modeling and control of dual three-phase PMSM with one open phase[J].Transitions of China Electrotechnical Society,2011,26(10):167-173.

[13]Fu Jen Ren,Thomas Lipo A.Disturbance-free operation of a multiphase current-regulated motor with an opened phase[J].IEEE Transitions on Industry Applications,1994,30(5):1267-1274.

[14]Hyung Min Ryu,Ji Woong Kim,Seung Ki Sul.Synchronous-frame current control of multiphase synchronous motor under asymmetric fault condition due to open phases[J].IEEE Transitions on Industry Applications,2006,42(4):1062-1070.

[15]赵品志,杨贵杰,李勇.五相永磁同步电动机单相开路故障的容错控制策略[J].中国电机工程学报,2011,31(24):68-76.Zhao Pinzhi,Yang Guijie,Li Yong.Fault-tolerant control strategy for five-phase permanent magnetic synchronous motor under single phase open-circuit fault condition[J].Proceedings of the CSEE,2011,31(24):68-76.

[16]Jiabin Wang,Kais Atallah,David Howe.Optimal torque control of fault-tolerant permanent magnet brushless machines[J].IEEE Transactions on Magnetics,2003,39(5):2962-2964.

[17]Sun Zhigang,Wang Jiabin,Jewell Geraint W,et al.Enhanced optimal torque control of fault-tolerant PM machine under flux weakening operation[J].IEEE Transactions on Industrial Electronics,2010,57(1):344-353.

[18]Zhao Wenxiang,Cheng Ming,Chau K T,et al.Stator-flux-oriented fault-tolerant control of flux-switching permanent-magnet motors[J].IEEE Transactions on Magnetics,2011,47(10):4191-4194.

[19]Zhao Wenxiang,Cheng Ming,Hua Wei,et al.Back-EMF harmonic analysis and fault-tolerant control of flux-switching permanent-magnet machine with redundancy[J].IEEE Transactions on Industrial Electronics,2011,58(5):1926-1935.

[20]Zhao Wenxiang,Cheng Ming,Hua Wei,et al.Post-fault operation of redundant flux switching permanent magnet motors using harmonic injected current[C].International Conference on Electrical Machines and Systems,2010:868-872.

[21]郝振洋,胡育文,黄文新,等.转子磁钢离心式六相十极永磁容错电机及控制策略[J].中国电机工程学报,2010,30(30):81-86.Hao Zhenyang,Hu Yuwen,Huang Wenxin,et al.Six-phase ten-pole fault tolerant permanent magnet machine and its control strategy[J].Proceedings of the CSEE,2010,30(30):81-86.

[22]郝振洋,胡育文,黄文新,等.永磁容错电机最优电流直接控制策略[J].中国电机工程学报,2011,31(6):46-51.Hao Zhenyang,Hu Yuwen,Huang Wenxin,et al.Optimal current direct control strategy for fault tolerant permanent magnet motor[J].Proceedings of the CSEE,2011,31(6):46-51.

[23]Jason D Ede,Kais Atallah,Jiabin Wang,et al.Effect of optimal torque control on rotor loss of fault-tolerant permanent-magnet brushless machines[J].IEEE Transactions on Magnetics,2002,38(5):3291-3293.

[24]邓智泉,杨钢,张媛,等.一种新型的无轴承开关 磁阻电机数学模型[J].中国电机工程学报,2005,25(9):139-146.Deng Zhiquan,Yang Gang,Zhang Yuan,et al.An innovative mathematical model for a bearingless switched reluctance motor[J].Proceedings of the CSEE,2011,25(9):139-146.

[25]曹鑫,邓智泉,杨钢,等.无轴承开关磁阻电机麦克斯韦应力法数学模型[J].中国电机工程学报,2009,29(3):78-83.Cao Xin,Deng Zhiquan,Yang Gang,et al.Mathe-matical model of bearingless switched reluctance motors based on maxwell stress tensor method[J].Proceedings of the CSEE,2009,29(3):78-83.

[26]王晓琳,任新宇,邓智泉,等.短路容错控制在多相无轴承永磁同步电机中的可行性分析[J].电工技术学报,2012,27(3):105-118.Wang Xiaolin,Ren Xinyu,Deng Zhiquan,et al.Feasibility of fault-tolerant control of multi-phase permanent magnetic bearingless motors with short-circuited phases[J].Transactions of China Electrotechnical Society,2012,27(3):105-118.