基于旋转柔度的汽车发电机安装系统对其噪声的影响分析

鲍晓华 刘谋志 吴 锋 李佳庆

（合肥工业大学电气与自动化工程学院 合肥 230009）

1 引言

爪极汽车发电机电磁噪声产生机理及噪声辐射已成为广泛关注并研究的课题。研究电磁噪声产生机理及辐射机理，目的是为了在电机运行时减少电机的辐射噪声。目前常用的研究方法是：通过集总参数和等效电路的建模仿真[1,2]，以及相关实验技术，对电机运行时的电磁噪声源进行研究。通过抑制产生电磁噪声的电磁力以及改进电机定/转子的刚性，来达到低电磁噪声汽车发电机的要求。在这种研究方法中，往往假设爪极发电机的一个主要噪声辐射机制是定子铁心的动态响应、电机外壳、旋转转子和定子之间的脉动电磁力相互作用，并重点考虑了通过降低转矩脉动来达到降低电磁噪声的目的[3]。这也是传统电磁噪声理论在爪极发电机中的一个典型应用，显然没有考虑汽车发电机转子旋转及其安装结构安装脚灵活性等导致的动态效果。

事实上，根据爪极发电机使用情况来看，除了依照径向力的外壳动态响应，所存在的安装结构对噪声辐射的影响是很显著的。电磁噪声源、转矩脉动和安装结构相关性极高，一个给定的爪极发电机的辐射噪声随着装配参数的变化而改变。在对电机系统或是机械系统的柔度耦合和噪声分析计算中，国内外相关文献都取得了相应的成果。文献[4]中应用统计能量法，对电机的噪声产生和传播路径从机理层面进行了剖析，将电机的各个部分划分为各个能量产生和传播系统，并将它们进行耦合，实现了电机中运用统计能量法进行噪声分析。文献[5]对汽车发电机的噪声产生机理进行了比较详尽的分析，特别是从电机结构系统方面运用能量流动的基本概念，对汽车发电机各个部件进行了能量耦合的噪声分析，文中以四个安装脚结构系统为例进行了理论分析。文献[6,7]分别运用统计能量法对系统不同部件的能量流动进行耦合分析，并基于统计能量分析提出通用的、简单的模型预测声学性能，考虑了复杂的安装结构配置。文献[8,9]分别对定、转子组成的系统的磨合应用旋转柔度进行了耦合，并应用柔度的概念对滚动轴承转子的动态平衡进行分析。文献[10,11]运用耦合的基本原理和建模分析方法，建立了非参数模型并实现了智能优化算法在汽车发电机性能优化中的运用。迄今为止，还缺乏专门针对汽车发电机安装系统对其噪声的影响分析的文献报道。

综合爪极发电机电磁噪声源、转矩脉动和安装结构，优化爪极汽车发电机的低辐射噪声安装结构设计方法是一个亟待解决的问题。本文着重介绍了考虑安装结构对噪声辐射声功率影响的爪极汽车发电机噪声分析方法。为了建模的需要，引入旋转柔度将电机机壳与安装结构解耦。将每个安装结构简化为只有平动和与电机同旋转方向的两个自由度。设计变量取每个安装结构相对于转轴中心线的位置和每个安装结构接口处的刚度。将电机本体与安装结构统一起来建立一个低阶模型，以降低汽车发电机安装结构整体噪声为基本目标，实现其安装结构的优化配置。

2 汽车发电机安装结构旋转柔度模型的建立

汽车交流发电机的固定方式，常采用单挂脚、双挂脚以及无挂脚（抱持式），即安装脚多采用两到三个，而国外则有四个安装脚及以上。现工程实际应用中，汽车发电机常常采用三个安装脚将其固定于发动机上，其中两个脚位于一侧而第三个脚位于另一侧，且三个安装脚组成的平面与汽车发电机轴线平行。本文研究的典型汽车发电机安装结构如图1 所示。

图1 汽车发电机典型安装结构Fig.1 Typical structure of the alternator

将发电机安装系统进行耦合与模型简化，示意图如图2 所示。图中1 为电机安装结构整体（图中只画出一个安装脚），2 为带三个安装脚的电机系统耦合的示意模型。

图2 有三个安装脚时发电机的一个安装结构的耦合状况Fig.2 The installation structure coupling situation of the alternator with three installation feet

为引入旋转柔度将电机机壳与安装结构解耦，将每个安装结构简化为只有平动和与电机同旋转方向的两个自由度，则每个安装脚的挠曲决定于三个 位 移矢量和三 个 旋转矢量，即DT=[x,y,z,ψ,θ,φ]。假设存在一个很小的位移和旋转，此成分由以下两点构成：源于转轴系统的三个位移参数xs，ys，zs；以及关于转轴z，y，x的三个刚性外壳旋转参数ψs，θs，φs。如图2 所示。典型安装脚的位移和旋转由定义。

势能由电机和安装脚之间相对位移决定的个体刚度元素势能合成。与典型安装脚处的电机/安装结构接口有关的势能是

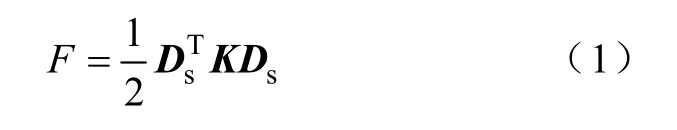
式中

图2 展示了安装在其基础上的作为悬臂梁的安装结构的理想化模型。对于拥有三个安装脚的安装结构的独立运动，应该有18 个约束角自由度，假设每个安装脚有三个平移度和三个旋转度。

引入安装结构质量和刚度矩阵M和K。安装脚处的偏移和旋转由在典型安装脚处的位移矢量定义，显然这符合机械模型的耦 合安装结构模型的直接组装过程。

总结上述问题，18 个角自由度与约束角自由度相关。约束角自由度的数量取决于固定约束自然频率与驱动频率的期待范围相比较的结果。在之后的计算表述中，安装结构被简化为一个梁。则可得组装电机系统振动方程为[12]

式中M，G，K——质量、阻尼和刚度矩阵；

q——广义位移矢量；

Q0——广义力谐波矢量的振幅；

N0——转矩脉动对应谐波次数；

Ω——转子旋转角速度。

统计能量分析法利用统计模态的概念[13]，一般用来分析并预测电机的中高频振动。根据爪极电机的使用工况，这里采用在中高频段预测电机噪声的统计能量分析法，是为了将机壳和安装结构解耦的需要。

将式（2）进行模式分解，特征向量以相应的特征值升序的顺序被排列为模型矩阵Φ。随着变换坐标q=Φ p。

以及

所获得的低阶解耦模型为

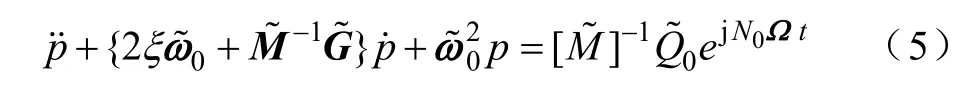
式中ξ——临界阻尼。

3 汽车发电机机械结构对其电磁噪声辐射的影响机制

由于电机磁场相互作用产生的电磁力作用在定子和转子之间的气隙中，其力波在气隙中是旋转的且是脉动的，力的大小与电磁负荷、电机有效部分的某些结构和计算参数有关。因此在设计任务中通常需要优化电机的计算和结构参数，以保证最大程度的削弱电磁激振力和传给电机机座的振动。

在常规的12 极36 槽汽车用爪极发电机中，气隙磁场谐波主要产生6 次及其整数倍次谐波的径向力作用在定转子上，产生转矩波动，进而引起发电机的电磁噪声。由空间某点作用的单位面积上径向激振力瞬时值为

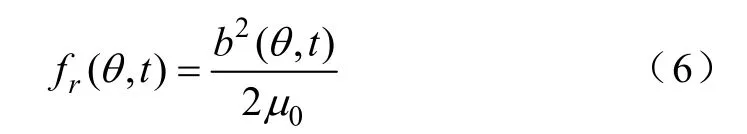
式中 b(θ,t)——气隙中距坐标轴线圆周角θ的某 一点在时间t的气隙磁密瞬时值；

μ0——空气磁导率。

针对额定功率1 000W，额定转速6 000r/min的汽车发电机气隙磁场及其径向电磁力的各次谐波仿真结果如图3 所示。

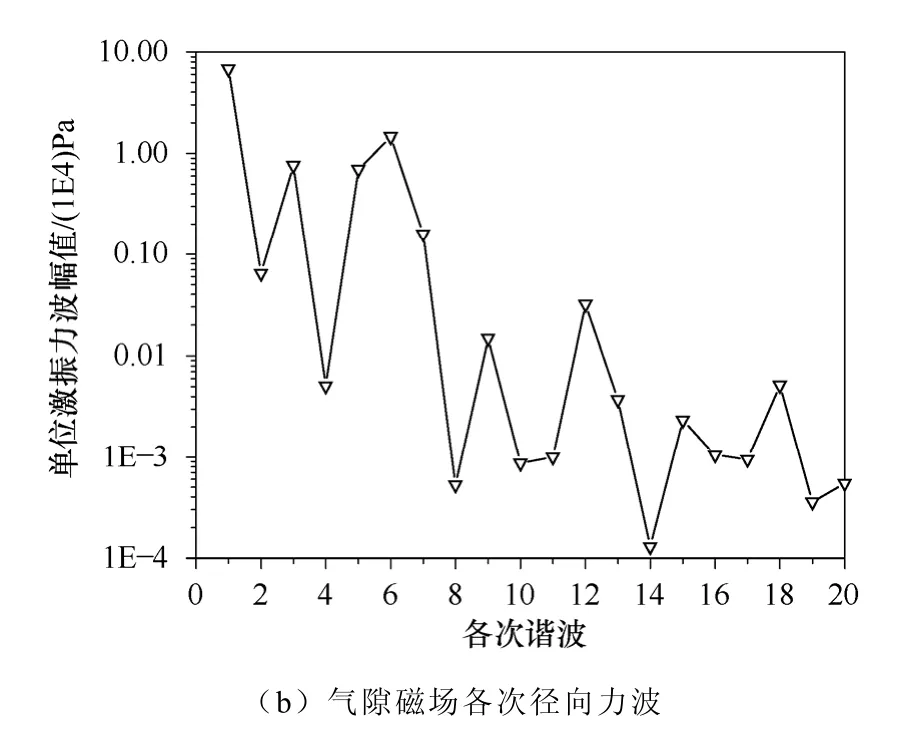
图3 发电机气隙磁场及其径向电磁力各次谐波Fig.3 The harmonic of air gap magnetic field and the radial electromagnetic force of the generator

由噪声辐射能量的路径，气隙磁场中的径向电磁力产生的振动能量首先引起定子轭的径向振动。在汽车发电机中，定子铁心主要是刚性固定在机壳内，这时电机振动声响特性在很大程度上和机壳的性质有关。因此，当计算振动时，除定子铁心的机械阻抗zc外，必须考虑机壳的阻抗

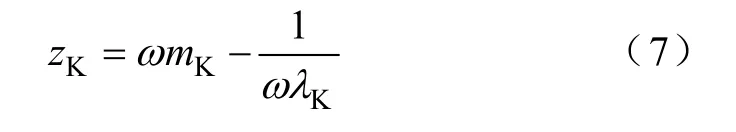
式中ω——激振力的频率；

mK——机壳的振动质量；

λK——机壳的柔度。

这时机壳表面的振动速度为

式中p0——定子轭平均圆周的单位激振力幅值。

由于铁心刚性支撑在机壳内，机壳和铁心的空间振动形式是一样的。此时发电机整体的噪声辐射特性与其外部安装结构的安装脚灵活性等导致的动态效果密切相关，即一个给定的汽车发电机的辐射噪声随着装配参数的变化而改变。存在一个与响应转矩脉动的安装结构有关的噪声辐射机制，安装结构对电机噪声的反应，是电机响应电磁转矩脉动造成的。利用机器轴和没有净力的耦合，一个理想的安装结构会响应机器外壳的旋转。

4 基于旋转柔度的汽车发电机安装结构的优化配置

实验观察到的安装结构中的位置加速度在机轴前/后方向、或者在侧向和横向都存在。汽车发电机的很多安装结构中，前向和后向、侧向和横向的安装结构为噪声响应提供有效的声辐射表面，此外，净力通过安装结构传输到发动机缸体可以有效地把机器和大声辐射结构耦合[14]。

所研究的汽车发电机组装系统有三个安装脚，每个安装脚相当于由线性弹簧以及相应的旋转弹簧从三个正交方向加以约束，如图4 所示。文献[15]提出关于安装脚的刚度对称性假设，电机质量和几何参数大致是固定的。选取参考轴系统的原点在电机安装系统的质心位置点B。要变化的几何参数是安装脚平面上轴的垂直坐标（z1）以及三角形安装脚的质心坐标，相对于参考轴系统原点的参考坐标为（xcm，ycm，zcm）。轴和外壳的质心是一致的。Zcm被认为是0，抵消垂直质量的作用完全是由于z1。

图4 汽车发电机安装结构耦合示意图Fig.4 The installation structure coupling schematic diagram of the alternator

图4 所示为汽车发电机安装结构简化图，其中a，b，c 三点所示为电机系统外部结构上的三个脚，且A 点为三个安装脚构成几何的质心；abc 平面平行于某一穿过电机轴线的平面OO’Q’Q。其中点B为电机系统质心。同时也为所选参考轴系统的原点坐标，即B 点坐标为（x=0,y=0,z=0）。

可得最佳的配置为把三角形安装脚的中心（xcm，ycm，z1）安置在参考质心点B的垂直线上。也就是说，当电机系统的质心和安装脚的质心位于同一垂直线上时，即当（xcm=0，ycm=0，z1）时，将达到“最佳”的配置。此配置的模拟显示，即使这个配置与不对称轴轴承刚度耦合，也没有净力从任何方向传递到连接结构，即发动机上。每个脚上有垂直的力，其实际结果是对电机旋转的耦合反应。

因此，在充分利用发电机安装系统的旋转柔度耦合的作用时，需要针对电机安装系统的质心调整与校正其安装脚的质心，直到两质心位于同一垂直线上。由图4 所示，即调整安装脚abc 平面，使其质心A 与电机系统质心B 点位于同一垂直线上为止，此时电机安装系统在旋转柔度的耦合作用下，电机系统对本身噪声的消减达到一个最佳状态。

5 噪声实验及其结果对比分析

为了试验验证汽车发电机安装结构旋转柔度对其噪声性能的影响，本文在噪声实验室针对实际使用中常规配置安装发电机（额定功率1 000W 级）进行相关噪声性能的测试，发电机完全采用实际安装发动机上的方式进行安装。得出噪声性能测试结果如图5a 所示。之后应用文中的旋转柔度耦合模型基本原理对同种型号的发电机优化配置安装结构，即改变三个安装脚组成平面位置，使发电机安装系统质心点B 与安装脚质心点A 位于同一垂直线上，然后在完全相同的实验条件下对其相关噪声性能进行测试，并得出相应噪声性能结果如图5b 所示。

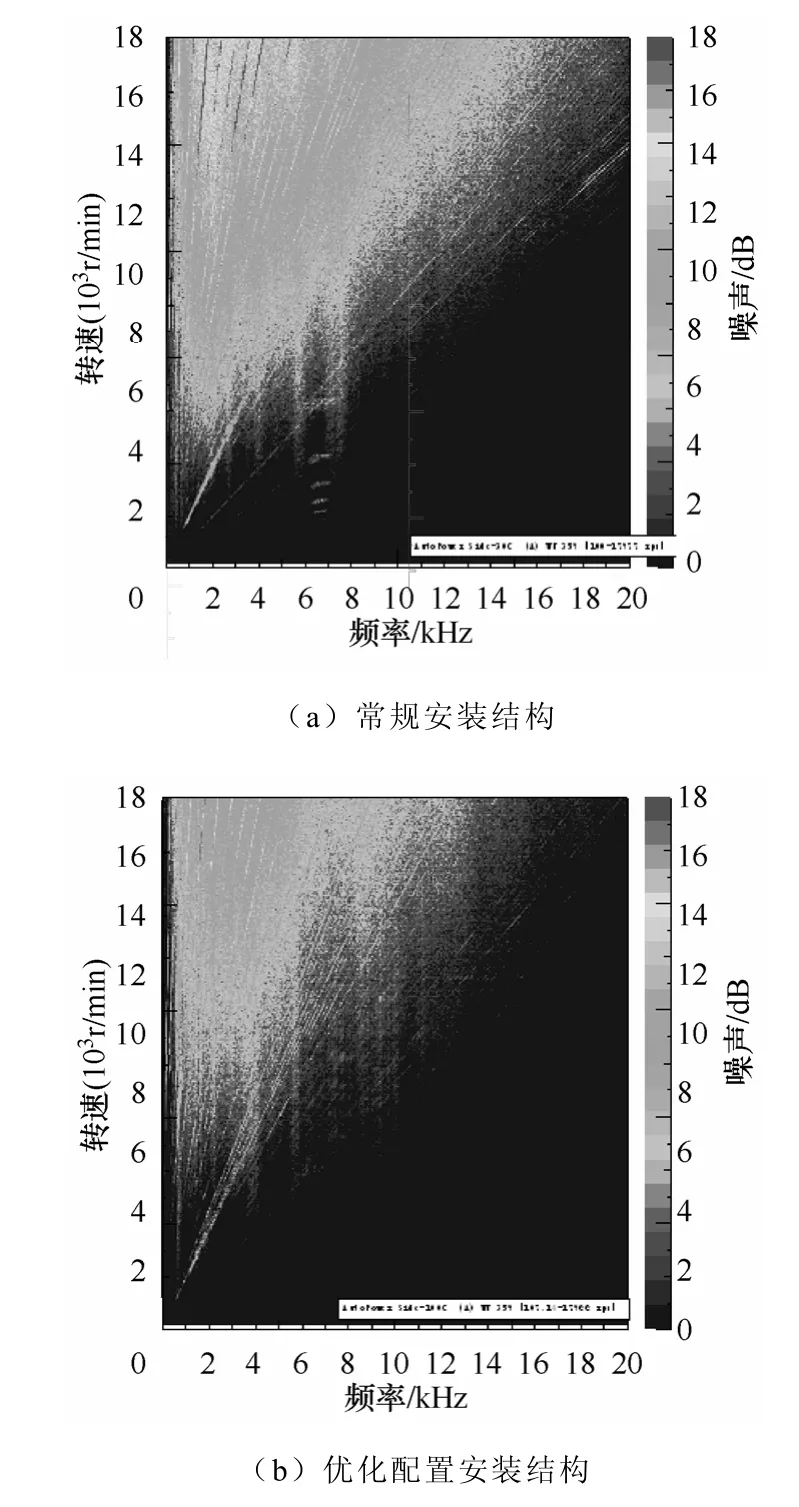
图5 实验测得同一型号汽车发电机优化配置 安装结构前后的相关噪声性能Fig.5 The experiment results of the noise performance of the same type alternator before and after optimal allocation installation structure

图5 所示为随着电机转速曲线的变化、不同频率阶次噪声的声级实验测量值，其中常规安装结构发电机噪声性能的测试转速为100～17 977r/min，各阶次噪声频率为0～20 000Hz，相应声级等级为40～90dB；优化配置安装结构发电机噪声性能的测试转速为107.14～17 966r/min，各阶次噪声频率为0～20 000Hz，相应声级等级为40～90dB。比较汽车发电机优化配置安装结构前后的噪声性能测试结果显然可见，优化配置安装结构后所得样机噪声性能测试结果有明显改善。且优化配置安装结构后所得样机噪声性能测试结果表明，在高转速，特别是汽车发电机额定转速6 000r/min 附近及以上时，高频率阶次噪声的声级减小明显。

6 结论

本文研究了不同安装结构情况下，爪极电机电磁噪声的变化模型，并为准确获得旋转柔度计算模型做试验验证。进行了气隙磁导不变情况下爪极电机加工装调结合不同的旋转柔度试验，探索了爪极电机电磁噪声控制技术。由实验结果验证可知，运用安装结构旋转柔度的模型优化汽车发电机的安装结构可有效改善电机本身以及与之相连的结构的振动和噪声情况。

致谢 本文中的实验测试数据是在万得集团锦州汉拿电机有限公司的噪声实验室测得，在其研究院工作人员的大力支持下完成，在此向他（她）们表示衷心的感谢。

[1]Sang Ho Lee,Soon O Kwon,Jeong Jong Lee,et al.Characteristic analysis of claw-Pole machine using improved equivalent magnetic circuit[J].IEEE Transactions on Magnetics,2009,45(10):4570-4573.

[2]Ibala A,Masmoudi A.Accounting for the armature magnetic reaction and saturation effects in the reluctance model of a new concept of claw-pole alternator[J].IEEE Transactions on Magnetics,2010,46(11):3955-3961.

[3]Reinap A,Hagstedt D,Hogmark C,et al.Sub-optimization of a claw-pole structure according to material properties of soft magnetic materials[J].IEEE Transactions on Magnetics,2012,48(4):1681-1684.

[4]Delaere,Iadevaia K,Heylen M,et al.Statistical energy analysis of acoustic noise and vibration for electric motors:transmission from air gap field to motor frame[C].Thirty-Fourth IEEE Annual Meeting on Industry Applications,1999,3:1897-1902.

[5]Eversman W,Burns S,Pekarek S,et al.Noise generation mechanism in claw pole alternators[J].Journal of Sound and Vibration,2005,283:369-400.

[6]Finnveden S.A quantitative criterion validating coupling power proportionality in statistical energy analysis[J].Journal of Sound and Vibration,2011,330(1):87-109.

[7]Sgard F,Nelisse H,Atalla N,et al.Prediction of the acoustical performance of enclosures using a hybrid statistical energy analysis:Image source model[J].Journal of the Acoustical Society of America,2010,127(2):784-795.

[8]Zhang Yimin,Wen Bangchun,Liu Qiaoling.Uncertain responses of rotor-stator systems with rubbing[J].JSME International Journal Series C-Mechanical Systems Machine Elements and Manufacturing,2003,46(1):150-154.

[9]MTiwari,KGupta.Effect of radial internal clearance of a ball bearing on the dynamics of a balanced horizontal rotor[J].Journal of Sound and Vibration,2000,238(5):723-756.

[10]黄允凯,胡虔生,朱建国.顾及旋转铁耗的高速爪极电机三维磁热耦合分析[J].电工技术学报,2010,25(5):54-60.Huang Yunkai,Hu Qiansheng,Zhu Jianguo.Magneto-thermal analysis of a high-speed claw pole motor considering rotational core loss[J].Transactions of China Electrotechnical Society,2010,25(5):54-60.

[11]鲍晓华,王群京,倪有源,等.汽车用爪极发电机的电磁建模及参数优化技术[J].电工技术学报,2008,23(10):23-27.Bao Xiaohua,Wang Qunjing,Ni Youyuan,et al.Electromagnetic modeling and parameter optimization of claw-pole alternator for automobile application[J].Transactions of China Electrotechnical Society,2008,23(10):23-27.

[12]Ginsberg J H.Mechanical and structural vibrations:theory and applications[M].New York:Wiley,2001.

[13]Le Bot A,Cotoni V.Validity diagrams of statistical energy analysis[J].Journal of Sound and Vibration,2010,329(2):221-235.

[14]Cai Lixun,Jin Lei,Bao Chen.On fracture mechanics testing technique based on compliance of specimens[J].Key Engineering Materials,2008,385-387:293-296.

[15]Jacek F Gieras,Chong Wang,Joseph Cho Lai.Noise of polyphase electric motors[M].New York:CRC,2006.