超声波电机黄金分割自适应转速控制

史敬灼 尤冬梅

（河南科技大学电子信息工程学院 洛阳 471003）

1 引言

主要由于特殊的机电能量转换、传递机理及电机与其驱动电路之间的相互影响，超声波电机（USM）的运行呈现明显的非线性，且运行特性的时变严重[1-5]。加之，超声波电机的定子振动、定转子间摩擦等内部状态难于实时在线观测，这都使得超声波电机的运动控制不易达到理想性能，且具有明显不同于传统电磁电机的控制特点。

已有多种适用于超声波电机转速或位置控制的控制策略被提出[1,2,6-11]。目前，超声波电机的控制，逐渐形成了这样的格局[2]：一方面，对于低成本或性能期望较低的应用场合，常规PID 控制器是首选的控制方式；这主要是因为常规PID 控制器设计方法成熟、结构简单、在线计算量小，因而实现成本低。另一方面，对于性能要求较高的应用场合，超声波电机的控制策略应是自适应的，以及时、准确地应对超声波电机明显的非线性运行特征。这里所说的自适应，是指广义的自适应，即能够根据超声波电机的当前特性来实时改变控制器结构和/或控制参数的控制方式，也包括神经网络等智能控制策略。适当设计的自适应控制策略，能够明显改善系统性能，提高控制鲁棒性。但是，这些控制策略的计算复杂度通常远高于常规PID 控制，也就需要具有更高实时计算能力的实现方式，成本较高。因而，在线计算量尽量小的有效自适应控制策略，是当前超声波电机运动控制研究的核心问题。

本文建立了两相行波超声波电机的特征模型，该模型以转速控制误差为输出，输入为用来控制电机转速的驱动频率值。随后采用该模型，给出了超声波电机的黄金分割转速控制算法，其在线计算量与PID 控制器相当，但调试++相对简单、适应能力更强。进一步，增加自适应环节，给出改进的黄金分割自适应控制策略，同样具有在线计算量相对较小的优点。实验表明，所提控制策略控制性能良好，具有鲁棒性。

2 超声波电机的特征模型

超声波电机的模型通常是其控制器设计的基础。由于超声波电机能量转换及传递过程的复杂性，以控制器设计为目的的超声波电机模型多采用辨识建模的方法，得到电机的低阶差分模型。辨识理论表明，辨识得到的低阶模型只是对实际电机的近似，采用适当方法建立的模型能够反映超声波电机的主要特征，但不是全部特性。这也就使得基于该模型设计出的控制策略具有某种近似性。

特征模型是我国航天控制专家吴宏鑫院士在辨识模型基础上提出的一种控制模型形式[12]。特征模型是一种包含在线辨识的低阶模型，其建模过程不仅同辨识建模一样考虑对象特性及扰动特性，而且还与控制性能要求相关，不同性能要求对应于不同阶次、结构的低阶模型。尤其重要的是，理论上已经证明，在任意时刻，在线辨识的特征模型都与高阶的实际对象等价，而不是近似。这就使得基于特征模型的控制器设计有可能在保持系统稳定的前提下，得到相对较好且更为稳健的控制性能。

考虑设计黄金分割转速控制器的需要，建立如下形式的超声波电机三阶特征模型，该模型以转速误差为输出，以驱动频率为输入

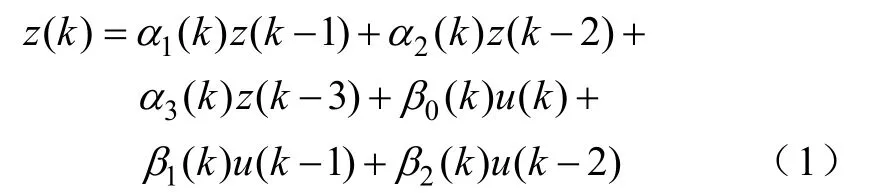
式中z(k)——转速误差，z(k)=yr(k)-y(k)；

u(k)——驱动频率；

z(k-n)——前n时刻的转速误差；

u(k-n)——前n时刻的驱动频率；

α1(k)、α2(k)、α3(k)、β0(k)、β1(k)、β2(k)——时变的特征模型参数；

yr(k)——转速给定值；

y(k)——实际转速值。

特征模型的建模过程，主要包括确定式（1）中时变模型参数的初值，确定在线递推辨识算法及其参数初值。利用实测数据，采用最小二乘一次完成辨识算法进行离线辨识，得到式（1）模型参数α1、α2、α3、β0、β1、β2依次为-1.2373、0.22685、0.11243、11.167、-19.286、8.1179，作为这些时变参数的初值。为了选择合适的在线递推辨识算法，分别采用递推最小二乘(RLS)、递推增广最小二乘(RELS)、递推极大似然(RML)等算法进行离线递推计算，得到模型输出与实测输出的误差平方和依次为105.89、106.82、107.244。由此，选择误差最小的递推最小二乘辨识算法。该辨识算法中，时变的权系数矩阵P影响辨识过程中模型参数的修正速率，该矩阵的初始取值P(0)直接影响超声波电机的起始控制性能。本文利用实验数据进行离线的循环递推辨识计算，取循环递推计算结束时的P矩阵数值作为P(0)。限于篇幅，具体建模方法不再详述，读者可参阅文献[13]，该文给出了以转速为输出的超声波电机特征模型的建模方法。

图1 为所建特征模型的输出（转速误差）与实测数据的对比，图中曲线为给定转速为90r/min的转速阶跃响应过程。如图1 所示，模型输出与实测数据相当接近，即所建特征模型能够准确逼近超声波电机的运行特性。

图1 模型输出与实测数据的对比（yr=90r/min）Fig.1 Comparison between model output and tested data(yr=90r/min)

3 超声波电机转速的黄金分割控制

3.1 黄金分割控制策略

基于上述超声波电机特征模型，构建黄金分割控制器

式中，L1、L2为黄金分割系数，分别为0.382、0.618。

可以看出，式（2）所示黄金分割控制器，直接来自于特征模型，只是增加了两个常数L1和L2，用来调整动态响应过程。这也就意味着，完成超声波电机特征模型的建模，也就完成了黄金分割控制器的设计。

若式（2）中的特征模型参数α1(k)、α2(k)、α3(k)、β0(k)、β1(k)、β2(k)取为固定值（即参数初值），可称之为固定参数黄金分割控制器。若如上所述，进行特征模型参数的在线辨识，并实时调整式（2）中的相应参数值，则成为黄金分割自适应控制器。

利用电机特征模型式（1），对超声波电机黄金分割转速控制进行了仿真分析。仿真结果表明了该控制策略的有效性。

3.2 超声波电机黄金分割转速控制的实验研究

设计超声波电机驱动控制系统进行转速控制实验，图2 为系统结构框图。实验所用电机为Shinsei USR60 两相行波超声波电机，光电编码器E 与电机转轴刚性连接，提供转速反馈信号。驱动电路为MOSFET 构成的两相H 桥结构[14]，控制电路以低成本DSP 芯片DSP56F801 为核心，辅以相移PWM 信号发生器，实现对驱动电路中MOSFET 开关状态的控制。

图2 黄金分割转速控制系统结构Fig.2 Structure of golden section speed control system

图2 中虚线框内的部分，是本文所述黄金分割转速控制器，其输出控制量为上述的驱动频率值，通过PWM 信号发生器实现对电机驱动电压频率的实时调节。对于固定参数黄金分割控制策略，图2中“特征模型参数在线辨识”环节应删去。该系统还包含两相驱动电压幅值的闭环控制，以消除超声波电机两相特性不同导致的驱动电压幅值差异，实现电压幅值的可控、可调，并抑制电压幅值随频率的变化。图2 中Uref为电压幅值的给定值，实验中设定为峰-峰值300V。

编写DSP 程序，实现上述设计的黄金分割转速控制。在实验用电机的可调转速范围内，设定不同的转速给定值，分别进行固定参数和自适应黄金分割转速控制的阶跃响应实验，图3～图6 给出了两种控制策略在空载和加载0.2N·m 情况下的阶跃响应曲线，与之对应的控制性能指标对比见表1。

图3 实测转速阶跃响应（固定参数，空载）Fig.3 Step response of speed(fixed parameters,no load)

图4 实测转速阶跃响应（固定参数，加载0.2N·m）Fig.4 Step response of speed(fixed parameters,load)

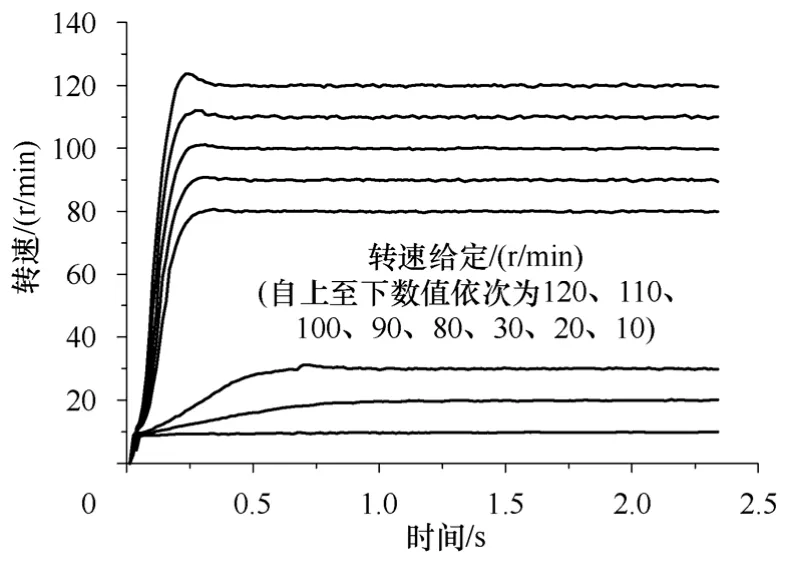
图5 实测转速阶跃响应（自适应，空载）Fig.5 Step response of speed(adaptive,no load)

图6 实测转速阶跃响应（自适应，加载0.2N·m）Fig.6 Step response of speed(adaptive,load)

表1 固定参数与自适应黄金分割控制的性能指标对比Tab.1 Comparison of control performance between fixed parameters and adaptive golden section controllers

由上述图、表可以看出，采用固定参数和包含在线辨识的自适应黄金分割控制器，均可使电机在转速可调范围内稳定运行。两种控制器均在部分转速范围内存在超调，自适应控制在低速30r/min 情况下的超调略小于固定参数控制器，但在高速110、120r/min 时，固定参数控制器超调较小。空载情况下，两种控制器的调节时间相当；由空载变为加载，固定参数控制的调节时间总体增大，而自适应控制则总体减小，从一个侧面体现了自适应控制的鲁棒性。两种控制器作用下，阶跃响应的稳态误差均因加载而增大，但自适应控制的稳态误差总体小于固定参数情况。

3.3 固定参数黄金分割控制与PID 控制的比较

如引言所述，固定参数的常规PID 控制器广泛应用于低成本的超声波电机运动控制系统中。式（2）所示固定参数黄金分割控制器的在线计算量与数字形式的常规PID 控制器相当，本节对这两种控制器进行比较。

常规PID 控制器通常根据实测响应数据，采用工程设计法进行离线设计，随后进行在线的参数整定。超声波电机非线性明显，不同转速情况下的特性差异较大；其PID 控制参数整定过程，通常是在特定转速情况下反复调整P、I、D 三个控制参数，使该转速情况下的控制性能附和期望，并将得到的控制参数值用于其他所有转速情况。因需要调整三个控制参数，在线调试工作量较大，且由于超声波电机不同转速运行的差异显著，在某一转速情况下整定的控制参数不能保证所有转速情况下的良好控制效果，甚至可能导致系统发生振荡等异常情况。

将图2 所示系统的转速控制器更换为PID 控制器，系统其他环节及实验电机不变，在给定转速为30r/min 情况下进行PID 控制参数在线整定，并将所得控制参数用于其它转速，得阶跃响应实验结果如图7 所示。当转速给定值为120r/min 时，电机无法起动；而110、100r/min 情况下，电机起动后，转速瞬间跌落至0；转速给定值90r/min 时，出现明显振荡。只是在30r/min 附近的区域，控制效果较为理想。

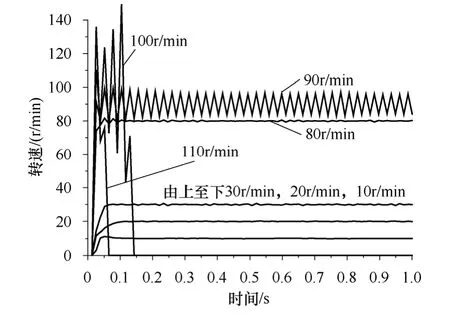
图7 实测转速阶跃响应（PID 控制器，空载）Fig.7 Step response of speed(PID controller,no load)

由此可以看出，对于超声波电机这种非线性显著的控制对象，PID 控制参数需要经过大量在线调试，才有可能保证整个调速范围内的正常运行，而最终的控制效果必然是在保证正常运行前提下的一种折中。

比较而言，固定参数黄金分割控制器的设计过程需要离线辨识得到特征模型，较PID的设计过程复杂。但其在线调试过程简单，能够保证超声波电机在整个转速可调范围内的正常运行，且整体控制效果相对较好，可以用于低成本的超声波电机控制系统中，作为PID 控制器之外的另一种可行选择。

4 黄金分割自适应转速控制策略的改进

如上所述，引入特征模型参数的在线辨识，构成黄金分割自适应转速控制器，使控制性能趋好，并具有一定的鲁棒性。但图5、图6 响应过程也还存在不如意之处，主要表现在部分响应过程存在超调、低速情况下的调节时间明显较长。

控制器输出控制量（驱动频率）的变化过程，直接决定了超声波电机转速的响应曲线。考察图8所示转速给定值为30r/min 和120r/min 时的阶跃响应和控制量变化曲线，若转速给定值30r/min 时的控制量变化更迅速，则调节时间会减小；若转速给定值120r/min 时的控制量在接近给定值时减缓变化速率，则可能使超调减为0。

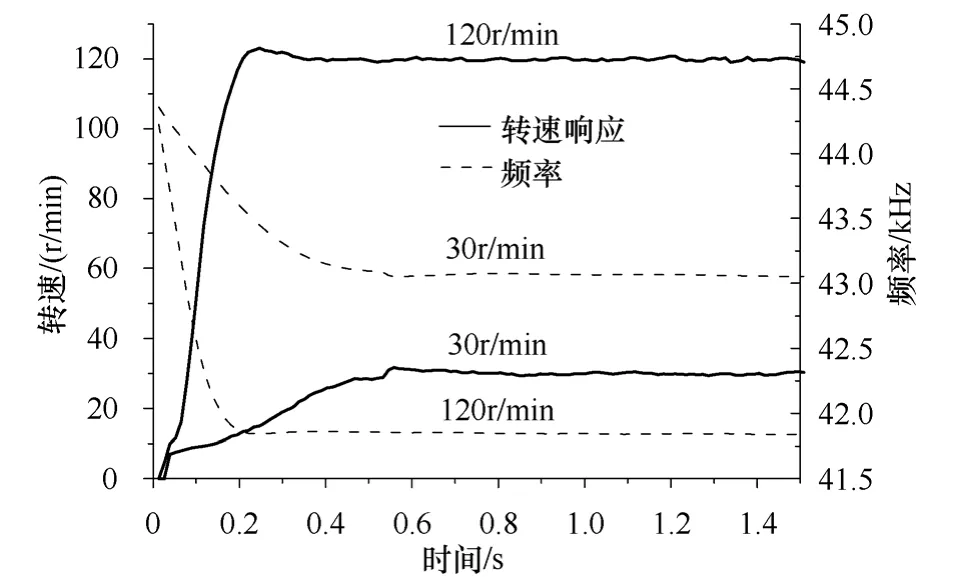
图8 实测转速阶跃响应与控制量变化过程（自适应，加载0.2N·m）Fig.8 Step response of speed and the change process of control variable(adaptive,load)

据此，考虑在黄金分割自适应控制策略中增加逻辑积分与微分控制律，即将转速控制器改进为图9 所示结构。

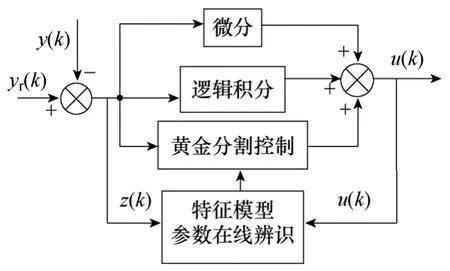
图9 改进的黄金分割自适应控制器Fig.9 Improved adaptive golden section controller

构造逻辑积分控制律

式中，ui(k)、ui(k-1)分别为当前和前一时刻的逻辑积分控制量；ci和ki为可调系数。

当输出误差z(k)在正向或负向增大，即有z(k)[z(k)-z(k-1)]＞0，则需要增强积分作用使z(k)快速下降，此时可取ki为较大值k2（常数）；反之，应减小积分作用以避免超调，可令ki=0。

ci用来在必要的时候立即去除积分作用。正常积分时，取ci为1，不需要积分时为0。即有

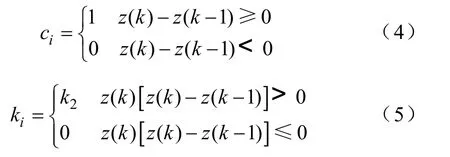
构造微分控制律

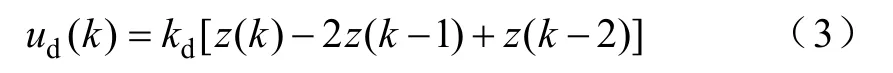
式中，ud(k)为当前时刻的微分控制量，kd为可调系数；k2和kd的取值，均在离线仿真基础上，经实验整定。

图10、图11 给出了改进控制策略在空载和加载0.2N·m 情况下的阶跃响应曲线，与之对应的控制性能指标见表2。因为所有转速响应曲线均无超调，所以表2 未列出超调数值。

图10 实测转速阶跃响应（改进自适应，空载）Fig.10 Step response of speed(improved adaptive controller,no load)

图11 实测转速阶跃响应（改进自适应，加载0.2N·m）Fig.11 Step response of speed(improved adaptive controller,load)

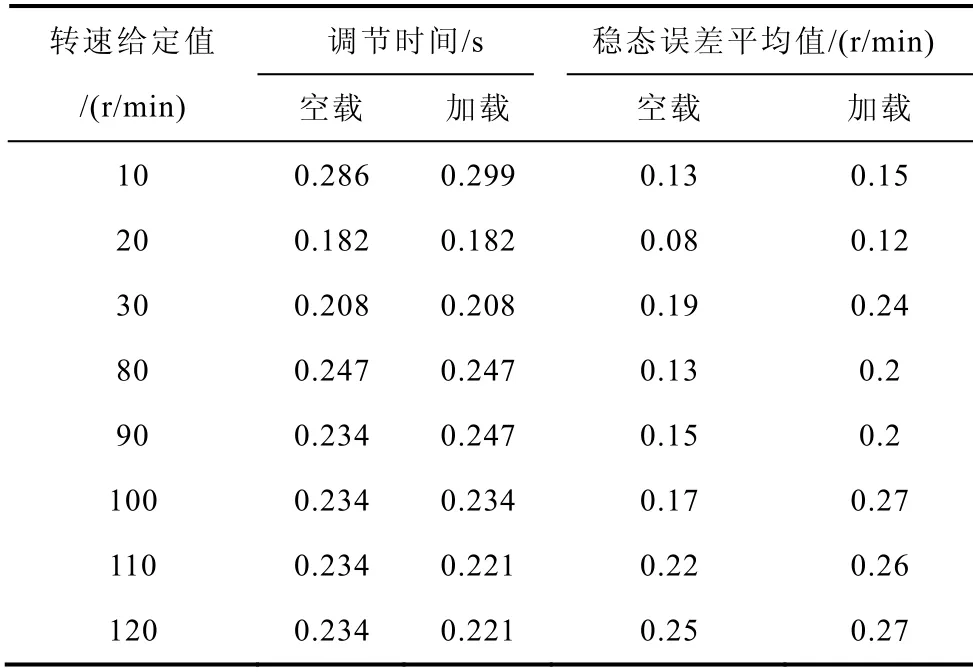
表2 改进的自适应控制的性能指标Tab.2 Performance of improved adaptive controller

由上述图表可知，不同转速情况下的调节时间接近一致，低速10～30r/min的调节时间明显减小。空载与加载对比，各转速调节时间相差不大，稳态误差平均值稍微有所增大，但变化量很小。表明改进的自适应控制器鲁棒性较好。

将表2 与表1 黄金分割自适应控制器的性能指标进行对比，改进的自适应控制对于所有转速均无超调，调节时间明显加快，稳态误差平均值相差不大。

图12 给出了改进的黄金分割自适应控制与自适应控制的调节过程对比。改进的自适应控制器是在黄金分割自适应控制器的基础上增加了逻辑积分控制律和微分控制律，意在抑制响应超调，并希望缩短调节时间。

图12 控制性能对比（转速给定值120r/min）Fig.12 Comparison of control performance

当采用黄金分割自适应控制器时，即图中虚线1（转速）和1’（频率）所示响应过程，从a 点开始出现超调，出现超调后理应减小控制量以抑制超调，但图中虚线1’在a’点后还在减小，直到b’点，从而导致转速超调。

采用改进的黄金分割自适应控制器，即图中实线2、2’所示响应过程，由于微分控制律的作用，使控制量不至于过大而引起超调。与曲线1’相比，曲线2’所示控制作用较小，所以a 到b 之间的转速超调得到有效抑制。在该控制过程中，逻辑积分控制律在出现超调后起作用，在a、b 点之间，误差变化量呈增大趋势，逻辑积分控制作用加强来抑制该变化趋势。观察图中实线2’，在a’、b’之间，控制量逐渐增加来减小超调；在b、c 点之间，误差变化量呈减小趋势，转速响应曲线越来越逼近转速给定值，逻辑积分控制作用适当减小，如图实线2’控制量在b’、c’之间稍有减小，故转速响应曲线2 没有出现超调，且调节时间减小。

5 结论

在建立超声波电机特征模型的基础上，给出了固定参数黄金分割控制器和黄金分割自适应控制器两种超声波电机转速控制器，并通过对实验结果的分析，给出了逻辑积分和微分控制律等控制策略改进措施，实验表明了所提控制策略的有效性。本文工作表明：

（1）固定参数黄金分割控制器的整体控制效果优于常规PID 控制器，在线计算量相当，可用于性能要求不高的场合。

（2）包含在线辨识的黄金分割自适应控制策略的控制性能，优于固定参数控制策略，且具有更好的鲁棒性。

（3）仿真和实验均表明，最小二乘辨识算法能较好地适应超声波电机模型在线辨识需求。因特征模型阶次低，在线辨识导致的控制策略计算量增加不大。

[1]赵淳生.超声电机技术与应用[M].北京:科学出版社,2007.

[2]史敬灼.超声波电机运动控制理论与技术[M].北京:科学出版社,2011.

[3]Chen Weishan,Shi Shengjun,Liu Yingxiang,et al.A new traveling wave ultrasonic motor using thick ring stator with nested PZT excitation[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,2010,57(5):1160-1168.

[4]顾菊平,胡敏强,金龙,等.基于 MCM的环型行波超声波电机驱动集成单元的热分析[J].电工技术学报,2010,25(2):49-53.Gu Juping,Hu Minqiang,Jing Long,et al.Thermal analysis of driving-unit for ring-type traveling-wave ultrasonic motor based on MCM[J].Transactions of China Electrotechnical Society,2010,25(2):49-53.

[5]蒋春容,胡敏强,金龙,等.行波型超声波电机定转子接触粘滑分布特性[J].电工技术学报,2010,25(12):48-53.Jiang Chunrong,Hu Minqiang,Jing Long,et al.Stick-slip distribution of contact area between stator and rotor in traveling wave ultrasonic motor[J].Transactions of China Electrotechnical Society,2010,25(12):48-53.

[6]史敬灼,张慧敏.行波超声波电机Lyapunov 模型参考自适应转速控制[J].电工技术学报,2011,26(4):44-50.Shi Jingzhuo,Zhang Huimin.Model reference adaptive speed control of ultrasonic motor based on Lyapunov theory[J].Transactions of China Electrotechnical Society，2011,26(4):44-50.

[7]Shi J,Liu B.Optimum efficiency control of traveling wave ultrasonic motor system[J].IEEE Transactions on Industrial Electronics,2011,58(10):4822-4829.

[8]Giraud Frédéric,Lemaire Semail Betty,Aragones,Julien,et al.Precise position control of a traveling-wave ultrasonic motor[J].IEEE Transactions on Industry Applications,2007,43(4):934-941.

[9]Yoshida Tomohiro,Senjyu Tomonobu,Nakamura Mitsuru,et al.Position control of ultrasonic motors using dead-zone compensation with fuzzy neural network[J].Electric Power Components and Systems,2006,34(11):1253-1266.

[10]Faajeng L,Syuanyi Chen,Pohuan Chou,et al.Interval type-2 fuzzy neural network control for X-Y-Theta motion control stage using linear ultrasonic motors[J].Neurocomputing,2009,72(4-6):1138-1151.

[11]Senjyu T,Kashiwagi T,Uezato K.Position control of ultrasonic motors using MRAC and dead-zone compensation with fuzzy inference[J].IEEE Transac-tions on Power Electronics,2002,17(2):265-272.

[12]吴宏鑫,胡军,谢永春.基于特征模型的智能自适应控制[M].北京:中国科学技术出版社,2008.

[13]尤冬梅,史敬灼.超声波电机特征模型的辨识建模[J].微特电机,已录用.You Dongmei,Shi Jingzhuo.Identification of ultrasonic motor’s characteristic model[J].Micro & Special Motor,Accepted.

[14]王海彦,史敬灼.基于CPLD的超声波电机H 桥相移PWM 控制[J].电气自动化,2009,31(2):48-50.Wang Haiyan,Shi Jingzhuo.Ultrasonic motor’s phase-shift PWM control based on CPLD[J].Electrical Automation,2009,31(2):48-50.