低压断路器振动特性分析与合闸同期性研究

缪希仁 王 燕

（福州大学电气工程与自动化学院 福州 350108）

1 引言

断路器振动信号含有丰富的机械特性信息，且具有非侵入式状态监测特点，在该领域国内外研究人员已开展了大量有关断路器机械故障诊断的理论研究[1,2]。文献[3]提出基于小波变换的信号奇异性检测理论处理振动信号，并提出小波变换故障特征参数的多尺度提取方法，即利用信号包络小波变换各尺度上模极大值的传递性计算奇异性指数，且取得较为实用的效果；文献[4]利用小波包和短时能量分析的方法处理振动信号，分析高压断路器合闸同期性且取得良好的效果；文献[5]试验表明，同类型的断路器动作时所产生的振动信号相似，这就使通过比较同种类型不同断路器的振动信号检测断路器故障成为可能，使基于振动信号所进行的断路器状态检测和故障诊断推广性与实用性得到进一步提高。

三相同期性是断路器重要的机械特性参数之一。断路器因多次合闸及分断保护主回路产生的触头磨损、撞击或定期检修调整不当，都会造成断路器三相触头合闸同期性变化。当三相同期性不在容许的范围内时，会影响断路器的性能和寿命以及电网的稳定性运行，因此，断路器合闸同期性研究对其状态监测与故障诊断具有重要意义，但目前断路器同期性研究还局限在中高压断路器。随着智能配电网发展，对配电系统安全可靠性提出更高的要求，作为主要机械性能指标的低压断路器的同期性研究显得十分必要。

小波包能量谱[6-8]分析技术，具有对振动信号高频部分更精细的分解能力，其小波包重构可用于断路器振动信号的频带能量分布情况分析，由于不同合闸同期性状态具有不同的振动信号的频带能量分布，由此可识别断路器合闸不同期性故障状态。低压断路器电动式操作机构具有在电机驱动结束后断路器立即合闸的特点，利用驱动电机的电流信号作为时间标识可有效提取合闸振动信号。因此，本文提出将小波包能量谱与操动机构电流驱动信号相结合分析与提取低压断路器合闸同期性特征矢量的新方法，并应用BP 神经网络良好的状态分类能力[9]，识别低压断路器三相不同期合闸故障。

2 振动信号小波包能量谱分析技术

小波包变换具有任意多尺度分解的特性，它对小波变换未分解的高频部分进行更精细的分解，并且该分解无冗余，从而可根据信号特性和分析要求，在一定频域范围内提高频率分辨率，在一定时间范围内提高时间分辨率，从而弥补了小波变换因为频率分辨率随频率升高而降低所导致的“高频低分辨率”问题。本文针对低压断路器振动信号特性，采用三层的小波包分解[10]如图1 所示的二叉树分解结构，其中节点(0,0)代表原始信号S，节点(i,j)代表小波包分解的第i层（i为分解尺度）第j个频带信号分量Sij(i=1,2,3;j=0,1,2,…,7)。其中每一层都覆盖信号所有频率，但各层分辨率不同；分解层数越多，频域分辨率越高；其三层小波包分解关系为

图1 三层小波包分解Fig.1 Three layer wavelet packet decomposition

此外，式（1）小波包分解的各节点系数重构算法可详见文献[10]。小波包分解各节点重构的信号，表示该节点所对应频带分量在原始信号中的分布情况，实现了对原始信号的频域抽取，可反映故障状态特征频率的变化。

本文应用小波包分解与重构原理，提取断路器振动信号特征矢量的步骤如下：

（1）选择适当的小波函数对振动信号进行三层小波包分解。因为振动信号分解质量的好坏很大程度上依赖于所选的基波函数，评价所选的基函数可以用信息代价函数来描述。本文针对低压断路器振动信号选用db5 小波函数，并以适用于振动信号分析的Shannon 信息熵[11]为标准进行小波包分解。

（2）分别对各频率范围的小波包分解系数进行重构。本文只对式（1）小波包的第三层8 个节点进行分析，因最大频率为8kHz（见图2，振动信号频率范围为0～8kHz），则每个节点代表1kHz的频率范围，经小波包分解系数重构分别提取振动信号从低频到高频8 个频带上的信号特征。

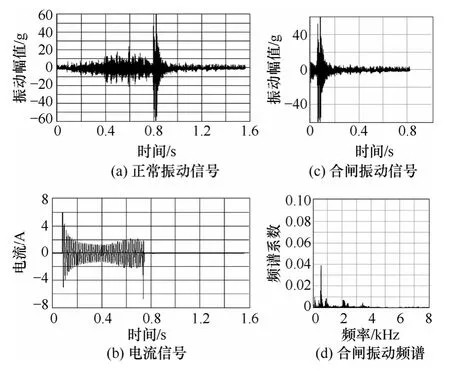
图2 正常振动合闸信号Fig.2 Normal vibration closing signal

（3）求振动信号分布在各个频带中的能量。设节点S3j(j=0,1,…,7)对应的能量为E3j(j=0,1,…,7)，在上述各频带信号特征提取的基础上，计算各个频段的能量。

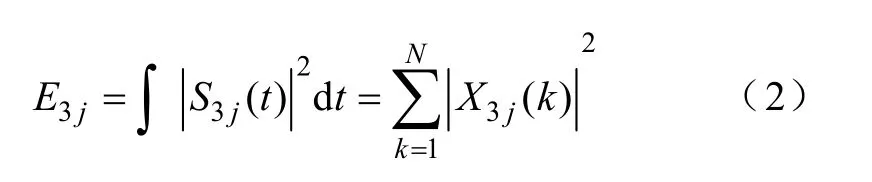
式（2）的含义为一个信号在时域的能量与频域的能量相等。式中X3j（k）（j=0,1,…,7；k=1,2,…,N）表示小波包重构信号各离散点的幅值，N为采样点数。

（4）构造特征矢量。低压断路器合闸过程三相不同期发生时，各频带内信号特征会有相应变化，本文以频带能量谱构造一个特征矢量

由于低压断路器振动信号各频带能量相差较大，为了便于比较三相不同期状态下各个频带能量及其数据分析，将各频带能量归一化处理

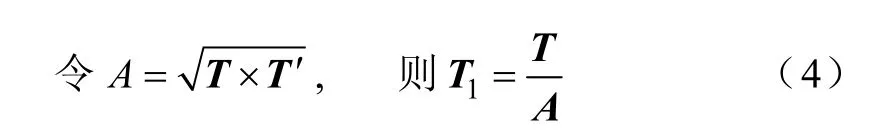
因此，矢量T1即为归一化后的低压断路器振动信号能量谱特征矢量。

3 有效振动信号的提取

本文针对电动机操作机构的低压断路器，在电机驱动结束后断路器立即合闸的特点，以电机电流信号结束为振动信号提取的时间标识点，以限定断路器合闸过程触头碰撞时振动信号的提取范围，为合闸过程三相同期性分析提供更有效的振动信号区间。

本文以 DW15—1600 万能式断路器为试验样机，将单个振动加速度传感器安装在断路器基座横梁上，其检测的振动方向与触头合闸撞击方向一致，在空载条件下采集反映三相同期性状态的触头合闸振动信号，并将振动信号采样频率设置为16kHz，采样数据点数为40000。

根据 DW15—1600 万能式断路器出厂技术要求，当触头厚度低于2mm 时应予以更换。在断路器正常合闸振动试验基础上，本文通过调整触头的开距和超程，分别模拟三相触头机构磨损或调整不当造成的各种合闸不同期性状态。以电机驱动电流结束为振动信号提取标识点，本文分别对低压断路器A、B、C 相触头磨损造成的不同期故障进行振动信号检测试验，获得的合闸振动信号及对应的傅里叶变换频谱分析如图3 所示。

图3 合闸不同期振动信号及频谱图Fig.3 Vibration signal & spectrum diagram of closing asynchronous

由图2 和图3 可以看出，低压断路器正常合闸及A、B、C 三相分别存在不同期合闸时，其各频带内振动信号特征有相应变化，因此，利用前述小波包能量谱分析技术，对图2c 和图3的振动信号分别计算得出4 种合闸同期性状态归一化后各频段能量谱特征矢量柱状图如图4 所示。

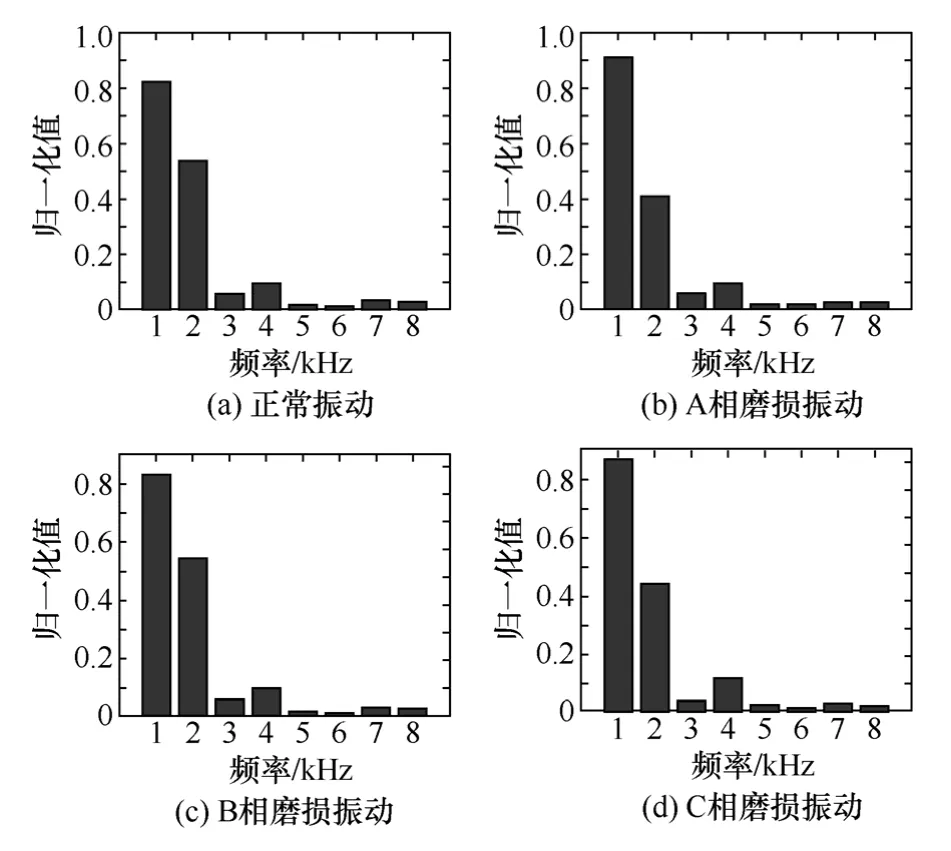
图4 振动信号频带能量柱状图Fig.4 Vibration signal frequency band energy column

4 三相不同期故障神经网络识别

本文利用多次断路器正常合闸状态的振动信号和三相同期故障合闸状态（分别为A 相不同期、B相不同期、C 相不同期）的振动信号来进行小波包分解及重构，然后提取相应的振动信号在各个频带的能量谱特征矢量作为BP 神经网络的输入矢量，并选用trainlm 函数（Levenberg-Marquardt 优化方法）训练BP 网络，以建立低压断路器三相不同期故障识别模型。其神经网络训练和测试数据分别用矢量（000）表示正常状态，（001）表示A 相触头不同期故障，（010）表示B 相触头不同期故障，（011）表示C 相触头不同期故障，从而建立基于振动信号能量谱特征矢量及BP 神经网络的断路器三相不同期故障识别模型。

本文以正常、A 相不同期、B 相不同期及C 相不同期合闸振动信号的各频带能量特征矢量为神经网络输入，以低压断路器三相合闸同期或不同期的上述4 种类型同期性状态为神经网络输出，建立低压断路器三相不同期故障识别模型，表1 为部分训练样本数据（限于篇幅，每种状态仅列出三次试验数据），表2 为测试样本数据。

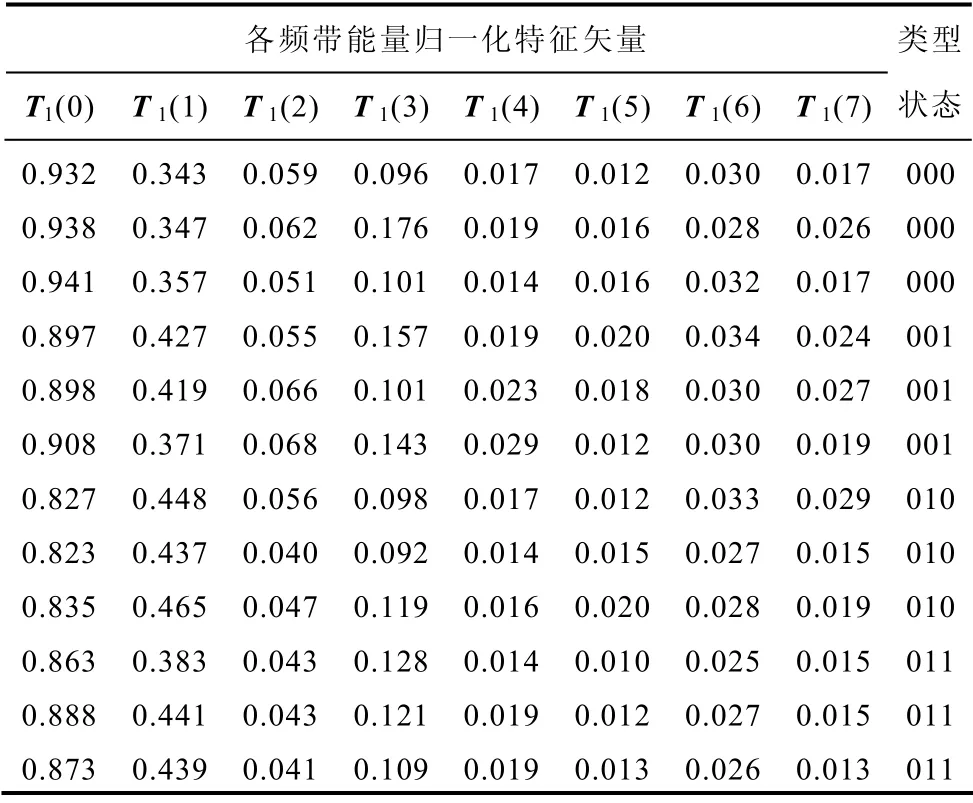
表1 部分训练样本Tab.1 Part of train samples

表2 测试样本Tab.2 Testing samples

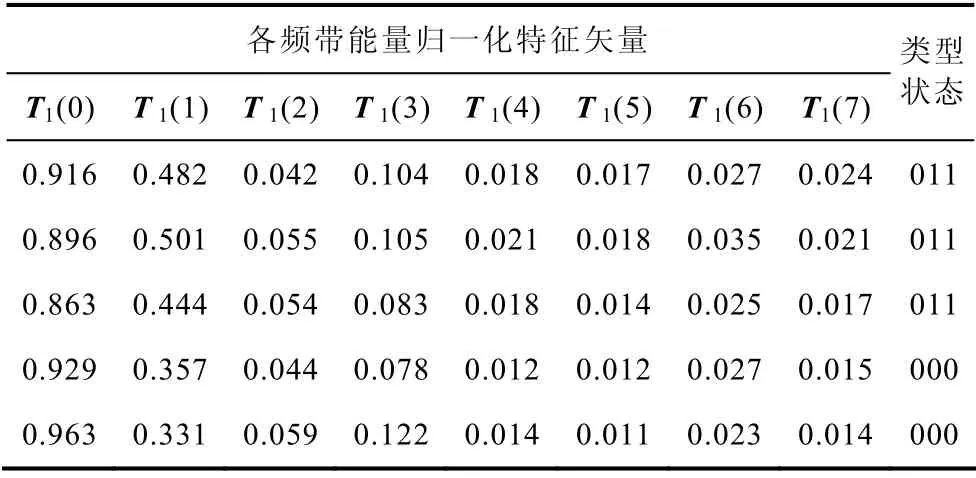
（续）

本文在BP 神经网络中采用trainlm 函数，是依据Levenberg-Marquardt 优化理论，并利用误差函数的近似二阶导数信息对网络的权值和阈值进行调整，克服采用梯度下降反向传播算法的BP 网络通常具有的收敛速度慢、易陷入局部极小点等缺点。使用trainlm 函数的训练过程如图5 所示，图中实线为训练过程，虚线为目标值。其训练结果见表3。

图5 trainlm 函数的训练过程Fig.5 Trainlm training process

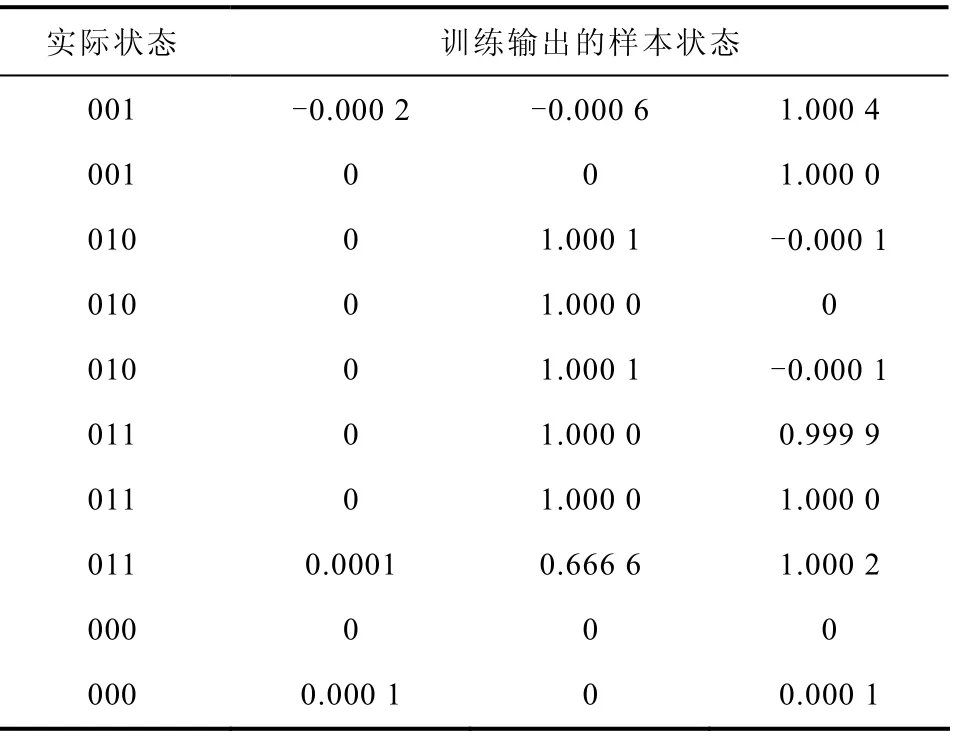
表3 trainlm 函数的训练结果Tab.3 Testing result of trainlm fuction

由图5 与表3 可以得出，使用trainlm 训练函数的BP 神经网络迭代9 次后就达到了收敛要求，即本文建立的基于振动信号小波包能量谱分析的神经网络模型，可有效识别低压断路器三相合闸不同期性故障。

5 结论

（1）以操动电机驱动电流信号结束点作为提取合闸振动信号的标识，可有效提取及限定断路器合闸时振动信号的分析范围。

（2）低压断路器三相合闸同期性发生变化时，引起振动信号的时频域分量相应变化，利用小波包分解与重构可有效提取各种三相同期性状态的能量谱故障特征矢量。

（3）小波包能量谱与神经网络相结合，可对机构磨损或调整不当造成的各种合闸同期性状态加以有效识别。

[1]杨飞,王小华,荣命哲,等.一种新的中压真空断路器三相同期在线监测方法[J].中国电机工程学报,2008,28(12):139-144.Yang Fei,Wang Xiaohua,Rong Mingzhe,et al.A novel on-line monitoring method for three phase synchronization of medium voltage vacuum circuit breaker[J].Proceedings of the CSEE,2008,28(12):139-144.

[2]孙来军,胡晓光,纪延超.改进的小波包–特征熵在高压断路器[J].中国电机工程学报,2007,27(12):103-108.Sun Laijun,Hu Xiaoguang,Ji Yanchao.Fault diagnosis for high voltage circuit breakers with improved characteristic entropy of wavelet packet[J].Proceedings of the CSEE,2007,27(12):103-108.

[3]胡晓光,戴景民,纪延超,等.基于小波奇异性检测的高压断路器故障诊断[J].中国电机工程学报,2001,21(5):67-70． Hu Xiaoguang,Dai Jingmin,Ji Yanchao,et al.The fault diagnosis of high voltage breakers based on wavelet singularity detection[J].Proceedings of the CSEE,2001,21(5):67-70.

[4]马强,荣命哲,贾申利.基于振动信号小波包提取和短时能量分析的高压断路器合闸同期性的研究[J].中国电机工程学报,2005,25(13):150-154.Ma Qiang,Rong Mingzhe,Jia Shenli.Study of switching synchronization of high voltage breakers based on the wavelet packets etractional gorithm and short time analysis method[J].Proceedings of the CSEE,2005,25(13):150-154.

[5]Runde M,Skyberg B,Ohlen M.Vibration analysis for periodic diagnostic testing of circuit breakers[C].High Voltage Engineering Symposium,London,UK,1999:98-101.

[6]Pan Hongxia,Men Jifang.Fault diagnosis of diesel engine based on energy spectrum analysis[C].Proceedings of the International Conference on Control,2012:697-701.

[7]赵志宏,杨绍普.基于小波包变换与样本熵的滚动轴承故障诊断[J].振动、测试与诊断,2012,32(4):640-644,692.Zhao Zhihong,Yang Shaopu.Roller bearing fault diagnosis based on wavelet packet transform[J].Journal of Vibration,Measurement & Diagnosis,2012,32(4):640-644,692.

[8]徐建源,张彬,林莘,等.能谱熵向量法及粒子群优化的RBF 神经网络在高压断路器机械故障诊断中的应用[J].高电压技术,2012,38(6):1299-1306.Xu Jianyuan,Zhang Bin,Lin Xin,et al.Application of energy spectrum entropy vector method and RBF neural networks optimized by the particle swarm in high-voltage circuit breaker mechanical fault diagnosis[J].High Voltage Engineering,2012,38(6):1299-1306.

[9]Shariatinasab Reza,Akbari Mohsen,Aghaebrahimi M R.A novel wavelet-neural network method for fault location analysis on transmission lines[C].Proceedin-gs of the Mediterranean Electrotechnical Conference,2012:963-966.

[10]程正兴.小波分析算法与应用[M].西安:西安交通大学出版社,1998.

[11]李舜铭,李香莲.振动信号的现代分析技术与应用[M].北京:国防工业出版社,2008.