开放型试题AHP评分逆序问题研究

冯艳宾 马洪超

1 引言

开放型试题具有条件开放性、过程开放性、结论开放性等特征，它注重探究性和生成性的考查，能更好地考查出被试的灵活性和创造性，已被广泛地应用到语言测试和人才评估等领域中。由于开放型试题没有固定标准答案，开放型试题的评分常常带有比较明显的主观性。开放型试题评价标准的不确定性与主观性使得它的运用受到一定限制。

为克服开放性题型评分的主观性，等级描述型评定方法（SOLO分类评价法）和要素分析型评定方法（PTA量表法）已被应用到开放性考试中去（高凌飚，2004，文庆城，2005，赵利霞,2010）。SOLO分类评价法主要采用等级描述的方法，按等级标准对被评价者的整体情况进行赋值，它适用于层次分明、强调逻辑的分析型、论述型的开放型试题；PTA量表法则是一种要素分析的方法，其中的因素又分为不同等级，然后将基本单元的标定分数加总求和。PTA量表法则更适合于分类细致，操作性强，更倾向于操作性、表现性的开放型试题。在决策分析中SOLO分类评价法和PTA量表法中的等级判定和要素分析均带有很强的主观性，评分结果并不精确。层次分析法（Analytic Hierarchy Process，AHP）虽然是一种要素分析与等级相结合的方法，但AHP并非侧重将所有因素内部细分为若干个等级，而是分析因素之间的关系，注重因素在被试之间的比较，关注因素之间的权重计算。它是一种决策分析法，更适用于以选拔为目的的开放型试题。

2 层次分析法

层次分析法（Analytic Hierarchy Process，AHP）是由美国运筹学家Saaty教授提出的。其基本思想是通过分析复杂问题包含的各种因素及其相互关系，将问题所设计的全部因素按不同的层次进行分类，标出上一层与下层因素之间的关系，形成一个多层次结构。在每一层次，均按某一准则对该层因素进行相对重要性判断，构造判断矩阵，并通过解矩阵特征值，确定因素的排序权重，最后再进一步计算出各层次因素对总目标的组合权重。AHP是一种定性和定量相结合的多属性决策方法，是将决策者的经验判断进行量化决策分析的有效方法。AHP层次结构模型的构建，可分为目标层、准则层和方案层（见图1）。对从属于上一层的同层各因素，采用1～9标度进行两两比较，建立两两比较判别矩阵A。表1是两两比较矩阵的标度表。

表1 1～9标度表

构造出两两比较矩阵A后，要对矩阵A进行一致性检验，即先求出衡量两两比较矩阵A的一致性指标CI=，再基于随机一致性指标RI构造一致性比率CR=，当CR＜0.1时可以认为A的不一致程度在容许范围之内，上述公式中，λ是矩阵A的最大特征值，n是矩阵A的阶数。经一致性检验通过后，根据各个比较矩阵得出的权向量，逐层进行线性加权，计算出方案层诸方案对总目标的测评指标值，根据该测评指标的值的大小进行决策。

2.1 AHP基本步骤

下面以留学生汉语口语测评为例，说明层次分析法的分析步骤。学生的口语测评结果为目标层；准则层分为：话题描述、词语表达和朗读回答；方案层是待评价的学生。准测层中的三个测评指标的权重可通过构建判断矩阵来计算获得，在此设定话题描述的权重为50%，词语表达的权重为35%，朗读回答的权重为15%。层次分析法的过程如图1。

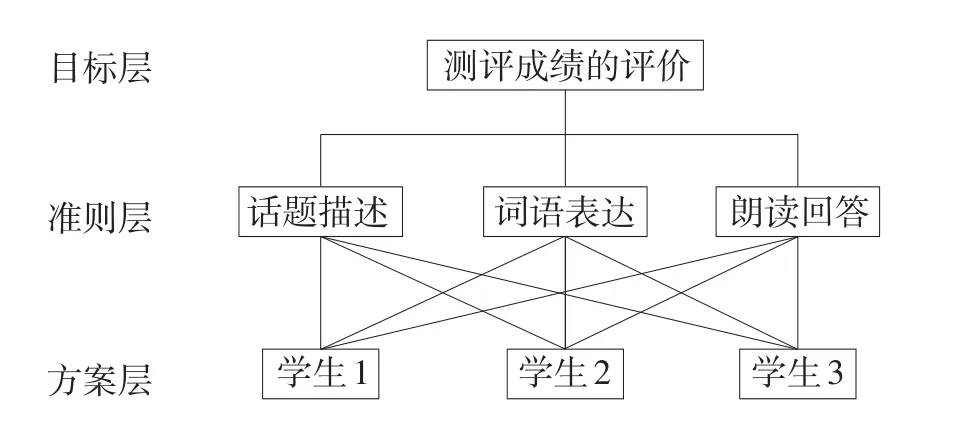
图1 留学生口语测评的层次结构

由图1的层次结构知，方案层（参加测验的学生）依次对于准则层：话题描述、词语表达、朗读回答三个测评指标进行两两比较可得出了下面三个判断矩阵（见表2）。

表2 被试学生的三个测评指标两两比较矩阵

经计算得三个矩阵的最大特征值λmax均等于3，一致性比率CR均等于0，满足一致性，说明学生的测评没有误差。话题描述准则下的比较矩阵如下：根据公式Aw=λmaxw，求得λmax对应的特征向量并归一化后得w1=(1/6,2/3,1/6)T，即方案层三个学生在话题描述准则下的权值分别为1/6,2/3,1/6。同理，可求得方案层三个学生在话语表达和朗读回答准则下的权值，结果见表3。

表3 被试学生在三个测评指标下的权值

现已知准则层三个测评准则的权重分别是50%、35%、15%，根据“线性加权和”得方案层三个学生总测评指标分别为：

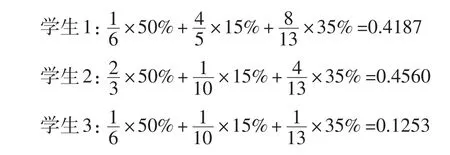
根据三个学生的总测评指标大小关系0.4560＞0.4187＞0.1253,可得三个学生的测评结果顺序为：学生2＞学生1＞学生3。

2.2 AHP评分中逆序现象

在准则层各因素权重不变的情况下，方案层被试数量的增加或减少，会带来两两比较矩阵的变化，这种变化可能会对最终的测评结果有影响。以下在方案层原有被试的基础上，增加一名学生4，设定该学生的能力特征和学生2完全一致。通过对准则层的三个测评指标进行两两比较，得出两两比较矩阵，见表4。

经检验，三个判断矩阵的最大特征值λ均等于3，一致性比率CR均等于0，满足一致性，说明对学生的测评没有误差。进一步根据各个比较矩阵的最大特征向量，求得各被试学生测评权值，见表5。

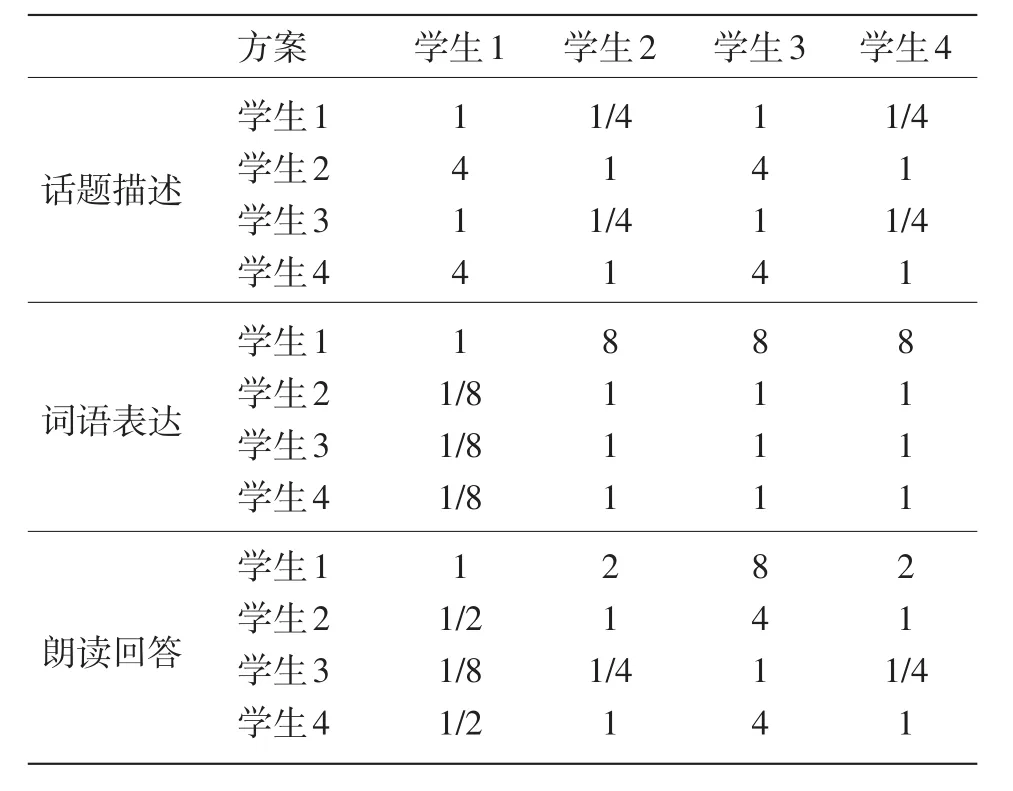
表4 增加了学生的三个测评指标两两比较矩阵

表5 被试学生在三个测评指标下的权值

根据“线性加权和”得方案层四个学生总测评指标分别为:

根据四个学生的总测评指标大小关系0.3238＞0.2960=0.2960＞0.0842，得四个学生的测评结果顺寻为学生1＞学生2=学生4＞学生3。增加了学生4，造成了学生1和学生2的测评结果顺序发生逆转。

2.3 逆序的原因和解决办法

不少文献对层次分析法中的逆序问题进行的多方面研究，面对逆序出现的各种复杂情况，解决方法也主要是根据具体类型的逆序现象提出相应的解决方案（Belton V,1983，吴江,1990，徐泽水,2004）。在单一准则下(即准则层只有一个测评指标），方案层中新方案的增加不改变原有方案的排序（汪浩，1993）。而多准则（即准则层有多个测评指标）条件下，方案层中增加新方案所带来的逆序问题是由获得总测评指标的“线性加权和”规则造成（刘奇志，1995）。设上文案例中准则层的三个测评指标的权重为α1，α2，α3，方案层三个方案分别在三个测评指标下的权值为aij（i,j=1,2,3），见表6。

表6 三个学生在三个测评指标下的权值

学生i的总测评指标Si= α1ai1+α2ai2+α3ai3（i=1,增加学生4（能力和学生2相同）后，新方案层四个学生分别在三个测评指标下的权值为i,j=1,2,3,4），见表7。这 时 ，学 生i的 总 测 评 指 标能力相同，则有

表7 四个学生在三个测评指标下的权值

在方案层增加了学生4后，由于学生1和学生2在准则层三个测评指标下的权重由aij变成了，进而通过“线性加权和”得到的总测评指标和之间的大小关系并不总与S1和S2之间的大小关系保持一致，从而造成逆序产生（汪浩，1993）。

为了克服上述由于方案层增加(或减少)新方案而带来的逆序问题，将“线性加权和”规则转换成“指数加权积”规则，即总测评指标当方案层增加新方案时，得到新的的总测评指标之间的大小关系和Si是一致的（刘奇志，1995）。

下面，采用总测评指标的“指数加权积”方法以及表3的数据，求得方案层是三个学生时的总测评指标值为：

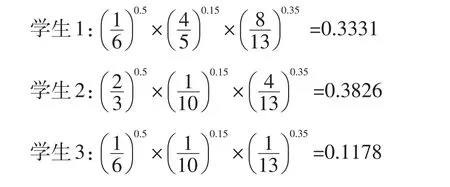
由三个学生的总测评指标值，得三个学生的优劣次序为：学生2＞学生1＞学生3。

在方案层增加学生4的情况下，采用总测评指标的“指数加权积”方法以及表5的数据,求得四个学生总测评指标值分别为：

根据四个学生的总测评指标值，得四个学生的优劣次序为：学生2=学生4＞学生1＞学生3,其中学生1和学生2的优劣关系没有发生改变。

3 结论

在决策过程中，通过引入AHP方法，可以更好地控制评分者的心理、经验、决策水平带来的误差，实现主观评价的客观化，避免由于主观原因造成的误差。但是采用总测评指标的“线性加权和”规则的层次分析法求得的评级结果会随着评价对象数量的变化而出现逆序现象，从而干扰决策者的评价结果，而采用“指数加权积”规则的层次分析法，在两两比较矩阵一致的条件下，可有效解决逆序现象，实现了评价结果的保序性。

AHP方法广泛应用与决策评价当中。在大规模考试中，随着考生数量的增加，两两比较次数会大大增加，构成的矩阵也会增大。当数量增大到一定程度时，评价者对准则把握的准确性也将降低。所以，在多测评指标的考核中，需要精细区分考生差异的优中选优时，AHP方法的效果会更好。此外，AHP法比较适合于计算各指标因子的权重，但对具体模糊指标的评定不够准确，在遇到因素众多、规模较大的问题时，判断矩阵难以满足一致性的要求。

[1] 高凌飚，吴维宁.开放型试题如何评分?——介绍两种质性评分方法[J].学科教育，2004(8):1-6.

[2] 文庆城，许应华.PTA量表法评价化学猜想与假设能力探讨[J].教学与管理,2005(6):39-40.

[3] 赵利霞.国内SOLO分类评价理论研究文献综述:1998—2008[J].江苏教育研究,2010(19):10-14.

[4] Belton V,G.T.,On a shortcoming of Saaty's method of analytic hierarchies.Omega,1983.3(11):228-230.

[5] 吴江.AHP用于方案选择时的逆序问题[J].系统工程理论与实践,1990(3):49-52.

[6] 徐泽水.AHP中新元素导入的强保序性研究[J].控制与决策,2004(4):433-436.

[7] 刘奇志.层次分析积因子方法的保序性[J].系统工程学报,1995(1):61-70.

[8] 汪浩,马达.层次分析标度评价与新标度方法[J].系统工程理论与实践,1993,13(9),24-26.