基于反步控制的PMSM转速跟踪研究
范仁凯,胡勤丰
(南京航空航天大学 自动化学院,江苏 南京210016)
1 引言
永磁同步电机由于转矩密度高、 转动惯量小、 效率高等优点而广泛应用于伺服场合。 但是永磁同步电机是一个变参数、 强耦合的非线性系统,因此常规的PID 控制通常不能满足伺服场合的高性能要求[1-3]。 针对此问题,相关学者提出滑模变结构[4]、自适应[5]、模糊[6]等具有非线性特征的控制器使系统不但能满足性能要求,还能对系统参数具有一定的自适应能力。但是以上非线性控制方法的理论复杂、 实现困难,从而限制了其在实际场合的应用。
本文结合永磁同步电机数学模型的结构特点和非线性因素,采用反步设计方法[7-8]设计一个非线性控制器,该控制器理论清晰、 结构简单、 易于实现,实验结果表明该控制器性能突出,具有很好的推广价值。
2 永磁同步电机的数学模型
表贴式永磁同步电机的dq 数学模型:
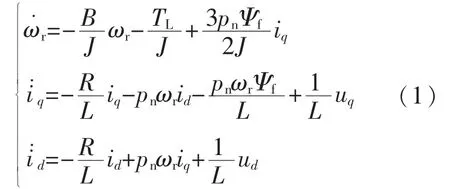
式中:ud,uq分别为定子d,q 电压;id,iq分别为定子d,q 电流;R 为定子电阻;L 为定子电感;ωr为转子机械角速度;Ψf为永磁磁链;TL为负载转矩;pn为极对数;J 为转子转动惯量;B 为粘滞摩擦系数。
3 反步控制器的设计
3.1 反步控制器设计步骤
1)将非线性系统的数学模型转化成状态方程;
2)选择子系统,定义状态的误差并将子系统状态方程转换成误差的状态方程,选取合适的输入构造李雅普诺夫函数使子系统稳定;
3)选择子系统,将前一子系统的输入作为该子系统的状态给定,定义状态的误差并将子系统状态方程转换成误差的状态方程,选取合适的输入构造李雅普诺夫函数使子系统稳定;
4)重复步骤2),3),直到反推出整个系统的输入;
5)稳定性证明。
3.2 反步控制器设计过程
1)以i*q为输入,ω*r为状态给定,根据式(1)构建子系统为
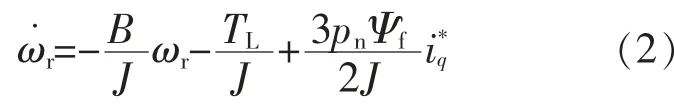
定义转速误差e1=ω*r-ωr,求导并代入式(2)可得
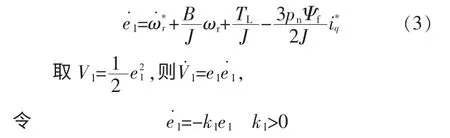
代入式(3)得子系统的控制输入为
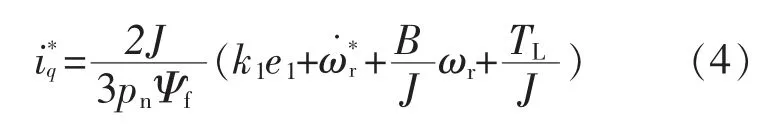
式(4)即为转速控制器ASR,它包含了一个类似于P 控制的调节项αk1e1、 加速度前馈、 粘滞摩擦转矩补偿和负载转矩补偿)。 其中,加速度前馈可加快转速的响应速度且能减小超调,粘滞转矩补偿和负载转矩补偿可在没有I 控制的条件下使稳态误差趋于零。
2)以u*q为输入,i*q为状态给定,根据式(1)构建子系统为
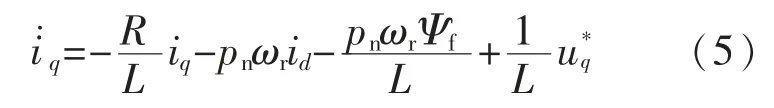
定义q 轴电流误差e2=i*q-iq,求导并代入式(5)可得:

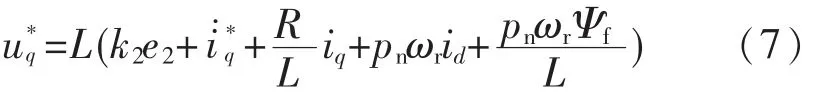
3)以u*d为输入,i*d=0 为 状态给定,根据式(1)构建子系统为
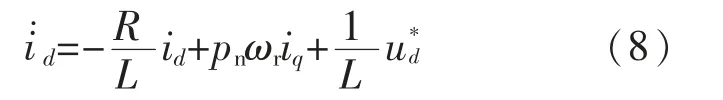
定义d 轴电流误差e3=-id,求导并代入式(8)可得:

带入式(9)得子系统的控制输入为
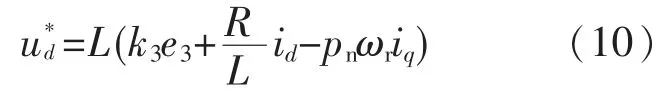
式(7)、式(10)分别为q 轴电流控制器ACR_q和d 轴电流控制器ACR_d。 与转速控制器类似,它们由调节项、前馈项(ACR_d 的前馈项为零)和补偿项组成。 其中,前馈项能加快电流的响应速度;补偿项能很好地补偿dq 轴电枢反应和永磁感应电势的影响。
4)证明系统的稳定性。

由于V2有界,根据Barbalat 引理[9]可得

根据以上设计的反步控制器,得出永磁同步电机转速控制系统的结构框图,如图1所示。
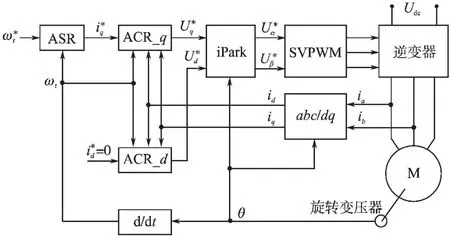
图1 永磁同步电机转速控制系统结构框图Fig.1 The control block diagram of PMSM speed control system
图1中ASR,ACR_q 和ACR_d 分别为转速控制器、q 轴电流控制器和d 轴电流控制器,他们的内部算法分别由式(4)、式(7)和式(10)决定。
4 实验验证
根据图1所示的系统结构框图搭建永磁同步电机实验平台。 平台以TI 公司的DSP TMS320F2812 为控制核心,功率器件采用三菱公司的高集成度、高可靠性的IPM,用多摩川的旋转变压器作为位置传感器,使用Magtrol 测功平台,电机采用表贴式永磁同步电机,具体参数为:额定转速nn=600 r/mim,额定转矩Tn=5 N·m,极对数pn=8,相电阻R=1.5 Ω,相电感L=2.65 mH,粘滞摩擦系数B=7.2e-4(N·m)/(rad·s-1),转子转动惯量J=1.4e-3 kg·m2,永磁磁链Ψf=0.1 Wb。
其中,相电阻R 和相电感L 是通过Agilent数字电桥E4980A 直接测得; 粘滞摩擦系数B和转子转动惯量J 是通过自由加减速法[10-11]实验测得;永磁磁链Ψf则是通过测出某一转速下电机的反电势再利用下式计算得出:

Magtrol 测功平台上的扭矩传感器TM306 可实时地输出与负载转矩成正比的电压信号,该信号经AD 采样后即可得到负载转矩TL。
实验结果如图2~图5所示。 从图2和图3可以看出,系统在启动和加载时刻q 轴电流均能很好地跟踪给定; 图4中电机转速能很好地跟踪给定转速,超调约为7%; 图5显示在系统加载时转速几乎没有跌落。 因此,基于反步控制器的永磁同步电机转速控制系统具有较好的转速、电流跟踪效果,并且具有较小的转速超调和极好的抗干扰性能。
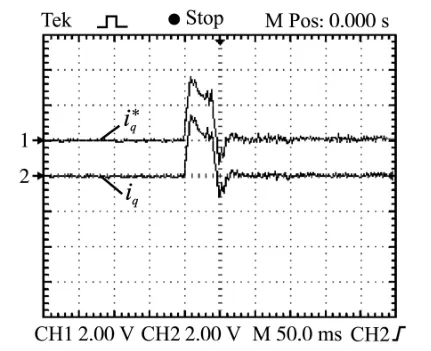
图2 启动时电流波形 (1.5 A/V) Fig.2 Current waveforms of starting (1.5 A/V)
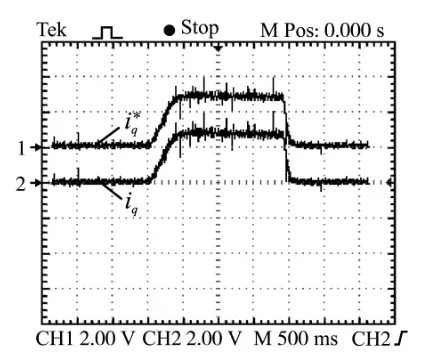
图3 加载时电流波形(1.5A/V)Fig.3 Current waveforms of load-on (1.5A/V)
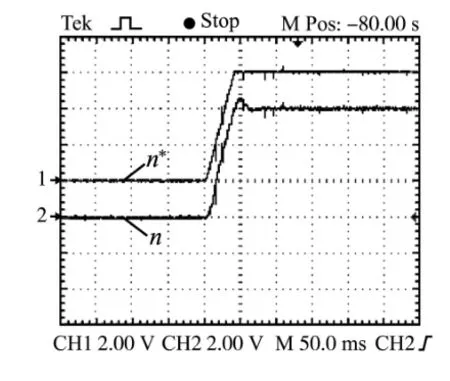
图4 启动时转速 (100 r·min-1/V) Fig.4 Speed waveforms of starting (100 r·min-1/V)
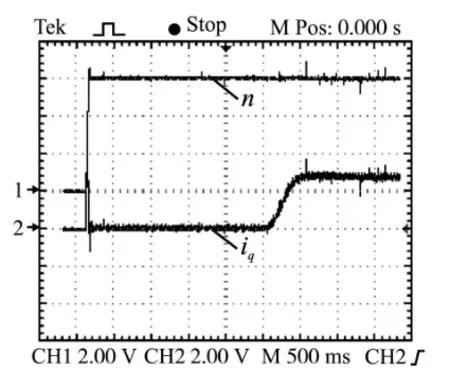
图5 系统启动与加载(n=100 r·min-1/V,iq=1.5 A/V)Fig.5 System starting and load-on(n=100 r·min-1/V,iq=1.5 A/V)
5 结论
文中针对永磁同步电机伺服系统的性能要求和结构非线性特点,利用反步方法设计出具有非线性特性的反步控制器。 相对于其它非线性控制器,该控制器结构简单、易于实现。 实验证明,基于反步控制器的永磁同步电机伺服系统具有优异的转速、 电流跟踪性能和抗干扰性能。 因此,反步设计方法在永磁同步电机伺服系统中具有较高的研究价值和实用价值。
[1] 陈伯时.电力拖动自动控制系统——运动控制系统[M].第3 版.北京:机械工业出版社,2003.
[2] 王家军,赵光宙,齐冬莲.反推式控制在永磁同步电动机速度跟踪控制中的应用[J].中国电机工程学报,2004,24(8):95-98.
[3] Dixon J,Tepper S,Moran L.Practical Evaluation of Different Modulation Technique for Current-controlled Voltage Source Inverters [J].IEE Proceedings on Electric Power Applications,1996,143(4):301-306.
[4] 胡强晖,胡勤丰.全局滑模控制在永磁同步电机位置伺服中的应用[J].中国电机工程学报,2011,31(18):61-66.
[5] 许强,贾正春,李朗如.带负载转矩补偿的PMSM 交流伺服系统自适应控制[J].电工技术学报,1997,12(5):1-4.
[6] 孙宜标.基于滑动模态的永磁直线同步电动机鲁棒速度控制[D].沈阳:沈阳工业大学,2007.
[7] Zhou J,Wang Y.Adaptive Backstepping Speed Controller Design for a Permanent Magnet Synchronous Motor [J].IEE Proceedings on Electric Power Applications,2002,149(2):165-172.
[8] Uddin M N,Lau J.Adaptive Backstepping Based Design of a Nonlinear Position Controller for an IPMSM Servo Drive[J].Canadian Journal of Electrical and Computer Engineering,2007,32(2):97-102.
[9] E Jean-Jacques,Li Weiping.Applied Nonlinear Control[M].Prentice Hall,New Jersey,1991.
[10] 才家刚.电机试验手册[M].北京:中国电力出版社,1997.
[11] 邱鑫.永磁交流伺服控制系统的动态性能研究 [D].南京:南京航空航天大学,2010.