直纹面叶片环形刀侧铣加工刀位规划的研究

王 波，刘献礼，岳彩旭

（1. 哈尔滨理工大学，哈尔滨 150040；2. 水力发电设备国家重点实验室，哈尔滨 150040；3. 哈尔滨电机厂有限责任公司，哈尔滨 150040）

前言

本文的研究对象为非可展直纹面叶轮叶片，非可展直纹面的特点是直母线上每点的法矢方向都不相同，这种特点将导致如果圆柱刀半径非零，则由它扫掠所生成的包络面不能与设计曲面完全相切，因此对于这种曲面的侧铣加工采用曲面逼近加工[1]。直纹面侧铣加工刀位主要的规划方法有两点偏置法、两点偏置优化法、三点偏置法，偏置的基本思想主要是通过提取直母线上的点，并对其进行半径距离偏置，从而得到相应位置的刀轴矢量。理论上在用半径大于零的圆柱刀对叶片包络滚动时会存在原理误差[2,3]。文献[4]研究指出：若给出已知曲面的实际参数与理论参数之间的误差区域，那么当进行等距偏置时（无主语）仍保持不变。因此，环形刀刀具包络面逼近设计曲面的问题就等价于刀轴轨迹面与设计曲面等距面的逼近问题。据此，后文计算叶片曲面的加工误差只需计算环形刀刀轴轨迹面上诸点至叶片曲面等距面的距离即可。

1 环形刀侧铣加工刀位优化

工程中直纹面是通过连接叶根线和叶顶线相对应的点来构成的，其中环形刀加工侧铣刀位变化如图 1所示。对初始刀位进行优化时，首先设Q( u)、W( u)为叶片的叶顶线与叶根线，在叶顶线的v方向等参线R(u)上选取刀位点Sn，再通过偏置得到偏置线的对应点，在逐点动态滑动时,点将作为滑移定点。与定点相对应的是滑移动点，动点Nn在叶跟线上逐点滑动，刀位优化过程中所遍历的点为 N1, N2,⋅ ⋅ ⋅Nk。首先确定定点'与初始动点N1，以初始刀位刀轴矢量作为滑动的初始位置，从第一个初始位置进行索引，第一个刀轴矢量为直母线所对应的偏置线T1，然后沿u方向进行逐点滑动索引，经过区间范围逐点搜索得到相应刀位点的刀轴矢量T2, T3, ⋅ ⋅ ⋅TK。优化过程如图2所示。

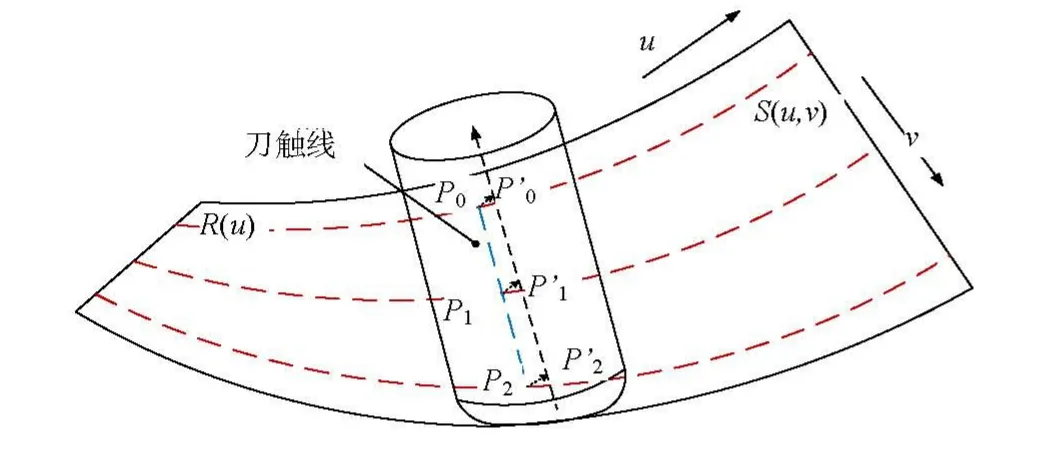
图1 环形刀初始刀位解析图

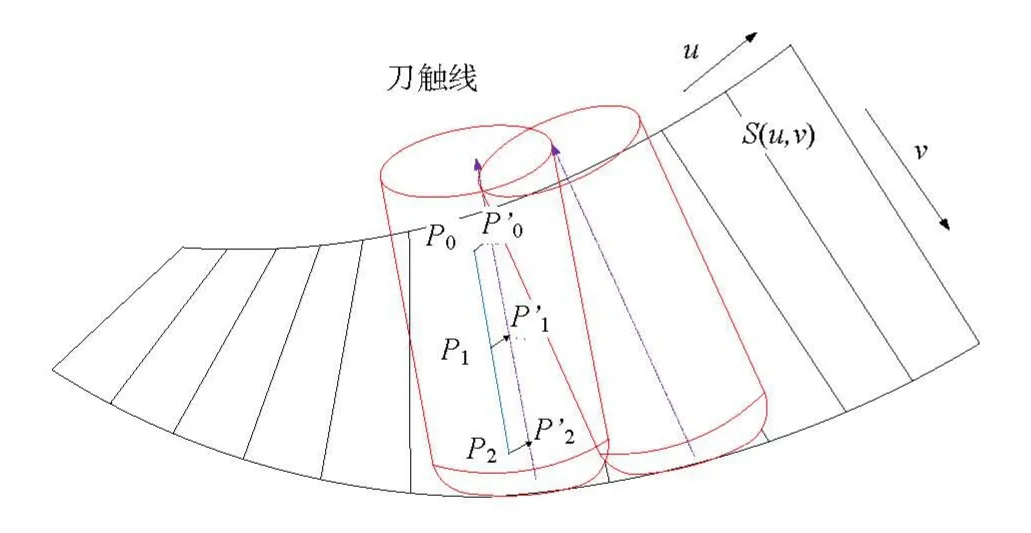
图2 环形刀侧铣刀位变化

运用此方法进行规划时，涉及到了非可展直纹面的划分问题。直纹面的细分实际上是选择一定点，并在定点周围选取一段长为定点到动点距离的区域，划分的原理可参照叶片等参数线的划分原则。此区域将随着动点变化而发生变化，将此区域在定点左右两侧各分为七段，当确定滑动方向后，只能对单侧进行划分。当对刀位进行动态滑动时，在各离散点位置计算所得的Lk值与新的刀轴矢量Tk变化范围如图3所示，图中动点实线表示未对初始刀位优化时的L值变化情况，虚线表示整个优化过程后L的变动范围情况，由图3可知，L呈抛物线形状变化，抛物线焦点刀轴矢量为'时，L达到最小值。

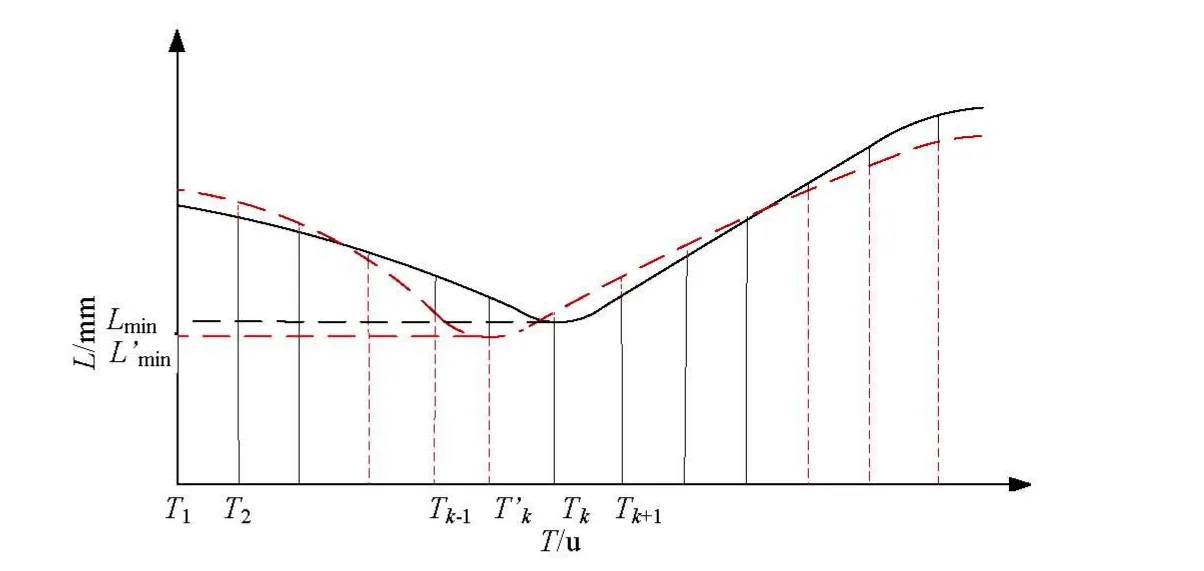
图3 误差极值对比分析

2 叶片加工误差的评价分析

若采用直径为 6mm的环形刀侧铣加工该不可展直纹面，针对文献提出的刀位算法与本文所规划的侧向偏置动态滑动法来进行误差对比计算，运用 UG软件中自带的偏差度量功能，所选对象为优化的刀轴轨迹面与设计曲面等距偏置面。应用上述方法生成无干涉的刀位轨迹，并输出几何误差。设计曲面上用曲面法向矢量表达该误差，通过使用 UG软件中自带的几何偏差分析功能，可以得到刀位优化前与优化后刀具包络面与设计曲面之间的几何极差分布图，如图4所示，可以发现在中间位置偏差最大，最大过切和欠切分别为 0.51mm和 0.70mm。优化后最大过切减小为0.1284mm，最大欠切为 0.1207mm。可以得出优化算法显著提高了加工精度。

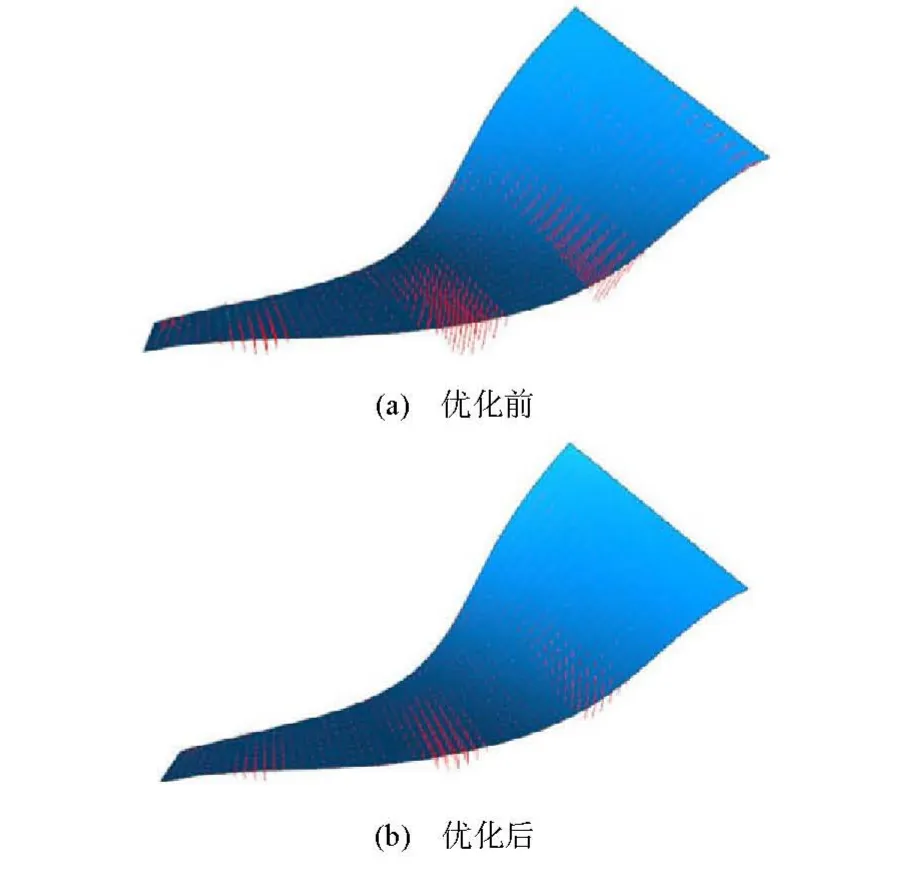
图4 叶片包络面与设计曲面极差对比分析

3 环形刀侧铣加工刀位轨迹生成

本文建立的刀位优化算法原理主要是将刀轴分别以叶顶定点、叶根动点在基线偏置线上进行滑动，确定滑动刀轴与叶片规划区间直母线间的最小值，然后基于走刀步长的确定原理，索引到动点刀位误差最小的矢量方向，此处就为所求的优化刀轴矢量。这种方法考虑到整体刀位的规划，具有局部整体性，对于不可展直纹面来说，可有效降低其过切，并保证优化刀轴方向不与相邻叶片发生干涉。图5分别给出了环形刀侧铣加工非可展直纹面每一刀位刀轴矢量的变化情况，从刀轴矢量变化情况观察，可以发现在优化前无论在叶根部还是叶顶部刀轴矢量变化幅度较大，不能保证侧铣刀具与直纹面的切触线误差在合理的范围内，加工质量较差。优化后的刀轴变化较均匀，与驱动曲面接触充分，可满足刀具包络面与设计曲面在合理误差范围内。

图5 叶片侧铣刀位刀轴矢量对比

4 结论

（1）在刀位优化推导过程中，建立了刀轴侧向偏置滑动算法。分别从初始刀位的U向离散点优化与侧向偏置滑动刀轴最小误差评价两方面进行计算，并且引入比例因子，简化了刀位算法计算量，提高了编程效率。

（2）根据本文所建立的刀位算法原理，得到了有效的走刀步长计算方法，并将刀位计算结果应用到编程软件中，验证了刀位算法的正确性。

（3）本文所建立的环形刀刀位优化算法，干涉误差计算结果较好，与文献[5]提出的基于动力学优化方法相比，误差极值降低，有效地提高了环形刀加工非可展直纹面的精度。

[1]苏云玲. 三元整体叶轮的几何造型五坐标数控加工[D]. 大连理工大学, 2004.

[2]何道贵. 透平叶轮数控加工[J]. 计算机辅助设计与制造, 2000, 2(3): 11-14.

[3]Zhu L M,Zheng G, Ding H. Formulating the swept envelope of rotary cutter undergoing general spatial motion for multi-axis NC machining[J]. Int J Mach Tool Manu, 2009, 49(2): 199-202.

[4]FAN J, BALL A. Quadric method for cutter orientation in five-axis sculptured surface machining[J]. International Journal of Machine Tools& Manufacture, 2008, 48(7-8): 788-801.

[5]Senatore J, Monies F, Redonnet J M, et al.Improved positioning for side milling of ruled surfaces:Analysis of the rotation axis's influence on machining error[J]. International Journal of Machine Tools and Manufacture, 2007, 47: 934-945.