一类食物链模型Hopf分支的存在性
张 玲,郭 爽
(大庆师范学院数学科学学院,黑龙江大庆163712)
□数 学
一类食物链模型Hopf分支的存在性
张 玲,郭 爽
(大庆师范学院数学科学学院,黑龙江大庆163712)
考虑了一类三维Gause型食物链模型,通过对模型线性部分对应特征方程特征根的分布情况的讨论给出了共存平衡解的稳定性和Hopf分支的存在性,并给出了一组数值模拟数据来说明分支周期解的方向,周期及其稳定性。
Gause型食物链;Hopf分支;数值模拟
0 引言
在自然界中,生物种群的关系会随着种类的增加而变得更加复杂。例如三个种群之间有可能是捕食与被捕食形式,有可能是竞争或者共存关系,也有可能表现为食物链形式。
Freedman等[1]提出了一类Gause型食物链模型:

这里x,y,z分别是食饵,捕食者和顶层捕食者的密度,g(x)为食饵x的相对增长率。p(x),q(y)分别为捕食者和顶层捕食者得功能反应函数,h,e,s,m>0分别对应着死亡率,以及食饵和捕食者的转化率。许多作者对该模型进行了详细的研究[2-4]。
为了理解种群密度的震荡现象,引入一个单一时滞到模型的功能反应函数中是最好的方法,如文献[5-7]。我们这篇文章的主要目的是把时滞引入到顶层捕食者的功能反应函数中,分析该模型所出现的分支现象。
1 共存平衡点的稳定性分析

这里非量纲化处理不会改变平衡点的性质,经过简单的计算,我们知道(2)有四个平衡点:E1(0,0,0),E2(1,0,0),E3(x0,y0,0)及E*(x*,y*,z*)。其中

E1(0,0,0),E2(1,0,0)和E3(x0,y0,0)标志着种群数量会有不同程度的灭绝,我们主要研究共存平衡点E*(x*,y*,z*)随着时滞的增加会产生怎样的变化。
考虑E*(x*,y*,z*)处的线性化系统,其雅克比行列式为:

其特征方程为

其中a2=-m11,a1=-m12m21,b1=-m23n32和b0=m11m23m32。
如果m11<0,那么当τ=0时,根据Routh-Hurwitz准则,(3)的所有特征根都具有负实部,于是有以下引理:
引理:如果m11<0,方程(2)的共存平衡点E*(x*,y*,z*)是局部渐近稳定的。
当τ≠0,把λ=iω代入(3),有:
1)当ω=0,D(0,τ)=m23n23m11≠0;
2)当ω≠0,D(iω,τ)=(iω)3+a2(iω)2+a1iω+(b1iω+b0)e-iωτ=0
分离实虚部,有

平方相加,有

令ω2=l,则方程(5)变成

由于h(0=-b20<0,而且lli=m∞h(l),根据[8],(6)至少存在一个正根,不失一般性,我们假设(6)有三个正根,记为l1,l2和l3,相应的(5)有三个正根,分别为.根据(4)有

k=1,2,3;j=1,2,……,所以(±ωk,τjk)是(3)的解。
定义:
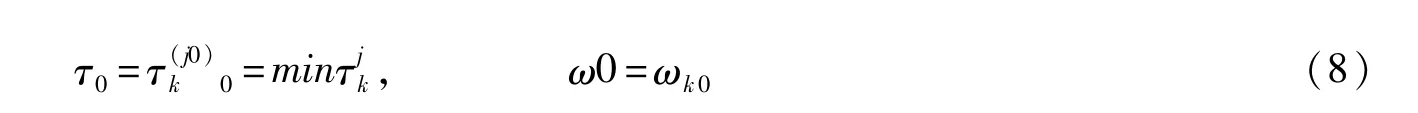
即±ω0是τ=τ0时(3)的纯虚特征根,于是下面定理成立:
定理:τ0和ω0如(8)定义,系统(2)的共存平衡点E*(x*,y*,z*)在τ∈[0,τ0]上是渐近稳定的。此外,若h′(w。)≠0,那么当τ=0时,(2)于E*(x*,y*,z*)处经历Hopf分支。
证明:由于h(0)=-b20<0,知(3)必存在纯虚特征根,由文献[8]定理的前半部分成立。我们只需证明当τ=τ0时,Hopf分支存在的横截条件成立。假设

所以

2 数值分析
由文献[6]知在中心流形上分支周期解的方向,周期和稳定性由下式描述

下面给出计算机得到的一组数据,我们选择a=2.712,b=0.223,c=0.765,r=0.811,s=0.771,d=0.01,l=0.115,经过复杂的计算,我们得到:平衡点为E*(0.642,0.712,0.375),其他的重要参数值为c1=-17.472-20.974i,μ2=2.9017,T2=5.4141β2=-1.9017。由文献[6]的中心流形和规范型理论知(2)的Hopf分支是上临界的,分支周期解是稳定的,分支周期解的周期是增加的。
[1]Freedman H.I.,Waltman P..Mathematic analysis of some three species food chain models[J].Math.Biosci.,1978,33:257-276.
[2]Wonlyul Ko,Kimun Ryu.A qualitative study on general Gause-type predator-preymodelswith non-monotonic functional response[J].Nonlinear Analysis:RealWorld Applications,2009(10):2558-2573.
[3]S.M.Moghadas,B.D.Corbett.Limit cycles in a generalized Gause-type predator-preymodel,Chaos[J].Solitons and Fractals2008,37:1343-1355.
[4]Wonlyul Ko,Kimun Ryu.A qualitative study on general Gause-type predator-preymodelswith constant diffusion rates[J].J.Math.Anal.Appl,2008,34(4):217-230.
[5]Xiaoquan Ding,Jifa Jiang.Multiple periodic solutions in generalized Gause-type predator-prey systemswith non-monotonic numerical responses[J].Nonlinear Analysis:RealWorld Applications,2009(10):2819-2827.
[6]Hassard B D,KazsinoffW D,Wan Y H.Theory and Application of Hopf bifurcation[M].London:Cambridge University Fress,1982:14-70.
[7]H.B.Wang and W.H.Jiang.Hopf-pitchfork bifurcation in van der Pol's oscillatorwith nonlinear delayed feedback[J].Journal of Mathematical Analysis Applications,2010,36(2):9-18.
[8]S.G.Ruan,J.J.Wei.On the zeros of a third degree exponential polynomialwith applications to a delayedmodel for the control of testosterone secretion[J].Mathematical Medicine and Biology,2001,18(1):41-52.
Hopf Bifurcation Existence on Aood Chain M odel
ZHANG Ling,GUO Shuang
(College of Mathematics Science,Daqing Normal University,Daqing 163712,China)
A class of3-dimensional Gause food chainmodel is considered.The stability of the equilibrium points and the existence of Hopf bifurcation are obtained via employing the polynomial theorem to analyze the distribution of the roots of the associated characteristic equation with the linear partof themodel.A numerical simulation is carried out to illustrate the results.
Gause food chain model;Hopf bifurcation;numerical simulations.
张玲(1978-),女,黑龙江大庆人,大庆师范学院数学科学学院讲师,博士生,从事随机微分方程数值解研究。
黑龙江省教育厅科学技术研究资助项目(12523001)。
TN911.8
A
2095-0063(2013)06-0048-04
2012-11-20

