微分中值定理教学中的几种辅助函数的构造

周寿明

(重庆师范大学 数学学院，重庆 401331)

辅助函数的构造在很多问题的解决中都起着关键的作用，因此它的作用非常之广泛。几乎所有数学专业的教材中都要用到辅助函数去解题，但都只是作为一种数学工具被“信手拈来”，让初学者连看都感到困惑更不用说去掌握和运用它。本文通过对例题进行归纳、分析和总结出常见的五种构造辅助函数的方法——行列式法、变上限积分法、微分方程法、常值K 法、指数因子法。本文旨在找出这些辅助函数特点及适用对象，根据题意合理构造出辅助函数，使解题思路更加清晰、解题过程更加明了。并由此得出利用辅助函数解题的一般步骤。

1 行列式法

数学的各门学科之间是普遍联系的。借助高等代数中的行列式来构造辅助函数，有时可以使问题变得更加直观、明了。

行列式的微分性质［1］设fij(x)(i，j = 1，2，…)为可导的函数，则有

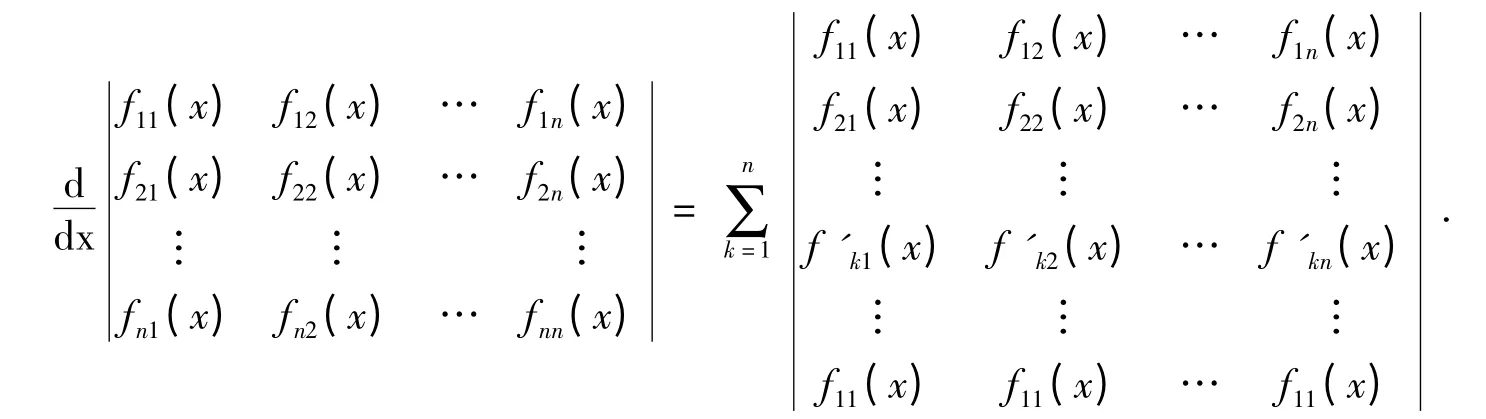
［例1］设f(x)，g(x)，h(x)在a ≤x ≤b 上连续，在a ＜x ＜b 内可导，证明:必存在一点ξ ∈(a，b)使

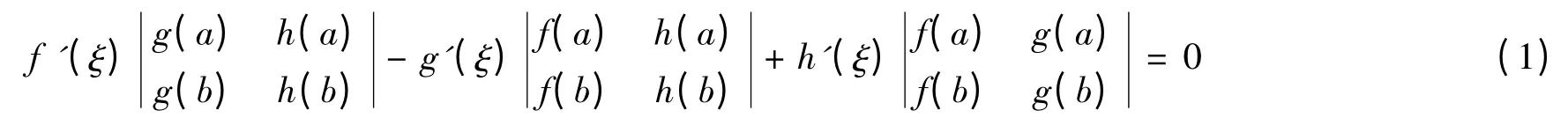
证明:该题要证的结论中出现了行列式，易知此题应构造如下一个行列式作为辅助函数:

由于F(a)= F(b)= 0 ，由题设知F(x)满足罗尔定理的条件，故至少存在一点ξ ∈(a，b)使

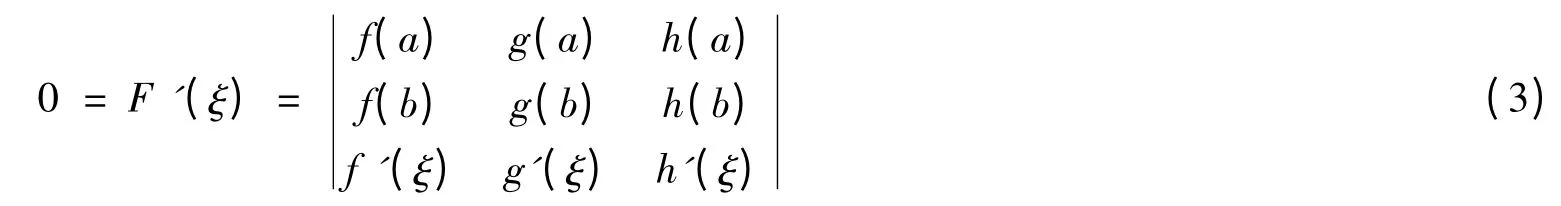
将(3)式按最后一行展开即可得(1)式。证毕。

事实上，拉格朗日中值定理和柯西定理都是(3)式的特例，亦即由此可得到这两大定理的另一种证明方法:若令h(x)= 1 ，由(3)式即得柯西中值定理;若令h(x)= 1 ，g(x)= x，即得拉格朗日中值定理。

2 变限积分法

变限积分是证明积分等式、不等式的一种非常重要且行之有效的方法。主要是因为这类积分的函数具有很好的微分性质。

积分法的微分性质［1］设f 为连续函数，u，v 均为可导函数，且可实行复合与。则有:

在x ∈［a，b］上φ(x)单调递减，又因为φ(a)= 0 ，故。证毕。

3 微分方程法

当所要证明的结论中代数式比较复杂时，就不能很容易通过变限积分法找出原函数，这时我们通过微分方程的方法解决［2］。

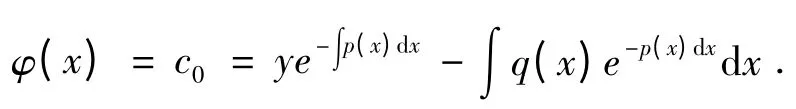
［例3］设f(x)在闭区间［0，π］上连续，在开区间(0，π)内可导，且f(x)= 0 ，求证:至少存在一点ξ ∈(0，π)，使得

4 常值K 法

常值K 法的一般步骤［3］:1)将结论中的所有常数分离至等式的一端，并设其为常数K;2)将所得等式进行恒等变形，使含a 和f(a)的都移到等式的一端，另一端含b 和f(b);3)判断上式是否为对称式，若对称则将a 变成x，将f(a)变成f(x)，即得到所需的辅助函数。

［例4］设设函数f(x)在闭区间［a，b］上连续，在开区间(a，b)内可导，求证:至少存在一点ξ ∈(a，b)使得:bf(b)－af(a)=(b－a)f(ξ)+ ξf '(ξ).

5 指数因子法

由指数函数ex的各阶导数仍然是ex，并且ex恒大于零，我们可以利用指数函数ex的这种良好性质构造ef(x)型辅助函数［4］。

［例5］设f(x)在［a，b］连续且有连续的导函数，若f(0)= f(a)，求证:至少存在一点ξ ∈(0，a)，使得:f'(ξ)= 3ξ2(f(ξ)－f(0))。

众所周知，辅助函数的构造有很大的灵活性和技巧性，应就具体问题具体分析，充分挖掘已知条件和所证结论中蕴涵的信息，大胆地运用归纳、猜想、分析与化归等数学思想，选择合适的辅助函数，最终解决问题。因此，我们要对辅助函数的性质、特征非常的熟悉，对它们的使用范围“了如指掌”，平时多做题、多思考、多总结，只有这样才能合适的选择、灵活地运用辅助函数进行解题。

［1］华东师范大学数学系. 数学分析［M］. 北京:高等教育出版社，2001.

［2］王文珍. 微积分学中辅助函数的应用［J］. 长江大学信息与数学学院，2005，8(6):33－35.

［3］朱崇军，徐侃. 微分中值定理应用中辅助函数的构造［J］. 高等函授学报，2008，22(1):18－20.

［4］谭洁琦. 浅谈微分中值定理证明中辅助函数的构造［J］. 四川教育学院学报，2008，24(7):101－103.