一种模糊时态描述逻辑

冉 婕，黄吉亚，高 琴

（云南昭通学院 信息科学与技术学院，云南 昭通 657000）

描述逻辑是一类知识表示的形式系统，通过定义应用领域的概念及其结构关系，刻画领域内的个体信息[1]。描述逻辑吸收了KL-ONE的主要思想，是一阶逻辑的可判定子集，基于其推理机制的有效性，它目前已成为国内外研究的热点。经典的描述逻辑虽然能很好地处理精确信息，但不具备处理模糊信息的能力，Stracci将模糊集合论引入描述逻辑，扩展描述逻辑ALC提出了模糊的ALC（FALC）[2]，FALC是描述逻辑的模糊化推广，它结合了模糊逻辑与描述逻辑的特性，给出了基于约束传播的推理算法，并证明了FALC推理问题的复杂性，FALC为新一代的描述逻辑提供了处理模糊概念的应用基础。时态逻辑是非经典逻辑的分支学科，时态扩展可以看作是模态扩展的一种特殊形式。在描述逻辑中第一个整合时间的方法是由A.Schmiedel提出来的，他使用了两个时间运算符来扩展描述逻辑，提出了在时间段上受限的全称和存在量词[3]。常亮等提出了可判定的时序动态描述逻辑[4]。孙永新等提出了描述逻辑的动态时序扩展[5]。

1 模糊时态描述逻辑

模糊逻辑从研究模糊性出发，把元素属于集合的观念模糊化，承认论域上存在既非完全不属于某集合，又非完全属于某集合的元素，将属于概念量化，承认论域上的不同元素对同一集合有不同的隶属度。在现实生活中，许多的信息具有时间属性，比如，命题“未来几天小雨转多云”，在这个命题中，“未来几天”是个时间属性，“多云”具有模糊性。在模糊逻辑中加入时态算子具有一定的研究意义。昌霞等在研究已有的模糊逻辑的基础上，增加时态算子□（过去的任一时刻），◇（过去的某一时刻）和○（下一时刻），提出了一种时态模糊描述逻辑[6]，但3个时态算子表达较简单，不能描述具体时间段的模糊命题。本文根据时间的特性，用区间来刻画时间区域，同时用另一不同的区间来刻画概念的隶属度，提出了一种新的模糊时态描述逻辑——FTDL。

1.1 模糊集

模糊集合理论概念是由美国控制论专家L.A.Zadeh在1965年提出来的。模糊集合着眼于现实世界的不精确和不完整的信息传感，以隶属度作为建立基石，通过定义的隶属度特征函数表达模糊性。隶属函数将经典的二值逻辑{0，1}扩充为[0，1]区间内的连续值逻辑。隶属函数具有离散和连续两种形式，常见的有三角形隶属函数、模型隶属函数、高斯函数形隶属函数、柯西函数形隶属函数等。本文对个体，概念和关系的模糊隶属度是用vague集来描述，即对论域上的某个元素u将其隶属度函数限定到[0，1]的子区间[tv（u），1-fv（u）]上，将隶属函数值用区间来表示，并不讨论某一具体的隶属函数。

1.2语 法

模糊时态描述逻辑FTDL的语法是模糊描述逻辑ALCN的语法的扩充。本文在此定义CFN，RFN，IFN分别为FTDL的概念名集合，关系名集合和个体名集合。

定义2.1在T－FALC中，概念定义如下：

1）原子概念A、全概念┬、和空概念 都是概念；

2）如果C和D是概念，则┐C，C∩D，C∪D都是概念；

3）如果R是关系，C为概念∃R.C，则，∀R.C也是概念；定义2.2 在FTDL中，对关系定义为：

1）原子关系P是关系；

2）如果R是关系，┐R也是关系。

定义2.3 在整个时间轴上T（x）＝{ti|－∞＜ti＜∞|}，可以在某个点上进行概念的描述，也可以在某个区间上进行概念的描述，本文中刻画概念所满足的时间区间所用的是[ti，tj]，其中－∞＜ti＜tj＜∞，当ti＝tj时，时间区间将退化成某个时间点。

定义2.4 在FTDL中对于隶属度刻画，用α，α1，α2，…来表示隶属区间的下限，用β，β1，β2，…来表示隶属区间的上限。例如[α，β]，其中；0≤α≤β≤1；[α3，β3]，其中0≤α3≤β3≤1，都表示为具体的隶属区间。

定义2.5设a，b，…表示个体实例，FTDL的ABox AB由下列事实断言组成：

1）断 言 公 式：形 如C[ti，tj][α，β]（a），R[ti，tj][α，β]（a，b）的 表 达 式；公 式 上标代表的是时间区间，下标代表的是概念隶属度区间，C为概念，R为关系，称这样的公式为断言公式。

2）个体公式：形如，a＝b，a≠b。

定义2.6 FTDL的TBox TB由下列术语公理组成：

1）概念模糊包含：称概念D模糊包含概念C当且仅当对所有解释I都有CI⊆FDI成立，记作：C⊆FD；

2）概念模糊相等：称概念C，D是模糊等价的当且仅当C，D互模糊包含，即：C⊆FD，D⊆FC，记作：C≡FD；

3）概念不相交：称概念C，D不相交当且仅当C，D的交集为空，记作：C∩D＝Ø。

定义2.7 FTDL的知识库KB＝＜FAB，FTB＞，其中FAB为FTDL的ABox，FTB为FTDL的TBox。

例如，FavouriteMovie[ti，tj][0.6，0.8]（Ghost）表达的是“人鬼情末 了”这部影片在某段时间是较受欢迎的电影，Cooperate[ti，tj][0.1，0.2]（a，b）则说明个体a和b在某段时间内合作关系的可能性较低。

1.3 语义

FTDL的语义模型用一个二元组K＝（Δ，I）来表示：

1）非空集合Δ是FTDL中所有个体对象的集合，又叫做论域；

2）对FTDL中的个体，概念和关系加以解释的映射I。

模糊描述逻辑中的语义是将概念解释为一定论域的模糊子集，关系是该论域上的模糊二元关系。本文中应用的是综合vague模糊解释和时态解释的模糊时态解释I＝（ΔI，·I），其中，解释论域ΔI是非空的个体集合，·I是解释函数。 其中解释函数·I是将概念解释为论域ΔI的模糊子集，关系是该论域上的模糊二元关系。本文中的解释，给予以下定义：

定义2.8对于模糊时态描述逻辑FTDL中的解释I＝（ΔI，·I），其中解释函数为·I，解释论域为ΔI，对于解释函数·I需满足如下几点：

1）对于任意个体a和b，如果a≠b，则aI≠bI；

2）对于任意概念C，解释函数·I将C映射为一个隶属函数：CI：ΔI→{＜[ti，tj]，[α，β]＞|ti≤tj，0≤α≤β≤1}；其 中＜[ti，tj]，[α，β]＞这样的二元组中[ti，tj]表示时间区间（公式的上标），[α，β]表示隶属区间（公式的下标）。

3）对于任意关系R，解释函数·I将R映射为一个隶属函数RI：ΔI×ΔI→{＜[ti，tj]，[α，β]＞|ti≤tj，0≤α≤β≤1}。

其中，α和β分别是从vague集的真隶属函数tv和假隶属函数fv中得到的隶属度。概念C的解释CI是在某个时间区间里相对于I的概念集C的隶属函数，例如d∈ΔI，则CI（d）表示在解释I下个体d在某时间区间内属于模糊概念C的程度。

假设给定模糊概念C，D，用tCi，tDi分别表示C和D时间区间的下限，tCj，tDj分别表示C和D的时间区间的上限；而αCI（d），αDI（d）分别表示个体d属于模糊概念C和D的隶属度区间的下限，βCI（d），βDI（d）分别表示的是个体d属于C和D的隶属区间的上限。依此类推，αRI（d，d′）表示个体d，d′满足模糊关系R的隶属 区间下限，βRI（d，d′）表示个体d，d′满足R的隶 属 区间上限，tid，tjd分别表示个体d满足模糊关系R的时间区间上限和下限，tid′，tjd′分别表示个体d′属于模糊概念C的时间区间上限和下限。

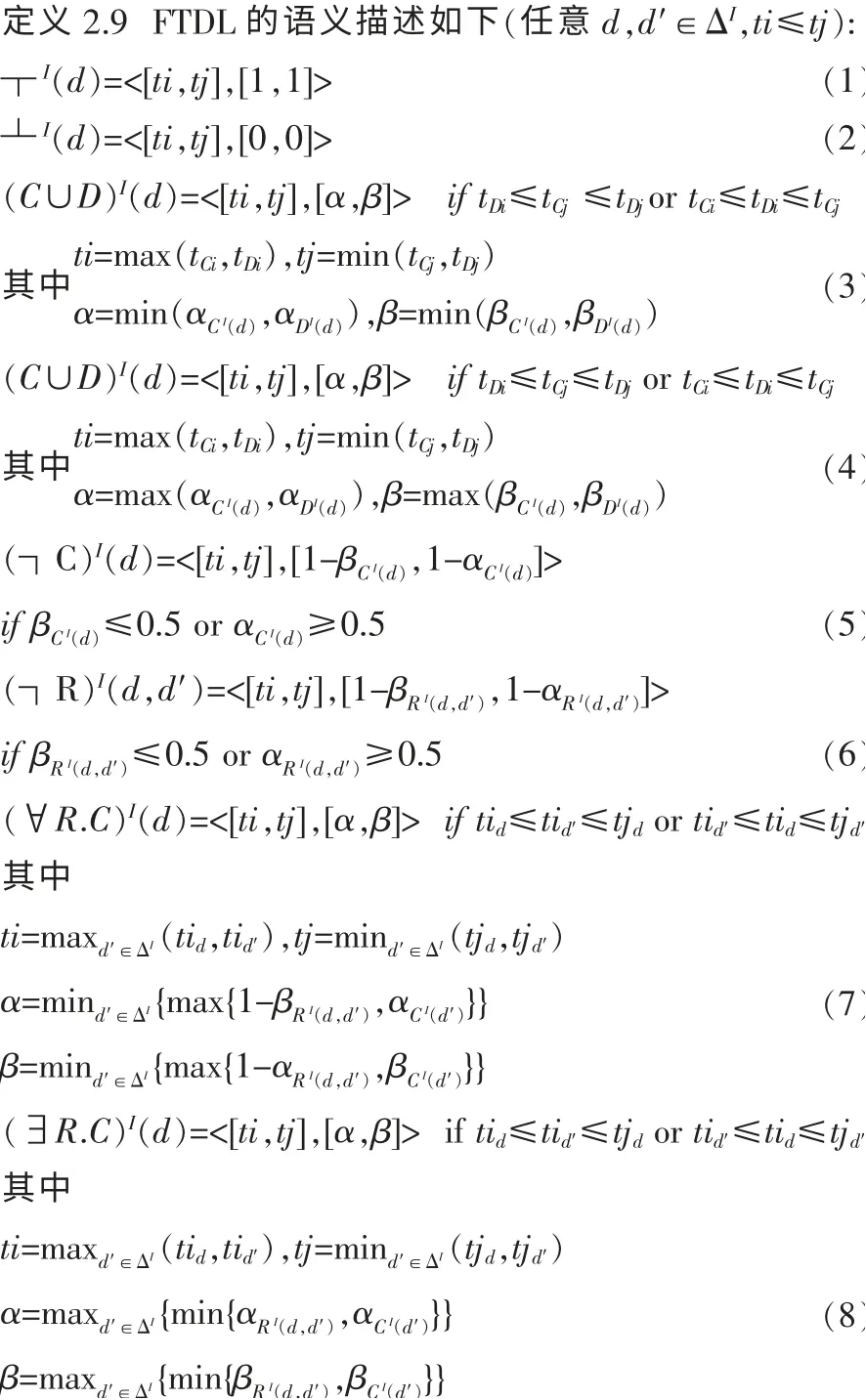
说明：上述（3），（4）式是对概念作析取，合取操作，对于时间上要求两个概念的时间区间有交集，即[tCi，tCj]∩[tDi，tDj]≠Ø。式（5），（6）都是作否定操作，在此就（5）式而言，仅只讨论αC≥0.5 orβC≤0.5时的情况，即概念C的隶属区间要么较小，要么较大，对于中间区间，比如[0.4，0.6]，本文认为其概念已包含其否定含义，在此不作讨论。对于∀R.C和∃R.C利用的是模糊理论里的极大极小复合运算原则，也可以转化为一阶逻辑公式。全称量词表示论域元素上的合取，如（7）式用的就是F∀R.C（x）＝∀y.┐FR（x，y）∨FC（y）；存在量词∃表示论域元素上的析取，对于（8）式用到的是F∃R.C（x）＝∃y.FR（x，y）∧FC（y）。对于（7）和（8）式本文依然是要求其时间区间有交集，即[tid，tjd]∩[tid′，tjd′]≠Ø。

2 简单实例

关于天气预报，涉及到的影响因素较多，在此例中，仅讨论四种天气情况，分别为晴（sun），雨（rain），阴（cloudy），雪（snow），其中雨天又细分为阵雨（shower），大雨（downfall）和冰雨（sleet）三种情况；影响天气的因素在这里给出如下几种：云（cloud），风（wind），雾（fog），雷 电（thurder），阳 光（sunshine），降雨量（rainfall）；在T＝{…t1，t2，t3，…tn，tn+1…}上，假设有－∞＜th＜ti≤tj＜tk＜∞，则[ti，tj]⊂[th，tk]。下面给出基于天气预报示例的的知识库KB＝{FAB，FTB}，FAB为其断言公式集合，FTB为其术语公理集合。对于知识库的构建初始化为：

通过推导，可得北京昨天有降雨的概率为[0.3，0.5]，还可推导出上海明天为阴天的概率是[0.3，0.4]，而且根据已经断言可以推导西安明天24小时为晴天的概率是[0.3，0.5]。

3 结束语

本文分析了描述逻辑的研究现状，针对现实生活中信息的时间性和模糊性，在模糊描述逻辑和时态逻辑的基础上，提出了一种新的描述逻辑，即模糊时态描述逻辑，并在此基础上给出了其语法和语义的相关说明。下一步的工作将完善模糊时态描述逻辑的推理机制，包括断言公式集的一致性推理以及可满足性推理算法。

[1]Baader F，Nutt W.The Description Logic Handbook：Theory，Implementation and Applications[M].Cambridge：Cambridge University Press，2003.

[2]Straccia U.Reasoning within fuzzy logics[J].Journal of Artificial Intelligence Research，2001，14（1）：137－166.

[3]Albrecht Schmiedel.A temporal terminological logic[C]//Proc of the 8th Nat Conf on Artificial Intelligence（AAA I'90）.Boston，MA：M IT Press，1990：640－645.

[4]CHANG Liang，SHI Zhong-zhi，CHEN Li-min，et al.Family of extended dynamic description logics[J].Journal of Software，2011，22（7）：1525－1537.

[5]SUN Yong-xin，ZHAO Xi-shun，FU Zhi-qiang.Dynamic linear temporal extensions of description logics[J].Application Research of Computers，2012，29（2）：536－541.

[6]CHANG Xia，SUN Yu，RAN Jie，et al.A new logic of temporal fuzzy attribute language complement[J].Microcomputer&Its Applications，2010，29（302）：75－77.